

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Случайная величина 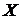 , принимающая целые значения от 0 до
, принимающая целые значения от 0 до 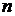 , имеет биномиальное распределение, если
, имеет биномиальное распределение, если
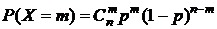 .
.
Такое распределение имеет случайная величина 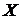 , равная числу осуществлений некоторого события А в серии из
, равная числу осуществлений некоторого события А в серии из 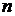 испытаний, в каждом из которых вероятность появления события А постоянна и равна
испытаний, в каждом из которых вероятность появления события А постоянна и равна 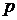 . Числовые характеристики биномиального распределения можно найти по формулам:
. Числовые характеристики биномиального распределения можно найти по формулам:
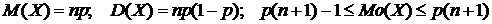 .
.
Пример. В корзине 50 шаров, из них 10 черных. Достают 5 шаров, причем выборка осуществляется с возвращением. Охарактеризовать случайную величину Х — число обнаруженных в выборке шаров черного цвета.
Величина Х может принимать значения от 0 до 5, т. к. выборка проводится с возвращением, вероятность 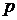 обнаружить всякий раз черный шар постоянна и равна 10/50 = 0,2. Вероятности каждого значения
обнаружить всякий раз черный шар постоянна и равна 10/50 = 0,2. Вероятности каждого значения 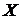 вычислим по формуле Бернулли:
вычислим по формуле Бернулли:
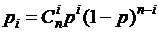 , где
, где 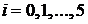 .
.
Получим ряд распределения:
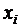
| ||||||
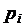
| 0,32768 | 0,4096 | 0,2048 | 0,0512 | 0,0064 | 0,00032 |
Найдем функцию распределения 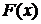 :
:
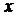
| 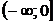
| 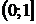
| 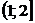
| 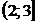
| 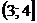
| 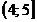
| 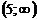
|
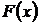
| 0,32768 | 0,73728 | 0,94208 | 0,99328 | 0,99968 |
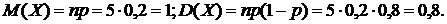
Наивероятнейшее значение 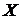 (
(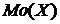 ) определяется из неравенства
) определяется из неравенства
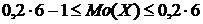 или
или 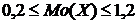 .
.
Целым значением, удовлетворяющим этим двум неравенствам, является 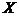 = 1. Значит,
= 1. Значит, 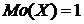 , что видно и из ряда распределения.
, что видно и из ряда распределения.
Гипергеометрическое распределение ДСВ
Случайная величина Х имеет гипергеометрическое распределение, если
 .
.
Такое распределение получается в следующей задаче. Имеется генеральная совокупность из  объектов, в числе которых находится
объектов, в числе которых находится  интересующих исследователей объектов. Из генеральной совокупности проводится выборка без возвращения объемом
интересующих исследователей объектов. Из генеральной совокупности проводится выборка без возвращения объемом 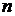 . Тогда случайная величина
. Тогда случайная величина 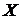 , равная числу интересующих нас объектов из совокупности
, равная числу интересующих нас объектов из совокупности  , обнаруженных в выборке, имеет гипергеометрическое распределение.
, обнаруженных в выборке, имеет гипергеометрическое распределение.
|
|
Пример. Воспользуемся условием предыдущей задачи, считая, что выборка осуществляется без возвращения, и найдем закон распределения случайной величины 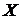 , равной числу черных шаров в выборке.
, равной числу черных шаров в выборке.
Случайная величина 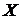 может также меняться от 0 до 5. Вычислим вероятности каждого значения по формуле:
может также меняться от 0 до 5. Вычислим вероятности каждого значения по формуле:
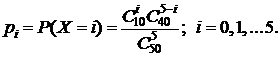
Составим ряд распределения

| ||||||

| 0,310563 | 0,431337 | 0,20984 | 0,044177 | 0,003965 | 0,000119 |
Как видим, вероятности отдельных значений Х несколько изменились по сравнению с их значениями, рассчитанными по формуле Бернулли.
Числовые характеристики гипергеометрического распределения:

В данном примере  .
.
Формулой для математического ожидания можно воспользоваться для оценки размера генеральной совокупности, если непосредственно подсчитать число объектов в ней затруднительно. Такая ситуация возникает, если нужно знать, например, число животных в популяции, обитающей на какой-либо территории, число птиц в стае, рыб в замкнутом водоеме и т. п. В этом случае метят  объектов из всей совокупности. Через некоторое время отбирают
объектов из всей совокупности. Через некоторое время отбирают 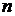 объектов и записывают количество меченых. Повторяя отбор несколько раз, находят среднее количество меченых объектов, которое можно принять равным
объектов и записывают количество меченых. Повторяя отбор несколько раз, находят среднее количество меченых объектов, которое можно принять равным  . Зная
. Зная 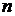 ,
,  и
и  можно найти
можно найти  .
.
|
|
|

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!