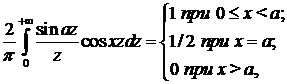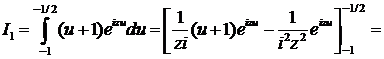Показательная и тригонометрические функции комплексного переменного z определяются равенствами, верными для любого z:


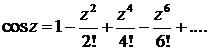
Эти ряды сходятся во всей комплексной плоскости.
Между указанными функциями существуют следующие соотношения:
 (1)
(1)
 (2)
(2)
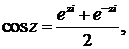 (3)
(3)
 (4)
(4)
называемые формулами Эйлера.
Cпомощью формулы (1) комплексное число, заданное в тригонометрической форме  может быть представлено в показательной форме
может быть представлено в показательной форме 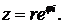
475. Представить в тригонометрической и показательной формах комплексное число 
∆ Находим 
 Следовательно, тригонометрическая форма данного числа имеет вид
Следовательно, тригонометрическая форма данного числа имеет вид  а показательная форма—вид
а показательная форма—вид  ▲
▲
476. Представить в показательной форме число 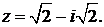
∆ Имеем 
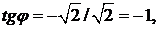
 т. е.
т. е.  ▲
▲
477. Записать в алгебраической форме 
∆ Воспользуемся формулой (1):

478. С помощью формулы Эйлера доказать, что

∆ Так как  то
то

 ▲
▲
479. Представить в показательной форме число 
480. Представить в показательной форме число 
481. Записать в алгебраической форме 
482. Показать, что 
483. Выразить  линейно через
линейно через  и
и  .
.
484. С помощью формулы Эйлера показать, что  имеет бесчисленное множество значений, которые все являются действительными.
имеет бесчисленное множество значений, которые все являются действительными.
РЯД ФУРЬЕ
Рядом Фурье периодической функции f(х) с периодом 2π, определенной на сегменте  называется ряд
называется ряд
 (1)
(1)
где
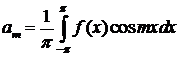 ,
, 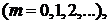
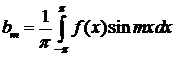 ,
, 
Если ряд (1) сходится, то его сумма S (х) есть периодическая функция с периодом 2π, т. е. 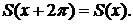
Теорема Дирихле. Пусть функция f(х) на сегменте  имеет конечное число экстремумов и является непрерывной ва исключением конечного числа точек разрыва I рода (т. е. удовлетворяет так называемым условиям Дирихле). Тогда ряд Фурье этой функции сходится в каждой точке сегмента
имеет конечное число экстремумов и является непрерывной ва исключением конечного числа точек разрыва I рода (т. е. удовлетворяет так называемым условиям Дирихле). Тогда ряд Фурье этой функции сходится в каждой точке сегмента  и сумма S (х) этого ряда:
и сумма S (х) этого ряда:
1) S (x) = f(x) во всех точках непрерывности функции f(х), лежащих внутри сегмента 
2) 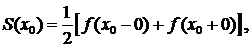 где x0—точка разрыва I рода функции f(х);
где x0—точка разрыва I рода функции f(х);
3) 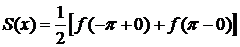 на концах промежутка, т.е. при
на концах промежутка, т.е. при 
Если функция f(х) задана на сегменте  , где l —произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье
, где l —произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье

где


В случае, когда f(x) — четная функция, ее ряд Фурье содержит только свободный член и косинусы, т. е.

где
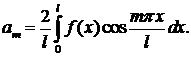
В случае, когда f(х)- нечетная функция, ее ряд Фурье содержит только синусы, т. е.
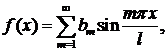
где

Если функция  задана на сегменте [0, l ], то для разложения в ряд Фурье достаточно доопределить ез на сегменте [— l, 0] произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на сегменте [— l, l ]. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках сегмента [— l, 0] находились из условия
задана на сегменте [0, l ], то для разложения в ряд Фурье достаточно доопределить ез на сегменте [— l, 0] произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на сегменте [— l, l ]. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках сегмента [— l, 0] находились из условия  = f (— х) или
= f (— х) или  = — f (— х). В первом случае функция
= — f (— х). В первом случае функция  на сегменте [— l, l ] будет четной, а во втором—нечетной. При этом коэффициенты разложения такой функции (ат в первом случае и bт — во втором) можно определить по вышеприведенным формулам для коэффициентов четных и нечетных функций.
на сегменте [— l, l ] будет четной, а во втором—нечетной. При этом коэффициенты разложения такой функции (ат в первом случае и bт — во втором) можно определить по вышеприведенным формулам для коэффициентов четных и нечетных функций.

485. Разложить в ряд Фурье периодическую функцию  с периодом 2π, заданную в интервале (—π, π) у равнением f(х)= π +х.
с периодом 2π, заданную в интервале (—π, π) у равнением f(х)= π +х.
∆ Графиком этой функции в интервале (—π, π) является отрезок, соединяющий точки (—π; 0) и (π;2π). На рис. 29 изображен график функции у=S(х), где S(x) —сумма ряда Фурье функции  . Эта сумма является периодической функцией с периодом 2 π и совпадает с функцией f(х) на сегменте [—π, π].
. Эта сумма является периодической функцией с периодом 2 π и совпадает с функцией f(х) на сегменте [—π, π].
Определяем коэффициенты ряда Фурье. Сначала находим
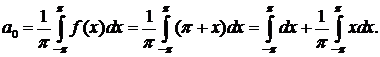
Второй интеграл равен нулю как интеграл от нечетной функции, взятый по интервалу, симметричному относительно начала координат. Таким образом, я

Далее, находим коэффициенты ат. Имеем

Нетрудно видеть, что оба интеграла равны нулю (подынтегральная функция второго интеграла является нечетной как произведение четной функции на нечетную). Итак, аm= 0, т. е. а1 = а2 = а3=... =0. Найдем теперь коэффициенты bт:

Первый интеграл равен нулю. Подынтегральная функция второго интеграла—четная как произведение двух нечетных функций. Таким образом,

Интегрируя по частям, получим  , т. е.
, т. е.

Следовательно, разложение функции f(x) в ряд Фурье имеет вид
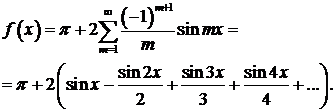 ▲
▲
486. Разложить в ряд Фурье периодическую функцию f(x) с периодом 2, заданную на сегменте [—1,1] уравнением f(х) = х2 (рис. 30).
∆ Рассматриваемая функция является четной. Ее график—дуга параболы, заключенная между точками (—1; 1) и (1; 1). Так как l=1, то
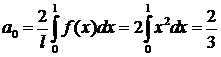

Здесь нужно дважды проинтегрировать по частям:
1) 




2) 
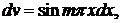
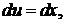
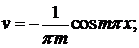

Так как рассматриваемая функция—четная, то bт = 0. Следовательно,

 ▲
▲
487. Разложить в ряд Фурье периодическую функцию, заданную на полупериоде [0,2] 
уравнением 
∆ Функция может быть разложена в ряд Фурье бесчисленным количеством способов. Рассмотрим два наиболее важных варианта разложения.
1) Доопределим функцию f(x) на сегменте [—2, 0] четным образом (рис. 31).
Имеем l= 2,


Интегрируем по частям:


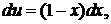

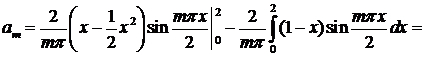

Еще раз интегрируем по частям:

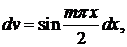





Итак,

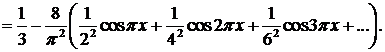
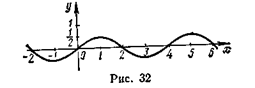
2) Доопределим функцию f(х) на сегменте [—2,0] нечетным образом (рис. 32):
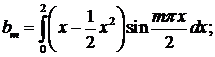
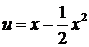 ,
, 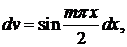
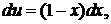












Итак,

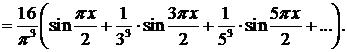 ▲
▲
488. Разложить в ряд Фурье периодическую функцию с периодом 2l (рис. 33), заданную на сегменте [—l, l] следующим образом:
0 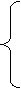 при -l ≤ x ≤ 0,
при -l ≤ x ≤ 0,
f(x)= x при 0 ≤ x≤ l/2,
l/2 при l/2 ≤x ≤ l.
∆ Находим



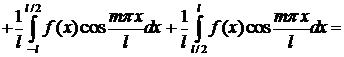


К первому интегралу применяем интегрирование по частям:

откуда



Определяем коэффициенты bm:

К первому интегралу применяем интегрирование по частям:
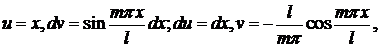
Имеем



Если  .
.

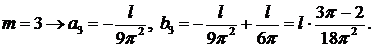


……………………………………………………
Следовательно,



Разложить в ряд Фурье периодическую функцию f (х) с периодом T, заданную на указанном сегменте.
489. f(х) = х; T= 2π; [—π, π ].
490. f(x) = |x|; Т = 2; [-1, 1].
491. f(x) = еx; Т = 2π; [— π, π].
492. f(х) = х3; Т = 2π; [— π, π].
493. f(х) = π —2x;; Т = 2π; [0, π]. Продолжить f(x) на сегмент
[—π, 0]: 1) четным образом; 2) нечетным образом.
494. 
495.  .
.
496. f(х) = х2 Т = 2 π; [0, π]. Продолжить f(x) на сегмент
[—π, 0] нечетным образом.
497. 
498. f(х) = соs 2х; T = 2 π; [0, π]. Разложить в ряд по синусам.
499. f(x) = x; Т = 2; [0, 1]. Разложить в ряд по синусам.
500. 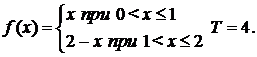 . Разложить в ряд по косинусам.
. Разложить в ряд по косинусам.
§ 9. ИНТЕГРАЛ ФУРЬЕ
Если функция f(х) удовлетворяет условиям Дирихле на любом конечном
отрезке оси Ox и абсолютно интегрируема вдоль всей оси (т. е. 
сходится), то для нее справедлива интегральная формула Фурье (получаемая
предельным переходом из ряда Фурье периодической функции с периодом 21 при l —>∞):

(в точках разрыва I рода по-прежнему за значение f (x) принимается (1/2) [f(х0 —0)+f(xо+0)], где х0 — абсцисса точки разрыва). Интеграл Фурье можно представить в комплексной форме:

Для четной функции интеграл Фурье может быть представлен в виде

а для нечетной функции—в виде

С тремя последними формулами связаны так называемые интегральные преобразования Фурье:
1. Преобразование Фурье общего вида:
 (обратное).
(обратное).
 (прямое).
(прямое).
2. Косинус-преобразование Фурье (для четных функций):
 (прямое),
(прямое),
 (обратное).
(обратное).
3. Синус-преобразование Фурье (для нечетных функций):
 (прямое),
(прямое),
 (обратное).
(обратное).
Синус- и косинус-преобразования Фурье могут применяться к функциям, заданным лишь на положительной полуоси Ох, если они абсолютно интегрируемы вдоль этой полуоси и удовлетворяют на любом ее конечном отрезке условиям Дирихле. При этом синус-преобразование продолжает функцию f(х) на отрицательную полуось нечетным образом, а косинус-преобразование — четным.
Примечание. В интегральных формулах Фурье все интегралы вида
 понимаются в смысле главного значения, т. е.
понимаются в смысле главного значения, т. е.

501. Найти косинус- и синус-преобразования функции 
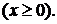
∆ Имеем

Так как  то
то

Аналогично получаем
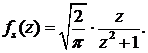
В свою очередь, применив косинус- и синус-преобразования Фурье к функциям  и
и  , получим функцию f (х), т. е
, получим функцию f (х), т. е


Отсюда получаем интегралы Лапласа:

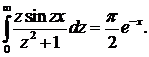 ▲
▲
502. Пусть функция f(х) определена равенствами
1  при 0 ≤ x < a
при 0 ≤ x < a
f(x)= 1/2 при x = a;
0 при x < 0.
Найти ее косинус- и синус-преобразования (рис. 34).

∆ Находим косинус-преобразование данной функции:


Найдем теперь синус-преобразование:


Отсюда получаем
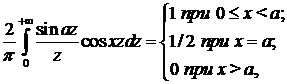
(разрывный множитель Дирихле) и

503. Найти преобразование Фурье функции

∆ По формуле преобразования Фурье

используя вид функции f(х), находим


Первый и последний интегралы, очевидно, равны нулю. Обозначим остальные интегралы соответственно через I1, I2 и I3 и вычислим их:
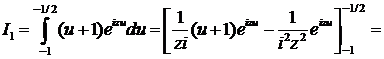




Итак,


504. Найти преобразование Фурье функции

505. Найти преобразование Фурье функции

506. Найти синус- и косинус-преобразования Фурье функции






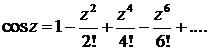
 (1)
(1) (2)
(2)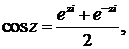 (3)
(3) (4)
(4) может быть представлено в показательной форме
может быть представлено в показательной форме 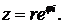


 Следовательно, тригонометрическая форма данного числа имеет вид
Следовательно, тригонометрическая форма данного числа имеет вид  а показательная форма—вид
а показательная форма—вид  ▲
▲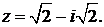

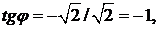
 т. е.
т. е.  ▲
▲


 то
то
 ▲
▲



 линейно через
линейно через  и
и  .
. имеет бесчисленное множество значений, которые все являются действительными.
имеет бесчисленное множество значений, которые все являются действительными. называется ряд
называется ряд (1)
(1)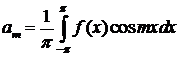 ,
, 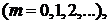
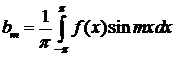 ,
, 
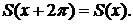
 имеет конечное число экстремумов и является непрерывной ва исключением конечного числа точек разрыва I рода (т. е. удовлетворяет так называемым условиям Дирихле). Тогда ряд Фурье этой функции сходится в каждой точке сегмента
имеет конечное число экстремумов и является непрерывной ва исключением конечного числа точек разрыва I рода (т. е. удовлетворяет так называемым условиям Дирихле). Тогда ряд Фурье этой функции сходится в каждой точке сегмента 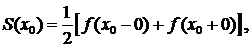 где x0—точка разрыва I рода функции f(х);
где x0—точка разрыва I рода функции f(х);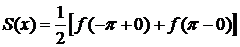 на концах промежутка, т.е. при
на концах промежутка, т.е. при 
 , где l —произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье
, где l —произвольное число, то при выполнении на этом сегменте условий Дирихле указанная функция может быть представлена в виде суммы ряда Фурье



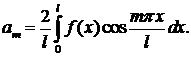
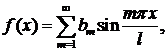

 задана на сегменте [0, l ], то для разложения в ряд Фурье достаточно доопределить ез на сегменте [— l, 0] произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на сегменте [— l, l ]. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках сегмента [— l, 0] находились из условия
задана на сегменте [0, l ], то для разложения в ряд Фурье достаточно доопределить ез на сегменте [— l, 0] произвольным способом, а затем разложить в ряд Фурье, считая ее заданной на сегменте [— l, l ]. Наиболее целесообразно функцию доопределить так, чтобы ее значения в точках сегмента [— l, 0] находились из условия 
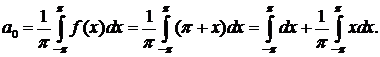




 , т. е.
, т. е.
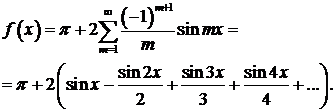 ▲
▲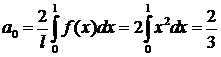







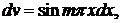
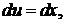
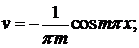


 ▲
▲





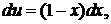

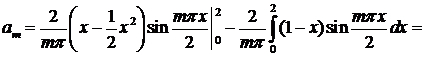


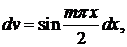






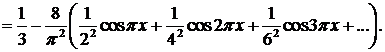

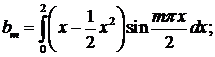
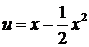 ,
, 







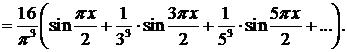 ▲
▲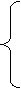 при -l ≤ x ≤ 0,
при -l ≤ x ≤ 0,


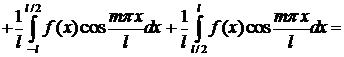







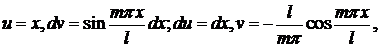



 .
.
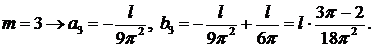






 .
.
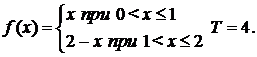 . Разложить в ряд по косинусам.
. Разложить в ряд по косинусам.




 (обратное).
(обратное). (прямое).
(прямое). (прямое),
(прямое), (обратное).
(обратное). (прямое),
(прямое), (обратное).
(обратное). понимаются в смысле главного значения, т. е.
понимаются в смысле главного значения, т. е.

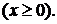

 то
то
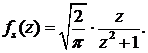
 и
и  , получим функцию f (х), т. е
, получим функцию f (х), т. е


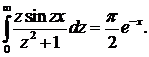 ▲
▲ при 0 ≤ x < a
при 0 ≤ x < a