

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
|
из
5.00
|
Заказать работу |
Здесь полезно иметь в виду приведенные в предыдущем параграфе разложения в степенные ряды функций ex, shx, chx, sinx, cosx, (1+x)m, ln(1+x), arctgx.
Для вычисления логарифмов эффективна формула
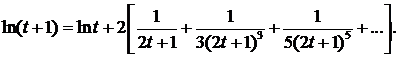
Ряд в правой части равенства сходится тем быстрее, чем больше t.
Для вычисления приближенного значения функции f(х) в ее разложении в степенной ряд сохраняют первые п членов (п- —конечная величина), а остальные члены отбрасывают. Для оценки погрешности найденного приближенного значения нужно оценить сумму отброшенных членов. Если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией. В случае знакопеременного ряда, члены которого удовлетворяют признаку Лейбница, используется оценка 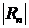 <
< 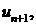 где
где 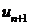 — первый из отброшенных членов ряда.
— первый из отброшенных членов ряда.
403. Оценить погрешность приближенного равенства
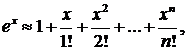 0 < x < n+1
0 < x < n+1
∆ Погрешность этого приближенного равенства определяется суммой членов, следующих после хп/п! в разложении ех:
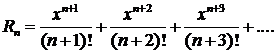
или
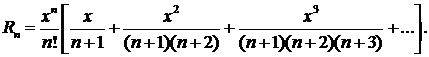
Заменив каждый из сомножителей n+2, n+3, n+4,... меньшей величиной n+1, получим неравенство
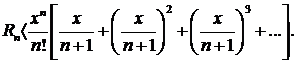
Просуммируем бесконечно убывающую геометрическую прогрессию в квадратных скобках:
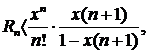 т.е.
т.е. 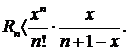 ▲
▲
404. Вычислить 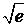 с точностью до 0,00001.
с точностью до 0,00001.
∆ Используя разложение ех в ряд, получаем
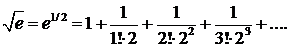
Определим число n так, чтобы погрешность приближенного равенства
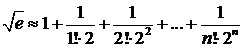
не превышала 0,00001. Воспользуемся оценкой погрешности, данной в предыдущем, примере. Полагаем х=1/2; тогда
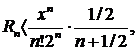 т.е.
т.е. 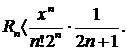
Путем подбора определим, при каком значении п будет выполняться неравенство Rп< 0,00001. Полагая, например, n= 3, получаем R3 < 1/(8·6·7), т. е. R3 < 1/336. Пусть, далее, n = 5; отсюда R5 < 1/(32·120·11 ), т. е. R5< 1/42240. Пусть, наконец, n= 6; отсюда R6 < 1/(64·720·13 ), т. е. R6 < 1/100000. Итак, принимаем п = 6:
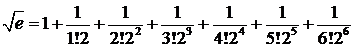 .
.
Суммируем слагаемые:
1,000000
0,500000
0,125000
+0,020833 (в 6 раз меньше предыдущего слагаемого)
0,002604 («8 ««««)
0,000260 («10 ««««)
0.000022 («12 ««««)
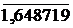 .
.
Значит, 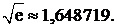 Каждое слагаемое мы вычислили с точностью до 0,000001, чтобы при суммировании не получить погрешности, превышающей 0,00001.
Каждое слагаемое мы вычислили с точностью до 0,000001, чтобы при суммировании не получить погрешности, превышающей 0,00001.
405. Вычислить 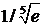 сточностью до 0,00001.
сточностью до 0,00001.
∆ Имеем
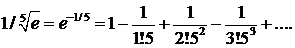
Воспользуемся приближенным равенством
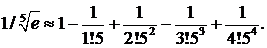
Мы взяли 5 слагаемых, так как знакопеременный ряд удовлетворяет условиям признака Лейбница, а поэтому допускаемая погрешность по абсолютной величине должна быть меньше первого из отброшенных членов ряда. Первый из отброшенных членов равен 1/(5!55). Нетрудно видеть, что 1/(5!55) < 0,00001.
Произведя вычисления, в результате получаем 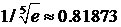 . ▲
. ▲
406. Пользуясь разложением соsx в ряд, вычислить соs 18° с точностью до 0,0001.
∆ Имеем
соs 18°= 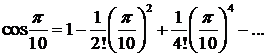 ;
;
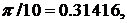
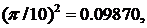
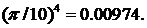
Достаточно взять три члена ряда, так как (1/6!)-(π/10)6 < 0,0001. Тогда
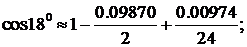
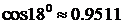 . ▲
. ▲
407. Вычислить 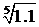 с точностью до 0,0001.
с точностью до 0,0001.
∆ Воспользуемся разложением (1+x)m в ряд, полагая x = 0,1, m=1/5.
Имеем
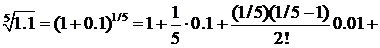
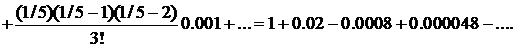
Четвертый и следующие за ним члены отбрасываем, так как четвертый член меньше 0,0001. Итак, 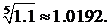 ▲
▲
408. Вычислить 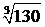 с точностью до 0,001.
с точностью до 0,001.
∆ Так как 53 является ближайшим к числу 130 кубом целого числа, то целесообразно число 130 представить в виде суммы двух слагаемых: 130 = 53 + 5. Тогда
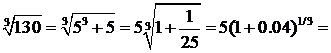
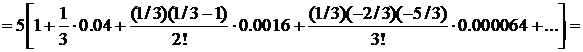
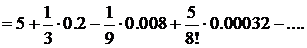
Четвертый член меньше 0,001, поэтому его и следующие за ним члены можно отбросить. Итак, 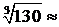 5 + 0,0667—0,0009, т. е.
5 + 0,0667—0,0009, т. е. 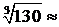 5,066. ▲
5,066. ▲
409. Вычислить ln1,04 с точностью до 0,0001.
∆ Воспользуемся разложением ln(1+ x) в ряд:
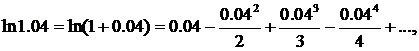
или
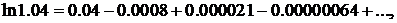
откуда ln1,04≈ 0,0392. ▲
410. В прямоугольном треугольнике катеты равны 1 и 5 см. Определить острый угол треугольника, лежащий против меньшего катета, с точностью до 0,001 радиана.
∆ Так как tgα=1/5, то α=arctg(1,5). Воспользуемся разложением
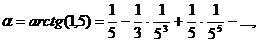
откуда α ≈ 0,2—0,0027, т. е. α ≈ 0,197. ▲
411. Оценить погрешность приближенного равенства
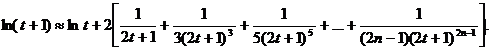
∆ Задача сводится к оценке суммы остатка ряда
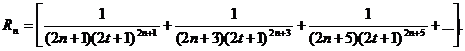
Заменив каждый из множителей 2n+З, 2n + 5, 2n+7,... меньшим числом 2n+1, получим неравенство
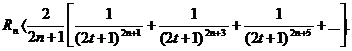
Просуммируем бесконечно убывающую геометрическую прогрессию в квадратных скобках:
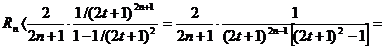
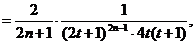 т.е.
т.е. 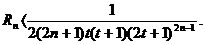 ▲
▲
412. Вычислить ln2 с точностью до 0,0001.
∆ В формуле для определения ln(t + 1) и неравенстве для оценки Rп полагаем t= 1:
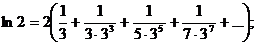
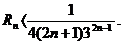
Путем подбора определим п так, чтобы выполнялось неравенство Rn< 0,0001. Если n= 2, то R2 < 1/(4∙5∙33); R2 < 1/540; если n = 3, то R3 < 1(4∙7∙35); R3 < 1/6804; если n= 4, то R4 < 1/(4∙9∙37); R4 < 1/10000.
Итак, n = 4 и для вычисления ln 2 получаем приближенное равенство

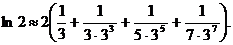
Суммируя эти четыре слагаемых, получим
ln2 ≈ 0,66667 + 0,02469+0,00165+0,00013 = 0,69314≈ 0,6931. ▲
413. Вычислить ln5 с точностью до 0,0001.
∆ Полагаем t= 4. Тогда
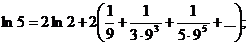
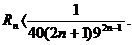
Если n=1, то R1<1/(40∙3∙93); R1< 1/1080; если n= 2, то R2< < 1/(40∙5∙93); R2 < 1/10000. Значит, достаточно взять два члена ряда. Следовательно,
ln5 ≈ 2ln2+2 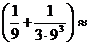 1,38628+0,22222+0,00090=1,60940. ▲
1,38628+0,22222+0,00090=1,60940. ▲
414. Доказать справедливость тождества π/4 = агсtg (1/2)+ агсtg(1/3) и вычислить πс точностью до 0,001.
∆ Полагая в равенстве
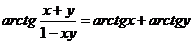
x=1/2, y=1/3, получаем
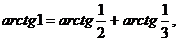 или π = 4 (
или π = 4 (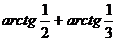 ).
).
Воспользовавшись разложением arctg х в ряд, имеем
π = 4 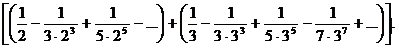
Выполняя вычисления, находим π = 3,1416.
Для вычисления числа π можно было воспользоваться рядами, которые сходятся быстрее, чем только что приведенные. ▲
Вычислить:
415. е с точностью до 0,00001.
415. 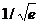 с точностью до 0,00001.
с точностью до 0,00001.
416. sin9°C с точностью до 0,0001.
417. сh О,3 с точностью до 0,0001.
418. 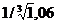 точностью до 0,0001.
точностью до 0,0001.
419. 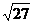 с точностью до 0,001.
с точностью до 0,001.
420. ln 0,98 с точностью до 0,0001.
421. ln 1,1 с точностью до 0,0001.
422. ln З с точностью до 0,0001.
423. ln 10 с точностью до 0,0001.
424. Найти наименьшее положительное значение х, удовлетворяющее тригонометрическому уравнению 2sinх—соsx=0.
425. Вычислить π с точностью до 0,001, полагая x= 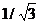
в разложении аrctg х.

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!