Определение производной
Пусть функция  определена и непрерывна на интервале
определена и непрерывна на интервале  . Зададим аргументу
. Зададим аргументу 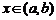 некоторое приращение
некоторое приращение 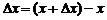 , тогда функция
, тогда функция  получит приращение
получит приращение 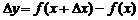 . Составим отношение приращения функции к приращению аргумента:
. Составим отношение приращения функции к приращению аргумента:
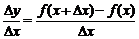 .
.
Рассмотрим предел этого отношения при 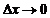 :
:
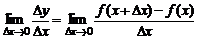 .
.
Определение. Производной функции  в точке x называется предел (если он существует) отношения приращения функции
в точке x называется предел (если он существует) отношения приращения функции 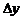 к приращению аргумента
к приращению аргумента 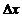 , когда последнее стремится к нулю (
, когда последнее стремится к нулю (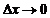 ).
).
Таким образом, получаем
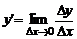 (16)
(16)
или
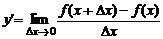 . (17)
. (17)
Замечание. При вычислении производной функции по опреде-лению возникает неопределенное выражение вида  . Раскрывая эту неопределенность, выясняем существование предела и тем самым производной функции в точке x.
. Раскрывая эту неопределенность, выясняем существование предела и тем самым производной функции в точке x.
Для обозначения производной функции  часто используют также символы:
часто используют также символы:
 ,
, 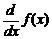 ,
, 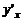 .
.
Если в каждой точке 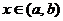 существует производная
существует производная 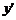 , то функция
, то функция  называется дифференцируемой на интервале
называется дифференцируемой на интервале  , а операция нахождения производной функции называется дифференцированием.
, а операция нахождения производной функции называется дифференцированием.
Геометрический смысл производной
Касательной к кривой  в точке
в точке 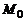 называется прямая, являющаяся предельным положением секущей
называется прямая, являющаяся предельным положением секущей 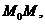 когда точка M, двигаясь по кривой, неограниченно прибли-жается к точке
когда точка M, двигаясь по кривой, неограниченно прибли-жается к точке 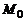 (рис. 9.1).
(рис. 9.1).
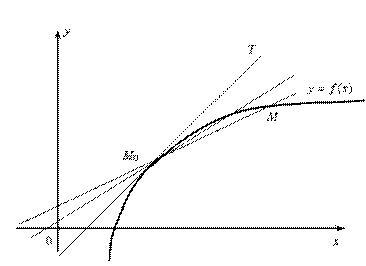
Рис. 9.1
Рассмотрим график непрерывной на  функции
функции  (рис. 9.2), имеющей в точке
(рис. 9.2), имеющей в точке 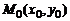 невертикальную касате-льную. Найдем угловой коэффициент этой касательной:
невертикальную касате-льную. Найдем угловой коэффициент этой касательной: 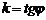 , где j – угол наклона касательной к оси
, где j – угол наклона касательной к оси 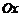 .
.
Придадим переменной x приращение 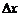 , функция
, функция  также получит приращение
также получит приращение 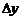 , соответствующей ему точкой на кривой будет
, соответствующей ему точкой на кривой будет 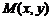 , где
, где 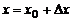 ,
,  . Проведем секущую
. Проведем секущую 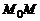 и обозначим через y угол между секущей
и обозначим через y угол между секущей 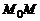 и осью Ox. Рассмотрим треугольник
и осью Ox. Рассмотрим треугольник 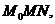 тогда
тогда 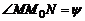 . Угловой коэффициент секущей равен
. Угловой коэффициент секущей равен
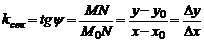 .
.
Из непрерывности функции следует, что при 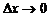 приращение
приращение 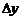 также стремится к нулю; но тогда точка М, двигаясь по кривой, в пределе совпадает с точкой
также стремится к нулю; но тогда точка М, двигаясь по кривой, в пределе совпадает с точкой 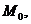 а секущая, поворачиваясь в точке
а секущая, поворачиваясь в точке 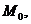 в пределе переходит в касательную, тогда
в пределе переходит в касательную, тогда
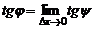 .
.
Поэтому угловой коэффициент касательной равен:
 .
.
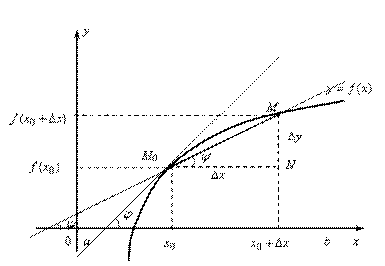
Рис. 9.2
Таким образом, геометрически производная 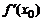 в точке
в точке 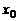 равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции  в точке, абсцисса которой равна
в точке, абсцисса которой равна 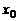 , или, что то же самое, тангенсу угла наклона касательной в точке
, или, что то же самое, тангенсу угла наклона касательной в точке 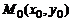 к оси абсцисс.
к оси абсцисс.
Правила дифференцирования, таблица производных
Для вычисления производных необходимо знать правила дифференцирования и формулы, определяющие производные прос-тейших функций. Вывод этих правил и формул основывается на определении производной функции.
Правила дифференцирования
Пусть 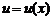 ,
, 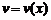 – дифференцируемые функции на интервале
– дифференцируемые функции на интервале  ,
, 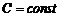 .
.
1. 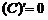 .
.
Доказательство. Пусть 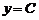 , придадим переменной
, придадим переменной 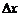 приращение, тогда
приращение, тогда 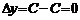 . Составим отношение
. Составим отношение 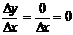 и вычислим предел
и вычислим предел 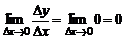 .
.
2. 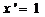 .
.
Доказательство. Пусть  , тогда
, тогда 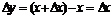 ,
, 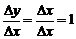 . По определению имеем
. По определению имеем  .
.
3. 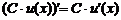 .
.
Доказательство. Пусть 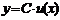 и функция
и функция  – дифференцируемая на интервале
– дифференцируемая на интервале  , т. е.
, т. е. 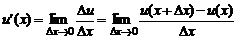 . Придадим переменной x приращение, тогда функции y, u также получат приращение:
. Придадим переменной x приращение, тогда функции y, u также получат приращение:
 ,
, 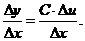 Переходя к пределу при
Переходя к пределу при 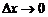 , получаем
, получаем 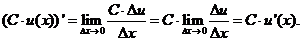
4. 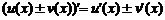 .
.
Доказательство. Пусть 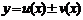 ,
, 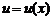 ,
, 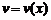 – дифференцируемые функции на интервале
– дифференцируемые функции на интервале  , т. е.
, т. е.
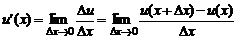 ,
, 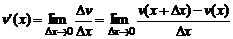 .
.
Запишем приращение функции, соответствующее приращению переменной 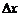 :
:
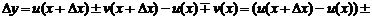
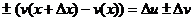 .
.
По определению производной и свойствам пределов функций получаем:
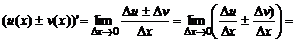
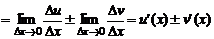 .
.
5. 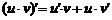 .
.
Доказательство. Пусть 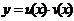 , где
, где 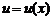 ,
, 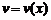 – дифференцируемые функции на интервале
– дифференцируемые функции на интервале  :
:
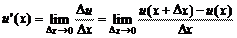 ,
, 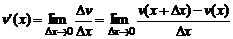 .
.
Если независимая переменная получит приращение 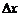 , тогда функции y, u, v также получат приращение, т. е.
, тогда функции y, u, v также получат приращение, т. е.
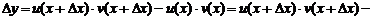
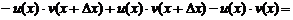

 .
.
По определению производной и свойствам пределов функций получаем:
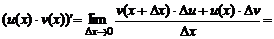
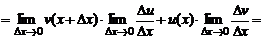
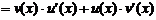 .
.
6. 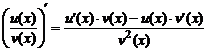 ,
, 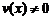 .
.
Доказательство. Пусть 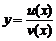 ,
, 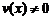 и
и 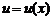 ,
, 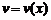 – дифференцируемые функции на интервале
– дифференцируемые функции на интервале 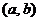 :
:
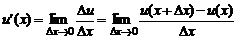 ,
, 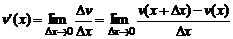 .
.
Приращению 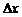 соответствуют приращения функций
соответствуют приращения функций
y, u, v, тогда:
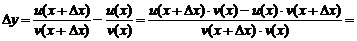
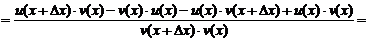
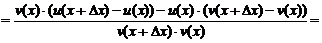
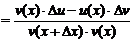 .
.
По определению производной и свойствам пределов функций имеем:
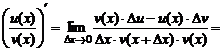
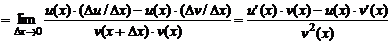 .
.
Пример 9.1. Найти производную функции по определению: 1)  ; 2)
; 2) 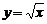 ; 3)
; 3)  .
.
Решение
1)  . Значению независимой переменной x соответ-ствует значение функции
. Значению независимой переменной x соответ-ствует значение функции 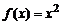 ,
, 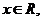 значению
значению 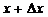 соответствует значение функции
соответствует значение функции 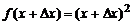 . По оп-ределению производной (17) имеем:
. По оп-ределению производной (17) имеем:
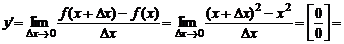
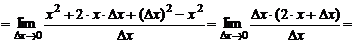
 . Таким образом,
. Таким образом, 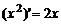 .
.
2) 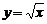 . Запишем приращение функции
. Запишем приращение функции 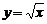 , соответ-ствующее приращению независимой переменной
, соответ-ствующее приращению независимой переменной 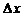 (
(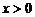 ):
): 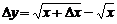 . По определению производной функции имеем:
. По определению производной функции имеем:
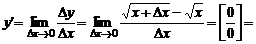
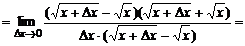
 ,
,
т. е. 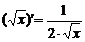 .
.
3) 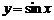 . Значению аргумента x соответствует значение функции
. Значению аргумента x соответствует значение функции 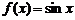 , а значению
, а значению 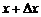 соответствует значение функции
соответствует значение функции  .
.
Найдем приращение функции:
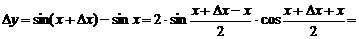
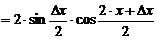 ,
,
вычислим предел:
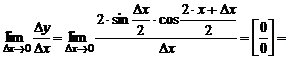
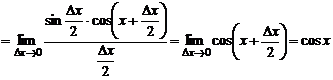 .
.
Таким образом, получаем 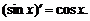
Таблица производных простейших функций
| 1)
| 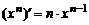 , , 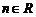 ; ;
| 8)
| 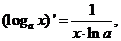 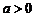 , , 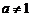 ; ;
|
| 2)
| 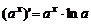 , , 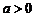 , , 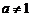 ; ;
| 9)
|  ; ;
| |
| 3)
| 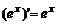 ; ;
| 10)
| 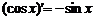 ; ;
| |
| 4)
| 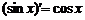 ; ;
| 11)
| 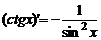 ; ;
| |
| 5)
| 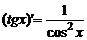 ; ;
| 12)
| 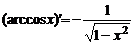 ; ;
| |
| 6)
|  ; ;
| 13)
| 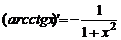 . .
| |
| 7)
| 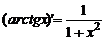 ; ;
| |
| |
| | | | | | |
Пример 9.2. Найти производную функции:
1)  2)
2) 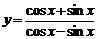 .
.
Решение
1) Воспользуемся правилом дифференцирования произведения функций:
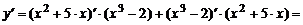
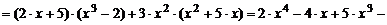
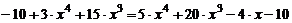 .
.
2) По правилу дифференцирования дроби имеем:
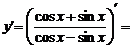
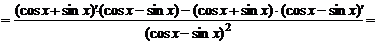
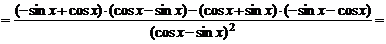
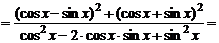
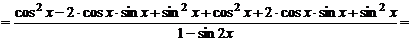
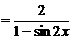 .
.



 определена и непрерывна на интервале
определена и непрерывна на интервале  . Зададим аргументу
. Зададим аргументу 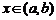 некоторое приращение
некоторое приращение 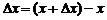 , тогда функция
, тогда функция 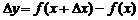 . Составим отношение приращения функции к приращению аргумента:
. Составим отношение приращения функции к приращению аргумента: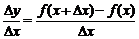 .
.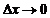 :
: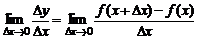 .
.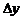 к приращению аргумента
к приращению аргумента 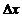 , когда последнее стремится к нулю (
, когда последнее стремится к нулю (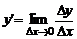 (16)
(16)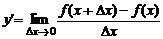 . (17)
. (17) . Раскрывая эту неопределенность, выясняем существование предела и тем самым производной функции в точке x.
. Раскрывая эту неопределенность, выясняем существование предела и тем самым производной функции в точке x. ,
, 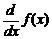 ,
, 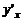 .
.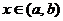 существует производная
существует производная 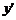 , то функция
, то функция 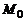 называется прямая, являющаяся предельным положением секущей
называется прямая, являющаяся предельным положением секущей 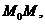 когда точка M, двигаясь по кривой, неограниченно прибли-жается к точке
когда точка M, двигаясь по кривой, неограниченно прибли-жается к точке 
 (рис. 9.2), имеющей в точке
(рис. 9.2), имеющей в точке 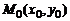 невертикальную касате-льную. Найдем угловой коэффициент этой касательной:
невертикальную касате-льную. Найдем угловой коэффициент этой касательной: 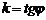 , где j – угол наклона касательной к оси
, где j – угол наклона касательной к оси 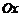 .
.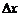 , функция
, функция 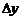 , соответствующей ему точкой на кривой будет
, соответствующей ему точкой на кривой будет 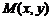 , где
, где 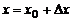 ,
,  . Проведем секущую
. Проведем секущую 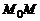 и обозначим через y угол между секущей
и обозначим через y угол между секущей 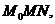 тогда
тогда 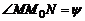 . Угловой коэффициент секущей равен
. Угловой коэффициент секущей равен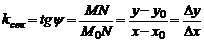 .
.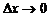 приращение
приращение 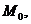 а секущая, поворачиваясь в точке
а секущая, поворачиваясь в точке 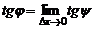 .
. .
.
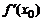 в точке
в точке 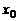 равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции 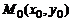 к оси абсцисс.
к оси абсцисс.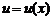 ,
, 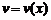 – дифференцируемые функции на интервале
– дифференцируемые функции на интервале  ,
, 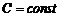 .
.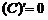 .
.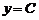 , придадим переменной
, придадим переменной 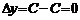 . Составим отношение
. Составим отношение 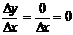 и вычислим предел
и вычислим предел 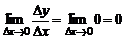 .
.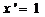 .
. , тогда
, тогда 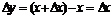 ,
, 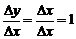 . По определению имеем
. По определению имеем  .
.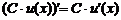 .
.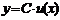 и функция
и функция  – дифференцируемая на интервале
– дифференцируемая на интервале 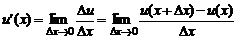 . Придадим переменной x приращение, тогда функции y, u также получат приращение:
. Придадим переменной x приращение, тогда функции y, u также получат приращение: ,
, 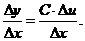 Переходя к пределу при
Переходя к пределу при 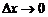 , получаем
, получаем 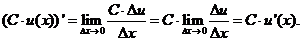
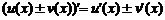 .
.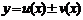 ,
, 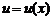 ,
, 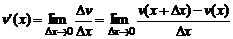 .
.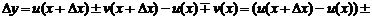
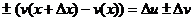 .
.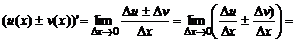
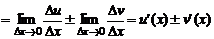 .
.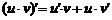 .
.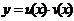 , где
, где 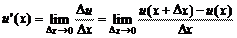 ,
, 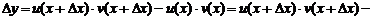
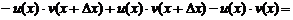

 .
.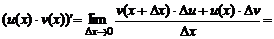
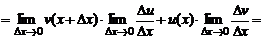
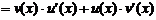 .
.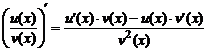 ,
, 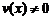 .
.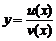 ,
, 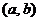 :
: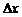 соответствуют приращения функций
соответствуют приращения функций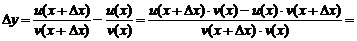
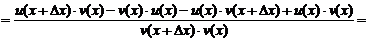
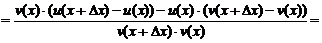
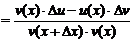 .
.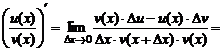
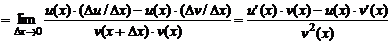 .
. ; 2)
; 2) 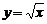 ; 3)
; 3)  .
.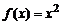 ,
, 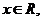 значению
значению 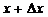 соответствует значение функции
соответствует значение функции 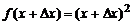 . По оп-ределению производной (17) имеем:
. По оп-ределению производной (17) имеем: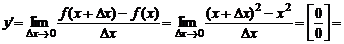
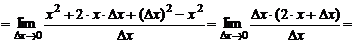
 . Таким образом,
. Таким образом, 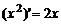 .
.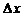 (
(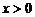 ):
): 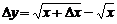 . По определению производной функции имеем:
. По определению производной функции имеем: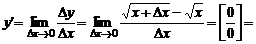
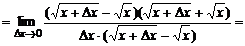
 ,
,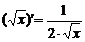 .
.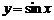 . Значению аргумента x соответствует значение функции
. Значению аргумента x соответствует значение функции 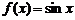 , а значению
, а значению 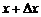 соответствует значение функции
соответствует значение функции  .
.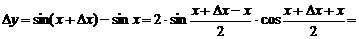
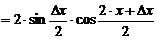 ,
,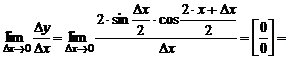
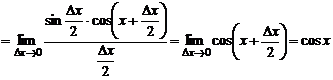 .
.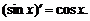
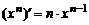 ,
, 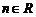 ;
;
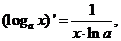
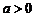 ,
, 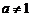 ;
;
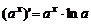 ,
,  ;
;
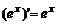 ;
;
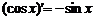 ;
;
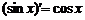 ;
;
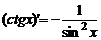 ;
;
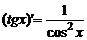 ;
;
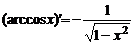 ;
;
 ;
;
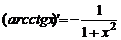 .
.
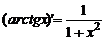 ;
;
 2)
2) 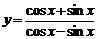 .
.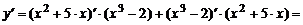
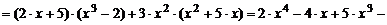
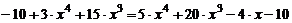 .
.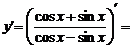
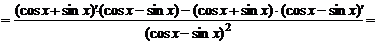
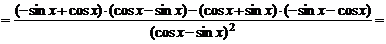
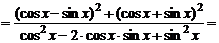
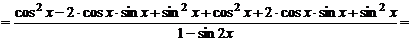
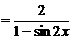 .
.

