Вероятность попадания нормального распределения в заданный интервал вычисляется по формуле: 
31. Правило «трех σ»
Найдём вероятность того, что нормально распределенная величина примет значение из интервала(a-3σ, a+3σ)
P (a-3σ <x<a+3σ) = Ф (3) – Ф (-3) = 0, 9973
Следовательно, вероятность того, что значение СВ окажется вне данного интервала будет равна 0,27% и может считаться пренебрежительно малой.
Правило «трёх σ»: если случайная величина распределена нормально, то модуль её отклонения от x=a не превосходит трех сигм.
Начальные и центральные теоретические моменты. Асимметрия и эксцесс.
Начальным моментом порядка k случайной величины X называется математическое ожидание величины  :
:



Центральным моментом k-го порядка случайной величины X называется математическое ожидание величины:
μk=M ((X-M(X))k)
μ2=M ((X-M(X))2)=D(X)

Существует связь между начальными и центральными моментами, и эта связь выражается в след. соотношениях:
μ2=ν2 – ν12
μ3=ν3 – 3ν1ν2+2ν12
μ4=ν4 – 4ν1ν3+6 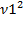 ν2 –3ν14
ν2 –3ν14
Коэффициентом асимметрии случайной величины называется величина, равная отношению центрального момента 3-го порядка к кубу среднеквадратического отклонения:

На рисунке показано два асимметричных распределения; одно из них (кривая I) имеет положительную асимметрию ( ); другое (кривая II) – отрицательную (
); другое (кривая II) – отрицательную ( ).
).

Эксцессом случайной величины называется величина равная: 
На рисунке представлены: нормальное распределение (кривая I), распределение с положительным эксцессом (кривая II) и распределение с отрицательным эксцессом (кривая III).

Закон больших чисел: неравенство Маркова, неравенство и теорема Чебышева. Сущность и значение теоремы Чебышева для практики.
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому по формулировке Колмогорова совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая, т.е. при большом числе случайных величин их средний результат перестаёт быть случайным и может быть предсказан с большей степенью определенности.
Под законом больших чисел (ЗБЧ) в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Неравенства Маркова.
Если случайная величина X принимает только неотрицательные значения и имеет математическое ожидание М(Х), то для любого положительного числа А верно неравенство:

 )
)
Неравенства Маркова применимо к любым неотрицательным случайным величинам.
Неравенство Чебышева.
Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо след. неравенство:
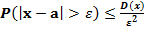 (1)
(1)
где а = М(x), ε >0 –достаточно малое число, но положительное число
Учитывая, что события по модулю |x-a| >  и |x-a| <
и |x-a| <  противоположны, неравенство Чебышева можно записать в другой форме:
противоположны, неравенство Чебышева можно записать в другой форме:
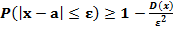 (2)
(2)
Неравенство Чебышева применимо для любых случайных величин. Неравенство Чебышева (1) устанавливает верхнюю границу, (2) – нижнюю границу вероятности рассматриваемого объекта.
Рассмотрим частные случаи для некоторых случайных величин:
1) Для случайных величин Х=m величина имеет биномиальное распределение, для неё математическое ожидание M(x)=np, а дисперсия D(x)=npq, тогда неравенство Чебышева будет иметь вид:  (3)
(3)
2) Для частоты  события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=
события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=  , тогда неравенство Чебышева примет вид:
, тогда неравенство Чебышева примет вид:
 (4)
(4)
Теорема Чебышева.
При большом числе n среднее арифметическое случайных величин X1, X2,.., Xn сколь угодно мало отличается от неслучайной величины  .
.
Теорема Чебышева имеет вид: 
Сущность теоремы Чебышева: хотя отдельные независимые случайные величины могут принимать значения, далекие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения, близкие к определенному постоянному числу, а именно к числу 
(или к числу а в частном случае). Иными словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало.




 :
:



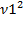 ν2 –3ν14
ν2 –3ν14
 ); другое (кривая II) – отрицательную (
); другое (кривая II) – отрицательную ( ).
).



 )
)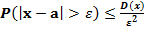 (1)
(1) и |x-a| <
и |x-a| < 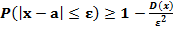 (2)
(2) (3)
(3) события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=
события в n независимых испытаниях, в каждой из которых событие появляется с вероятностью p, а=M(x)=p, а D(x)=  , тогда неравенство Чебышева примет вид:
, тогда неравенство Чебышева примет вид:  (4)
(4)




