Условия вариантов задачи
В задачах 6.1-6.40 (параметры заданий приведены в табл. 6.1) случайная величина Х задана плотностью вероятности


Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал  .
.
Таблица 6.1
| Вариант
| 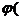 x,c) x,c)
| a
| b
| a
| b
|
| 6.1
| 
| -3
|
| -0,5
| 1,5
|
| 6.2
| 
|
|
| 0,5
|
|
| 6.3
| 
| -1
|
|
| 0,5
|
| 6.4
| 
| -1
|
| -1
|
|
| 6.5
| 
|
|
| -2
|
|
| 6.6
| 
| -2
|
| -1
|
|
| 6.7
| 
|
| p/2
| p/4
| p/2
|
| 6.8
| 
|
| p/2
| p/4
| p
|
| 6.9
| 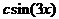
|
| p/3
| -1
|
|
| 6.10
| 
| -p/2
| p/2
|
|
|
| 6.11
| 
| -p/4
| p/4
| 0,5
|
|
| 6.12
| c e-x
|
| 
|
|
|
| 6.13
| c e-2x
|
| 
|
|
|
| 6.14
| 5 e-cx
|
| 
|
|
|
| 6.15
| c 
| -2
|
| 1,5
|
|
| 6.16
| c ex
|
|
|
| 0,5
|
| 6.17
| c x5
|
|
| 0,5
| 0,7
|
| 6.18
| c x6
| -1
|
|
|
|
| 6.19
| c x7
|
|
|
| 0,25
|
| 6.20
| c x8
| -1
|
|
|
|
| 6.21
| c x9
|
|
|
| 0,25
|
| 6.22
| c x10
| -1
|
| -0,5
| 0,5
|
| 6.23
| 
|
|
|
|
|
| 6.24
| 
|
|
|
| 2,5
|
| 6.25
| 
|
|
|
| 1,5
|
| 6.26
| 
|
|
|
|
|
| 6.27
| 
|
|
|
|
|
| 6.28
| 
|
|
|
| 1,5
|
| 6.29
| 
|
|
|
|
|
| 6.30
| 
|
|
|
|
|
| 6.31
| 
|
|
| 0,5
| 1,5
|
| 6.32
| 
|
|
|
|
|
| 6.33
| 
|
| p
|
| p/2
|
| 6.34
| 
| -p/6
| p/6
|
|
|
| 6.35
| c x5
|
|
|
|
|
| 6.36
| c x6
| -2
|
| -1
|
|
| 6.37
| c x7
|
|
| 0,5
| 0,7
|
| 6.38
| c x8
| -2
|
| -0,5
| 0,25
|
| 6.39
| c x9
|
|
|
| 1,5
|
| 6.40
| c x10
| -2
|
| -1
| 1,5
|
Методические указания
Случайная величина Х называется непрерывной, если ее функция распределения F(x) – непрерывная и дифференцируемая функция для всех значений аргумента.
Плотность распределения (или плотность вероятности) f (x) непрерывной случайной величины X в точке x характеризует плотность вероятности в окрестностях точки x и равна производной функции распределения этой СВ:
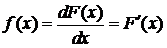 . (6.1)
. (6.1)
График плотности распределения называется кривой распределения.
Вероятность попадания случайной величины X на произвольный участок 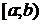 равна сумме элементарных вероятностей на этом участке:
равна сумме элементарных вероятностей на этом участке:
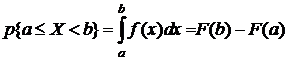 . (6.2)
. (6.2)
В геометрической интерпретации вероятность 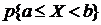 равна площади, ограниченной сверху кривой распределения f (x) и отрезком
равна площади, ограниченной сверху кривой распределения f (x) и отрезком 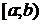 .
.
Соотношение (6.2) позволяет выразить функцию распределения F (x) случайной величины X через ее плотность:
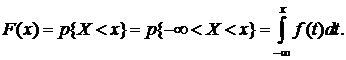 (6.3)
(6.3)
Основные свойства плотности распределения:
1. Плотность распределения неотрицательна: f (x) 0. Причем f (x) = 0 для тех значений x, которые СВ никогда не принимает в опыте.
2. Условие нормировки:
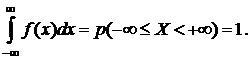 (6.4)
(6.4)
Математическое ожидание характеризует среднее значение случайной величины и для непрерывной СВ определяется по формуле
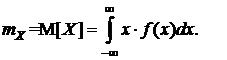 (6.5)
(6.5)
Дисперсияслучайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и для непрерывной СВ определяется по формуле
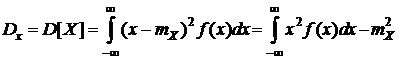 . (6.6)
. (6.6)
Дисперсия случайной величины имеет размерность квадрата случайной величины, поэтому для анализа диапазона значений величины Х дисперсия не совсем удобна. Этого недостатка лишено среднее квадратическое отклонение (СКО), размерность которого совпадает с размерностью случайной величины.
Среднее квадратическое отклонение случайной величины X характеризует ширину диапазона значений X и равно
 . (6.7)
. (6.7)
Правило  . Практически все значения случайной величины находятся в интервале
. Практически все значения случайной величины находятся в интервале
 . (6.8)
. (6.8)
Примеры
Пример 6.1. Случайная величина X распределена по закону, определяемому плотностью вероятности вида

Определить константу с, функцию распределения F(x), математическое ожидание, дисперсию величины Х, а также вероятность ее попадания в интервал  .
.
Решение. Вначале вычислим значение константы с из условия нормировки (6.4). Условие нормировки представляет собой интегральное уравнение, из которого можно определить неизвестный параметр плотности вероятности. Для этого определим значение интеграла в левой части условия нормировки:
 .
.
Из условия нормировки следует:
 .
.
Плотность вероятности примет вид

Определим функцию распределения F(x). Так как плотность вероятности задана различными формулами на разных интервалах, то и ее первообразную - функцию распределения – будем искать по формуле (6.3) для каждого интервала в отдельности.
Для  :
:  ,
,
для  :
:  ,
,
для  :
: 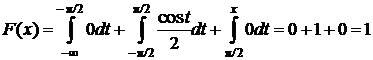 .
.
Окончательно имеем

Вычислим вероятность  по формуле (6.2):
по формуле (6.2):
 .
.
Так как правый край интервала  больше, чем
больше, чем  , то
, то  .
.
Вычислим математическое ожидание СВ по формуле (6.5):

Дисперсиюслучайной величины СВ вычислим по формуле (6.6):

Пример 6.2. Определить по правилу  диапазон возможных значений СВ X из примера 6.1.
диапазон возможных значений СВ X из примера 6.1.
Решение. Вычислим среднее квадратическое отклонение СВ по формуле (6.7):

Оценим диапазона значений X по формуле (6.8):

Как видим, получился интервал, полностью охватывающий точный диапазон значений СВ  , который можно определить по свойству 1 плотности вероятности.
, который можно определить по свойству 1 плотности вероятности.





 .
.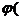 x,c)
x,c)








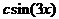















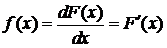 . (6.1)
. (6.1)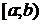 равна сумме элементарных вероятностей на этом участке:
равна сумме элементарных вероятностей на этом участке: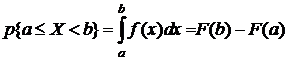 . (6.2)
. (6.2)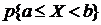 равна площади, ограниченной сверху кривой распределения f (x) и отрезком
равна площади, ограниченной сверху кривой распределения f (x) и отрезком 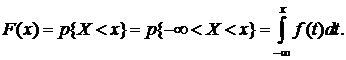 (6.3)
(6.3)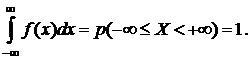 (6.4)
(6.4)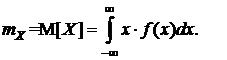 (6.5)
(6.5)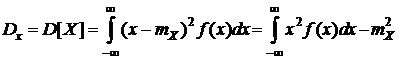 . (6.6)
. (6.6) . (6.7)
. (6.7) . Практически все значения случайной величины находятся в интервале
. Практически все значения случайной величины находятся в интервале . (6.8)
. (6.8)
 .
. .
. .
.
 :
:  ,
, :
:  ,
, :
: 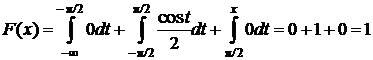 .
.
 по формуле (6.2):
по формуле (6.2): .
. , то
, то  .
.



 , который можно определить по свойству 1 плотности вероятности.
, который можно определить по свойству 1 плотности вероятности.


