Матрицы и основные действия над ними. Пример умножения двух матриц.
I. Сложение. Матрицы можно сложить, если у них одинаковые порядки. Если матрица  и матрица
и матрица 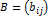 , то
, то 
Например:
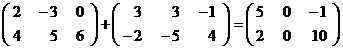 .
.
II. Умножение на число. Если матрица  и
и  – число,то
– число,то  .
.
Например: если число  = 2 и матрица
= 2 и матрица  , то
, то 

III. Умножение матриц. МатрицыА и В можно перемножить, если число столбцов матрицы А совпадает с числом строк матрицы В.
Например, нельзя перемножать две матрицы
 и В =
и В = 
Матрицы умножаются специальным правилом, например,


В общем случае АВ не равно ВА, но если это равенство выполняется, то матрицыА и В называются коммутирующими друг другу.
Матрица А-1 называется обратной матрицей А, если выполняются соотношения:

Выполняются следующие свойства:
(А + В) + С = А + (В + С)

(A-1)-1 = A
(А  В)
В)  С = А
С = А  (В
(В  С)
С)
(А  В)-1 =B-1
В)-1 =B-1  A-1
A-1
3. Элементарные преобразования над матрицами. Эквивалентные матрицы. Приведение матриц к ступенчатому виду, пример.
Под элементарными преобразованиями над матрицей понимают:
1. Вычеркивание 0-го ряда;
2. Замена местами любых двух параллельных рядов;
3. Умножение на ненулевое число.
4. Транспонирование.
5. Умножение любого ряда на число.
6. Прибавление к любому ряду параллельного ряда, умноженное на любое ненулевое число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.
С помощью таких преобразований любую матрицу можно привести к ступенчатому (треугольному) виду; более того матрицу можно преобразовать таким образом, что останутся в конечном счете только 0 и 1. Число полученных 1 составляет ранг матрицы.
Пример. Привести матрицу к ступенчатому виду.
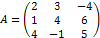
1. Меняем местами 1-ю и 2-ю строки, тогда

2. (-2) умножили на первую строку и прибавили ко 2-й строке; затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.
3. 
 затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.
затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.







4. Вторую строку умножили на (-17/5) и прибавили к 3-ей.





Определители 2-го и 3-го порядка и методы их вычисления. Примеры.
Понятие определителя - число, характеризующее квадратную матрицу  , необходимо для решения систем линейных алгебраических уравнений.
, необходимо для решения систем линейных алгебраических уравнений.
Определитель матрицы  обозначают
обозначают  ,
,  ,
,  .
.
1) Определителем матицы 1-го порядка 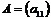 , называется элемент
, называется элемент 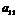 :
:  ;
;
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
 . Произведения
. Произведения  называются членами определителя 2-го порядка.
называются членами определителя 2-го порядка.
Примеры:
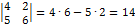

3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
 .
.
Данная формула получила название правила треугольников или правило Саррюса. Оно символически записывается так:

 .
.
Примеры: Вычислить определитель матрицы
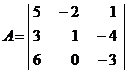 .
.
Решение: 

 .
.
Система трех линейных неоднородных алгебраических уравнений: определение и метод Крамера решения. Пример.
К такой относится система вида

Здесь 
Если хотя бы один свободный коэффициент не равен 0, то система называется неоднородной, если же  – однородной. Однородная система обозначается символом
– однородной. Однородная система обозначается символом 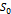 и всегда имеет решение (хотя бы нулевое).
и всегда имеет решение (хотя бы нулевое).
Неоднородная система совместна, т.е. имеет решение (причем единственное), если определитель основной матрицы не равен 0.
I. Крамер – метод решения системы.
Он заключается в использовании для записи решения формул  где
где 
 заменой соответственно первого, второго и 3-го столбцов и свободных коэффициентов.
заменой соответственно первого, второго и 3-го столбцов и свободных коэффициентов.
Ответ: 
Например, разрешим систему:


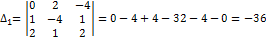



Ответ: 
Сложение векторов
Суммой двух векторов  и
и  называется вектор
называется вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец – с концом вектора
, а конец – с концом вектора  , отложенного из конца вектора
, отложенного из конца вектора  (правило треугольника).
(правило треугольника).

Суммой векторов  и
и  называется такой третий вектор
называется такой третий вектор  , что при совмещенных началах этих трех векторов, векторы
, что при совмещенных началах этих трех векторов, векторы  и
и  служат сторонами параллелограмма, а вектор
служат сторонами параллелограмма, а вектор  – его диагональю (называется сложением по правилу параллелограмма).
– его диагональю (называется сложением по правилу параллелограмма).

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

При сложении векторов выполняется переместительныйзакон, т.е. 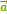 +
+  =
=  +
+ 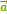
и сочетательныйзакон, т.е. (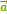 +
+  )+
)+  =
= 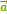 +(
+( +
+  )
)
Вычитание векторов
Под разностью векторов  и
и  понимается вектор
понимается вектор 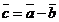 такой, что
такой, что  (см. рис. 5).
(см. рис. 5).
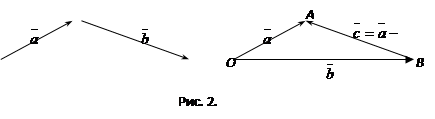
Умножение вектора на число
Произведением вектора 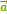 на число k называется такой вектор
на число k называется такой вектор  , длина которого равна |k|⋅|
, длина которого равна |k|⋅| 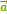 |, причем векторы сонаправлены, если k>0, и противоположно направлены, если k<0.
|, причем векторы сонаправлены, если k>0, и противоположно направлены, если k<0.
Произведение нулевого вектора на любое число есть нулевой вектор.
Обозначение 
Вектора 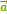 и
и  коллинеарны для любого k. Если два вектора
коллинеарны для любого k. Если два вектора 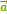 и
и  коллинеарны – то существует такое число k, что
коллинеарны – то существует такое число k, что 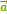 =k
=k  .
.
Произведение любого вектора на число нуль есть нулевой вектор.
Для любых векторов 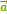 и
и  и чисел k и l справедливы следующие законы:
и чисел k и l справедливы следующие законы:
Сочетательный: (kl)a→=k(l 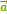 )
)
Первый распределительный: k( 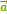 +
+  )=k
)=k 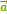 +k
+k 
Второй распределительный: (k+l) 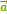 =k
=k 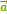 +l
+l 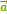
Разложение вектора по базисным ортам. Направляющие косинусы. Длины векторов. Примеры.
Единичные векторы  выходящие из начала координат в положительных направлениях осей OX, OY и OZ называются ортами этих осей.
выходящие из начала координат в положительных направлениях осей OX, OY и OZ называются ортами этих осей.
Любой вектор  можно разложить по ортам осей координат:
можно разложить по ортам осей координат:  , или
, или
 (на плоскости).
(на плоскости).
Пример:
Задание. Вектор  задан своими координатами:
задан своими координатами:  . Записать разложение данного вектора по ортам осей координат.
. Записать разложение данного вектора по ортам осей координат.
Решение.

Числа  называются направляющими косинусами вектора
называются направляющими косинусами вектора  .
.
Направляющие косинусы вектора  определяются соотношениями:
определяются соотношениями:
 , ясно что
, ясно что 
Пример: а = (3; -6; 2).


Длина вектора называется его модулем и обозначается 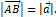
Если 
Если 
Пример: а = (3; -6; 2).

17. Ортогональные, коллинеарные и компланарные векторы: определения и примеры. Условия ортогональности, коллинеарности и компланарности.
Два вектора называются ортогональными, если в пересечении они образуют прямой угол, т.е. угол в 90о.
Два вектора называются коллинеарными, если они лежат на одной прямой либо на параллельных прямых.
Три вектора называются компланарными, если они лежат в одной плоскости либо в параллельных плоскостях.
Условие ортогональности векторов. Два вектора  и
и  ортогональны (перпендикулярны), если их скалярное произведение равно нулю.
ортогональны (перпендикулярны), если их скалярное произведение равно нулю.  ·
·  = 0
= 0
Условия коллинеарности
Ø Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Ø Два вектора коллинеарны, если отношения их координат равны.
Ø Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
Условия компланарности векторов
Ø Три вектора компланарны если их смешанное произведение равно нулю.
Ø Три вектора компланарны если они линейно зависимы.
Ø Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.
(НУЖНЫ ПРИМЕРЫ)
Условия коллинеарности
Ø Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Ø Два вектора коллинеарны, если отношения их координат равны.
Ø Два вектора коллинеарны, если их векторное произведение равно нулевому вектору.
Канон – от греч.в переводе означает типовое, образцовое.
Любой вектор лежащий на прямой l либо на  прямой, называется направляющим вектором l.
прямой, называется направляющим вектором l.
Рассматривается прямая l.
Пусть  фиксированная точка на прямой. М – текущая точка, т.е. произвольная.
фиксированная точка на прямой. М – текущая точка, т.е. произвольная.

Тогда векторы  коллинеарны, а значит их соответствующие координаты должны быть пропорциональны.
коллинеарны, а значит их соответствующие координаты должны быть пропорциональны.

Если  , то
, то 
Если  , то аналогично
, то аналогично 
Матрицы и основные действия над ними. Пример умножения двух матриц.
I. Сложение. Матрицы можно сложить, если у них одинаковые порядки. Если матрица  и матрица
и матрица 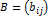 , то
, то 
Например:
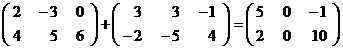 .
.
II. Умножение на число. Если матрица  и
и  – число,то
– число,то  .
.
Например: если число  = 2 и матрица
= 2 и матрица  , то
, то 

III. Умножение матриц. МатрицыА и В можно перемножить, если число столбцов матрицы А совпадает с числом строк матрицы В.
Например, нельзя перемножать две матрицы
 и В =
и В = 
Матрицы умножаются специальным правилом, например,


В общем случае АВ не равно ВА, но если это равенство выполняется, то матрицыА и В называются коммутирующими друг другу.
Матрица А-1 называется обратной матрицей А, если выполняются соотношения:

Выполняются следующие свойства:
(А + В) + С = А + (В + С)

(A-1)-1 = A
(А  В)
В)  С = А
С = А  (В
(В  С)
С)
(А  В)-1 =B-1
В)-1 =B-1  A-1
A-1
3. Элементарные преобразования над матрицами. Эквивалентные матрицы. Приведение матриц к ступенчатому виду, пример.
Под элементарными преобразованиями над матрицей понимают:
1. Вычеркивание 0-го ряда;
2. Замена местами любых двух параллельных рядов;
3. Умножение на ненулевое число.
4. Транспонирование.
5. Умножение любого ряда на число.
6. Прибавление к любому ряду параллельного ряда, умноженное на любое ненулевое число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А ~ В.
С помощью таких преобразований любую матрицу можно привести к ступенчатому (треугольному) виду; более того матрицу можно преобразовать таким образом, что останутся в конечном счете только 0 и 1. Число полученных 1 составляет ранг матрицы.
Пример. Привести матрицу к ступенчатому виду.
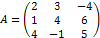
1. Меняем местами 1-ю и 2-ю строки, тогда

2. (-2) умножили на первую строку и прибавили ко 2-й строке; затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.
3. 
 затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.
затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.







4. Вторую строку умножили на (-17/5) и прибавили к 3-ей.





Определители 2-го и 3-го порядка и методы их вычисления. Примеры.
Понятие определителя - число, характеризующее квадратную матрицу  , необходимо для решения систем линейных алгебраических уравнений.
, необходимо для решения систем линейных алгебраических уравнений.
Определитель матрицы  обозначают
обозначают  ,
,  ,
,  .
.
1) Определителем матицы 1-го порядка 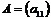 , называется элемент
, называется элемент 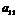 :
:  ;
;
2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
 . Произведения
. Произведения  называются членами определителя 2-го порядка.
называются членами определителя 2-го порядка.
Примеры:
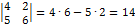

3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
 .
.
Данная формула получила название правила треугольников или правило Саррюса. Оно символически записывается так:

 .
.
Примеры: Вычислить определитель матрицы
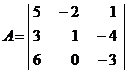 .
.
Решение: 

 .
.
Определители 2-го и 3-го порядка и их основные свойства.
Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:
 . Произведения
. Произведения  называются членами определителя 2-го порядка.
называются членами определителя 2-го порядка.
Пример. Вычислить определитель матрицы  . Р е ш е н и е.
. Р е ш е н и е.  .
.
3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:
 .
.
Данная формула получила название правила треугольников или правило Саррюса. Оно символически записывается так:

 .
.
Основные свойства определителей:
1. Если любой ряд состоит из 0, то определитель равен 0.
2. Если любые 2 параллельных ряда одинаковы или пропорциональны, то определитель равен 0.
3. Если поменять местами любые 2 параллельных ряда, то определитель изменит знак.
4. Определитель не изменится при транспортировании.
5. Общий множитель любого ряда можно вынести за знак 
6. К любому ряду можно прибавить параллельный ряд, умноженный на ненулевое число, причем определитель не изменится.
7. Миноры и алгебраические дополнения элементов определителя. Разложение определителя по элементам строки и столбца, примеры. Понятие ранга матрицы.
Минором элемента  матрицы А =
матрицы А =  называется определитель, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается
называется определитель, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается 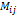 .
.
Алгебраическим дополнением элемента  определителя называется его минор, взятый со знаком «плюс», если сумма
определителя называется его минор, взятый со знаком «плюс», если сумма  – четное число, и со знаком «минус», если эта сумма нечетная. Обозначается
– четное число, и со знаком «минус», если эта сумма нечетная. Обозначается  .
.
Пример: Найти минор и алгебраические дополнения 2-х элементов матрицы:

Решение:
Имеем: 

Имеем: 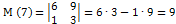

Любой определитель можно разложить по элементам любой строки или любого столбца:

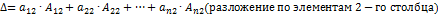 .
.
Определитель 3-го порядка вычисляется методом треугольников Саррюса.
Пример:

2 способ:

 .
.
Рангом матрицы А называется наибольший порядок ≠ 0 минору элементов этой матрицы. По другому, ранг – это число линейно-независимых строк или столбцов данной матрицы.
11. Система двух линейных неоднородных уравнений от двух неизвестных: определение и методы Крамера и Гаусса решения. Пример. ( составила сама, ибо не правильно, я не виновата)
К такой относится система вида

Здесь  коэффициенты.
коэффициенты.
Если хотя бы один свободный коэффициент не равен 0, то система называется неоднородной, если же 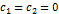 – однородной. Однородная система обозначается символом
– однородной. Однородная система обозначается символом 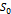 и всегда имеет решение (хотя бы нулевое).
и всегда имеет решение (хотя бы нулевое).
Неоднородная система совместна, т.е. имеет решение (причем единственное), если определитель основной матрицы не равен 0.
I. Крамер – метод решения системы.
Он заключается в использовании для записи решения формул 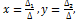 где
где 
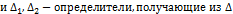 заменой соответственно первого и второго столбцов и свободных коэффициентов.
заменой соответственно первого и второго столбцов и свободных коэффициентов.
Здесь 
II. Метод Гаусса. Он заключается в последовательном исключении неизвестных системы путем элементарных преобразований, в результате чего система приводится к ступенчатому виду, после чего выписывается решение.
Например, разрешим систему:





Ответ: 
НУЖЕН ПРИМЕР Гаусса
Система трех линейных неоднородных алгебраических уравнений: определение и метод Крамера решения. Пример.
К такой относится система вида

Здесь 
Если хотя бы один свободный коэффициент не равен 0, то система называется неоднородной, если же  – однородной. Однородная система обозначается символом
– однородной. Однородная система обозначается символом 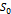 и всегда имеет решение (хотя бы нулевое).
и всегда имеет решение (хотя бы нулевое).
Неоднородная система совместна, т.е. имеет решение (причем единственное), если определитель основной матрицы не равен 0.
I. Крамер – метод решения системы.
Он заключается в использовании для записи решения формул  где
где 
 заменой соответственно первого, второго и 3-го столбцов и свободных коэффициентов.
заменой соответственно первого, второго и 3-го столбцов и свободных коэффициентов.
Ответ: 
Например, разрешим систему:


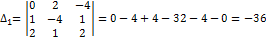



Ответ: 



 и матрица
и матрица 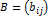 , то
, то 
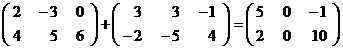 .
. – число,то
– число,то  .
. , то
, то 





 В)
В) 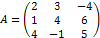


 затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.
затем 1-ю строку умножили на (-4) и прибавили к 3-й строке.









 , необходимо для решения систем линейных алгебраических уравнений.
, необходимо для решения систем линейных алгебраических уравнений. ,
,  ,
,  .
.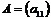 , называется элемент
, называется элемент 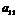 :
:  ;
; . Произведения
. Произведения  называются членами определителя 2-го порядка.
называются членами определителя 2-го порядка.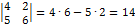

 .
.
 .
.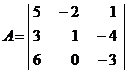 .
.

 .
.

 – однородной. Однородная система обозначается символом
– однородной. Однородная система обозначается символом 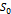 и всегда имеет решение (хотя бы нулевое).
и всегда имеет решение (хотя бы нулевое). где
где 
 заменой соответственно первого, второго и 3-го столбцов и свободных коэффициентов.
заменой соответственно первого, второго и 3-го столбцов и свободных коэффициентов.


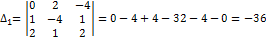




 и
и  называется вектор
называется вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 
 и
и  , что при совмещенных началах этих трех векторов, векторы
, что при совмещенных началах этих трех векторов, векторы 

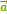 +
+  =
=  =
=  и
и  понимается вектор
понимается вектор 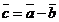 такой, что
такой, что  (см. рис. 5).
(см. рис. 5).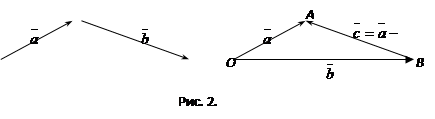

 коллинеарны для любого k. Если два вектора
коллинеарны для любого k. Если два вектора  выходящие из начала координат в положительных направлениях осей OX, OY и OZ называются ортами этих осей.
выходящие из начала координат в положительных направлениях осей OX, OY и OZ называются ортами этих осей. можно разложить по ортам осей координат:
можно разложить по ортам осей координат:  , или
, или (на плоскости).
(на плоскости). задан своими координатами:
задан своими координатами:  . Записать разложение данного вектора по ортам осей координат.
. Записать разложение данного вектора по ортам осей координат.
 называются направляющими косинусами вектора
называются направляющими косинусами вектора  , ясно что
, ясно что 


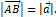


 ортогональны (перпендикулярны), если их скалярное произведение равно нулю.
ортогональны (перпендикулярны), если их скалярное произведение равно нулю.  прямой, называется направляющим вектором l.
прямой, называется направляющим вектором l. фиксированная точка на прямой. М – текущая точка, т.е. произвольная.
фиксированная точка на прямой. М – текущая точка, т.е. произвольная.

 коллинеарны, а значит их соответствующие координаты должны быть пропорциональны.
коллинеарны, а значит их соответствующие координаты должны быть пропорциональны.
 , то
, то 
 , то аналогично
, то аналогично 
 . Р е ш е н и е.
. Р е ш е н и е.  .
. .
.

 матрицы А =
матрицы А =  называется определитель, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается
называется определитель, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается 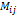 .
. – четное число, и со знаком «минус», если эта сумма нечетная. Обозначается
– четное число, и со знаком «минус», если эта сумма нечетная. Обозначается  .
.


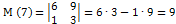


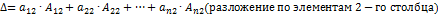 .
.

 .
.
 коэффициенты.
коэффициенты.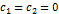 – однородной. Однородная система обозначается символом
– однородной. Однородная система обозначается символом 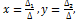 где
где 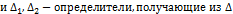 заменой соответственно первого и второго столбцов и свободных коэффициентов.
заменой соответственно первого и второго столбцов и свободных коэффициентов.







