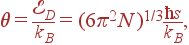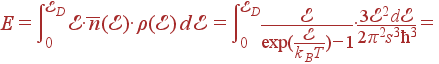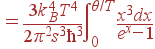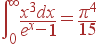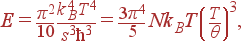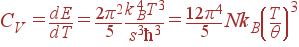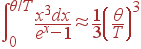Колебания кристаллической решетки
Кристаллическая структура — равновесное состояние системы атомов, отвечающее минимуму потенциальной энергии. В состоянии покоя сумма сил, действующих на каждый атом кристалла со стороны других атомов, равна нулю.
Если вывести эту систему из положения равновесия, в кристалле возникнут сложные колебания. Эти колебания, в частности, всегда имеются при конечной температуре, когда кристаллическая структура обладает определенной (тепловой) энергией, т.е. не находится в состоянии статического равновесия.
Рассмотрим колебания решетки в рамках классической механики.
При смещении атома относительно других атомов кристалла возникает сила, стремящаяся вернуть его в равновесное положение. Если смещения невелики, мы можем разложить зависимость силы от смещений в ряд и ограничится линейными по смещениям членами. Тогда колебания кристаллической решетки будут линейными, т. е. будут описываться системой линейных дифференциальных уравнений.
Такая система уравнений обладает важным свойством: если есть несколько решений, то их сумма также является решением, т. е. сумма двух возможных колебаний — тоже колебание.
Эта система может быть решена, если известна зависимость силы, действующей на атом, от его смещения, а основные характеристики линейных колебаний могут быть предсказаны на основании одних только свойств симметрии кристалла.
Чтобы показать главные черты линейных колебаний кристаллической решетки, мы рассмотрим простейший случай одномерного кристалла — одномерную цепочку атомов.
Решение со знаком ''плюс''.
В точке k = 0:
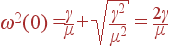
| (37)
|
На границе зоны Бриллюэна:
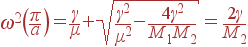
| (38)
|
Групповая скорость этой ветви ∂ ω /∂ k равна нулю как на границе зоны Бриллюэна, так и при k = 0.
Эта ветвь целиком лежит выше акустической ветви: ее минимальная частота 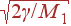 больше максимальной частоты акустических колебаний
больше максимальной частоты акустических колебаний  . Таким образом, в цепочке могут распространяться волны в частотами от 0 до
. Таким образом, в цепочке могут распространяться волны в частотами от 0 до  и от
и от 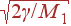 до
до  . Интервал частот
. Интервал частот 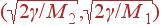 является ''запрещенной зоной'': волн с такими частотами не существует. Относительная ширина этого интервала тем больше, чем больше отношение масс M 2/ M 1.
является ''запрещенной зоной'': волн с такими частотами не существует. Относительная ширина этого интервала тем больше, чем больше отношение масс M 2/ M 1.
Чтобы понять, что представляют собой длинноволновые колебания этой ветви, найдем отношение амплитуд колебаний B / A при k = 0 с помощью (36):
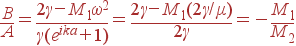
| (39)
|
Мы видим, что атомы в каждой ячейке движутся в противофазе, то сближаясь, то удаляясь друг от друга, причем одновременно во всех ячейках (если k = 0). Амплитуда движения легкого атома больше амплитуды тяжелого в M 2/ M 1 раз, т. е. центр тяжести ячейки остается на месте.
 Рис. 6. Амплитуды атомов цепочки в случае длинноволновых оптических колебаний.
Рис. 6. Амплитуды атомов цепочки в случае длинноволновых оптических колебаний.
|
Если атомы заряжены, то при колебаниях такого типа каждая ячейка представляет собой переменный дипольный момент. Дипольные моменты взаимодействуют с электромагнитным полем, и колебания легко возбуждаются электромагнитными волнами соответствующих частот. В связи с этим, вся ветвь колебаний называется оптической.
При длинноволновых акустических колебаниях атомы ячейки движутся в фазе и никакого дипольного момента не возникает. Поэтому акустические колебания с электромагнитным полем взаимодействуют слабо.
Энергия длинноволнового оптического фонона имеет тот же порядок величины, что и энергия фонона акустического колебания с максимальной частотой, которую мы оценили в 0.05 эВ. Энергии оптических фононов большинства полупроводниковых кристаллов лежат в диапазоне 0.03÷ 0.1 эВ.
Посмотрим теперь, как колеблются атомы, когда длина волны минимальна, т. е. когда волновой вектор лежит на границе зоны Бриллюэна.
В случае акустических колебаний ω 2 = 2 γ / M 2, коэффициент при B во втором уравнении системы (25) обращается в ноль, откуда следует что A = 0.
В случае оптических колебаний ω 2 = 2 γ / M 1, и из первого уравнения (25) следует что B = 0.
Таким образом, при k = π / a в случае акустических волн колеблются тяжелые атомы, а легкие неподвижны, в случае оптических, наоборот: колеблются легкие, тяжелые стоят на месте.
Обобщим теперь полученные результаты. Нетрудно показать, что если примитивная ячейка одномерной цепочки содержит l атомов, то спектр колебаний состоит из l ветвей, одна из которых акустическая, а остальные — оптические.
Мы рассматривали бесконечную цепочку, не накладывая никаких ограничений на длины волн упругих колебаний. В результате, мы пришли к выводу, что в цепочке могут распространяться колебания с любыми волновыми векторами, лежащими в первой зоне Бриллюэна. (Было показано, что из-за дискретности цепочки волновые вектора, отличающиеся на произвольный вектор обратной решетки, описывают одни и те же колебания. Поэтому можно брать волновой вектор из любой зоны Бриллюэна. Естественней всего описывать колебание наименьшим волновым вектором, т. е. вектором из первой зоны Бриллюна.)
Чтобы иметь дело не с непрерывным, а с дискретным набором волновых векторов, можно потребовать, чтобы отклонение атомов от равновесия было периодической функцией: u (xn) = u (xn + L). Иными словами — поставить граничные условия Борна-Кармана. Период L должен быть кратен постоянной решетки цепочки.
Условиям Борна-Кармана удовлетворяют только гармонические колебания с ''разрешенными'' волновыми векторами kn = 2 π n / L. Нетрудно подсчитать, что в зоне Бриллюэна размещается L / a разрешенных волновых векторов, т. е. ровно столько, сколько примитивных ячеек укладывается на длине L. (Волновым векторам – π / a и π / a соответствует одно и то же колебание и поэтому считаем эти два значения за одно). Мы уже упоминали выше об этом свойстве зоны Бриллюэна.
Т. к. колебание однозначно определяется волновым вектором и ветвью, то различных колебаний столько, сколько атомов содержит цепочка. Это общее свойство линейных колебательных систем: количество независимых колебаний (нормальных мод) равно числу степеней свободы системы.
Трехмерный кристалл
Мы рассмотрели колебания в одномерной цепочке. Подобным образом могут быть описаны и колебания решетки трехмерного кристалла.
Предположим, что примитивная ячейка кристалла состоит из l атомов. Каждый атом ячейки будем обозначать индексом s, этот индекс принимает l различных значений. Любой атом кристалла однозначно определяется радиус-вектором 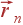 , задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).
, задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).
Смещение атомов при колебаниях решетки является линейной комбинацией плоских гармонических волн (точнее, их вещественных частей):
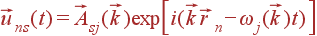
| (40)
|
Частота колебаний одинакова для всех атомов кристалла. Амплитуда колебаний зависит от типа атома (индекса s), т. е. одинакова для всех однотипных атомов. Направление вектора амплитуды может, вообще говоря, быть каким угодно.
Индекс j обозначает ветвь колебаний. Волновой вектор 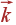 и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости
и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости 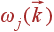 и
и 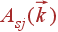 являются непрерывными функциями.
являются непрерывными функциями.
Если примитивная ячейка кристалла содержит l атомов, то число ветвей равно 3 l. Таким образом, каждому значению волнового вектора соответствуют 3 l разных колебаний.
Три из этих ветвей — акустические, в предельном случае длинных волн их частота пропорциональна длине волнового вектора ω = s | k |. Однако скорость звука s зависит от направления распространения волны, т. е. от направления 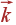 . В случае длинноволновых акустических колебаний амплитуды всех атомов примитивной ячейки примерно одинаковы.
. В случае длинноволновых акустических колебаний амплитуды всех атомов примитивной ячейки примерно одинаковы.
Остальные 3 l –3 ветвей — оптические, при 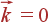 их частота отлична от нуля.
их частота отлична от нуля.
По направлению амплитуды относительно волнового вектора акустические колебания можно разделить на продольное (LA) и два поперечных (TA). Строго говоря, смещения атомов при этих колебаниях параллельны или перпендикулярны вектору 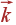 только при распространении волны в направлениях высокой симметрии, например [100] для кристаллов кубической сингонии. Как правило, скорость звука у продольного колебания больше чем у поперечных.
только при распространении волны в направлениях высокой симметрии, например [100] для кристаллов кубической сингонии. Как правило, скорость звука у продольного колебания больше чем у поперечных.
У кристаллов со структурой алмаза или цинковой обманки примитивная ячейка содержит 2 атома. Соответственно, кроме трех акустических, эти кристаллы обладают тремя оптическими ветвями колебаний, из которых также можно выделить продольную (LO) и две поперечных (TO) ветви.
Как и в одномерном случае, волновые вектора, отличающиеся друг от друга на вектор обратной решетки, соответствуют одному и тому же колебанию. По этой причине достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна.
Количество разрешенных волновых векторов в зоне Бриллюэна равно N = V / v 0 — числу примитивных ячеек в нормировочном объеме кристалла V = L 3 (v 0 – объем примитивной ячейки). Действительно, плотность разрешенных волновых векторов в обратном пространстве равна V /(2 π)3, т. е. в объеме обратного пространства Δ 3 k содержится Δ 3 k · V /(2 π)3 разрешенных волновых векторов. Объем зоны Бриллюэна — объем примитивной ячейки обратной решетки — равен (2 π)3/ v 0, и для числа разрешенных состояний получаем (2 π)3/ v 0· V /(2 π)3 = V / v 0 = N.
Число ветвей — 3 l, поэтому полное число колебаний равно 3 lN — утроенному числу атомов кристалла в объеме L 3, т. е. числу степеней свободы механической системы.
Фононы
Колебаниям решетки, согласно квантовой механике, можно сопоставить квазичастицы — фононы. Каждому колебанию соответствует одно состояние фонона с импульсом 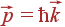 и энергией
и энергией 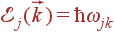 .
.
Фононы являются бозе-частицами: число фононов, соответствующих определенному колебанию (число фононов одном состоянии), может быть сколь угодно большим. В состоянии термодинамического равновесия среднее число фононов njk ветви j с волновым вектором 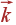 зависит только от энергии фонона (частоты колебания):
зависит только от энергии фонона (частоты колебания):
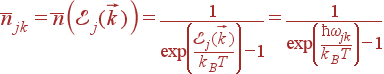
| (41)
|
Здесь kB — постоянная Больцмана. С точки зрения квантовой (да и классической) механики, нормальные колебания решетки ведут себя как набор независимых гармонических осцилляторов. Роль координаты осциллятора играет при этом амплитуда колебания, число фононов является уровнем энергии осциллятора.
На каждое колебание приходится средняя энергия 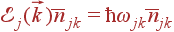 . Строго говоря, к этой энергии надо прибавить энергию основного состояния колебания (энергию нулевых колебаний): как и у обычного гармонического осциллятора она равна
. Строго говоря, к этой энергии надо прибавить энергию основного состояния колебания (энергию нулевых колебаний): как и у обычного гармонического осциллятора она равна  . Но энергией нулевых колебаний кристалл обладает всегда, и мы просто примем ее за начало отсчета.
. Но энергией нулевых колебаний кристалл обладает всегда, и мы просто примем ее за начало отсчета.
При высоких температурах, kb T >> ħ ω, число фононов пропорционально температуре:
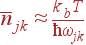
| (42)
|
Средняя энергия колебания при этом равна kbT. Это известный результат классической статистической механики для средней энергии гармонического осциллятора. Таким образом, пока температура превосходит энергию фонона, квантовые эффекты не играют роли.
Они играют существенную роль при низких температурах. Если kb T << ħ ω, то среднее число фононов экспоненциально мало:
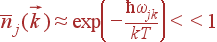
| (43)
|
Можно сказать, что колебания, частота которых превосходит величину kbT /ħ, ''вымерзают''. Энергия колебания не может быть меньше энергии одного фонона ħ ωjk а энергия фонона много больше характерной тепловой энергии kBT, поэтому такие колебания практически не возбуждаются.
Модель Эйнштейна
В модели Эйнштейна предполагается, что частоты всех фононов одинаковы, ωjk = ω 1. Тогда для энергии получаем:
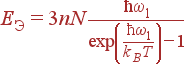
| (47)
|
При высоких температурах, kBT >>ħ ω 1, эта зависимость приводит к выражению (45) для энергии и закону Дюлонга и Пти (46) для теплоемкости.
При низких температурах, kBT <<ħ ω 1, энергия колебаний и теплоемкость экспоненциально уменьшаются:
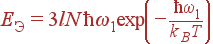
| (48)
|
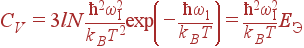
| (49)
|
Модель Эйнштейна хорошо описывает вклад в энергию и теплоемкость оптических ветвей фононов, у которых частота слабо зависит от волнового вектора и ее можно считать постоянной. Чтобы учесть только оптические ветви, частоту которых мы полагаем равной ω 1, нужно вместо 3 l писать число этих ветвей. В общем случае, частоты разных оптических ветвей могут сильно отличаться друг от друга и их вклад в энергию и теплоемкость нужно учитывать отдельно.
Модель Дебая
Опыт показывает, что теплоемкость действительно падает с уменьшением температуры, но не экспоненциально, а пропорционально T 3. Дело в том, что при любых, сколь угодно низких температурах в кристалле найдутся колебания, энергия фонона которых меньше kBT. Это — длинноволновые акустические колебания. Именно такие колебания, точнее те из них, частота которых меньше kBT /ħ, вносят основной вклад в энергию при низких температурах. Колебания с б\'ольшими частотами (оптические и более коротковолновые акустические) ''заморожены'': фононов этих колебаний экспоненциально мало.
Сделаем простую оценку. Вклад в энергию вносят фононы, энергия которых меньше kT. Пусть скорость звука j -й акустической ветви равна sj и не зависит от направления волнового вектора: ω = sj | k |. Тогда вклад в энергию дают колебания с волновыми векторами, меньшими kmax = kBT /(ħ sj). Плотность разрешенных значений волновых векторов в k -пространстве кристалла равна V /(2 π)3, поэтому внутри сферы радиуса kmax содержится
разрешенных значений волновых векторов. Это число колебаний одной акустической ветви, вносящих существенный вклад в энергию. На каждое такое колебание приходится энергия порядка kBT. Для энергии колебаний одной акустической ветви получаем:
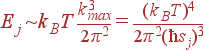
| (50)
|
Т. к. мы вычисляем энергию и теплоемкость единицы объема кристалла, то в (50) мы положили V = 1.
Таким образом, вклад одной акустической ветви в теплоемкость пропорционален T 3:
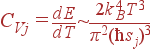
| (51)
|
Чтобы получить полную энергию и теплоемкость, надо сложить вклады от трех акустических ветвей:
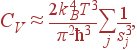
| (52)
|
где через sj обозначена скорости звука j -й акустической ветви.
Мы сделали достаточно грубую оценку, поэтому к численным коэффициентам в последних двух выражениях не стоит относиться серьезно. Тем не менее, эта оценка дает правильную зависимость энергии и теплоемкости от температуры и скорости звука.
Посчитаем теперь энергию решетки при низких температурах более аккуратно.
Формула (44) имеет вид суммы по различным колебаниям (различным состояниям фононов) определенной величины, которая зависит только от энергии фонона:
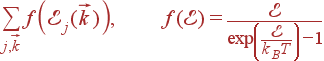
| (53)
|
Такие суммы встречаются довольно часто. Т. к. f зависит только от энергии фонона, то от суммы по состояниям можно перейти к интегралу по энергии:
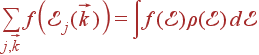
| (54)
|
Здесь 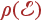 — плотность состояний фононов. Напомним, что
— плотность состояний фононов. Напомним, что 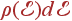 — это число состояний квазичастиц (фононов) в единице объема с энергиями от
— это число состояний квазичастиц (фононов) в единице объема с энергиями от 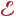 до
до 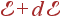 , т. е. число различных колебаний с такими энергиями.
, т. е. число различных колебаний с такими энергиями.
Суммарная плотность состояний складывается из плотности состояний разных ветвей: 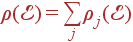 ; плотность состояний ветви определяется ее законом дисперсии
; плотность состояний ветви определяется ее законом дисперсии 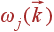 . Аналитически получить законы дисперсии и плотности состояний фононов реальных кристаллов практически невозможно.
. Аналитически получить законы дисперсии и плотности состояний фононов реальных кристаллов практически невозможно.
Однако при низких температурах энергия и теплоемкость определяются длинноволновыми акустическими фононами. Плотность состояний акустических фононов нам известна, мы получили ее в качестве примера, когда вводили само понятие плотности состояний (). Если для j -й акустической ветви ω = sj | k |, то
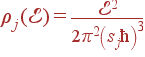
| (55)
|
Плотность состояний длинноволновых колебаний всех акустических ветвей получается суммированием по трем акустическим ветвям:
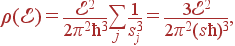
| (56)
|
где s — ''усредненная'' скорость звука:
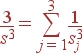
| (57)
|
Линейный закон дисперсии ω = s | k | и соответствующая плотность состояний верны только для малых k. При б\'ольших значениях волнового вектора закон дисперсии и плотность состояний имеют более сложный вид.
Однако при низких температурах вклад в энергию и теплоемкость вносят как раз только длинноволновые фононы, а при высоких температурах вид плотности состояний не важен, т. к. в этом случае на каждое колебание приходится энергия kT. Чтобы получить выражение, которое давало бы правильные предельные зависимости при низких и высоких температурах, Дебай предложил считать, что закон дисперсии ω = s | k | выполняется и при больших k. Максимальное значение волнового вектора kD при этом выбирается так, чтобы в шаре радиуса kD содержалось столько разрешенных значений волновых векторов, сколько их содержится в зоне Бриллюэна, N = 1/ v 0. Иными словами, объем этого шара должен быть равен объему зоны Бриллюэна (2 π)3/ v 0, откуда
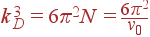
| (58)
|
Таким образом, сохраняя число акустических колебаний, мы заменяем первую зону Бриллюэна сферой, а реальный закон дисперсии — линейным. Фонон с волновым вектором kD имеет энергию 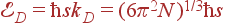 . Соответствующая
. Соответствующая 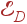 температура,
температура,
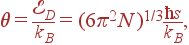
| (59)
|
называется температурой Дебая.
В таком приближении мы можем вычислить вклад акустических ветвей в энергию и теплоемкость решетки:
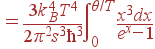
| (60)
|
При низких температурах, T << θ, верхний предел интеграла много больше единицы. Благодаря экспоненте в знаменателе интеграл сходится очень быстро, что позволяет положить верхний предел равным бесконечности. Значение такого интеграла известно:
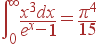
| (61)
|
Для энергии акустических колебаний при низких температурах получаем:
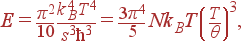
| (62)
|
откуда следует, что теплоемкость решетки при низких температурах пропорциональна T 3:
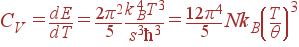
| (63)
|
При высоких температурах, T >> θ, верхний предел интегрирования мал, поэтому можно считать, что exp(x)–1≈ x, таким образом:
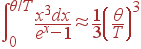
| (64)
|
Это закон Дюлонга и Пти, только вместо полного числа колебаний 3 lN стоит число колебаний акустических ветвей 3 N. (При высоких температурах на каждое колебание приходится средняя энергия kBT, полное число акустических колебаний равно 3 N, поэтому вклад акустических ветвей в энергию равен 3 NkT).
В пределе низких и высоких температур модель Дебая дает точные значения для вклада акустических ветвей в энергию и теплоемкость. В области же промежуточных температур, T ~ θ, эта модель лишь аппроксимирует реальную зависимость энергии и теплоемкости от температуры.
Температура Дебая разделяет две температурные области. В области низких температур на энергию и теплоемкость решетки сильное влияние оказывают квантовые эффекты (''вымерзание'' высокочастотных колебаний). В области высоких температур эти эффекты не существенны, и теплоемкость может быть вычислена в классическом приближении. Для большинства кристаллов температура Дебая лежит в интервале от 100 до 300 K.
Чтобы получить полную энергию и теплоемкость кристаллической решетки, надо к вкладу акустических колебаний прибавить вклад оптических ветвей, для которого хорошим приближением является модель Эйнштейна. Этот вклад пренебрежимо мал при низких температурах. При высоких температурах вклады всех ветвей в энергию и теплоемкость равны.
Колебания кристаллической решетки
Кристаллическая структура — равновесное состояние системы атомов, отвечающее минимуму потенциальной энергии. В состоянии покоя сумма сил, действующих на каждый атом кристалла со стороны других атомов, равна нулю.
Если вывести эту систему из положения равновесия, в кристалле возникнут сложные колебания. Эти колебания, в частности, всегда имеются при конечной температуре, когда кристаллическая структура обладает определенной (тепловой) энергией, т.е. не находится в состоянии статического равновесия.
Рассмотрим колебания решетки в рамках классической механики.
При смещении атома относительно других атомов кристалла возникает сила, стремящаяся вернуть его в равновесное положение. Если смещения невелики, мы можем разложить зависимость силы от смещений в ряд и ограничится линейными по смещениям членами. Тогда колебания кристаллической решетки будут линейными, т. е. будут описываться системой линейных дифференциальных уравнений.
Такая система уравнений обладает важным свойством: если есть несколько решений, то их сумма также является решением, т. е. сумма двух возможных колебаний — тоже колебание.
Эта система может быть решена, если известна зависимость силы, действующей на атом, от его смещения, а основные характеристики линейных колебаний могут быть предсказаны на основании одних только свойств симметрии кристалла.
Чтобы показать главные черты линейных колебаний кристаллической решетки, мы рассмотрим простейший случай одномерного кристалла — одномерную цепочку атомов.



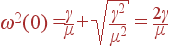
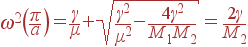
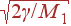 больше максимальной частоты акустических колебаний
больше максимальной частоты акустических колебаний  . Таким образом, в цепочке могут распространяться волны в частотами от 0 до
. Таким образом, в цепочке могут распространяться волны в частотами от 0 до  . Интервал частот
. Интервал частот 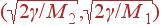 является ''запрещенной зоной'': волн с такими частотами не существует. Относительная ширина этого интервала тем больше, чем больше отношение масс M 2/ M 1.
является ''запрещенной зоной'': волн с такими частотами не существует. Относительная ширина этого интервала тем больше, чем больше отношение масс M 2/ M 1.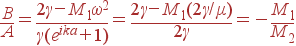
 Рис. 6. Амплитуды атомов цепочки в случае длинноволновых оптических колебаний.
Рис. 6. Амплитуды атомов цепочки в случае длинноволновых оптических колебаний.
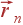 , задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).
, задающим положение ячейки (соответствующего узла решетки Браве), и индексом s, характеризующим положение атома внутри ячейки (тип атома).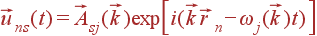
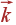 и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости
и ветвь j однозначно определяют частоту и относительные амплитуды атомов всех типов. Для каждой ветви зависимости 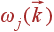 и
и 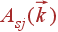 являются непрерывными функциями.
являются непрерывными функциями.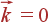 их частота отлична от нуля.
их частота отлична от нуля.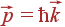 и энергией
и энергией 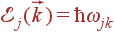 .
.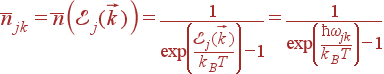
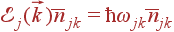 . Строго говоря, к этой энергии надо прибавить энергию основного состояния колебания (энергию нулевых колебаний): как и у обычного гармонического осциллятора она равна
. Строго говоря, к этой энергии надо прибавить энергию основного состояния колебания (энергию нулевых колебаний): как и у обычного гармонического осциллятора она равна  . Но энергией нулевых колебаний кристалл обладает всегда, и мы просто примем ее за начало отсчета.
. Но энергией нулевых колебаний кристалл обладает всегда, и мы просто примем ее за начало отсчета.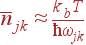
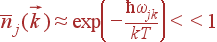
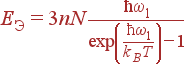
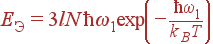
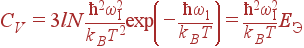
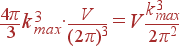
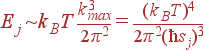
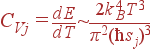
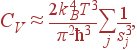
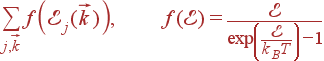
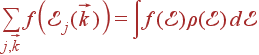
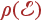 — плотность состояний фононов. Напомним, что
— плотность состояний фононов. Напомним, что 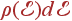 — это число состояний квазичастиц (фононов) в единице объема с энергиями от
— это число состояний квазичастиц (фононов) в единице объема с энергиями от 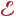 до
до 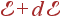 , т. е. число различных колебаний с такими энергиями.
, т. е. число различных колебаний с такими энергиями.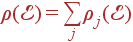 ; плотность состояний ветви определяется ее законом дисперсии
; плотность состояний ветви определяется ее законом дисперсии 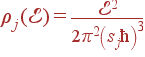
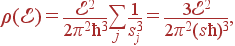
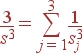
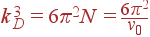
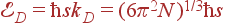 . Соответствующая
. Соответствующая 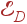 температура,
температура,