СОДЕРЖАНИЕ
Лабораторная работа 1. Экспериментальная проверка
принципа независимости действия сил…………………………………4
Лабораторная работа 2. Испытания на растяжение
металлических образцов…………………………………………………9
Лабораторная работа 3. Определение перемещений
при изгибе балки………………………………………………………...19
Лабораторная работа 4. Определение модуля продольной
упругости для стали……………………………………………………..24
Лабораторная работа 5. Составление кинематической схемы
и структурный анализ рычажных механизмов………………………..27
Лабораторная работа 6. Определение механического КПД
винтовой пары…………………………………………………………...33
Лабораторная работа 7. Определение момента трения
в подшипниках качения……………………………………………...…39
Лабораторная работа 8. Определение механического КПД
редуктора с цилиндрическими прямозубыми колесами……………...45
Лабораторная работа 9. Определение характеристик
винтовых пружин сжатия и растяжения……………………………….51
БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………………….…59
Лабораторная работа 1
ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ПРИНЦИПА
НЕЗАВИСИМОСТИ ДЕЙСТВИЯ СИЛ
1. ЦЕЛЬ РАБОТЫ
Ознакомление с оборудованием, приборами и методом экспериментальной проверки принципа независимости действия сил.
2. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
2.1. Принцип независимости действия сил
Принцип независимости действия сил, или принцип суперпозиции, является следствием трех допущений, которые с достаточной степенью точности для практических целей описывают поведение реальных объектов:
а) допущение об идеальной упругости материалов, согласно которому предполагается, что материал обладает способностью восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию;
б) допущение о линейной зависимости между напряжениями и деформациями, т.е. о справедливости закона Гука;
в) допущение о малости перемещений по сравнению с геометрическими размерами элементов конструкций, т.е. не учитываются изменения геометрических размеров элементов и местоположения нагрузок из-за искривления, растяжения, сжатия и сдвига после приложения к ним внешних сил.
В соответствии с этим принципом результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке.
Предположим, что к балке (рис. 1, а) в точке 1 приложена сила F 1, которая вызовет перемещение произвольной точки 3 по направлению силы F 1 (согласно допущению о линейной зависимости между напряжением и деформацией или силой и перемещением)
 (1)
(1)
где  - коэффициент пропорциональности.
- коэффициент пропорциональности.
Первый индекс в обозначении прогиба (перемещения) U соответствует точке, в которой он определяется, второй – показывает, действием какой силы он вызван.
 а) а в
а) а в
 F 1 U 31
F 1 U 31
1 3 2
l
б)
 U 32 F 2
U 32 F 2
в)
 F 1 U 3(1,2) F 2
F 1 U 3(1,2) F 2
Рис. 1. Расчетная схема балки
Снимем силу F 1 и приложим в некоторой точке 2 силу F 2 (рис. 1, б), которая вызовет перемещение точки 3 на величину
 (2)
(2)
Коэффициенты пропорциональности  и
и  будут различны, поскольку силы F 1 и F 2 приложены в разных точках.
будут различны, поскольку силы F 1 и F 2 приложены в разных точках.
Рассмотрим совместное действие сил F 1 и F 2, для чего сначала приложим в точке 1 силу F 1, а затем силу F 2 (рис. 1, в). Точка 3 получит перемещение:
 (3)
(3)
Коэффициент  будет тот же, что и в формуле (1), т.к. сила F 1 прикладывалась первой. Коэффициент
будет тот же, что и в формуле (1), т.к. сила F 1 прикладывалась первой. Коэффициент  , в отличие от
, в отличие от  , в формуле (2) помечен штрихом, т.к. сила F 2 прикладывалась не к свободной системе, что имело место при определении U 32 по формуле (2), а к предварительно нагруженной системе силой F 1.
, в формуле (2) помечен штрихом, т.к. сила F 2 прикладывалась не к свободной системе, что имело место при определении U 32 по формуле (2), а к предварительно нагруженной системе силой F 1.
Если коэффициенты  и
и  различны, то следует, что
различны, то следует, что  зависит от F 1. Но это противоречит принятому предположению о линейной зависимости перемещения от действующих сил. Следовательно,
зависит от F 1. Но это противоречит принятому предположению о линейной зависимости перемещения от действующих сил. Следовательно,  и тогда
и тогда
 (4)
(4)
т.е. перемещение точки 3 от действия сил F 1 и F 2 равно сумме перемещений точки 3, вызванных силами F 1 и F 2 в отдельности.
Если изменить порядок приложения сил, то можно путем аналогичных рассуждений прийти к тому же выражению (4), т.е. результат действия сил не зависит от порядка их приложения.
Это положение легко обобщается и на случай любого числа сил и для различных результатов, например угловых перемещений.
Принцип независимости действия сил является основным руководящим правилом при решении большинства задач сопротивления материалов.
3. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
Опытная проверка принципа независимости действия сил может быть проведена на установке для исследования двухопорной балки типа СМ4А (рис. 2).
Установка состоит из следующих основных частей: балки 1 – стальной полосы с сечением 7х40 мм, основания 2, подвижной 3 и неподвижной 4 стоек, индикаторной стойки 5, двух гиревых подвесок и набора грузов (на рис. 2 не показаны). Подвижная стойка 3 имеет возможность перемещаться по направляющей планке 6, что позволяет регулировать длину пролета в пределах от 700 до 1000 мм.
Нагружение балки осуществляется с помощью подвесок и набора грузов. Нагрузка прикладывается сосредоточенно. При этом имеется возможность изменять точку приложения нагрузки.
Измерение прогибов (перемещение точек балок) производится с помощью индикатора часового типа 7 с ценой деления 0,01 мм. Индикатор для измерения прогиба закреплен в индикаторной стойке, которая может перемещаться вдоль основания установки по направляющей 6. Фиксация осуществляется с помощью стопора.





























 7 5 6 4
7 5 6 4
Рис. 2. Экспериментальная установка СМ4А
4. ПОРЯДОК ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
1. Согласно указанной преподавателем схеме нагружения подготовить установку для проведения опыта, определив положения точек 1,2 и 3 на балке 1 (см. рис. 1 и 2).
2. Установить с помощью индикаторной стойки в точке 3 индикатор таким образом, чтобы стрелка на малой шкале стояли на 9 или 10 мм. Вращением подвижной шкалы индикатора установить точно нулевое положение индикатора.
3. Нагрузить балку в точке 1 нагрузкой F 1.
4. По показаниям индикатора определить величину прогиба (перемещения) U 31 точки 3.
Повторить четыре раза при значениях F 1=20, 30, 40, 50 Н.
Данные записать в таблицу.
5. Разгрузить балку. Установить нулевое показание индикатора.
6. Нагрузить балку в точке 2 нагрузкой F 2.
7. По показаниям индикатора определить величину прогиба U 32 балки в точке 3.
Повторить четыре раза при значениях F 2=20, 30, 40, 50 Н.
Данные записать в таблицу.
| №
п/п
| F1,
H
| U31,
мм
| F2,
H
| U32,
мм
| F1+F2,
H
| U3(1,2),
мм
| U31+U32,
мм
| dU3,
%
|
|
|
|
|
|
| 20+20
|
|
|
|
|
|
|
|
|
| 30+30
|
|
|
|
|
|
|
|
|
| 40+40
|
|
|
|
|
|
|
|
|
| 50+50
|
|
|
|
8. Разгрузить балку. Установить нулевое показание индикатора.
9. Нагрузить балку в точке 1 силой F 1, в точке 2 - силой F 2 (можно F 1= F 2).
10. По индикатору определить прогиб U 3(1,2).
Повторить четыре раза, принимая F 1= F 2=20, 30, 40, 50 Н.
Данные записать в таблицу.
11. Провести проверку принципа независимости действия сил, используя формулу (4), для чего определить отклонение для каждого значения нагрузки F
 (5)
(5)
затем найти среднее значение
 (6)
(6)
Результаты опыта считаются удовлетворительными, если 
5. СОСТАВЛЕНИЕ ОТЧЕТА
В отчете о проделанной работе должно быть: наименование и цель работы, формулировка принципа независимости действия сил; расчетная схема балки с указанием мест установки подвесок с грузами, таблицы заданных значений нагрузок и полученных перемещений точек балки и результатов вычислений.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. На каких допущениях базируется принцип независимости действия сил?
2. Объяснить допущение об идеальной упругости материалов.
3. Объяснить допущение о малости перемещений по сравнению с геометрическими размерами элементов конструкций.
4. Сформулируйте принцип независимости действия сил.
5. Дать краткое описание установки СМ4А.
6. Что понимают под результатом воздействия силы?
7. Рассказать о порядке проведения лабораторной работы.
Лабораторная работа 2
Рис. 1. Диаграмма растяжения
Если растянутый образец, имеющий напряжение  , постепенно разгрузить, то диаграмма разгрузки совпадет с начальным участком нагружения ОВ, т.е. в материале развивались только упругие деформации.
, постепенно разгрузить, то диаграмма разгрузки совпадет с начальным участком нагружения ОВ, т.е. в материале развивались только упругие деформации.
Максимальное напряжение, до которого в материале появляются только упругие деформации, называется пределом упругости sу. Предел упругости подавляющего большинства материалов практически совпадает с пределом пропорциональности и поэтому их обычно считают одинаковыми.
Понятия предел пропорциональности и предел упругости довольно условны. Поэтому величины sn и sу в справочные данные по свойствам материалов обычно не включаются.
При дальнейшем нагружении образца диаграмма искривляется и, начиная с некоторой т. С, становится горизонтальной (или почти горизонтальной). При этом относительные деформации растут без увеличения напряжений, т.е. происходит явление, называемое текучестью материала. Участок СД диаграммы называется площадкой текучести. Напряжение, при котором деформации растут без увеличения нагрузки, называется пределом текучести s т.
У некоторых материалов, например, сплавы алюминия, чугуна меди на диаграмме растяжения нет площадки текучести. Для этих материалов вводиться понятие так называемого условного предела текучести s 0,2, равного напряжению, при котором остаточные деформации составляют 0,2%. Для определения s 0,2 необходимо отложить на оси абсцисс диаграммы  отрезок (рис. 2)
отрезок (рис. 2)
 (2)
(2)
 F
F


 B
B
 A
A
F0,2
B1 


 O
O


Рис. 2. Диаграмма растяжения без площадки текучести
Из т. В 1 провести прямую, параллельную ОА до пересечения с кривой в т. В. Ордината т. В соответствует нагрузке F 0,2. Тогда
 (3)
(3)
Текучесть происходит за счет роста пластической (неупругой) деформации материала. Внешним проявлением возникновения пластических деформаций материала является помутнение полированной поверхности образца, появление на ней так называемых линий Чернова-Людерса, расположенных примерно под углом 450 к оси образца. Эти линии практически совпадающие с плоскостями наибольших касательных напряжений, представляют собой следы происшедших остаточных деформаций сдвига. Явление текучести связано с изменением внутренней структуры металлов.
После окончания процесса перестройки внутренней структуры, природа которого еще недостаточно изучена, металл приобретает способность вновь сопротивляться действующей нагрузке.
После площадки текучести нагрузка вновь увеличивается, т.е. происходит так называемое явление упрочнения металла. Между напряжением и деформацией устанавливается сложная криволинейная зависимость (участок DL). Напряжение в высшей точке L диаграммы носит название предела прочности sв или временного сопротивления. Пределом прочности называется отношение наибольшей растягивающей силы, которую выдерживает образец, к первоначальной площади поперечного сечения А 0, т.е.
 (4)
(4)
Следовательно, предел прочности sв является условной величиной, которая меньше истинного напряжения прочности, т.к. к этому моменту деформирования образца его действительная площадь сечения меньше первоначальной.
После достижения предела прочности характер относительных продольных удлинений изменяется. Они концентрируются в одном месте на небольшой длине, где происходит местное сужение образца и образуется так называемая шейка (рис. 3), в пределах которой затем происходит разрыв образца.
 Шейка
Шейка

Рис. 3. Местное сужение образца
Уменьшение площади поперечного сечения в шейке влечет за собой падение нагрузки. Диаграмма от т. L до разрыва образца описывается ниспадающей кривой LM. В точке М происходит разрушение образца при условном напряжении sраз разрыва. Величины sn, sу, sт и sв характеризуют способность материала сопротивляться стремлению внешних сил деформировать и разрушать образец и называются характеристиками прочности материала.
Истинная диаграмма растяжения (пунктирная линия) строится по напряжениям, определяемым по формуле
 (5)
(5)
где Аист – действительное значение площади поперечного сечения образца в момент нагрузки F.
Если, начиная с некоторой точки Т диаграммы (см. рис. 1), разгрузить образец, то диаграмма пойдет по прямой ТТ 2, приблизительно параллельной прямой ОА. Отрезок ОТ 2 равен остаточной деформации eост, соответствующей точке Т, а отрезок Т 1 Т 2 – упругой деформации eуп. Полная деформация
 (6)
(6)
Если теперь вновь нагружать образец, то диаграмма пойдет примерно по линии Т 2 mТ, образуя небольшую петлю (на рис. 1 заштрихована), которая получается вследствие необратимых потерь энергии деформации и называется петлей гистерезиса. Начиная с точки Т, диаграмма пойдет так, как будто не было разгрузки и повторной нагрузки образца. Это показывает, что при нагружении образца выше предела текучести и последующей его разгруке металл образца изменил свои свойства: пропала площадка текучести, повысился предел пропорциональности и уменьшилась полная деформация при разрыве (Т 2 М 2< ОМ 2) – металл стал как бы боле хрупким. Такое изменение свойства металла называется наклепом.
Растяжение образца сопровождается его нагреванием и намагничиванием. Эти явления особо заметны около места разрыва. После испытания определяют относительное остаточное удлинение образца после разрыва
 (7)
(7)
и относительное остаточное уменьшение площади поперечного сечения в шейке после разрыва
 (8)
(8)
где Ар – площадь поперечного сечения шейки образца, lр – длина образца после разрыва.
Полное относительное остаточное удлинение d и относительное уменьшение поперечного сечения при разрыве y называют характеристиками пластичности материала.
2.2. Форма и размеры образцов
Результаты испытания на растяжение зависят не только от свойств материалов, но и от формы и размеров испытуемых образцов. Для получения сравнимых результатов, получаемых различными лабораториями, установлены типы и размеры образцов.
Стандартные образцы круглого и прямоугольного поперечных сечений изображены на рис. 4. Круглые образцы диаметром d 0=20 мм называют нормальными, а образцы с меньшими (иногда большими) диаметрами или некруглого поперечного сечения – пропорциональными. Наиболее часто применяют цилиндрические образцы, у которых длина l 0 (на образце отмечается рисками), равные десяти диаметрам d 0 (длинные образцы), и образцы с расчетной длиной l 0=5 d 0 (короткие образцы).




 l
l




 d0
d0
l0=10d0



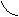

 l
l




 A0
A0


 l0=11,3
l0=11,3 
Рис. 4. Образцы для испытания на растяжение
Чтобы результаты испытаний образцов с различной формой поперечного сечения были сопоставимыми, необходимо обеспечить постоянное отношение расчетной длины образца к квадратному корню из площади поперечного сечения

 (9)
(9)
Таким образом, для длинных образцов
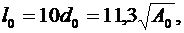 (10)
(10)
для коротких
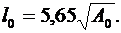 (11)
(11)
3. ПОРЯДОК ПРОВЕДЕНИЯ ИСПЫТАНИЯ
1. Перед испытанием ознакомиться с устройством машины, в журнале наблюдений записать тип машины, цену деления силоизмерительного устройства, масштабы записи диаграммы по нагрузке МF и деформации Мl.
2. Измерить диаметр d 0 образца и определить расчетную длину l 0. Отметить рисками на образце длину l 0.
3. Закрепить образец в захватах машины.
4. Закрепить бумагу на барабан диаграммного аппарата, проверить его работу для чего повернуть барабан в холостую и получить нулевую линию.
5. Включить электродвигатель Р-10 и наблюдать за процессом растяжения образца.
6. После разрушения образца выключить электродвигатель и вынуть из захватов машины обе части образца.
7. Записать значение наибольшей нагрузки Fв по шкале силоизмерительного устройства, снять с барабана бумагу с диаграммой растяжения образца и приступить к обработке результатов испытания.
4. ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ
1. Обе части разрушенного образца сложить вместе и замерить расстояние lр между рисками и диаметр dр образца в месте разрыва.
2. Нанести на полученную диаграмму координатные оси (рис. 5). Ось абсцисс (ось удлинения) совместить с нулевой линией диаграммы, а для проведения оси ординат (оси нагрузки) определить начало координат – точку О. Для этого необходимо продлить прямолинейный участок диаграммы (участок упругих деформаций) до пересечения с осью абсцисс. Таким образом, из рассмотрения исключается криволинейный участок диаграммы, который возникает вследствие первоначального обмятия головок образца в захватах машины.



 F L
F L


 MF M
MF M


 D
D
A
yL
yD
 yA
yA
M2 M1 Δ l




 O Δ l Δ lуп Мl
O Δ l Δ lуп Мl
Рис. 5. Экспериментально полученная программа растяжения
3. Отметить на диаграмме характерные точки А, Д, L и М. Из точки М провести линию ММ 2 параллельно прямолинейному участку диаграммы. Эта линия пересекает на оси абсцисс отрезок ОМ 2, равный величине остаточного удлинения образца в масштабе Мl записи диаграммы.
4. Определить нагрузки, соответствующие точкам А, Д и пределам:
а) пропорциональности
 (12)
(12)
б) текучести
 (13)
(13)
в) прочности
 (14)
(14)
5. Определить характеристики прочности материала:


 (15)
(15)
6. Определить характеристики пластичности материала:
а) относительное остаточное удлинение по формуле (7);
б) относительное остаточное сужение по формуле (8).
7. В случае отсутствия площадки текучести определить величину нагрузки F 0,2 (см. рис. 4), для чего на оси абсцисс диаграммы растяжения отложить отрезок

и провести ВВ/ОА. Ордината уВ точки В определяет в масштабе МF нагрузку F 0,2:

По формуле (3) найти условный предел текучести s 0,2.
5. СОСТАВЛЕНИЕ ОТЧЕТА
Отчет о проделанной работе содержит: наименование, цель и порядок проведения работы, эскиз образца до испытания и после разрушения, его материал, диаграмму растяжения, вычерченную в масштабе, с указанием всех характерных точек и масштабов МF и Мl, вычисления основных механических характеристик материала.
6. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Цель работы.
2. Какие механические характеристики определяют прочность материала?
3. По каким механическим характеристикам судят о пластических свойствах материала?
4. Виды и размеры стандартных образцов, используемых при испытании на растяжение.
5. Вид диаграммы растяжения для образца из малоуглеродистой стали.
6. Что называется пределом пропорциональности, пределом текучести, пределом прочности? Как определяется их величина по диаграмме растяжения?
7. Что такое условный предел текучести?
8. Условные и истинные напряжения.
9. Что такое наклеп?
10. Остаточные и упругие деформации.
11. Как находятся величины относительного остаточного удлинения d и относительного остаточного поперечного сужения y?
12. Как определяются положения осей координат диаграммы растяжения?
Лабораторная работа 3
Рис. 1. Определение прогибов балки
Для определения деформаций воспользуемся уравнением
 (1)
(1)
Из курса математики известна связь кривизны плоской кривой с производными функциями этой кривой:
 (2)
(2)
Приравняв правые части равенств (1) и (2), получим
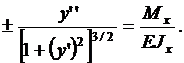 (3)
(3)
Уравнение (3) представляет собой точное дифференциальное уравнение изогнутой оси балки (упругой линии балки). Интегрирование этого нелинейного уравнения представляет большие трудности. Однако для большинства практических задач величиной
 (4)
(4)
ввиду малости деформаций по сравнению с единицей можно пренебречь. Фактическое значение углов поворота сечений балки порядка тысячных долей радиана. Если даже принять  , то и в этом случае величина
, то и в этом случае величина  ничтожно мала по сравнению с единицей.
ничтожно мала по сравнению с единицей.
Отбросив величину  , получим приближенное дифференциальное уравнение упругой линии балки
, получим приближенное дифференциальное уравнение упругой линии балки
 (5)
(5)
интегрирование которого не представляет трудностей.
Выбор знака определяется принятой системой координат.
Для системы координат, показанной на рис. 2, а, момент Мx и кривизна y'' имеют одинаковые знаки и, следовательно, в уравнении (5) следует ставить знак плюс. Для системы координат, представленной на рис.2, б, момент Мx и кривизна y'' имеют противоположные знаки и, следовательно, в уравнении (5) должен быть знак минус.
Перед решением полученного дифференциального уравнения необходимо изгибающий момент Мx представить аналитической функцией от координаты z.

 а) y y
а) y y
 Mx>0 y''<0
Mx>0 y''<0
y''>0 Mx<0

 z z
z z



 б) z z
б) z z




 Mx>0 y''>0
Mx>0 y''>0
y''<0 Mx<0
y y
Рис. 2. Правило знаков при определении прогибов балки
Интегрируя уравнение (5) один раз, получим уравнение углов поворота поперечных сечений
 (6)
(6)
Интегрируя второй раз, получим уравнение прогибов балки
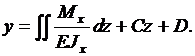 (7)
(7)
Постоянные интегрирования С и D находятся из граничных условий, зависящих от вида опорных связей балки. Для балки (рис. 1) граничные условия имеют вид:
при 
 , при
, при 

 (8)
(8)
Изгибающий момент в сечении z 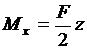 .
.
3. ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА
При исследовании изгиба двухопорной балки используют прибор СМ4А (рис. 3), описание которого дано в лабораторной работе 1.




























 7 5 6 4
7 5 6 4
 А В
А В



 9
9


 3 L 8
3 L 8





 2
2
Рис. 3. Экспериментальная установка СМ4А
Опытное определение величины прогиба в точке D (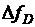 ) производится с помощью индикатора 7. Опытное определение угла поворота сечения в точке В производится с помощью индикатора 8, прикрепленного к неподвижной стойке 4.
) производится с помощью индикатора 7. Опытное определение угла поворота сечения в точке В производится с помощью индикатора 8, прикрепленного к неподвижной стойке 4.
4. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Согласно указанной преподавателем расчетной схеме подготовить установку для выполнения опыта.
2. С помощью штангенциркуля произвести измерения размеров поперечного сечения образца.
3. Нагрузить балку начальной нагрузкой F =20 H.
4. Установить стрелки индикатора 7 на "9,0", а индикатора 8 на нуль.
5. Давая одинаковые приращения  нагрузки, произвести 3 нагружения исследуемого образца в упругой зоне.
нагрузки, произвести 3 нагружения исследуемого образца в упругой зоне.
6. После каждого приращения нагрузки на величину  регистрировать показания индикаторов.
регистрировать показания индикаторов.
7. Определить приращения показаний индикаторов от нагрузки  :
: 
|
|
|



 (1)
(1) - коэффициент пропорциональности.
- коэффициент пропорциональности. а) а в
а) а в F 1 U 31
F 1 U 31 U 32 F 2
U 32 F 2 F 1 U 3(1,2) F 2
F 1 U 3(1,2) F 2 (2)
(2) будут различны, поскольку силы F 1 и F 2 приложены в разных точках.
будут различны, поскольку силы F 1 и F 2 приложены в разных точках. (3)
(3) будет тот же, что и в формуле (1), т.к. сила F 1 прикладывалась первой. Коэффициент
будет тот же, что и в формуле (1), т.к. сила F 1 прикладывалась первой. Коэффициент  , в отличие от
, в отличие от  и тогда
и тогда (4)
(4)























 7 5 6 4
7 5 6 4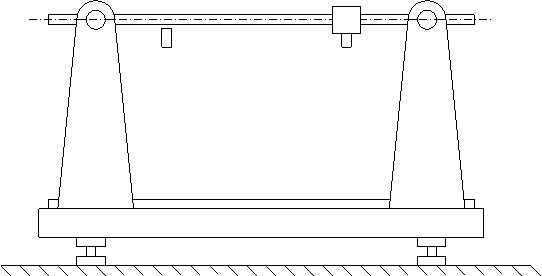
 (5)
(5) (6)
(6)
 , постепенно разгрузить, то диаграмма разгрузки совпадет с начальным участком нагружения ОВ, т.е. в материале развивались только упругие деформации.
, постепенно разгрузить, то диаграмма разгрузки совпадет с начальным участком нагружения ОВ, т.е. в материале развивались только упругие деформации. отрезок (рис. 2)
отрезок (рис. 2) (2)
(2) F
F


 B
B A
A

 O
O

 (3)
(3) (4)
(4) Шейка
Шейка
 (5)
(5) (6)
(6) (7)
(7) (8)
(8)



 l
l




 d0
d0



 l
l






 A0
A0

 l0=11,3
l0=11,3 

 (9)
(9)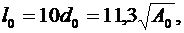 (10)
(10)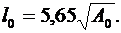 (11)
(11)


 F L
F L

 MF M
MF M

 D
D
 yA
yA


 O Δ l Δ lуп Мl
O Δ l Δ lуп Мl (12)
(12) (13)
(13) (14)
(14)



 (1)
(1) (2)
(2)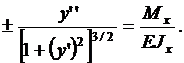 (3)
(3) (4)
(4) , то и в этом случае величина
, то и в этом случае величина  ничтожно мала по сравнению с единицей.
ничтожно мала по сравнению с единицей. (5)
(5)
 а) y y
а) y y



 Mx>0 y''<0
Mx>0 y''<0

 z z
z z


 б) z z
б) z z



 Mx>0 y''>0
Mx>0 y''>0
 (6)
(6)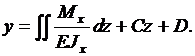 (7)
(7)
 , при
, при 

 (8)
(8)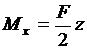 .
.





 А В
А В


 9
9


 3 L 8
3 L 8





 2
2
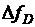 ) производится с помощью индикатора 7. Опытное определение угла поворота сечения в точке В производится с помощью индикатора 8, прикрепленного к неподвижной стойке 4.
) производится с помощью индикатора 7. Опытное определение угла поворота сечения в точке В производится с помощью индикатора 8, прикрепленного к неподвижной стойке 4. нагрузки, произвести 3 нагружения исследуемого образца в упругой зоне.
нагрузки, произвести 3 нагружения исследуемого образца в упругой зоне. регистрировать показания индикаторов.
регистрировать показания индикаторов.


