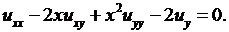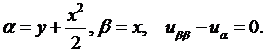Рассмотренные в §2 волновое уравнение, уравнение теплопроводности и уравнение Лапласа существенно отличаются друг от друга. Это отличие заключается и в их физической природе, и в постановке задач, и как увидим ниже, в методах их исследования. Оказывается, что эти уравнения являются представителями трех различных классов, на которые можно разбить большую часть всех уравнений с частными производными второго порядка, линейных относительно вторых производных. Настоящий параграф и будет посвящен этой классификации, при этом мы ограничимся случаем двух независимых переменных.
Итак, рассмотрим уравнение (1.3) в некоторой области  плоскости переменных
плоскости переменных  . Предположим, что коэффициенты уравнения (1.3)
. Предположим, что коэффициенты уравнения (1.3)  имеют производные до второго порядка включительно, непрерывные в области
имеют производные до второго порядка включительно, непрерывные в области  ;
;  - непрерывная функция своих аргументов. Поставим перед собой задачу: с помощью замены независимых переменных
- непрерывная функция своих аргументов. Поставим перед собой задачу: с помощью замены независимых переменных  привести уравнение (1.3) к наиболее простому виду.
привести уравнение (1.3) к наиболее простому виду.
Введем новые переменные:
 (3.1)
(3.1)
От функций (3.1) потребуем, чтобы они были дважды непрерывно дифференцируемыми и чтобы якобиан
 (3.2)
(3.2)
в рассматриваемой области  . Как известно, условие (3.2) является необходимым и достаточным для существования обратного преобразования
. Как известно, условие (3.2) является необходимым и достаточным для существования обратного преобразования
 (3.3)
(3.3)
Преобразования (3.3) позволяют выразить производные в уравнении (1.3) через производные функции  по новым переменным
по новым переменным  . Используя формулы дифференцирования сложных функций нескольких переменных, получаем
. Используя формулы дифференцирования сложных функций нескольких переменных, получаем

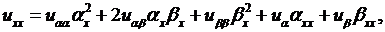
 (3.4)
(3.4)

Подставляя значения производных из (3.4) в (1.3), приходим к уравнению
 (3.5)
(3.5)
где

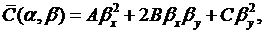 (3.6)
(3.6)

явное выражение  нас не интересует.
нас не интересует.
Функции  найдем так, чтобы обратить некоторые из коэффициентов
найдем так, чтобы обратить некоторые из коэффициентов  в нуль. Из соотношений (3.6) видно, что вопрос об обращении в нуль
в нуль. Из соотношений (3.6) видно, что вопрос об обращении в нуль  и
и  эквивалентен вопросу разрешимости дифференциального уравнения первого порядка вида
эквивалентен вопросу разрешимости дифференциального уравнения первого порядка вида
 (3.7)
(3.7)
относительно неизвестной функции  Поделив уравнение (3.7) на
Поделив уравнение (3.7) на 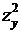 и решая его затем как квадратное уравнение относительно
и решая его затем как квадратное уравнение относительно  , для определения функции
, для определения функции  получим два линейных уравнения с частными производными первого порядка вида
получим два линейных уравнения с частными производными первого порядка вида

 (3.8)
(3.8)
Уравнения (3.8) решаются с помощью системы обыкновенных дифференциальных уравнений, которые в нашем случае имеют вид
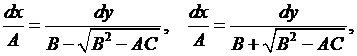
или


Эти уравнения, в свою очередь, могут быть записаны в виде одного уравнения
 (3.9)
(3.9)
 Уравнение (3.9) называется характеристическим уравнением для (1.3). Пусть
Уравнение (3.9) называется характеристическим уравнением для (1.3). Пусть
 (3.10)
(3.10)
- общие решения уравнения (3.9). Кривые (3.10) называются характеристиками уравнения (1.3).
Поведение общих решений (3.10), а следовательно, и искомый простейший вид уравнения (1.3), зависит от знака дискриминанта  Нетрудно проверить, что
Нетрудно проверить, что
 (3.11)
(3.11)
следовательно, знак  не меняется при преобразованиях независимых переменных. В связи с этим классификация уравнений вида (1.3) производится по знаку
не меняется при преобразованиях независимых переменных. В связи с этим классификация уравнений вида (1.3) производится по знаку  .
.
Уравнение (1.3) называется в некоторой точке  области
области  уравнением
уравнением
- гиперболического типа, если 
- эллиптического типа, если 
- параболического типа, если 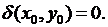
Если в некоторой области  дискриминант
дискриминант  или
или  в
в  , то уравнение (1.3) называется соответственно уравнением гиперболического, эллиптического и параболического типа в области
, то уравнение (1.3) называется соответственно уравнением гиперболического, эллиптического и параболического типа в области  .
.
В приложениях встречаются такие уравнения, у которых  не сохраняет знака во всей рассматриваемой области. Это – так называемые вырождающиеся уравнения и уравнения смешанного типа. Мы ими заниматься не будем.
не сохраняет знака во всей рассматриваемой области. Это – так называемые вырождающиеся уравнения и уравнения смешанного типа. Мы ими заниматься не будем.
Вернемся теперь к задаче упрощения уравнения (1.3), причем каждый тип будем рассматривать в отдельности.
1.  Характеристическое уравнение (3.9) имеет два вещественных и различных общих решения (3.10). За новые переменные
Характеристическое уравнение (3.9) имеет два вещественных и различных общих решения (3.10). За новые переменные  возьмем
возьмем
 (3.12)
(3.12)
Так как функции 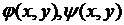 удовлетворяют уравнению (3.7), то из (3.6) получим
удовлетворяют уравнению (3.7), то из (3.6) получим  Из (3.11) следует
Из (3.11) следует  Разделив уравнение (3.5) на
Разделив уравнение (3.5) на  , будем иметь:
, будем иметь:
 (3.13)
(3.13)
где 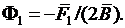
(3.13) есть канонический вид уравнения гиперболического типа.
2.  В этом случае общие решения уравнения (3.9) вещественны и совпадают. Положим
В этом случае общие решения уравнения (3.9) вещественны и совпадают. Положим
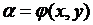 ,
,
а за  возьмем любую дважды непрерывно дифференцируемую функцию, для которой якобиан
возьмем любую дважды непрерывно дифференцируемую функцию, для которой якобиан 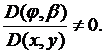 Тогда из (3.6) следует
Тогда из (3.6) следует  Так как
Так как  , то из (3.11) будем иметь
, то из (3.11) будем иметь  Нетрудно показать, что
Нетрудно показать, что  Поделив теперь уравнение (3.5) на
Поделив теперь уравнение (3.5) на  , получим
, получим
 (3.14)
(3.14)
где 
(3.14) есть канонический вид уравнения параболического типа.
3.  В этом случае общие решения (3.10) характеристического уравнения (3.9) являются комплексными величинами. Пусть
В этом случае общие решения (3.10) характеристического уравнения (3.9) являются комплексными величинами. Пусть

- одно из решений (3.10); другое решение будет комплексно сопряженным с указанным. За новые переменные  возьмем
возьмем

Подставляя в уравнение (3.7) его решение  , получаем
, получаем

откуда, разделяя вещественную и мнимую части, будем иметь:


Если учесть соотношения (3.6), то видно, что 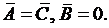 Из (3.11) следует
Из (3.11) следует  Поделив теперь уравнение (3.5) на
Поделив теперь уравнение (3.5) на  , получим
, получим
 (3.15)
(3.15)
(3.15) есть канонический вид уравнения эллиптического типа.
Отметим, что рассмотренные в §2 уравнения колебаний струны (2.8), теплопроводности (2.31), Лапласа (2.38) принадлежат соответственно гиперболическому, параболическому и эллиптическому типу.
Отметим также, что классификация дифференциальных уравнений с частными производными производится и в случае, когда число независимых переменных больше двух [1]. Волновое уравнение (2.17), уравнения теплопроводности (2.29) и Лапласа (2.37) принадлежат соответственно гиперболическому, параболическому и эллиптическому типу.
Пример 3.1. Определить тип уравнения

и привести его к каноническому виду.
Решение. Так как  и
и  , то данное уравнение гиперболического типа. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение
, то данное уравнение гиперболического типа. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение

Решаем его. Получаем

Следовательно, уравнение имеет характеристики 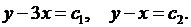 Поэтому в соответствии с (3.12) положим
Поэтому в соответствии с (3.12) положим

Так как 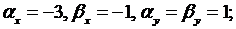 вторые производные функций
вторые производные функций  равны нулю, то с помощью формул (3.4) получаем
равны нулю, то с помощью формул (3.4) получаем
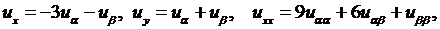

Эти выражения производных подставим в исходное уравнение:


откуда, раскрывая скобки и приводя подобные слагаемые, получаем канонический вид уравнения  .
.
Пример 3.2. Определить тип уравнения

и привести его к каноническому виду.
Решение. Так как  и
и  во всех точках, не лежащих на прямых
во всех точках, не лежащих на прямых  или
или  , то в любом открытом квадранте данное уравнение имеет эллиптический тип. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение
, то в любом открытом квадранте данное уравнение имеет эллиптический тип. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение

Решаем его. Имеем:
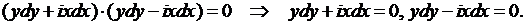
Следовательно, уравнение имеет комплексно сопряженные характеристики  Поэтому полагаем
Поэтому полагаем

Так как 
 то с помощью формул (3.4) находим
то с помощью формул (3.4) находим

Подставив эти значения в исходное уравнение, получим

т.е.  Сокращая на
Сокращая на  приходим к уравнению канонического вида
приходим к уравнению канонического вида 
Пример 3.3. Определить тип уравнения

и привести его к каноническому виду.
Решение. Так как  и
и  , то уравнение параболического типа. Приведем его к каноническому виду. Составим характеристическое уравнение
, то уравнение параболического типа. Приведем его к каноническому виду. Составим характеристическое уравнение

Левая часть этого уравнения есть полный квадрат:  , откуда
, откуда  Это есть уравнение с разделяющимися переменными.
Это есть уравнение с разделяющимися переменными.
Решаем его: 

Итак, характеристическое уравнение имеет одно семейство действительных характеристик. Положим
 ,
,
а за  в соответствии с вышесказанным возьмем любую дважды не-
в соответствии с вышесказанным возьмем любую дважды не-
прерывно дифференцируемую функцию, для которой якобиан  Например, пусть
Например, пусть  Тогда
Тогда
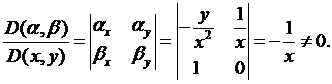
Так как

 то подставляя эти значения производных в (3.4), получаем
то подставляя эти значения производных в (3.4), получаем


Теперь эти выражения производных 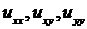 внесем в исходное уравнение. Получим
внесем в исходное уравнение. Получим


откуда  Сократив на
Сократив на  , получим канонический вид заданного уравнения:
, получим канонический вид заданного уравнения: 
Задачи
Определить тип уравнений и привести их к каноническому виду.
3.1. 
Ответ: гиперболический, 
3.2. 
Ответ: параболический, 
3.3. 
Ответ: эллиптический, 
3.4. 
Ответ: гиперболический, 
3.5. 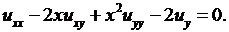
Ответ: параболический, 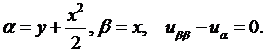
3.6. 
Ответ: гиперболический, 
3.7. 
Ответ: гиперболический, 
3.8. 
Ответ: гиперболический, 
3.9. 
Ответ: эллиптический, 
3.10. 
Ответ: параболический, 



 плоскости переменных
плоскости переменных  . Предположим, что коэффициенты уравнения (1.3)
. Предположим, что коэффициенты уравнения (1.3)  имеют производные до второго порядка включительно, непрерывные в области
имеют производные до второго порядка включительно, непрерывные в области  - непрерывная функция своих аргументов. Поставим перед собой задачу: с помощью замены независимых переменных
- непрерывная функция своих аргументов. Поставим перед собой задачу: с помощью замены независимых переменных  (3.1)
(3.1) (3.2)
(3.2) (3.3)
(3.3) по новым переменным
по новым переменным  . Используя формулы дифференцирования сложных функций нескольких переменных, получаем
. Используя формулы дифференцирования сложных функций нескольких переменных, получаем
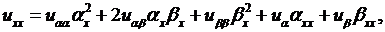
 (3.4)
(3.4)
 (3.5)
(3.5)
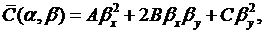 (3.6)
(3.6)
 нас не интересует.
нас не интересует. найдем так, чтобы обратить некоторые из коэффициентов
найдем так, чтобы обратить некоторые из коэффициентов  в нуль. Из соотношений (3.6) видно, что вопрос об обращении в нуль
в нуль. Из соотношений (3.6) видно, что вопрос об обращении в нуль  и
и  эквивалентен вопросу разрешимости дифференциального уравнения первого порядка вида
эквивалентен вопросу разрешимости дифференциального уравнения первого порядка вида (3.7)
(3.7) Поделив уравнение (3.7) на
Поделив уравнение (3.7) на 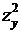 и решая его затем как квадратное уравнение относительно
и решая его затем как квадратное уравнение относительно  , для определения функции
, для определения функции  получим два линейных уравнения с частными производными первого порядка вида
получим два линейных уравнения с частными производными первого порядка вида
 (3.8)
(3.8)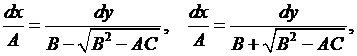


 (3.9)
(3.9) Уравнение (3.9) называется характеристическим уравнением для (1.3). Пусть
Уравнение (3.9) называется характеристическим уравнением для (1.3). Пусть (3.10)
(3.10) Нетрудно проверить, что
Нетрудно проверить, что (3.11)
(3.11) не меняется при преобразованиях независимых переменных. В связи с этим классификация уравнений вида (1.3) производится по знаку
не меняется при преобразованиях независимых переменных. В связи с этим классификация уравнений вида (1.3) производится по знаку  области
области 

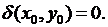
 дискриминант
дискриминант  или
или  в
в  , то уравнение (1.3) называется соответственно уравнением гиперболического, эллиптического и параболического типа в области
, то уравнение (1.3) называется соответственно уравнением гиперболического, эллиптического и параболического типа в области  не сохраняет знака во всей рассматриваемой области. Это – так называемые вырождающиеся уравнения и уравнения смешанного типа. Мы ими заниматься не будем.
не сохраняет знака во всей рассматриваемой области. Это – так называемые вырождающиеся уравнения и уравнения смешанного типа. Мы ими заниматься не будем. Характеристическое уравнение (3.9) имеет два вещественных и различных общих решения (3.10). За новые переменные
Характеристическое уравнение (3.9) имеет два вещественных и различных общих решения (3.10). За новые переменные  (3.12)
(3.12)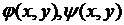 удовлетворяют уравнению (3.7), то из (3.6) получим
удовлетворяют уравнению (3.7), то из (3.6) получим  Из (3.11) следует
Из (3.11) следует  Разделив уравнение (3.5) на
Разделив уравнение (3.5) на  , будем иметь:
, будем иметь: (3.13)
(3.13)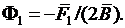
 В этом случае общие решения уравнения (3.9) вещественны и совпадают. Положим
В этом случае общие решения уравнения (3.9) вещественны и совпадают. Положим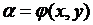 ,
, возьмем любую дважды непрерывно дифференцируемую функцию, для которой якобиан
возьмем любую дважды непрерывно дифференцируемую функцию, для которой якобиан 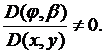 Тогда из (3.6) следует
Тогда из (3.6) следует  Так как
Так как  , то из (3.11) будем иметь
, то из (3.11) будем иметь  Нетрудно показать, что
Нетрудно показать, что  Поделив теперь уравнение (3.5) на
Поделив теперь уравнение (3.5) на  (3.14)
(3.14)
 В этом случае общие решения (3.10) характеристического уравнения (3.9) являются комплексными величинами. Пусть
В этом случае общие решения (3.10) характеристического уравнения (3.9) являются комплексными величинами. Пусть

 , получаем
, получаем


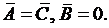 Из (3.11) следует
Из (3.11) следует  Поделив теперь уравнение (3.5) на
Поделив теперь уравнение (3.5) на  (3.15)
(3.15)
 и
и  , то данное уравнение гиперболического типа. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение
, то данное уравнение гиперболического типа. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение

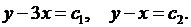 Поэтому в соответствии с (3.12) положим
Поэтому в соответствии с (3.12) положим
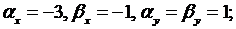 вторые производные функций
вторые производные функций 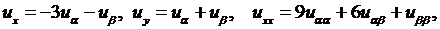



 .
.
 и
и  во всех точках, не лежащих на прямых
во всех точках, не лежащих на прямых  или
или  , то в любом открытом квадранте данное уравнение имеет эллиптический тип. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение
, то в любом открытом квадранте данное уравнение имеет эллиптический тип. Приведем его к каноническому виду. В соответствии с (3.9) составим характеристическое уравнение
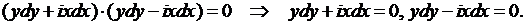
 Поэтому полагаем
Поэтому полагаем

 то с помощью формул (3.4) находим
то с помощью формул (3.4) находим

 Сокращая на
Сокращая на  приходим к уравнению канонического вида
приходим к уравнению канонического вида 

 и
и  , то уравнение параболического типа. Приведем его к каноническому виду. Составим характеристическое уравнение
, то уравнение параболического типа. Приведем его к каноническому виду. Составим характеристическое уравнение
 , откуда
, откуда  Это есть уравнение с разделяющимися переменными.
Это есть уравнение с разделяющимися переменными.

 ,
, Например, пусть
Например, пусть  Тогда
Тогда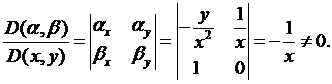

 то подставляя эти значения производных в (3.4), получаем
то подставляя эти значения производных в (3.4), получаем

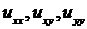 внесем в исходное уравнение. Получим
внесем в исходное уравнение. Получим

 Сократив на
Сократив на  , получим канонический вид заданного уравнения:
, получим канонический вид заданного уравнения: