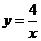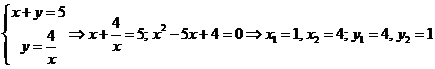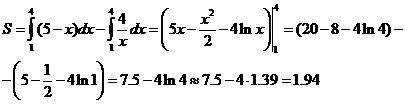В декартовой системе координат за основную фигуру, площадь которой выражается определенным интегралом, принимается криволинейная трапеция. Если y=f(x) – уравнение линии, ограничивающей трапецию, то площадь трапеции S (в предположении, что y³0) равна S= 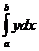 , где пределы интегрирования a и b(a<b) - абсциссы начала и конца линии.
, где пределы интегрирования a и b(a<b) - абсциссы начала и конца линии.
Если линия задана параметрическими уравнениями x=j(t), y=y(t), то совершая подстановку в интеграле по формуле x=j(t), получим
S= 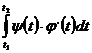 ,
,
где t1 и t2- значения, между которыми изменяется параметр t, когда точка пробегает слева направо всю линию, ограничивающую трапецию сверху.

 Пусть дано тело, ограниченное замкнутой поверхностью, пусть известна площадь любого его сечения, проведенного плоскостью, перпендикулярной к некоторой прямой, например к оси абсцисс:
Пусть дано тело, ограниченное замкнутой поверхностью, пусть известна площадь любого его сечения, проведенного плоскостью, перпендикулярной к некоторой прямой, например к оси абсцисс:
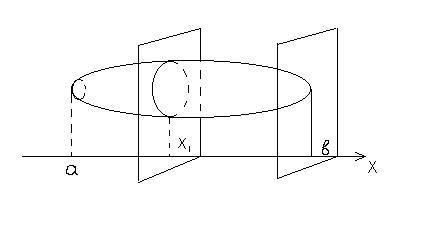
При этом можно считать, что площадь такого сечения является известной нам функцией S(x), где x – абсцисса точки пересечения указанной плоскости с осью х. Далее предполагается, что все тело заключено между двумя перпендикулярными к оси х плоскостями, пересекающими ее в точках a и b (a<b). Для определения объема такого тела разобьем его на слои с помощью секущих плоскостей, перпендикулярных к оси х и пересекающих ее в точках x0=a, x2,…, xn=b. Каждый слой заменим цилиндром с той же высотой и основанием, равным S(x). Объем прямого цилиндра равен произведению площади его основания на высоту. Объем вычисляют как предел при n®¥ суммы объемов, образующих ступенчатое тело и получаем
V= 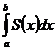
Если тело получено вращением криволинейной трапеции, ограниченной линией y=f(x), вокруг оси Ох, то поперечным сечением с абсциссой х служит круг, радиус которого равен соответствующей ординате линии y=f(x)
S(x)=py2 Þ Vx= 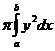 , где y=f(x).
, где y=f(x).
Получена формула объема тела, полученного вращением линии y=f(x) вокруг оси Ох. Аналогично получается формула объема тела, полученного вращением трапеции вокруг оси Оу. Там возможны две формулы:
Vy= 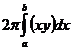 или Vy=
или Vy= 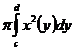 , где c и d на оси Оу.
, где c и d на оси Оу.
Длина дуги AB кривой y=f(x) есть предел длины вписанной в нее ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих сторон к нулю:
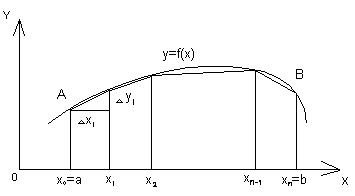
Линия AB задана уравнением y=f(x). Длина дуги AB вычисляется по формуле
L= 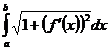 или L=
или L= 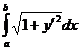 .
.
Если dx внести под знак корня, то формулу можно переписать в виде
L= 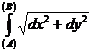 .
.
Если уравнение линии задано параметрически: x=x(t), y=y(t) и t1,t2 – значение параметра t, соответствующие концам дуги, причем t1<t2, то
L= 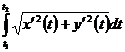

Задания на контрольную работу № 3
№№ 1.1-1.30. Найдите интегралы.
1.1 a) 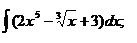
| 1.11 a) 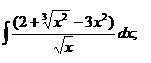
| 1.21 a) 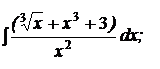
|
b) 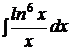 ; ;
| b) 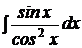 ; ;
| b) 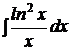 ; ;
|
c) 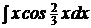 ; ;
| c) 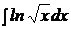 ; ;
| c) 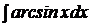 ; ;
|
d) 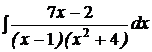 ; ;
| d) 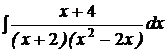 ; ;
| d) 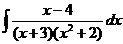 ; ;
|
e) 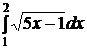 ; ;
| e) 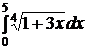 ; ;
| e) 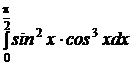 ; ;
|
1.2. a) 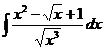 ; ;
| 1.12 a) 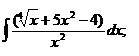
| 1.22a) 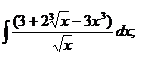
|
b) 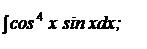
| b) 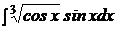 ; ;
| b) 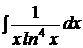 ; ;
|
c) 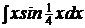 ; ;
| c) 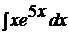 ; ;
| c) 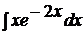 ; ;
|
d) 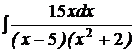 ; ;
| d) 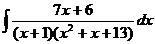 ; ;
| d) 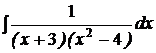 ; ;
|
e) 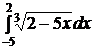 ; ;
| e) 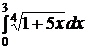 ; ;
| e) 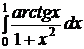 ; ;
|
1.3.a) 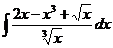 ; ;
| 1.13 a) 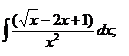
| 1.23 a) 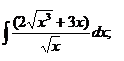
|
b) 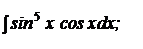
| b) 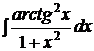 ; ;
| b) 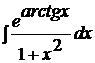 ; ;
|
c) 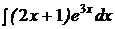 ; ;
| c) 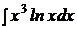 ; ;
| c) 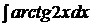 ; ;
|
d) 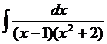 ; ;
| d) 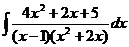 ; ;
| d) 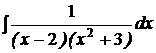 ; ;
|
e) 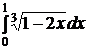 ; ;
| e) 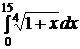 ; ;
| e) 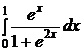 ; ;
|
1.4. a) 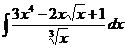 ; ;
| 1.14 a) 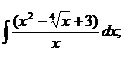
| 1.24 a) 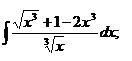
|
b) 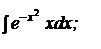
| b) 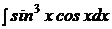 ; ;
| b) 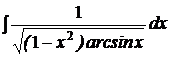 ; ;
|
c) 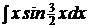 ; ;
| c) 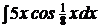 ; ;
| c)  ; ;
|
d) 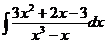 ; ;
| d) 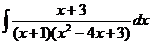 ; ;
| d) 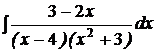 ; ;
|
e) 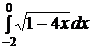 ; ;
| e) 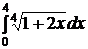 ; ;
| e) 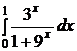 ; ;
|
1.5. a) 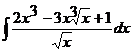 ; ;
| 1.15 a) 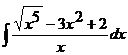 ; ;
| 1.25 a) 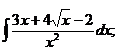
|
b) 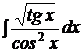 ; ;
| b) 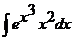 ; ;
| b) 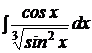 ; ;
|
c) 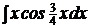 ; ;
| c) 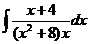 ; ;
| c) 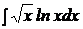 ; ;
|
d) 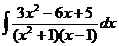 ; ;
| d)  ; ;
| d) 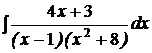 ; ;
|
e) 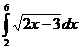 ; ;
| e) 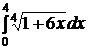 ; ;
| e) 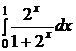 ; ;
|
1.6.a) 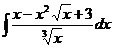 ; ;
| 1.16 a) 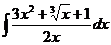 ; ;
| 1.26 a) 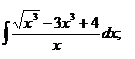
|
b) 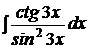 ; ;
| b)  ; ;
| b) 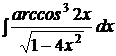 ; ;
|
c) 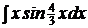 ; ;
| c) 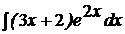 ; ;
| c) 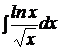 ; ;
|
d) 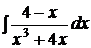 ; ;
| d) 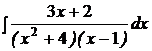 ; ;
| d) 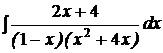 ; ;
|
e) 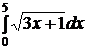 ; ;
| e) 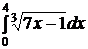 ; ;
| e) 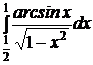 ; ;
|
1.7.a) 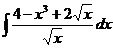 ; ;
| 1.17 a) 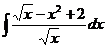 ; ;
| 1.27 a) 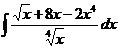 ; ;
|
b) 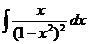 ; ;
| b) 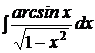 ; ;
| b) 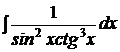 ; ;
|
c) 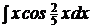 ; ;
| c) 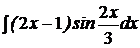 ; ;
| c) 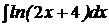 ; ;
|
d) 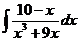 ; ;
| d) 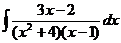 ; ;
| d) 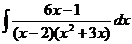 ; ;
|
e) 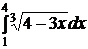 ; ;
| e) 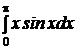 ; ;
| e) 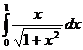 ; ;
|
1.8. a) 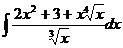 ; ;
| 1.18 a) 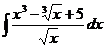 ; ;
| 1.28 a) 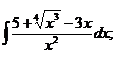
|
b) 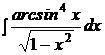 ; ;
| b) 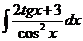 ; ;
| b) 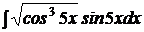 ; ;
|
c) 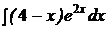 ; ;
| c) 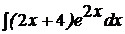 ; ;
| c) 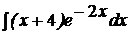 ; ;
|
d) 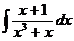 ; ;
| d) 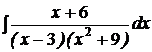 ; ;
| d) 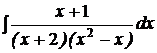 ; ;
|
e) 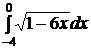 ; ;
| e) 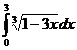 ; ;
| e) 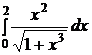 ; ;
|
1.9. a) 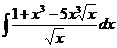 ; ;
| 1.19 a) 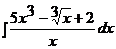 ; ;
| 1.29 a) 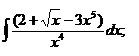
|
b) 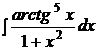 ; ;
| b) 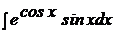 ; ;
| b) 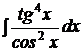 ; ;
|
c) 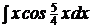 ; ;
| c)  ; ;
| c) 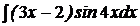 ; ;
|
d) 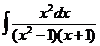 ; ;
| d) 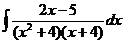 ; ;
| d) 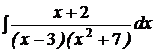 ; ;
|
e) 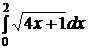 ; ;
| e) 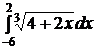 ; ;
| e) 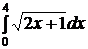 ; ;
|
1.10. a) 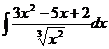 ; ;
| 1.20 a) 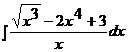 ; ;
| 1.30a) 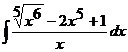 ; ;
|
b) 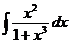 ; ;
| b) 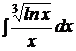 ; ;
| b) 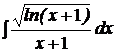 ; ;
|
c) 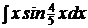 ; ;
| c) 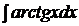 ; ;
| c) 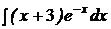 ; ;
|
d) 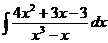 ; ;
| d) 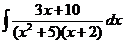 ; ;
| d) 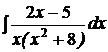 ; ;
|
e) 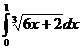 ; ;
| e) 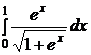 ; ;
| e) 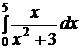 ; ;
|
№№ 2.1-2.30. Вычислите определенные интегралы по формуле Ньютона – Лейбница.
2.1. 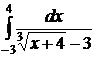 ; ;
| 2.2. 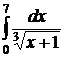 ; ;
| 2.3. 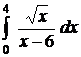 ; ;
| 2.4. 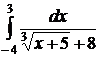 ; ;
| 2.5. 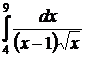 ; ;
| 2.6. 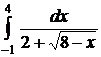 ; ;
| 2.7. 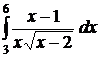 ; ;
| 2.8 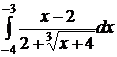 ; ;
| 2.9. 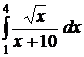 ; ;
| 2.10. 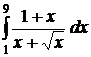 ; ;
| 2.11. 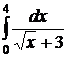 ; ;
| 2.12. 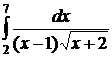 ; ;
| 2.13. 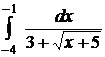 ; ;
| 2.14. 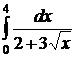 ; ;
| 2.15. 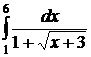 ; ;
| 2.16. 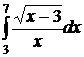
| 2.17 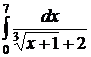 ; ;
| 2.18. 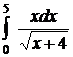 ; ;
| 2.19. 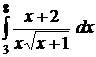 ; ;
| 2.20. 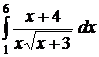 ; ;
| 2.21. 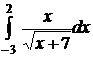 ; ;
| 2.22. 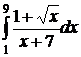 ; ;
| 2.23. 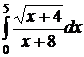 ; ;
| 2.24. 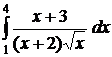 ; ;
| 2.25. 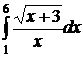 ; ;
| 2.26. 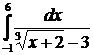 ; ;
| 2.27. 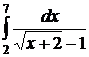 ; ;
| 2.28. 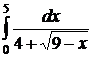
| 2.29. 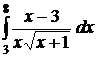 ; ;
| 2.30. 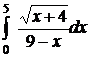 . .
|
№№ 3.1-3.30. Вычислите несобственные интегралы или докажите их расходимость.
3.1. 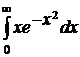
| 3.2. 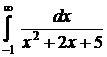
| 3.3. 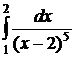
| 3.4. 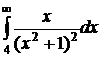
| 3.5. 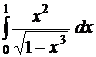
| 3.6. 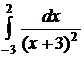
| 3.7. 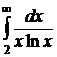
| 3.8. 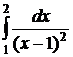
| 3.9. 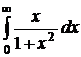
| 3.10. 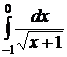
| 3.11 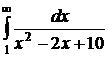
| 3.12. 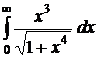
| 3.13. 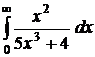
| 3.14. 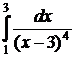
| 3.15. 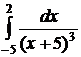
| 3.16. 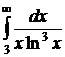 . .
| 3.17. 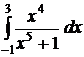
| 3.18. 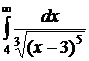
| 3.19. 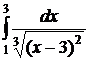
| 3.20. 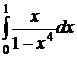 . .
| 3.21. 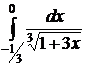
| 3.22. 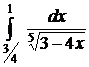
| 3.23. 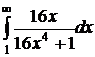
| 3.24. 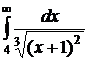 . .
| 3.25. 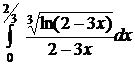
| 3.26. 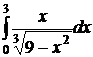
| 3.27. 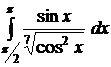
| 3.28. 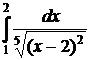 . .
| 3.29. 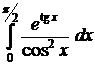 . .
| 3.30 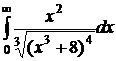
|
№№ 4.1-4.30. Произвести вычисления.
4.1. Вычислите площадь фигуры, ограниченной параболой 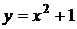 и прямой и прямой 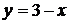 . .
4.2. Вычислите длину дуги кривой 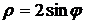 . .
4.3. Вычислите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми 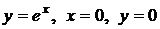 ,x=1. ,x=1.
4.4. Вычислите площадь фигуры, ограниченной линией 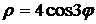 . .
4.5. Вычислите длину дуги арки циклоиды 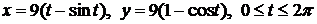 . .
4.6. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболой 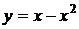 и прямой и прямой 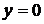 . .
4.7. Вычислите длину дуги кривой 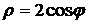 . .
4.8. Вычислите площадь фигуры, ограниченной линиями 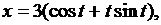 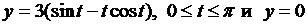 . .
4.9. Вычислите длину дуги полукубической параболы 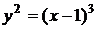 от точки от точки 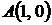 до точки до точки 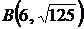 . .
4.10. Вычислите площадь фигуры, ограниченной линией 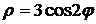 . .
4.11. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линией  . .
4.12. Вычислите длину дуги полукубической параболы 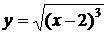 от точки от точки 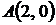 до точки до точки 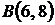 . .
4.13. Вычислите площадь фигуры, ограниченной кардиоидой 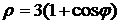 . .
4.14. Вычислите площадь фигуры, ограниченной линиями 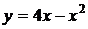 и и 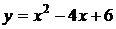 . .
4.15. Вычислите площадь фигуры, ограниченной одной аркой циклоиды 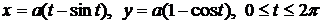 и осью Ох. и осью Ох.
4.16. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривыми 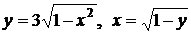 и осью Оу и осью Оу 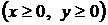 . .
4.17. Вычислите длину дуги кардиоиды 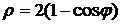 . .
4.18. Вычислите объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболами 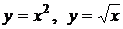 . .
4.19. Вычислите площадь фигуры, ограниченной параболой 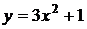 и прямой и прямой 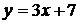 . .
4.20. Вычислите длину астроиды 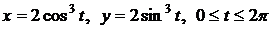 . .
4.21. Вычислите площадь фигуры, ограниченной четырехлепестковой розой 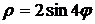 . .
4.22. Вычислите длину дуги кривой 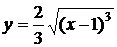 , ограниченной прямыми , ограниченной прямыми 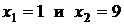 . .
4.23. Вычислите площадь фигуры, ограниченной линиями 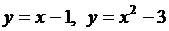 . .
4.24. Вычислите объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной кривыми 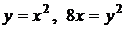 . .
4.25. Вычислите площадь фигуры, ограниченной линией 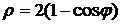 . .
4.26. Вычислите длину дуги кривой 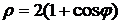 . .
4.27. Вычислите длину дуги данной линии 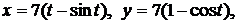 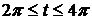 . .
4.28. Вычислите объем тела, полученного вращением вокруг оси Оу линии 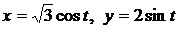 . .
4.29. Вычислите площадь фигуры, ограниченной астроидой 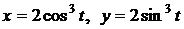 . .
4.30. Вычислите площадь фигуры, ограниченной линиями 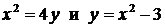 . .
|
|
|
Пример решения заданий контрольной работы № 3
Задание №1.
a) Вычислить интеграл: 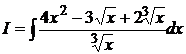
Решение:
Преобразуем подынтегральное выражение
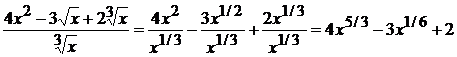 . Следовательно,
. Следовательно,
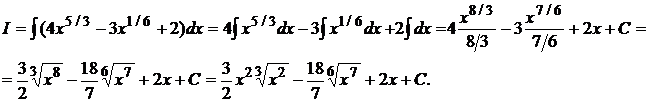
Здесь мы воспользовались свойствами неопределенного интеграла и формулами 2 и 1 таблицы интегралов. Сделаем проверку правильности интегрирования. Найдем 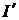 .
.
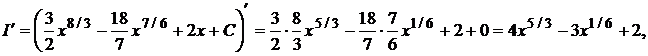
что совпадает с преобразованным подынтегральным выражением.
b) Вычислить интеграл: 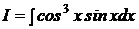
Решение:
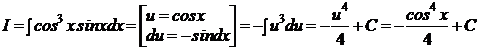
Проверка: 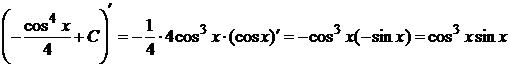 ,
,
что совпадает с подынтегральным выражением.
c) Вычислить: 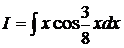 .
.
Решение:
Все необходимые вычисления будем проводить одновременно с применением формулы 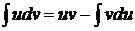
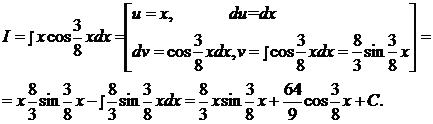
d) Вычислить интеграл: 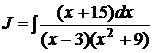 .
.
Решение:
Разложим подынтегральную дробь на простейшие дроби:
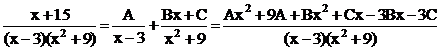 .
.
Следовательно х + 15 º (А + В) х 2 + (С – 3 В) х + 9 А – 3 С.
Сравним коэффициенты при одинаковых степенях х в левой и правой частях:
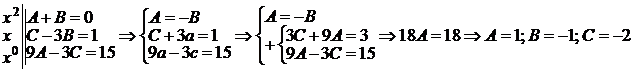
Итак:
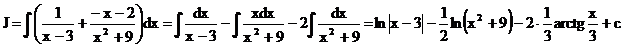 .e) Вычислите интеграл
.e) Вычислите интеграл 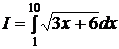
Решение:
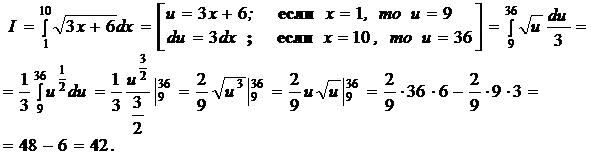
Задание 2. Вычислить определенный интеграл
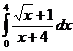
Решение. 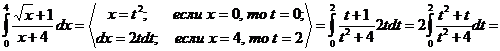
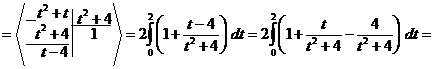
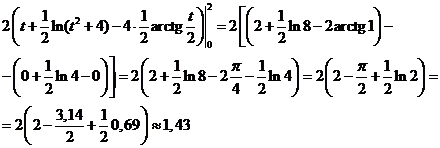
При вычислении этого интеграла были применены формулы
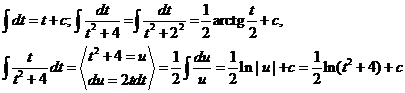
Задание 3 Вычислить несобственный интеграл 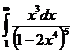 или доказать его расходимость
или доказать его расходимость
Решение.
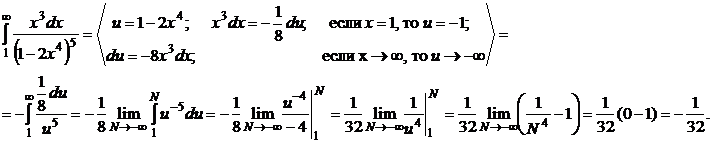
Таким образом, несобственный интеграл равен 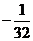 , т. е. он сходится.
, т. е. он сходится.
Задание 4 Найти площадь фигуры, ограниченной линиями 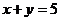 ,
, 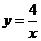
Решение. Первое уравнение определяет на плоскости прямую линию, второе – гиперболу (рис. 2).
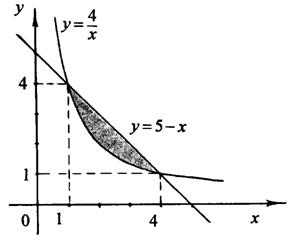
рис. 2
Найдем их точки пересечения
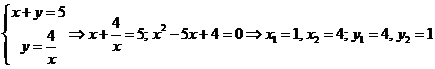
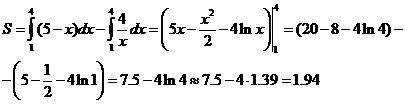



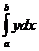 , где пределы интегрирования a и b(a<b) - абсциссы начала и конца линии.
, где пределы интегрирования a и b(a<b) - абсциссы начала и конца линии.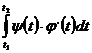 ,
,

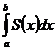
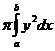 , где y=f(x).
, где y=f(x).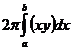 или Vy=
или Vy= 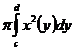 , где c и d на оси Оу.
, где c и d на оси Оу.
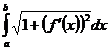 или L=
или L= 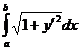 .
.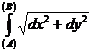 .
.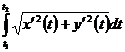

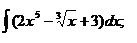
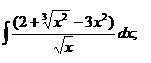
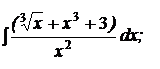
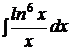 ;
;
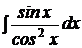 ;
;
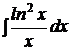 ;
;
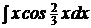 ;
;
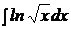 ;
;
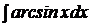 ;
;
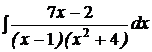 ;
;
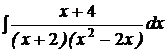 ;
;
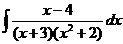 ;
;
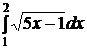 ;
;
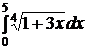 ;
;
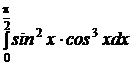 ;
;
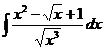 ;
;
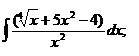
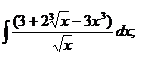
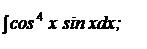
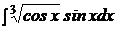 ;
;
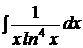 ;
;
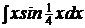 ;
;
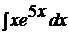 ;
;
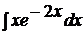 ;
;
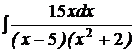 ;
;
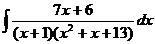 ;
;
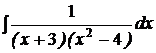 ;
;
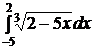 ;
;
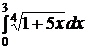 ;
;
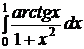 ;
;
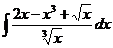 ;
;
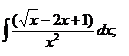
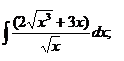
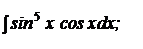
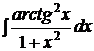 ;
;
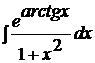 ;
;
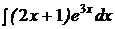 ;
;
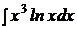 ;
;
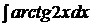 ;
;
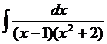 ;
;
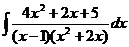 ;
;
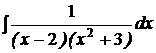 ;
;
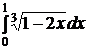 ;
;
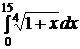 ;
;
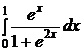 ;
;
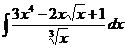 ;
;
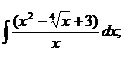
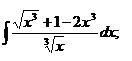
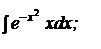
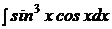 ;
;
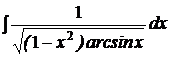 ;
;
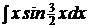 ;
;
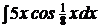 ;
;
 ;
;
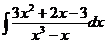 ;
;
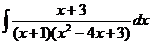 ;
;
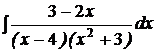 ;
;
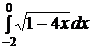 ;
;
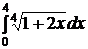 ;
;
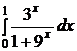 ;
;
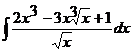 ;
;
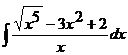 ;
;
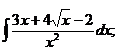
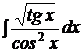 ;
;
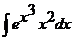 ;
;
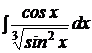 ;
;
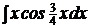 ;
;
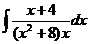 ;
;
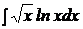 ;
;
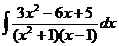 ;
;
 ;
;
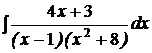 ;
;
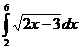 ;
;
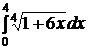 ;
;
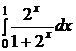 ;
;
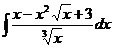 ;
;
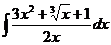 ;
;
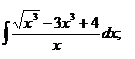
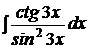 ;
;
 ;
;
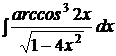 ;
;
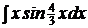 ;
;
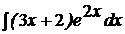 ;
;
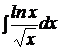 ;
;
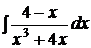 ;
;
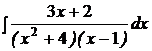 ;
;
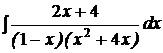 ;
;
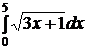 ;
;
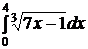 ;
;
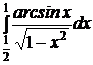 ;
;
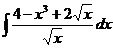 ;
;
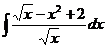 ;
;
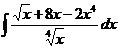 ;
;
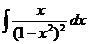 ;
;
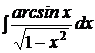 ;
;
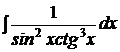 ;
;
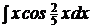 ;
;
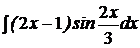 ;
;
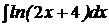 ;
;
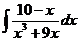 ;
;
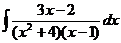 ;
;
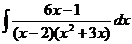 ;
;
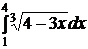 ;
;
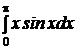 ;
;
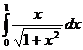 ;
;
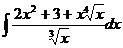 ;
;
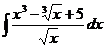 ;
;
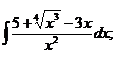
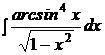 ;
;
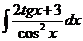 ;
;
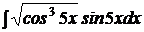 ;
;
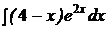 ;
;
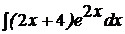 ;
;
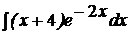 ;
;
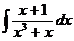 ;
;
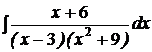 ;
;
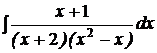 ;
;
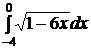 ;
;
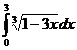 ;
;
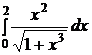 ;
;
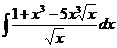 ;
;
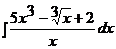 ;
;
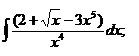
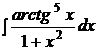 ;
;
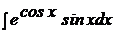 ;
;
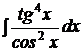 ;
;
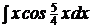 ;
;
 ;
;
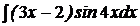 ;
;
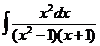 ;
;
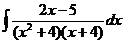 ;
;
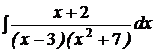 ;
;
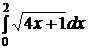 ;
;
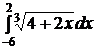 ;
;
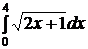 ;
;
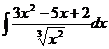 ;
;
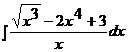 ;
;
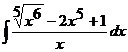 ;
;
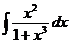 ;
;
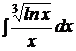 ;
;
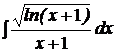 ;
;
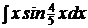 ;
;
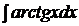 ;
;
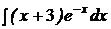 ;
;
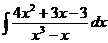 ;
;
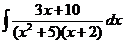 ;
;
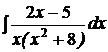 ;
;
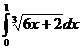 ;
;
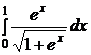 ;
;
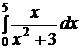 ;
;
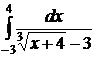 ;
;
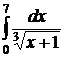 ;
;
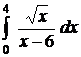 ;
;
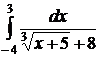 ;
;
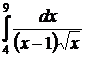 ;
;
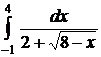 ;
;
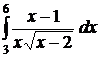 ;
;
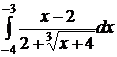 ;
;
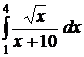 ;
;
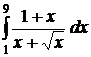 ;
;
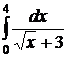 ;
;
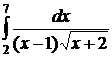 ;
;
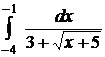 ;
;
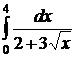 ;
;
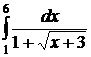 ;
;
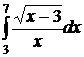
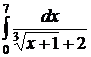 ;
;
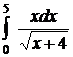 ;
;
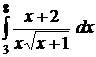 ;
;
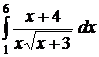 ;
;
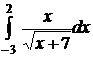 ;
;
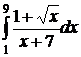 ;
;
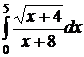 ;
;
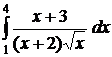 ;
;
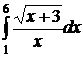 ;
;
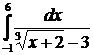 ;
;
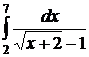 ;
;
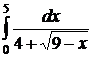
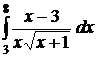 ;
;
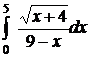 .
.
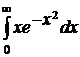
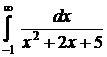
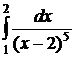
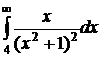
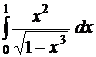
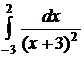
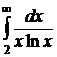
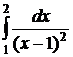
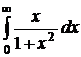
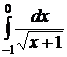
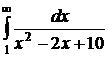
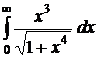
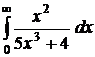
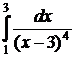
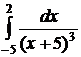
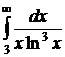 .
.
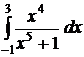
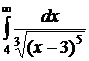
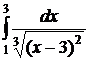
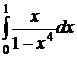 .
.
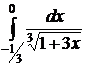
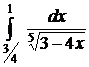
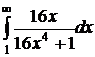
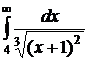 .
.
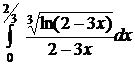
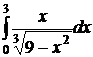
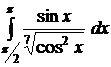
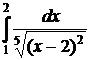 .
.
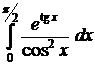 .
.
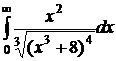
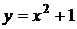 и прямой
и прямой 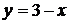 .
.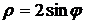 .
.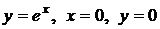 ,x=1.
,x=1.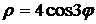 .
.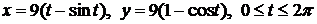 .
.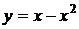 и прямой
и прямой 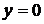 .
.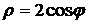 .
.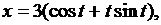
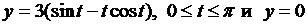 .
.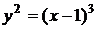 от точки
от точки 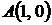 до точки
до точки 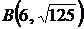 .
.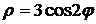 .
. .
.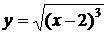 от точки
от точки 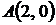 до точки
до точки 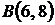 .
.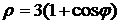 .
.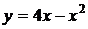 и
и 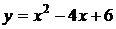 .
.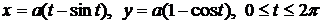 и осью Ох.
и осью Ох.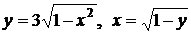 и осью Оу
и осью Оу 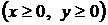 .
.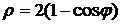 .
.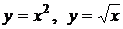 .
.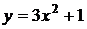 и прямой
и прямой 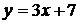 .
.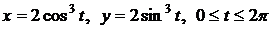 .
.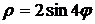 .
.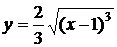 , ограниченной прямыми
, ограниченной прямыми 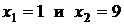 .
.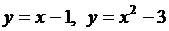 .
.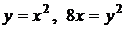 .
.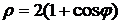 .
.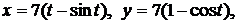
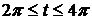 .
.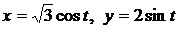 .
.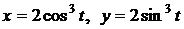 .
.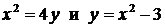 .
.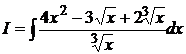
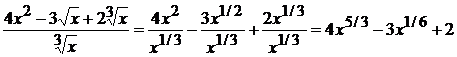 . Следовательно,
. Следовательно,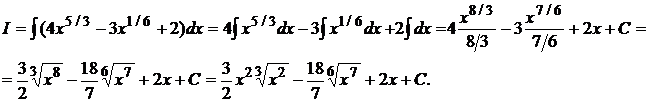
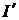 .
.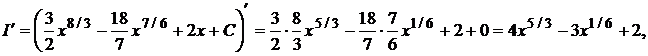
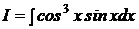
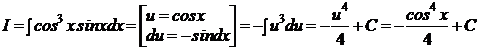
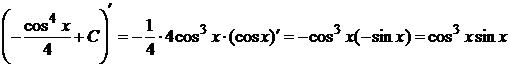 ,
,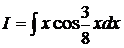 .
.
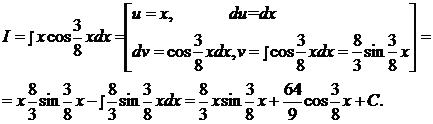
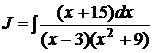 .
.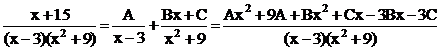 .
.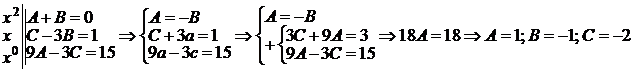
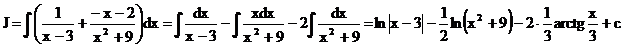 .e) Вычислите интеграл
.e) Вычислите интеграл 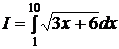
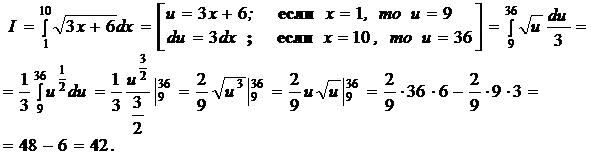
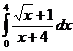
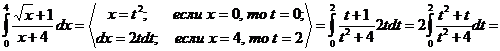
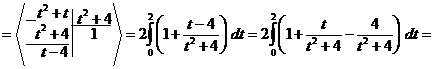
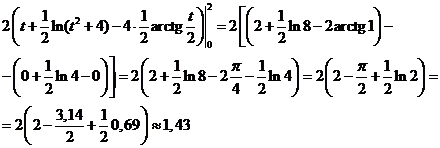
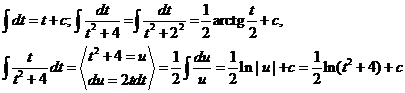
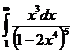 или доказать его расходимость
или доказать его расходимость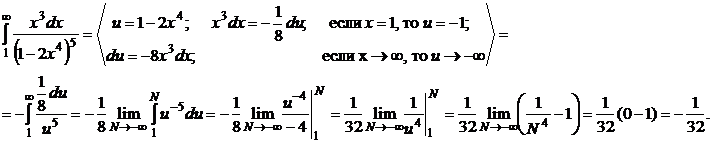
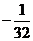 , т. е. он сходится.
, т. е. он сходится.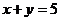 ,
,