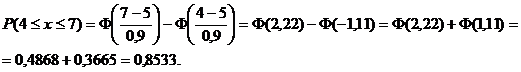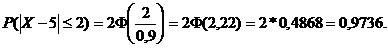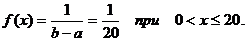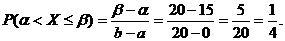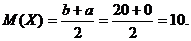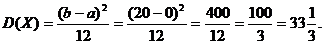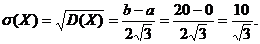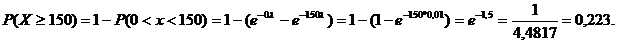Испытания называются независимыми по отношению к некоторому событиюА, если вероятность наступления данного события в каждом испытании постоянная и не зависит от результатов других испытаний.
Введем обозначения: Р(А) = р, P( 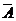 ) = 1-p = q.
) = 1-p = q.
Рассмотрим событие, состоящее в том, что событие А наступит в n независимых испытаниях m раз. Для определения вероятности данного события применяется формула Бернулли: 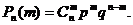
При большом количестве испытаний для расчетов следует применять вместо формулы Бернулли асимптотические формулы.
Для вычисления вероятности m -кратного наступления редкого события служит формула Пуассона: 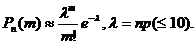
Для вычисления вероятности m-кратного наступления нередкого события служит асимптотическая формула Муавра – Лапласа:
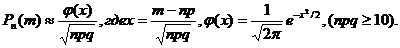
Для вычисления вероятности того, что число наступлений события заключено в заданных границах, служит асимптотическая интегральная формула Муавра – Лапласа:
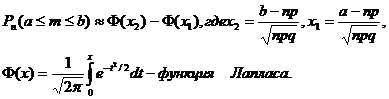
Следствия из интегральной формулы Муавра – Лапласа:
1. 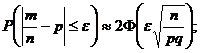
2. 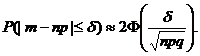
Пример 3.1. В среднем 20% продукции предприятия изготавливается на экспорт. Найти вероятность того, что из пяти наудачу избранных изделий предприятия на экспорт пойдет: а) три изделия: б) менее двух.
Решение. СобытиеАсостоит в том, что наудачу выбранное изделие пойдет на экспорт. Для всех изделий вероятность данного события одинакова. Р(А)=0,2=р; P(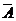 )=0,8 = q. Имеют место независимыеповторные испытания, число которых невелико n=5. Для определения вероятности того, что событие А в серии из n независимых испытаний наступит ровно m раз следует применить формулу Бернулли.
)=0,8 = q. Имеют место независимыеповторные испытания, число которых невелико n=5. Для определения вероятности того, что событие А в серии из n независимых испытаний наступит ровно m раз следует применить формулу Бернулли.
a) три изделия из выбранных пяти пойдут на экспорт:
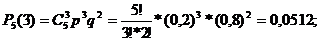
b) менее двух изделий означает либо одно, либо ни одного:
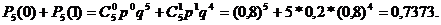
Пример 3.2. Вероятность ошибки при передаче знака текстовой информации равна 0,002. Найти вероятность того, что при передаче 1000 знаков будет: а) четыре ошибки; б) не более двух ошибок.
Решение. СобытиеАсостоит в том, что при передаче знака будет допущена ошибка. Для всех знаков вероятность данного события одинакова и очень мала. Р(А) =0,002 = р; P(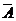 )= 0,998 =q. Имеют место независимыеповторные испытания, число которых велико: n =1000, np =l=2. Найдем вероятность того, что «редкое событие» А наступит в серии из n независимых испытаний m раз. Для определения вероятности «редкого события» следует применять формулу Пуассона:
)= 0,998 =q. Имеют место независимыеповторные испытания, число которых велико: n =1000, np =l=2. Найдем вероятность того, что «редкое событие» А наступит в серии из n независимых испытаний m раз. Для определения вероятности «редкого события» следует применять формулу Пуассона:
a) при передаче 1000 знаков будет 4 ошибки:
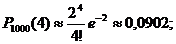
b) не более двух ошибок – это две, одна или ни одной:
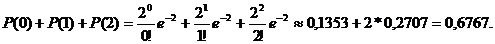
Пример 3.3. В среднем 90% выпускников Вуза устраиваются в течение года на работу по полученной специальности. Найти вероятность того, что из 900 выпускников университета этого года в течение года устроится на работу по полученной специальности: а) 795; b) не менее 795.
Решение. СобытиеАсостоит в том, что наудачу выбранный студент устроится на работу в течение года по специальности. Для всех выпускников вероятность данного события одинакова. Р(А) = 0,9 = р; Р(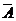 )= 0,1 = q. Имеют место независимые повторные испытания, число которых велико n=900. Для определения вероятности того, что событие А наступит в n независимых испытаниях m раз следует применять асимптотические формулы.
)= 0,1 = q. Имеют место независимые повторные испытания, число которых велико n=900. Для определения вероятности того, что событие А наступит в n независимых испытаниях m раз следует применять асимптотические формулы.
a) Для определения вероятности того, что устроится на работу по специальности в течение года 795 выпускников университета следует использовать формулу Муавра-Лапласа. По условиям задачи:
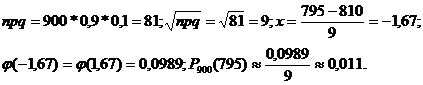
b) Для определения вероятности того, что устроится на работу по специальности в течение года не менее 795 из 900 выпускников, следует использовать интегральную формулу Муавра-Лапласа. По условиям задачи:
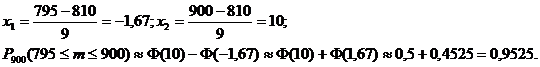
Пример 3.4. Какое количество бросков игральной кости следует сделать, чтобы частота выпадения шести очков отличалась от вероятности этого события не более чем на 0,01 с вероятностью не менее 0,9545.
Решение. СобытиеАсостоит в том, что при броске игральной кости выпадет шесть очков. Для всех бросков вероятность данного события одинакова. Р(А) = 1/6 = р; Р( 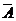 ) = 5/6=q. Имеют место независимые повторныеиспытания, число которых велико. Для определения необходимого количества бросков можно использовать следствие из интегральной формулы Муавра – Лапласа. По условиям задачи:
) = 5/6=q. Имеют место независимые повторныеиспытания, число которых велико. Для определения необходимого количества бросков можно использовать следствие из интегральной формулы Муавра – Лапласа. По условиям задачи:
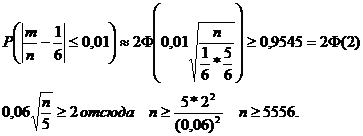
Пример 3.5. Отдел контроля проверяет качество 1000 изделий. Известно, что в среднем 10% данной продукции имеют какие-либо дефекты. Найти с вероятностью 0,9973 границы, в которых будет заключено количество изделий с дефектами.
Решение. СобытиеАсостоит в том, что наудачу выбранное изделие имеет дефекты. Для всех изделий вероятность данного события одинакова. р=0,1; q= 0,9. Имеют место независимые повторные испытания, число которых велико. Для определения границ, в которых будет заключено количество изделий с дефектами, можно использовать следствие из интегральной формулы Муавра – Лапласа. По условиям задачи:
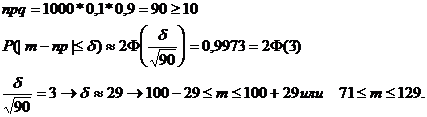
5. Дискретная случайная величина (ДСВ) Способ задания ДСВ.ДСВ с биноминальным законом распределения. Функция распределения ДСВ.Числовые характеристики ДСВ как они определяются и что характеризируют.Вероятность попадания ДСВ в интервал.
Случайная величина Х - это переменная, которая может принимать в зависимости от исходов испытаний те или иные случайные значения хi. Если все значения случайных величин составляют счетное множество, то случайная величина называется дискретной. Ряд количественных показателей экономических систем могут быть рассмотрены как дискретные случайные величины.
Закон распределения случайной дискретной величины связывает между собой значения случайной величины и вероятности принятия случайной величиной ее значений. Он может быть записан в форме таблицы:
| Xi
| X0
| X1
| X2
| …
| Xk
| ИТОГО
|
| Pi=P(X=Xi)
| P0
| P1
| P2
| …
| Pk
|
|
Особое место среди случайных дискретных величин занимают величины с биномиальным законом распределения:
- число наступлений события в независимых повторных испытаниях,
- частота наступлений события в независимых повторных испытаниях.
Характеристики дискретной случайной величины:
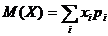 - математическое ожидание. (математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.)
- математическое ожидание. (математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.)
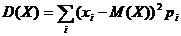 - дисперсия. (В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины)
- дисперсия. (В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины)
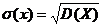 - среднее квадратическое отклонение. (Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение.)
- среднее квадратическое отклонение. (Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение.)
При расчетах дисперсии используют свойство: D(X) = М(Х2)-М2(Х).
Для биномиально распределенных случайных величин можно применять известные формулы расчета характеристик:
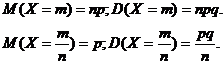
Функция распределения дискретной случайной величины: 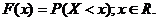
Функция распределения дискретной случайной величины является кусочно-постоянной, она имеет разрывы в точках с координатами, равными значениям случайной величины.
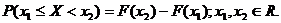
Основные операции над случайными дискретными величинами:
1. Умножение случайной величины на число a:
Y=aX, Y=yi=ахi,P(Y = уi)=P(X=xi)=pi;
где X=xi, P(X=xi)=pi
2. Суммирование случайных величин:
Z=X+Y, Z = zij=xi+yj, P(Z=zij)=pi*pj;
где Х = хi, Р(Х = xi)= pi; Y = yj, P(Y=yj)=pj
3. Умножение случайных величин:
Z = XY, Z = zij=xi*yj, P(Z=zij)=pi*pj;
где Х = хi, Р(Х = xi)= pi; Y = yj, P(Y=yj)=pj.
Пример 4.1. У господина "N" имеется три пакета акций различных предприятий. Вероятность получения дохода по пакету акций равна 0,6. Составить закон распределения случайной величины X - числа доходных пакетов акций у господина, определить ее математическое ожидание и дисперсию. Найти вероятность того, что у данного господина не менее двух доходных пакетов акций.
Решение. Для каждого выбранного пакета акций может наступить одно из событий: он не принесет дохода - 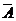 или принесет - А, по условию задачи с вероятностями Р(А)=0,6 = р; Р(
или принесет - А, по условию задачи с вероятностями Р(А)=0,6 = р; Р(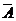 )=0,4 = q. Вероятности событий неизменны для всех пакетов акций, следовательно, имеют место независимые повторные испытания, число которых мало n=3.
)=0,4 = q. Вероятности событий неизменны для всех пакетов акций, следовательно, имеют место независимые повторные испытания, число которых мало n=3.
X – случайная величина, а именно, число доходных пакетов акций у господина. Рассмотрим событие хm=m, состоящее в том, что событие А наступит в n независимых испытаниях m раз. Для определения вероятности данного события следует применять формулу Бернулли. Случайная величина имеет биномиальный закон распределения:
Характеристики биномиально распределенной случайной величины можно найти, используя известные формулы:
Математическое ожидание - М(Х=m) =3*0,6=1,8.
Дисперсия – D(X=m) =3*0,6*0,4 = 0,72.
СобытиеВ, состоящее в том, что у господина не менее двух доходных пакетов акций, т.е. или два или три, имеет вероятность:
Р(В) = Р(Х ³2) = P(X= 2)+Р(Х = 3) = 0,432 +0,216 = 0,648.
Пример 4.2. В населенном пункте три рынка. Вероятность того, что на рынке есть необходимый для господина N товар, равна 0,6. Он пытается купить этот товар. Если на очередном рынке отсутствует данный товар, господин отправляется за ним на следующий рынок. Поиски прекращаются либо с приобретением товара, либо после того как посещены все рынки. Составить закон распределения числа посещенных рынков. Построить функцию распределения найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа посещенных рынков.
Решение. X - число посещенных рынков. Аi - событие, состоящее в том, что на посещенном рынке есть необходимый товар, 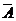 i- товар отсутствует. Вероятности этих событий: P(Аi)=0,6=p; P(
i- товар отсутствует. Вероятности этих событий: P(Аi)=0,6=p; P(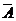 i)=0,4=q; i=1;2;3. Закон распределения и рабочие расчеты по характеристикам случайной величины:
i)=0,4=q; i=1;2;3. Закон распределения и рабочие расчеты по характеристикам случайной величины:
| хi
| pi=Р(Х = хi)
| XiPi
| Xi2Pi
|
|
| pl=P(X=l) = P(Al) = 0,6
| 0,6
| 0,6
|
|
| p2 = Р(Х = 2)=Р(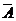 1)*Р(А2)=0,4*0,6 = 0,24 1)*Р(А2)=0,4*0,6 = 0,24
| 0,48
| 0,96
|
|
| p3 = Р(Х = 3)=Р(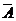 1)*Р( 1)*Р(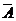 2)=0,4*0,4 = 0,16 2)=0,4*0,4 = 0,16
| 0,48
| 1,44
|
| å
| 1.0
| 1,56
| 3,0
|
Характеристики случайной величины - числа посещенных рынков:
Математическое ожидание - 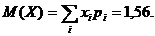
Дисперсия - D(X) = М(Х2)-М2(Х)=3-(1,56)2=0,5664.
Среднее квадратическое отклонение - 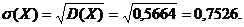
По определению функция распределения случайной величины: F(x)=P(X<x); xÎR.
Следовательно, функция распределения рассматриваемой случайной величины - числа доходных акций господина принимает вид:
|
| 0;
| x£1
|
| F(X)=
| p1=0,6;
| 1<х£2
|
|
| p1+ p2 = 0,6+0,24=0,84;
| 2<x£3
|
|
| p1+ p2+ p3=0,6+0,24+0,16 = 1;
| х>3
|
Пример 4.3. Найти закон распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины Z - суммы потраченных средств на приобретение товара, если известны законы распределения случайных величин Х - количества приобретаемого товара и Y - стоимости одной условной единицы товара. С какой вероятностью можно ожидать, что потраченные средства не превысят 1 условной единицы?
| Xi
| 0,3
| 0,4
| итого
|
| yj
|
|
|
| итого
|
| Pi
| 0,2
| 0,8
|
|
| Pj
| 0,3
| 0,5
| 0,2
|
|
Решение. Используем операцию умножения случайных величин. Рабочие расчеты по операции:
| yj
| Pj
|
|
|
|
| Xi
| Pi
| 0,3
| 0,5
| 0,2
|
| 0,3
|
| 0,3*2 = 0,6
| 0,3*3=0,9
| 0,3*4 = 1,2
|
|
| 0,2
| 0,2* 0,3 = 0,06
| 0,2 *0,5 = 0,1
| 0,2 * 0,2 = 0,04
|
| 0,4
|
| 0,4*2=0,8
| 0,4*3=1,2
| 0,4*4=1,6
|
|
| 0,8
| 0,8* 0,3 = 0,24
| 0,8* 0,5 = 0,4
| 0,8 * 0,2=0,16
|
Искомый закон распределения (первые две строки таблицы) и рабочие расчеты по характеристикам случайной величины Z - суммы потраченных средств:
| zij
| 0,6
| 0,8
| 0,9
| 1,2
| 1,6
| итого
|
| P(Z=zij)
| 0,06
| 0,24
| 0,1
| 0,4+0,04
| 0,16
|
|
| ZkPk
| 0,036
| 0,192
| 0,09
| 0,528
| 0,256
| 1,102
|
| Zk2Pk
| 0,0216
| 0,1536
| 0,081
| 0,6336
| 0,4096
| 1,2994
|
Математическое ожидание – M(Z) = åzкрк=1,102.
Дисперсия - D(Z)=m(z2)-M2(z)=1,2994-(1,102)2=0,085.
Среднее квадратическое отклонение - s(Z) = 0,291.
Вероятность того, что потраченные средства не превысят 1 условнойединицы:
P(Z<1)=0,06+0,24+0,1=0,4.
Пример 4.4. В урне 10 шаров: 4 белых, остальные – черные. Найти закон распределения случайной величины Х – числа белых шаров, если из урны один за одним не глядя вынули 3 шара. Найти математическое ожидание и дисперсию случайной величины Х. Найти вероятность того, что число вынутых белых шаров окажется больше математического ожидания.
Решение. Х – число белых шаров из 3 взятых. Закон распределения и рабочие расчеты по характеристикам случайной величины:
| хi
| pi=Р(Х = хi)
| XiPi
| Xi2Pi
|
|
| 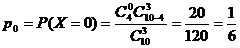
|
|
|
|
| 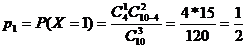
| 0,5
| 0,5
|
|
| 
| 0,6
| 1,2
|
|
| 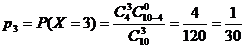
| 0,1
| 0,3
|
| å
| 1.0
| 1,2
| 2,0
|
Характеристики случайной величины Х - числа белых шаров из 3 взятых:
Математическое ожидание - 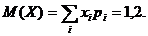
Дисперсия - D(X) = М(Х2)-М2(Х)=2-(1,2)2=0,56.
Вероятность того, что число вынутых белых шаров окажется больше математического ожидания:
P(X>M(X))=P(X>1,2)=P(X=2)+P(X=3)=0,3+1/30=1/3.
Закон распределения дискретной случайной величины Х в данной задаче носит название гипергеометрический закон распределения.
Непрерывная случайная величина (НСВ). Функция распределения и плотность вероятности НСВ. Числовые хар-ки НСВ. Равномерное распределение НСВ. Нормальный закон распределения, его параметры. Вероятность попадания НСВ в интервал.
Непрерывной случайной величиной называется случайная величина, все возможные значения которой целиком заполняют некоторый промежуток на числовой прямой.
Функция распределения непрерывной случайной величины: 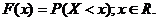
Функция не убывает и непрерывна, причем производная функции не имеет разрывов на всей числовой оси, за исключением конечного числа точек.
F(-¥)=0; F(+¥)=1.
Вероятность попадания случайной величины Х в интервал a£X<b определяется по формуле: P(a£X<b)=F(b)-F(a).
Плотность вероятности непрерывной случайной величины: f(x)=F’(x); xÎR.
Свойства плотности вероятности:
1. f(x)³0; xÎR.
2. 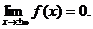
3. 
4. P(a£X<b)=F(b)-F(a)= 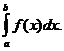
5. 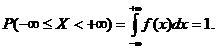
6. Математическое ожидание непрерывной случайной величины:
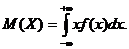
7. Дисперсия непрерывной случайной величины:
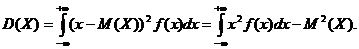
Нормальный закон распределения случайной величины.
Плотность вероятности: 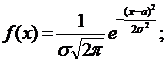 xÎR.
xÎR.
Параметры нормального закона:
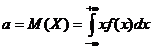 - математическое ожидание,
- математическое ожидание,
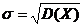 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Интегральная функция:
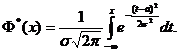
Свойства интегральной функции нормального закона:
1. F*(-¥)=0; F*(+¥)=1.
2. F*(x)=0,5+F(x), где F(x) – функция Лапласа.
3. F*(-x)=1-F*(x).
4. 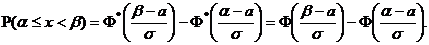
5. 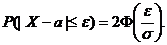
Сумма конечного числа независимых величин с нормальным законом распределения имеет нормальный закон распределения.
Важное применение для решения задач имеет теорема Ляпунова, согласно которой сумма большого количества независимых случайных непрерывных величин распределена по нормальному закону.
Равномерный закон распределения случайной величины.
Непрерывная случайная величина Х называется равномерно распределенной в интервале (a;b), если ее плотность распределения в этом интервале постоянна:
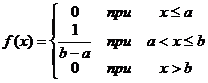
Интегральная функция:

Вероятность попадания в заданный интервал (a;b):
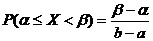
Математическое ожидание: 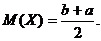
Дисперсия: 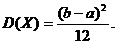
Среднее квадратическое отклонение: 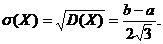
Показательный закон распределения случайной величины.
Плотность вероятности: 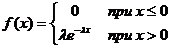
Параметр показательного закона: l - в теории массового обслуживания – среднее число событий, приходящихся на единицу времени.
Интегральная функция: 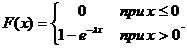
Вероятность попадания случайной величины в заданный интервал (a;b):
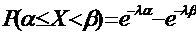
Математическое ожидание: 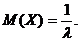
Дисперсия: 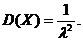
Среднее квадратическое отклонение: 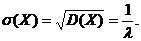
При определенных условиях число событий, произошедших за промежуток времени t, распределено по закону Пуассона с математическим ожиданием а=lt. Длина промежутка t, между произвольными двумя соседними событиями, подчиняется показательному закону: 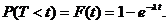
Пример 5.1. Дана плотность вероятности случайной величины X:
[ 0, x£l
[ f(X)= 0,25, 1<х£5. Найти функцию распределения, М(Х), D(X).
[ 0, х>5
Решение. По определению функция распределения F(x)= 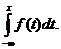
Следовательно, функция распределения принимает вид:
|
|
| x£1
|
| F(X)=
| 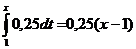
| 1<х£5
|
|
|
| х>5
|
Математическое ожидание случайной величины:
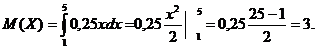
Дисперсия случайной величины:
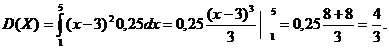
Пример 5.2. Торговая точка имеет в продаже большое количество различных товаров. Средняя выручка в день составляет 5 д.е., а среднее квадратическое отклонение 0.9 д.е. Составить плотность вероятности и функцию распределения выручки торговой точки. Найти вероятность того, что выручка торговой точки в случайно выбранный день: а) составит от 4 до 7 д.е., б) будет отличаться от средней выручки не более чем на 2 д.е.
Решение. X - выручка торговой точки, случайная величина, представляющая собой сумму большого количества случайных величин - выручек от продажи различных товаров, т.о., согласно теореме Ляпунова, имеет нормальный закон распределения.
Средняя выручка, по теории выборки (математическая статистика), является хорошей оценкой математического ожидания данной случайной величины. Следовательно: М(X)=5д.е.; s(Х)=0,9д.е.
Плотность вероятности - 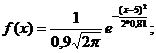 xÎR.
xÎR.
Функция распределения - 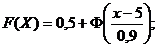 xÎR.
xÎR.
Вероятность того, что выручка торговой точки составит от 4 до 7 д.е.:
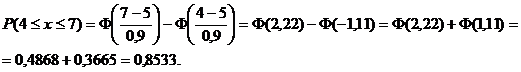
Вероятность того, что выручка будет отличаться от средней выручки не более чем на 2 д.е.:
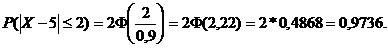
Пример 5.3. Автобусы некоторого маршрута идут строго по расписанию с интервалом движения 20 минут. Найти вероятность того, что пассажир, случайно подошедший к остановке, будет ожидать очередной автобус более 15 минут. Найти числовые характеристики полученной случайной величины.
Решение. Х- случайная величина, время ожидания пассажиром очередного автобуса. Случайная величина Х равномерно распределена в интервале (0;20].
a=0; b=20; a=15; b=20.
Плотность вероятности: 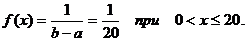
Вероятность ожидания автобуса более 15 минут:
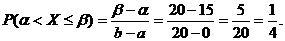
Математическое ожидание: 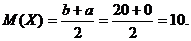
Дисперсия: 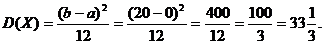
Среднее квадратическое отклонение: 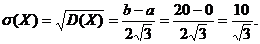
Пример 5.4. Случайная величина Х – время безотказной работы прибора распределена по показательному закону с параметром l=0,01 1/час. Вышедший из строя прибор немедленно заменяют новым. Найти вероятность того, что неисправность прибора наступит не ранее, чем через 150 часов. Найти вероятность того, что за 200 часов прибор не придется заменять.
Решение. Случайная величина Х – время безотказной работы прибора распределена по показательному закону, следовательно:
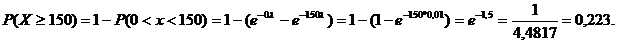
Число отказов прибора за время t=200 часов распределено по закону Пуассона с математическим ожиданием а= lt=0,01*200=2. Вероятность того, что за 200 часов прибор не придется заменять, вычисляется по формуле Пуассона:




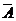 ) = 1-p = q.
) = 1-p = q.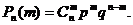
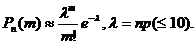
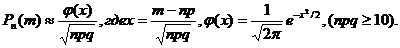
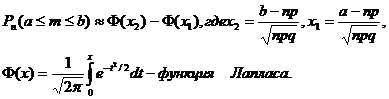
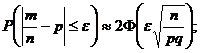
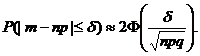
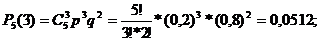
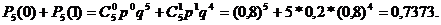
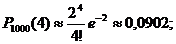
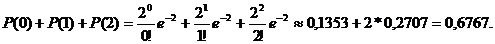
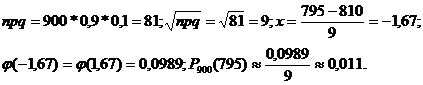
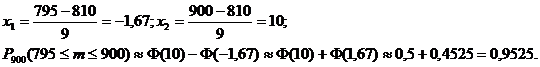
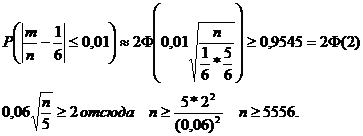
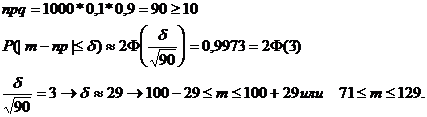
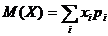 - математическое ожидание. (математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.)
- математическое ожидание. (математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.)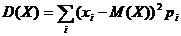 - дисперсия. (В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины)
- дисперсия. (В качестве меры рассеивания случайной величины используют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, которое называют дисперсией случайной величины)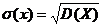 - среднее квадратическое отклонение. (Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение.)
- среднее квадратическое отклонение. (Кроме дисперсии для характеристики рассеяния значений признака генеральной (выборочной) совокупности вокруг своего среднего значения используют сводную характеристику — среднее квадратическое отклонение.)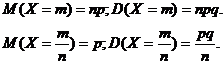
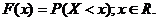
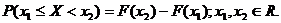
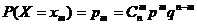
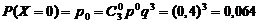
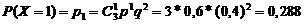
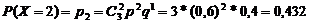
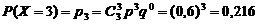
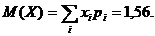
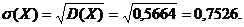
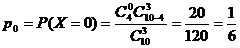
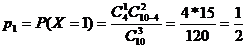

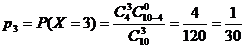
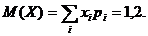
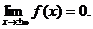

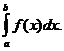
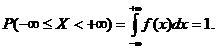
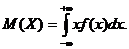
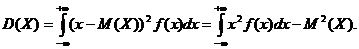
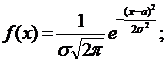 xÎR.
xÎR.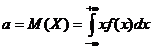 - математическое ожидание,
- математическое ожидание,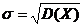 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.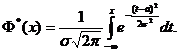
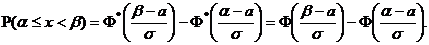
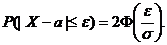
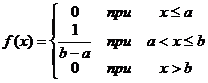

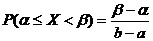
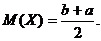
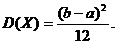
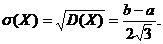
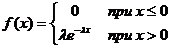
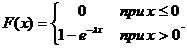
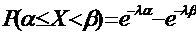
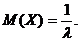
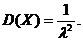
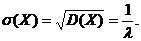
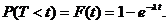
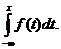
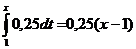
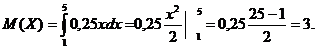
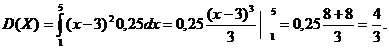
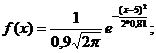 xÎR.
xÎR.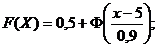 xÎR.
xÎR.