Теорема об изменении кинетической энергии системы: в дифференциальной форме: dT =  ,
,  ,
,  – элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:Т2 – Т1=
– элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:Т2 – Т1=  . Для неизменяемой системы
. Для неизменяемой системы  и Т2 – Т1=
и Т2 – Т1=  , т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд):
, т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд):  < 1, Апол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), Азатр= Апол.сопр.+ Авр.сопр. – затраченная работа, Авр.сопр.-– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.). h= Nмаш/Nдв, Nмаш – полезная мощность машины, Nдв – мощность дв-ля, приводящего ее в движение. Закон сохранения полной механической энергии: Т + П = const. Если система движется под действием потенциальных сил, то сумма кинетической и потенциальной энергий сохраняет постоянное значение. (Т + П — интеграл энергии). Потенциальные силы – силы, работа которых не зависит от вида траектории, по которой перемещается точка (пр.: сила тяжести, сила упругости). Непотенциальные – напр.: силы трения. Механическая энергия – сумма кинетической и потенциальной энергий. Расход механической энергии обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию.
< 1, Апол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), Азатр= Апол.сопр.+ Авр.сопр. – затраченная работа, Авр.сопр.-– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.). h= Nмаш/Nдв, Nмаш – полезная мощность машины, Nдв – мощность дв-ля, приводящего ее в движение. Закон сохранения полной механической энергии: Т + П = const. Если система движется под действием потенциальных сил, то сумма кинетической и потенциальной энергий сохраняет постоянное значение. (Т + П — интеграл энергии). Потенциальные силы – силы, работа которых не зависит от вида траектории, по которой перемещается точка (пр.: сила тяжести, сила упругости). Непотенциальные – напр.: силы трения. Механическая энергия – сумма кинетической и потенциальной энергий. Расход механической энергии обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию.
25.Принцип Даламбера.
Пусть мы имеем систему, состоящих из n материальных точек. Выделим какую-нибудь из точек системы с массой  . Под действием приложенных к ней внешних и внутренних сил
. Под действием приложенных к ней внешних и внутренних сил  и
и  (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение  .Введем в рассмотрение величину
.Введем в рассмотрение величину  , имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции). Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам
, имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции). Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам  и
и  прибавить силу инерции
прибавить силу инерции  , то полученная система сил будет уравновешенной, т.е. будет
, то полученная система сил будет уравновешенной, т.е. будет  . Это выражение выражает принцип Даламбера для одной материальной точки. оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает
. Это выражение выражает принцип Даламбера для одной материальной точки. оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает  . Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и, возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют. Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систему. Тогда на основании принципа Даламбера должно быть:
. Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и, возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют. Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систему. Тогда на основании принципа Даламбера должно быть: 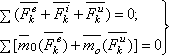
Введём обозначения: 
 Величины
Величины  и
и 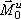 представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:  (1) Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил. В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.
(1) Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил. В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.



 ,
,  ,
,  – элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:Т2 – Т1=
– элементарные работы, действующих на точку внешних и внутренних сил, в конечной форме:Т2 – Т1=  . Для неизменяемой системы
. Для неизменяемой системы  и Т2 – Т1=
и Т2 – Т1=  , т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд):
, т.е. изменение кинетической энергии твердого тела на некотором перемещении равно сумме работ внешних сил, действующих на тело на этом перемещении. Если сумма работ реакций связей на любом возможном перемещении системы равна нулю, то такие связи называются идеальными. Коэффициент полезного действия (кпд):  < 1, Апол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), Азатр= Апол.сопр.+ Авр.сопр. – затраченная работа, Авр.сопр.-– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.). h= Nмаш/Nдв, Nмаш – полезная мощность машины, Nдв – мощность дв-ля, приводящего ее в движение. Закон сохранения полной механической энергии: Т + П = const. Если система движется под действием потенциальных сил, то сумма кинетической и потенциальной энергий сохраняет постоянное значение. (Т + П — интеграл энергии). Потенциальные силы – силы, работа которых не зависит от вида траектории, по которой перемещается точка (пр.: сила тяжести, сила упругости). Непотенциальные – напр.: силы трения. Механическая энергия – сумма кинетической и потенциальной энергий. Расход механической энергии обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию.
< 1, Апол.сопр. – работа полезных сил сопротивления (сил, для которых предназначена машина), Азатр= Апол.сопр.+ Авр.сопр. – затраченная работа, Авр.сопр.-– работа вредных сил сопротивления (силы трения, сопротивления воздуха и т.п.). h= Nмаш/Nдв, Nмаш – полезная мощность машины, Nдв – мощность дв-ля, приводящего ее в движение. Закон сохранения полной механической энергии: Т + П = const. Если система движется под действием потенциальных сил, то сумма кинетической и потенциальной энергий сохраняет постоянное значение. (Т + П — интеграл энергии). Потенциальные силы – силы, работа которых не зависит от вида траектории, по которой перемещается точка (пр.: сила тяжести, сила упругости). Непотенциальные – напр.: силы трения. Механическая энергия – сумма кинетической и потенциальной энергий. Расход механической энергии обычно означает превращение ее в теплоту, электричество, звук или свет, а приток механической энергии связан с обратным процессом превращения различных видов энергии в механическую энергию. . Под действием приложенных к ней внешних и внутренних сил
. Под действием приложенных к ней внешних и внутренних сил  и
и  (в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение
(в которые входят и активные силы, и реакции связи) точка получает по отношению к инерционной системе отсчета некоторое ускорение  .Введем в рассмотрение величину
.Введем в рассмотрение величину  , имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции). Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам
, имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки(иногда даламберовой силой инерции). Тогда оказывается, что движение точки обладает следующим общим свойством: если в каждый момент времени к фактически действующим на точку силам  , то полученная система сил будет уравновешенной, т.е. будет
, то полученная система сил будет уравновешенной, т.е. будет  . Это выражение выражает принцип Даламбера для одной материальной точки. оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает
. Это выражение выражает принцип Даламбера для одной материальной точки. оно эквивалентно второму закону Ньютона и наоборот. В самом деле, второй закон Ньютона для рассматриваемой точки дает  . Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и, возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют. Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систему. Тогда на основании принципа Даламбера должно быть:
. Значение принципа Даламбера состоит в том, что при непосредственном его применении к задачам динамики уравнения движения системы составляются в форме хорошо известных уравнений равновесия; что делает единообразный подход к решению задач и обычно намного упрощает соответствующие расчёты. Применяя принцип Даламбера, следует иметь в виду, что на точку механической системы, движение которой изучается, действуют только внешние и внутренние силы и, возникающие в результате взаимодействия точек системы друг с другом и с телами, не входящими в систему; под действием этих сил точки системы и движутся с соответствующими ускорениями. Силы же инерции, о которых говорится в принципе Даламбера, на движущиеся точки не действуют. Из статики известно, что геометрическая сумма сил, находящихся в равновесии, и сумма их моментов относительно любого центра О равны нулю, причём по принципу отвердевания это справедливо для сил, действующих не только на твёрдое тело, но и на любую изменяемую систему. Тогда на основании принципа Даламбера должно быть: 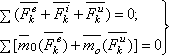

 Величины
Величины  и
и 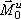 представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:
представляют собой главный вектор и главный момент относительно центра О системы сил инерции. В результате, учитывая, что геометрическая сумма внутренних сил и сумма их моментов равны нулю, получим из равенств:  (1) Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил. В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.
(1) Применение уравнений (1), вытекающих из принципа Даламбера, упрощает процесс решения задач, т.к. эти уравнения не содержат внутренних сил. В проекциях на оси координат эти равенства дают уравнения, аналогичные соответствующим уравнениям статики. Чтобы пользоваться этими уравнениями при решении задач, надо знать выражение главного вектора и главного момента сил инерций.

