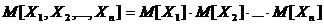Часто возникает необходимость определить не характеристики случайных величин или их законы распределения, а характеристики функции от случайных аргументов.
Любая функция от случайных аргументов является также случайной величиной, свойства которой определяются характеристиками случайных величин – такими как закон распределения, математическое ожидание, дисперсия и другие начальные и центральные моменты.
Для определения числовых характеристик функции от случайных аргументов достаточно знать законы распределения этих случайных аргументов.
Пусть задана функция Y = φ(X), при этом Х – случайная величина с известным законом распределения. Пусть х является дискретной случайной величиной с заданным рядом распределения
| Х
| х 1
| х 2
| ...
| х n
|
| Y
| Р 1
| Р 2
| ...
| Р n
|
Рассмотрим ряд вида:
| Y
| φ(х 1)
| φ(х 2)
| ...
| φ(х n)
|
| P i
| P 1
| P 2
| ...
| P n
|
В общем случае этот ряд не является рядом распределения величины Y, так как в нём могут повторяться значения функции φ(х i).
Однако с помощью этого ряда можно определить числовые характеристики величины Y:
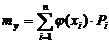
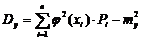
Если случайная величина непрерывна, то соответствующие характеристики определяются по формулам:
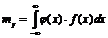
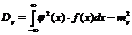
где f (x) – плотность распределения случайной величины Х.
Если функция зависит от совокупности аргументов, т.е. 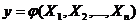 , где
, где  - система случайных величин, то математическое ожидание и дисперсия этой функции будет определяться по формулам:
- система случайных величин, то математическое ожидание и дисперсия этой функции будет определяться по формулам:
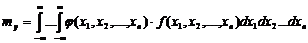
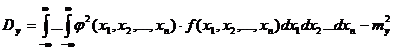
где 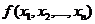 - плотность распределения системы.
- плотность распределения системы.
В тех случаях, когда функция y является линейной функцией от случайных аргументов, то её числовые характеристики могут быть определены по числовым характеристикам случайных аргументов.
Числовые характеристики линейных функций от случайных аргументов определяются по теоремам о числовых характеристиках функции от случайных аргументов.
Билет
"Т1" Пусть У = С (с – const). Тогда математическое ожидание случайной величины У равняется этой константе, то есть справедлива формула:
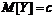
"Т2" Дисперсия постоянной величины равняется 0: 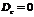
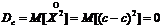
"Т3" Пусть функция 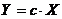 - это произведение неслучайной величины на случайную. Тогда математическое ожидание произведения неслучайной величины на случайную равняется произведению неслучайной величины на математическое ожидание случайной величины, т.е.:
- это произведение неслучайной величины на случайную. Тогда математическое ожидание произведения неслучайной величины на случайную равняется произведению неслучайной величины на математическое ожидание случайной величины, т.е.:
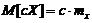
Доказательство: Рассмотрим случай дискретной случайной величины: 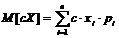
Согласно свойствам суммы, постоянную можно вынести за знак суммы:
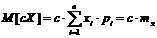
"Т4" Дисперсия произведения неслучайной величины на случайную равняется произведению квадрата неслучайной величины на дисперсию случайной величины, т.е.:
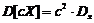
Доказательство: Дисперсию произведения можно представить в виде:
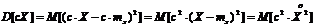
Согласно теореме о математическом ожидании произведения неслучайной величины на случайную, данное выражение можно записать в виде:
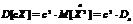
"Т5" Пусть дана функция 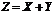 , равная сумме двух случайных величин. Тогда математическое ожидание суммы двух случайных величин равняется сумме их математических ожиданий, т.е.:
, равная сумме двух случайных величин. Тогда математическое ожидание суммы двух случайных величин равняется сумме их математических ожиданий, т.е.: 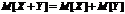
Доказательство: Рассмотрим систему двух дискретных случайных величин с известным законом распределения. Тогда математическое ожидание суммы двух случайных величин можно представить в виде:
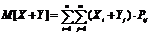 ,
,
где 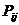 - это вероятность того, что сумма (X +Y) примет значения i и j.
- это вероятность того, что сумма (X +Y) примет значения i и j.
На основании свойств суммы данное выражение можно записать в виде:
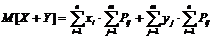 .
.
Если учесть, что 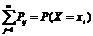 , а
, а 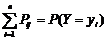 , то математическое ожидание суммы можно заменить выражением вида:
, то математическое ожидание суммы можно заменить выражением вида:
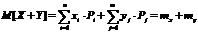 , что и требовалось доказать.
, что и требовалось доказать.
"Т6" Пусть дана функция  . Тогда дисперсия суммы двух случайных величин будет равна сумме дисперсий этих случайных величин плюс удвоенное произведение корелляционного момента между этими случайными величинами, т.е.:
. Тогда дисперсия суммы двух случайных величин будет равна сумме дисперсий этих случайных величин плюс удвоенное произведение корелляционного момента между этими случайными величинами, т.е.:

Доказательство: Представим центрированную случайную величину  в виде:
в виде:
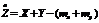
Согласно определению дисперсии случайной величины, дисперсию случайных величин 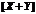 можно представить как математическое ожидание квадрата центрированной случайной величины
можно представить как математическое ожидание квадрата центрированной случайной величины 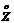 :
:
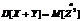 или:
или: 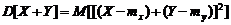
а так как 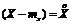 , а
, а 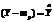 , то:
, то: 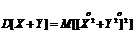
Представим правую часть данного выражения в виде:
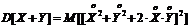
На основании теоремы о математическом ожидании суммы случайных величин можно записать, что дисперсия суммы равняется:
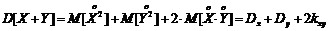 , что и требовалось доказать.
, что и требовалось доказать.
"Т7" Математическое ожидание произведения двух случайных величин равняется произведению их математических ожиданий плюс корелляционный момент между ними.
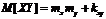
Доказательство: Известно, что корелляционный момент между двумя случайными величинами равен математическому ожиданию произведения центрированных случайных величин: 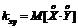
Запишем данное выражение в виде:
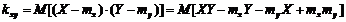
На основании теоремы о математическом ожидании суммы:
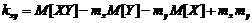
Следовательно, 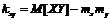 и
и 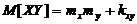 , что и требовалось доказать.
, что и требовалось доказать.
Очевидно, если случайные величины некореллированы, то математическое ожидание произведения этих случайных величин равняется произведению их математических ожиданий:
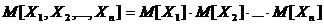



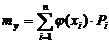
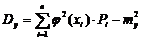
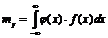
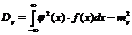
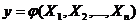 , где
, где  - система случайных величин, то математическое ожидание и дисперсия этой функции будет определяться по формулам:
- система случайных величин, то математическое ожидание и дисперсия этой функции будет определяться по формулам: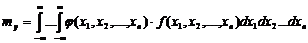
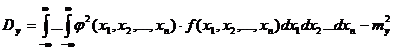
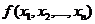 - плотность распределения системы.
- плотность распределения системы.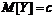
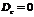
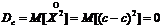
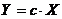 - это произведение неслучайной величины на случайную. Тогда математическое ожидание произведения неслучайной величины на случайную равняется произведению неслучайной величины на математическое ожидание случайной величины, т.е.:
- это произведение неслучайной величины на случайную. Тогда математическое ожидание произведения неслучайной величины на случайную равняется произведению неслучайной величины на математическое ожидание случайной величины, т.е.: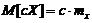
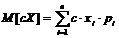
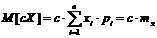
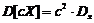
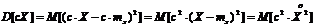
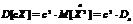
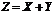 , равная сумме двух случайных величин. Тогда математическое ожидание суммы двух случайных величин равняется сумме их математических ожиданий, т.е.:
, равная сумме двух случайных величин. Тогда математическое ожидание суммы двух случайных величин равняется сумме их математических ожиданий, т.е.: 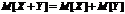
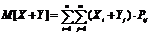 ,
,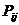 - это вероятность того, что сумма (X +Y) примет значения i и j.
- это вероятность того, что сумма (X +Y) примет значения i и j.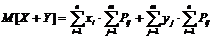 .
.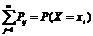 , а
, а 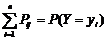 , то математическое ожидание суммы можно заменить выражением вида:
, то математическое ожидание суммы можно заменить выражением вида: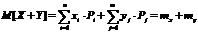 , что и требовалось доказать.
, что и требовалось доказать. . Тогда дисперсия суммы двух случайных величин будет равна сумме дисперсий этих случайных величин плюс удвоенное произведение корелляционного момента между этими случайными величинами, т.е.:
. Тогда дисперсия суммы двух случайных величин будет равна сумме дисперсий этих случайных величин плюс удвоенное произведение корелляционного момента между этими случайными величинами, т.е.:
 в виде:
в виде: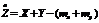
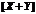 можно представить как математическое ожидание квадрата центрированной случайной величины
можно представить как математическое ожидание квадрата центрированной случайной величины 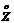 :
: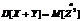 или:
или: 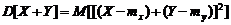
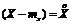 , а
, а 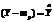 , то:
, то: 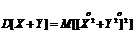
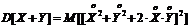
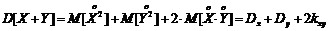 , что и требовалось доказать.
, что и требовалось доказать.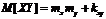
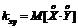
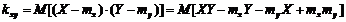
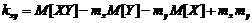
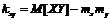 и
и 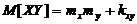 , что и требовалось доказать.
, что и требовалось доказать.