

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Равномерное распределение:
Непрерывная случайная величина имеет равномерное распределение на отрезке [a, b], если её плотность распределения задаётся выражением:
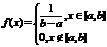
График этой плотности распределения имеет вид:
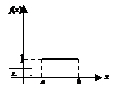
Функция распределения:
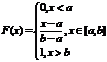
График функции распределения:

Числовые характеристики: 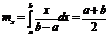
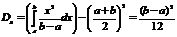 Вероятностная задача относительно этой непрерывной случайной величины решается по формуле:
Вероятностная задача относительно этой непрерывной случайной величины решается по формуле:
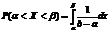 , a, bÎ[a, b]
, a, bÎ[a, b]
1) Показательное распределение:
Показательное распределение характеризует закон распределения интервала времени между двумя событиями в простейшем потоке.
Действительно, вероятность того, что за время τ не наступит очередное событие, согласно распределению Пуассона, можно задать выражением вида:
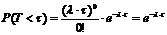 0! = 1
0! = 1
Соответственно, вероятность того, что за время τ наступит очередное событие, будет равна:
Р(Т > τ) = 1 – е-λ×τ (1)
Это выражение характеризует функцию распределения случайной величины. Если через Х обозначить случайную величину "время наступления очередного события", то выражение (1) можно записать в виде:
Р(Х > х) = 1 – е-λ× х (2)
С учётом этого, функцию распределения случайной величины, имеющей показательное распределение, можно записать следующим образом:
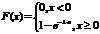
Числовые характеристики:
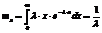
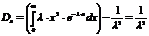
Вероятностная задача определяется:
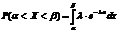
Показательное распределение играет исключительную роль в теории надёжности. Через показательное распределение задаётся так называемая функция надёжности, имеющая вид:
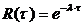
где 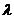 – интенсивность отказов (среднее число отказов в единицу времени),
– интенсивность отказов (среднее число отказов в единицу времени),
а функция надёжности определяет вероятность того, что в течение времени τ то или иное устройство будет работать безотказно.
|
|
2) Нормальное распределение:
Нормальный закон распределения случайной величины является основным законом природы, где процесс описывается с помощью случайной величины.
Плотность распределения случайной величины, имеющей нормальное распределение, задаётся выражением:
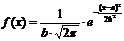
где a и b – параметры распределения.
Математическое ожидание:
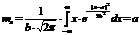
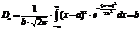
Из этого следует, что среднее квадратичное случайной величины по нормальному закону sх равна параметру b данного распределения.
Как правило, при решении вероятностных задач относительно случайной величины, распределённой по нормальному закону, вводится такое понятие как нормальное стандартное распределение.
В этом распределении математическое ожидание равно 0 (mх = 0), дисперсия равна 0 (D х = 0), следовательно, sх = 0.
Плотность распределения:
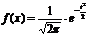
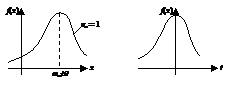
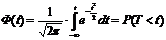
Для функции стандартного нормального распределения:
составляются таблицы.
Для того, чтобы через стандартное нормальное распределение можно было решить вероятностную задачу относительно случайной величины общего вида, то есть когда mх ≠0 и D х ≠0, её центрируют (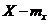 ) и нормируют (÷
) и нормируют (÷ 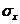 ) таким образом:
) таким образом: 
В этом случае случайная величина Т имеет стандартное нормальное распределение. И тогда связь между функциями распределения случайной величины общего вида и функцией распределения стандартной величины задаётся выражением:
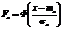
Соответственно, вероятность того, что случайная величина Х больше a и меньше b, равна:
Р (a<Х<b) = F(b) – F(a) = 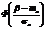 -
- 
Системы случайных величин
На практике случайные явления чаще всего можно характеризовать не одной случайной величиной, а совокупностью случайных величин.
Как и отдельная случайная величина, свойство системы случайных величин определяется её характеристиками – такими как законы распределения системы случайных величин и числовые характеристики (как характеристиками отдельных случайных величин, входящих в систему, так и характеристиками, отражающими связь между случайными величинами, входящими в систему.Бывают системы как дискретных, так и непрерывных случайных величин.
|
|
Закон распределения систему двух случайных величин можно задать в виде таблицы:
| Х | Y | |||||
| y1 | y2 | … | yi | … | ym | |
| x 1 | Р11 | Р12 | ... | Р1i | ... | Р1m |
| x 2 | Р21 | Р22 | ... | Р2i | ... | Р2m |
| ... | ... | ... | ... | ... | ... | … |
| x i | Рi1 | Рi2 | ... | Рij | ... | Рim |
| ... | ... | ... | ... | ... | ... | … |
| x n | Рn1 | Рn2 | ... | Рnj | ... | Рnm |
Где 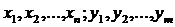 – возможные значения случайных величин
– возможные значения случайных величин 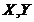 , которые могут быть приняты в результате опыта;
, которые могут быть приняты в результате опыта;
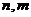 – число возможных значений соответственно случайных величин Х, Y;
– число возможных значений соответственно случайных величин Х, Y;
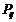 – вероятность того, что случайная величина Х примет значение x i, а Y – yi.
– вероятность того, что случайная величина Х примет значение x i, а Y – yi.
Закон распределения системы случайных величин является её полной характеристикой. Зная закон распределения системы случайных величин, можно определить законы распределения отдельных случайных величин, входящих в систему, а также числовые характеристики этих случайных величин.
Так как случайная величина Х может принять значение x i при одном из несовместных событий, а именно при Y примет значение y1, Y примет значение y2, то вероятность этого равна: 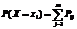
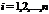 Аналогично для случайной величины Y определяется по формуле:
Аналогично для случайной величины Y определяется по формуле:
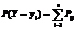
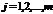
Характеристики каждой из случайных величин определяются по формуле: 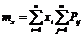
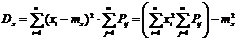
Аналогичным образом и для Y:
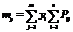

Важной характеристикой системы случайных величин является корелляционный момент между случайными величинами, входящими в систему. Эта характеристика отражает силу связи между случайными величинами и рассеивание случайных величин относительно математических ожиданий. Эта характеристика задаётся выражением:
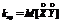
То есть корелляционный момент равен математическому ожиданию произведения центрированных случайных величин.
Для дискретной случайной величины эта характеристика определяется по формуле:

Корелляционный момент может быть вычислен:
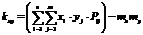
Для того, чтобы определить только силу связи между случайными величинами, вводится такая характеристика как коэффициент корелляции между случайными величинами, который задаётся выражением:

Где 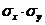 - СКО (средне квадратичное отклонение) случайных величин Х и Y.
- СКО (средне квадратичное отклонение) случайных величин Х и Y.
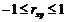
Если 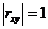 , то между случайными величинами существует линейная связь. Это значит, что по значению одной из случайных величин можно судить однозначно о значении другой случайной величины.
, то между случайными величинами существует линейная связь. Это значит, что по значению одной из случайных величин можно судить однозначно о значении другой случайной величины.
|
|
Если 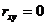 , то кореляционной связи между случайными величинами не существует.
, то кореляционной связи между случайными величинами не существует.
В качестве основных характеристик систему двух непрерывных случайных величин рассматриваются функция распределения системы случайных величин и плотность распределения.
Функция распределения системы двух непрерывных случайных величин определяется:
F(x, y) = P(X< x, Y<y)
То есть функция распределения равна вероятности того, что случайная точка попадёт в квадрат с вершинами (x, y).
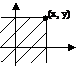
|
|
|

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!