Пример 5.1. Дана случайная величина 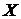 с математическим ожиданием
с математическим ожиданием 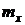 и дисперсией
и дисперсией 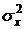 . Оценить сверху вероятность того, что величина
. Оценить сверху вероятность того, что величина 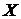 отклонится от своего математического ожидания не меньше, чем на
отклонится от своего математического ожидания не меньше, чем на 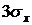 .
.
Решение. Полагая во втором неравенстве Чебышева 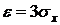 , получим
, получим
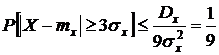 ,
,
т.е. вероятность того, что отклонение случайной величины от ее математического ожидания выйдет за пределы трех средних квадратических отклонений, не может быть больше 1/9 ни при каком законе распределения.
Замечание. На практике в большинстве случаев вероятность того, что величина 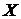 выйдет за пределы участка
выйдет за пределы участка 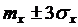 , значительно меньше 1/9. Например, для нормального закона эта вероятность приблизительно равна 0.003.
, значительно меньше 1/9. Например, для нормального закона эта вероятность приблизительно равна 0.003.
Пример 5.2. Среднее значение скорости ветра в данной местности равно 16 км/час. Оценить вероятность того, что в данной местности скорость ветра (при одном наблюдении) не превышает 80 км/час.
Решение. По первой форме неравенства Чебышева находим
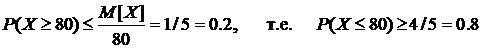 .
.
Пример 5.3. Математическое ожидание скорости ветра на данной высоте равно 25 км/час, а 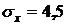 км/час. Какие скорости ветра можно ожидать на этой высоте с вероятностью не меньшей чем 0.9?
км/час. Какие скорости ветра можно ожидать на этой высоте с вероятностью не меньшей чем 0.9?
Решение. Пусть 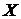 - скорость ветра. Тогда по второму неравенству Чебышева имеем
- скорость ветра. Тогда по второму неравенству Чебышева имеем 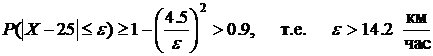 .
.
Следовательно, с вероятностью, большей 0.9, имеем 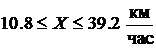 .
.
Пример 5.4. 4 станка производят детали из стали марки 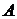 , 6 других – из стали марки
, 6 других – из стали марки 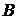 . Определить вероятность того, что из 500 взятых деталей количество деталей из стали марки
. Определить вероятность того, что из 500 взятых деталей количество деталей из стали марки 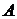 будет заключено в пределах от 180 до 220.
будет заключено в пределах от 180 до 220.
Решение. Воспользуемся неравенством Чебышева для оценки нижней границы искомой вероятности 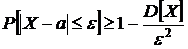 .
.
Имеем 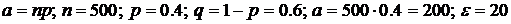 .
.
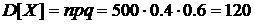 .
.
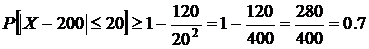 .
.
С другой стороны, эту вероятность можно более точно вычислить (оценить) по теореме Муавра–Лапласа:
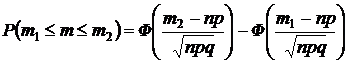 ,
,
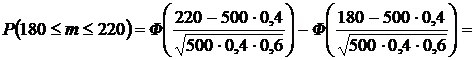
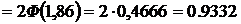 .
.
Пример 5.5. Станок–автомат требует подналадки в среднем один раз за 4 часа работы. Определить вероятность того, что за 10 суток непрерывной работы подналадка осуществлялась ровно 70 раз.
Решение. Имеем n = 240; m = 70; p = 0.25; q = 0.75.
По локальной теореме Муавра–Лапласа получаем
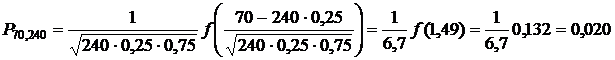 .
.
По закону Пуассона эта вероятность 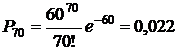 .
.
Пример 5.6. В страховой фирме застраховано 10 тысяч лиц одного возраста и одной социальной группы. Вероятность смерти в течение года для каждого лица равна 0,006. Каждый застрахованный в начале года вносит 12 долларов страховых, и, в случае смерти, его родственники получают от фирмы тысячу долларов. Найти вероятность того, что:
1) фирма потерпит убыток;
2) фирма получит прибыль, не меньшую чем x тысяч долларов 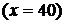 .
.
Решение. Вероятность убытков для страховой фирмы есть вероятность смерти в течении года более чем 120 застрахованных.
Тогда по формуле Муавра–Лапласа имеем
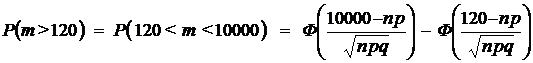 .
.
У нас 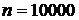 ;
; 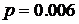 ;
; 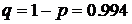 .
.
Тогда с точностью до 10 знаков после запятой
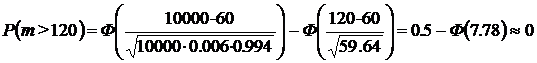 .
.
Получение прибыли в x тысяч долларов и более может быть, если в течении года из застрахованных умрёт не более чем 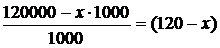 человек. В этом случае вероятность получения фирмой прибыли (П) не менее величины x равна:
человек. В этом случае вероятность получения фирмой прибыли (П) не менее величины x равна:
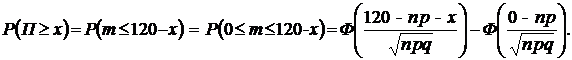
При 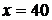 получим:
получим:
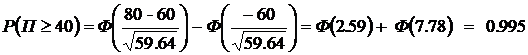 .
.
Пример 5.7. Три станка, производительности которых соотносятся как 5:3:2, производят детали на общий конвейер. Определить вероятность того, что из 240 деталей, взятых случайным образом с конвейера, деталей, произведенных вторым станком будет от 60 до 70.
Решение. Искомую вероятность определяем по интегральной формуле Муавра–Лапласа:
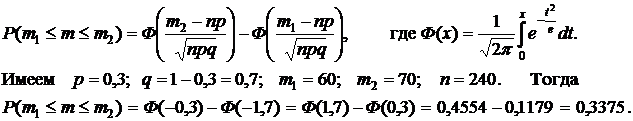
Пример 5.8. Вероятность изделию быть бракованным равна 0,05. Сколько изделий надо взять, чтобы с вероятностью не меньшей 0,9 среди них оказалось не менее 50 бракованных?
Решение. Необходимо найти число n, удовлетворяющее интегральной формуле Муавра–Лапласа
P (50 Ј m Ј n) = 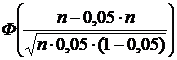 –
– 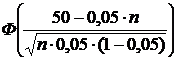 і 0,9.
і 0,9.
Оценим значение
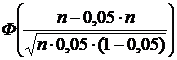 =
= 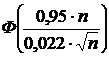 » Ф (4,3
» Ф (4,3 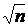 ) і Ф (30)» 0,5.
) і Ф (30)» 0,5.
Тогда 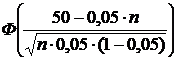 Ј – 0,4.
Ј – 0,4.
По таблице функции Лапласа находим, что Ф (х) = – 0,4 при х = 1,28.
Поэтому получаем соотношение 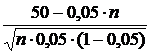 Ј 1,28
Ј 1,28
или 0,05 Чn – 0,282Ч 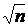 – 50 і 0.
– 50 і 0.
Решая последнее неравенство, находим n і 1196, то есть следует взять не менее 1196 изделий.



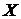 с математическим ожиданием
с математическим ожиданием 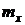 и дисперсией
и дисперсией 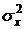 . Оценить сверху вероятность того, что величина
. Оценить сверху вероятность того, что величина 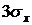 .
.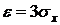 , получим
, получим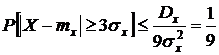 ,
,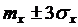 , значительно меньше 1/9. Например, для нормального закона эта вероятность приблизительно равна 0.003.
, значительно меньше 1/9. Например, для нормального закона эта вероятность приблизительно равна 0.003.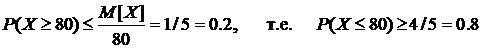 .
.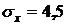 км/час. Какие скорости ветра можно ожидать на этой высоте с вероятностью не меньшей чем 0.9?
км/час. Какие скорости ветра можно ожидать на этой высоте с вероятностью не меньшей чем 0.9?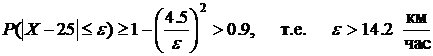 .
.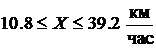 .
.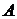 , 6 других – из стали марки
, 6 других – из стали марки 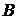 . Определить вероятность того, что из 500 взятых деталей количество деталей из стали марки
. Определить вероятность того, что из 500 взятых деталей количество деталей из стали марки 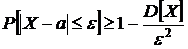 .
.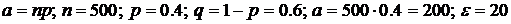 .
.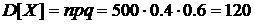 .
.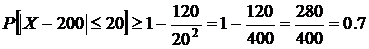 .
.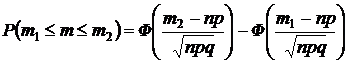 ,
,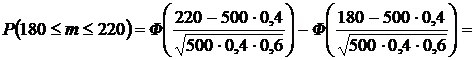
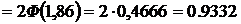 .
.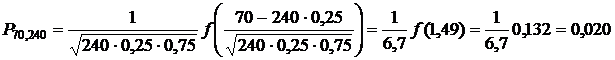 .
.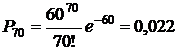 .
.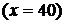 .
.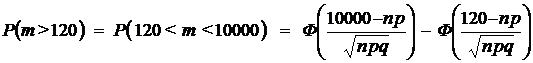 .
.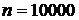 ;
; 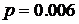 ;
; 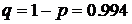 .
.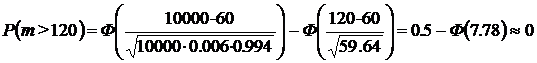 .
.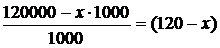 человек. В этом случае вероятность получения фирмой прибыли (П) не менее величины x равна:
человек. В этом случае вероятность получения фирмой прибыли (П) не менее величины x равна: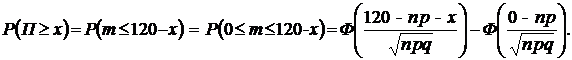
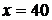 получим:
получим: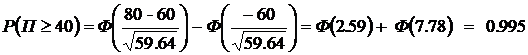 .
.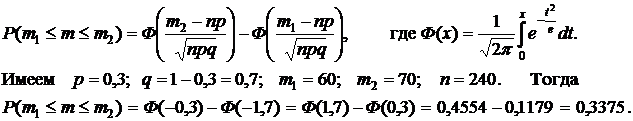
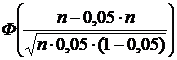 –
– 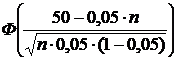 і 0,9.
і 0,9.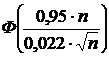 » Ф (4,3
» Ф (4,3 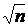 ) і Ф (30)» 0,5.
) і Ф (30)» 0,5.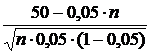 Ј 1,28
Ј 1,28


