Пример 3. Найти ортогональное преобразование, приводящее квадратичную форму
F = 11  + 5
+ 5  + 2
+ 2  + 16 x 1 x 2 + 4 x 1 x 3–20 x 2 x 3
+ 16 x 1 x 2 + 4 x 1 x 3–20 x 2 x 3
к каноническому виду, и написать этот канонический вид:
Р е ш е н и е. Матрица квадратичной формы имеет вид A =  .
.
Найдем собственные числа этой матрицы. Для этого запишем характеристическое уравнение:
| A – λE | =  = (11− λ) (5− λ) (2− λ) + 2⋅8⋅(−10) + 2⋅8⋅(−10) − 2⋅(5− λ)⋅2−(11− λ)·
= (11− λ) (5− λ) (2− λ) + 2⋅8⋅(−10) + 2⋅8⋅(−10) − 2⋅(5− λ)⋅2−(11− λ)·
⋅(−10)⋅(−10)−8⋅8⋅(2− λ) = − λ 3 + λ 2 (2+5+11) − λ (10+22+55) +110 −160 – 160 – 20 + 4 λ − 1100 + 100 λ –
–128 + 64 λ = − λ 3 +18 λ 2 + 81 λ −1458 = − λ (λ 2 − 81) + 18 (λ 2 − 81) = (λ − 9) (λ + 9) (− λ + 18) = 0.
Отсюда находим собственные числа: λ 1 = 9, λ 2 = −9, λ 3 = 18.
Далее находим собственные векторы:
Собственный вектор для собственного числа λ 1 = 9 найдем из системы  =>
=>

 ~
~ 

 ~
~ 
 ~
~ 
 ~
~ 
ð 
Решая данную систему, получим x 1 = x 3, x 2 = –  x 3.
x 3.
Фундаментальная система решений состоит из одного вектора  .
.
Соответствующий ортонормированный собственный вектор:
 =
=  => e 1 =
=> e 1 =  .
.
Собственный вектор для собственного числа λ 2 = –9 найдем из системы 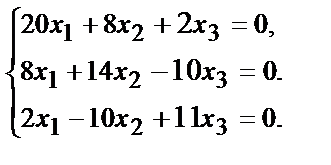

 ~
~ 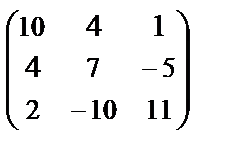

 ~
~ 
 ~
~ 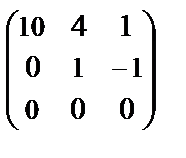
ð  Решая данную систему, получим x 1 = –
Решая данную систему, получим x 1 = –  x 3, x 2 = x 3.
x 3, x 2 = x 3.
Фундаментальная система решений состоит из одного вектора  .
.
Соответствующий ортонормированный собственный вектор:
 =
=  => e 2 =
=> e 2 =  .
.
Собственный вектор для собственного числа λ 3 = 18 найдем из системы 


 ~
~ 

 ~
~ 
 ~
~ 
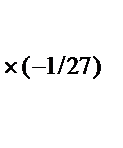 ~
~
~  =>
=> 
Решая данную систему, получим x 1 = –2 x 3, x 2 = –2 x 3.
Фундаментальная системарешений состоит из одного вектора  .
.
Соответствующий ортонормированный собственный вектор:
 = 3 => e 3 =
= 3 => e 3 =  .
.
Т.о., матрица S = 
 , S Т =
, S Т = 
 . D = S Т AS =
. D = S Т AS =  .
.
В базисе B = (e 1, e 2, e 3) заданная квадратичная форма х А х имеет вид 9  – 9
– 9  + 18
+ 18  ,
,
а соответствующее преобразование координат:

2.5. Приведение кривой второго порядка к каноническому виду
Уравнение второго порядка вида  x 2 + 2
x 2 + 2 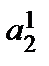 xy +
xy +  y 2 + 2
y 2 + 2  x + 2
x + 2  y +
y +  = 0 определяет на плоскости кривую. Группа членов B =
= 0 определяет на плоскости кривую. Группа членов B =  x 2 + 2
x 2 + 2 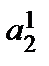 xy +
xy +  y 2называется квадратичной формой, L = 2
y 2называется квадратичной формой, L = 2  x + 2
x + 2  y – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.
y – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.
Матрица B =  называется матрицей квадратичной формы. Здесь
называется матрицей квадратичной формы. Здесь
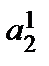 =
=  . Чтобы матрицу B привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда B =
. Чтобы матрицу B привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда B =  , где λ 1 и λ 2 – собственные числа матрицы B.
, где λ 1 и λ 2 – собственные числа матрицы B.
В базисе из собственных векторов матрицы B квадратичная форма будет иметь канонический вид:
λ 1  + λ 2
+ λ 2  .
.
Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.
Канонический вид кривой второго порядка: λ 1  + λ 2
+ λ 2  = a, причем:
= a, причем:
а) если λ 1 > 0, λ 2 > 0 – эллипс, в частности, при λ 1 = λ 2 это окружность;
б) если λ 1 > 0, λ 2 < 0 (λ 1 < 0, λ 2 > 0) имеем гиперболу;
в) если λ 1 = 0 либо λ 2 = 0, то кривая является параболой и после поворота осей координат
имеет вид λ 1  = ax 1 + by 1 + c (здесь λ 2 = 0). Дополняя до полного квадрата, будем
= ax 1 + by 1 + c (здесь λ 2 = 0). Дополняя до полного квадрата, будем
иметь: λ 1  = ax 1 + by 2.
= ax 1 + by 2.
Начало формы
Конец формы
Пример 1. Дано уравнение кривой 3 x 2 + 10 xy + 3 y 2 – 2 x – 14 y – 13 = 0
в системе координат (0, i, j), где i = {1, 0}, j = {0, 1}.
1). Определить тип кривой.
2). Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3). Найти соответствующие преобразования координат.
Р е ш е н и е. Приводим квадратичную форму B = 3 x 2 + 10 xy + 3 y 2к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы B =  . Находим собственные числа и собственные векторы этой матрицы:
. Находим собственные числа и собственные векторы этой матрицы:  .Характеристическое уравнение
.Характеристическое уравнение  = λ 2 − 6 λ −16 = 0 имеет корни: λ 1 = –2, λ 2 = 8.Вид квадратичнойформы: –2
= λ 2 − 6 λ −16 = 0 имеет корни: λ 1 = –2, λ 2 = 8.Вид квадратичнойформы: –2  + 8
+ 8 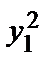 .Т.о., исходное уравнение определяет гиперболу.
.Т.о., исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать8  – 2
– 2  ,однако тип кривой остался тот же – гипербола.
,однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы B.
λ 1 = –2:  => x 1 + y 1 = 0.
=> x 1 + y 1 = 0.
Собственный вектор, отвечающий числу λ =–2при x 1=1: x 1= {1, –1}. В качестве единичного собственного вектора принимаем вектор i 1 =  ,где
,где 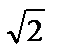 – длина вектора x 1.
– длина вектора x 1.
Координаты второго собственного вектора, соответствующего второму собственномучислу λ = 8,находим из системы  => x 1 –y 1 = 0 => x 2= {1, 1}, j 1 =
=> x 1 –y 1 = 0 => x 2= {1, 1}, j 1 = 
Итак, имеем новый ортонормированный базис(i 1, j 1).
По формулам x = S y переходим к новому базису:  =
= 
 или
или
x =  x 1 +
x 1 +  y 1, y = –
y 1, y = –  x 1 +
x 1 +  y 1. (*)
y 1. (*)
Вносим выражения x и y в исходное уравнение и, после преобразований, получаем:
–2  + 8
+ 8  +
+  x 1–
x 1–  y 1= 13
y 1= 13
Выделяем полные квадраты: –2  + 8
+ 8 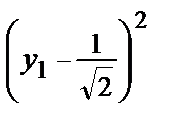 = 8.
= 8.
х 2= x 1–  , у 2= у 1–
, у 2= у 1–  .
.
Проводим параллельный перенос осей координат в новое начало: х 2= x 1–  , у 2= у 1–
, у 2= у 1–  .
.
Если внести эти соотношения в (*) и разрешить эти равенства относительно x 2и y 2, то получим:
х 2=  , у 2=
, у 2=  .
.
В системе координат(0*, i 1, j 1)данное уравнение имеет вид:– 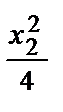 +
+  =1.
=1.
Для построения кривой строим в старой системе координат новую: ось x 2 = 0задается в старой системе координат уравнением x – y – 3 = 0,а ось y 2 = 0уравнением x + y – 1 = 0.Начало новой системы координат0 * (2, –1)является точкой пересечения этих прямых.
Для упрощения восприятия разобьем процесс построения графика на 2 этапа:
1. Переход к системе координат с осями x 2 = 0, y 2 = 0, заданными в старой системе координат уравнениями x – y – 3 = 0и x + y – 1= 0соответственно.
2. Построение в полученной системе координат графика функции.



Пример 2. Написать каноническое уравнение кривой второго порядка
9 х 2 – 4 ху + 6 у 2 + 16 х – 8 у – 2 = 0,
определить ее тип и найти каноническую систему координат.
Р е ш е н и е. Матрица квадратичной части многочлена второй степени равна  .
.
Ее собственные числа
(9 – λ) (6 – λ) – 4 = 0 => λ 2 – 15 λ + 50 = 0 => λ 1 = 5, λ 2 = 10;
собственные векторы:
λ 1 = 5:  => е 1 =
=> е 1 =  . λ 2 = 10:
. λ 2 = 10:  => е 2 =
=> е 2 =  .
.
Выполняя преобразования
х =  (х´ – 2 у´), у =
(х´ – 2 у´), у =  (2 х´ + у´),
(2 х´ + у´),
получаем
5 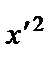 + 10
+ 10  –
–  у ´ – 2 = 0.
у ´ – 2 = 0.
Т.к. λ 1и λ 2отличны от нуля, то по каждой из новых переименованных х´ и у´ можно выделить полный квадрат:
по х´ полный квадрат уже есть (преобразование сдвига делать не нужно);
по у´: 10  –
–  у ´ = 10
у ´ = 10  – 8.
– 8.
Заменой переменных  = х ´,
= х ´,  = у ´–
= у ´–  , соответствующий сдвигу по оси Оу,получим
, соответствующий сдвигу по оси Оу,получим
5 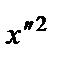 + 10
+ 10  – 10 = 0 или
– 10 = 0 или 
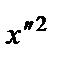 +
+  = 1.
= 1.
Данное уравнение есть каноническое уравнение эллипса. Результирующее преобразование координат имеет вид
х =  (
( – 2(
– 2( +
+  )) =
)) =  (
( – 2
– 2  ) –
) –  , у =
, у =  (2
(2  + (
+ ( +
+  )) х =
)) х =  (2
(2  +
+  ) +
) +  ,
,
а каноническая система координат(О´, е 1, е 2), где
О´ (–  ,
,  ), е 1 =
), е 1 = 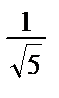 i +
i +  j, е 2 = –
j, е 2 = –  i +
i +  j.
j.
Задания. Написать каноническое уравнение кривой второго порядка определить ее тип и
найти каноническую систему координат:
1. 5  +6 x 1 x 2 – 3
+6 x 1 x 2 – 3  = 36.
= 36.
2. 4 x 1 x 2+3  = 16.
= 16.
3. 3  +2 x 1 x 2+3
+2 x 1 x 2+3  = 4.
= 4.
4. 4  +4 x 1 x 2+
+4 x 1 x 2+  = 20.
= 20.
5. 5  +12 x 1 x 2= 36.
+12 x 1 x 2= 36.
6.  – 6 x 1 x 2+
– 6 x 1 x 2+  = 8.
= 8.



 + 5
+ 5  + 2
+ 2  + 16 x 1 x 2 + 4 x 1 x 3–20 x 2 x 3
+ 16 x 1 x 2 + 4 x 1 x 3–20 x 2 x 3 .
. = (11− λ) (5− λ) (2− λ) + 2⋅8⋅(−10) + 2⋅8⋅(−10) − 2⋅(5− λ)⋅2−(11− λ)·
= (11− λ) (5− λ) (2− λ) + 2⋅8⋅(−10) + 2⋅8⋅(−10) − 2⋅(5− λ)⋅2−(11− λ)· =>
=>
 ~
~ 

 ~
~ 
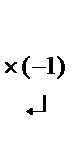 ~
~ 
 ~
~ 

 x 3.
x 3. .
. =
=  => e 1 =
=> e 1 =  .
.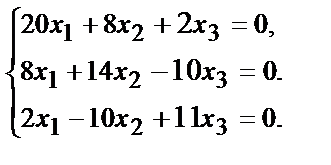

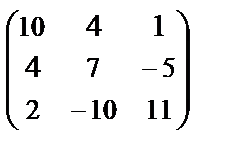

 ~
~ 
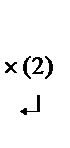
 ~
~ 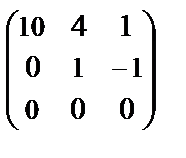
 Решая данную систему, получим x 1 = –
Решая данную систему, получим x 1 = –  .
. =
=  .
.


 ~
~ 

 ~
~ 
 ~
~ 
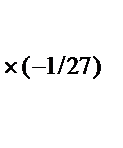 ~
~ =>
=> 
 .
. = 3 => e 3 =
= 3 => e 3 =  .
.
 , S Т =
, S Т =  . D = S Т AS =
. D = S Т AS =  .
. – 9
– 9  + 18
+ 18  ,
,
 x 2 + 2
x 2 + 2 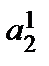 xy +
xy +  y 2 + 2
y 2 + 2  x + 2
x + 2  y +
y +  = 0 определяет на плоскости кривую. Группа членов B =
= 0 определяет на плоскости кривую. Группа членов B =  называется матрицей квадратичной формы. Здесь
называется матрицей квадратичной формы. Здесь . Чтобы матрицу B привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда B =
. Чтобы матрицу B привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда B =  , где λ 1 и λ 2 – собственные числа матрицы B.
, где λ 1 и λ 2 – собственные числа матрицы B. + λ 2
+ λ 2  .
. + λ 2
+ λ 2  = a, причем:
= a, причем: = ax 1 + by 2.
= ax 1 + by 2. . Находим собственные числа и собственные векторы этой матрицы:
. Находим собственные числа и собственные векторы этой матрицы:  .Характеристическое уравнение
.Характеристическое уравнение  = λ 2 − 6 λ −16 = 0 имеет корни: λ 1 = –2, λ 2 = 8.Вид квадратичнойформы: –2
= λ 2 − 6 λ −16 = 0 имеет корни: λ 1 = –2, λ 2 = 8.Вид квадратичнойформы: –2  + 8
+ 8 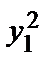 .Т.о., исходное уравнение определяет гиперболу.
.Т.о., исходное уравнение определяет гиперболу. – 2
– 2  ,однако тип кривой остался тот же – гипербола.
,однако тип кривой остался тот же – гипербола. => x 1 + y 1 = 0.
=> x 1 + y 1 = 0. ,где
,где 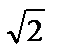 – длина вектора x 1.
– длина вектора x 1.  => x 1 –y 1 = 0 => x 2= {1, 1}, j 1 =
=> x 1 –y 1 = 0 => x 2= {1, 1}, j 1 = 
 =
= 
 или
или x 1 +
x 1 +  x 1–
x 1–  y 1= 13
y 1= 13 + 8
+ 8 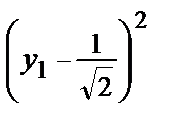 = 8.
= 8. , у 2= у 1–
, у 2= у 1–  .
. .
. , у 2=
, у 2=  .
.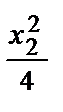 +
+  =1.
=1. 


 .
. => е 1 =
=> е 1 =  . λ 2 = 10:
. λ 2 = 10:  => е 2 =
=> е 2 =  .
. (х´ – 2 у´), у =
(х´ – 2 у´), у = 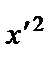 + 10
+ 10  –
–  у ´ – 2 = 0.
у ´ – 2 = 0. – 8.
– 8. = х ´,
= х ´,  = у ´–
= у ´–  , соответствующий сдвигу по оси Оу,получим
, соответствующий сдвигу по оси Оу,получим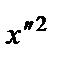 + 10
+ 10  – 10 = 0 или
– 10 = 0 или 
 – 2(
– 2( +
+  )) =
)) =  , у =
, у =  (2
(2  ,
, ), е 1 =
), е 1 = 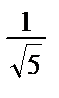 i +
i +  j, е 2 = –
j, е 2 = –  i +
i +  j.
j. = 36.
= 36. = 16.
= 16.


