СИСТЕМА ВЕКТОРОВ
1.1. Разложение вектора по системе векторов
Вектор k 1 a 1 + k 2 a 2 + … + kn a n называется линейной комбинацией векторов
a 1, a 2, …, a n скоэффициентами k 1, k 2, …, kn.
Вектор bлинейно выражается через векторы a 1, a 2, …, a n,если
b = k 1 a 1 + k 2 a 2 + … + kn a n.
В этом случае говорят также, что bразлагается по векторам a 1, a 2, …, a n. Каждый
n -мерный вектор b = { b 1, b 2, …, bn } однозначно разлагается по диагональной системе
e 1 = {1, 0, …, 0},
e 2 = {0, 1, …, 0},
..............
e n = {0, 0, …, 1}
с коэффициентами, которые равны координатам вектора b:
b = b 1 e 1 + b 2 e 2 + … + bn e n.
Чтобы найти разложение вектора b по системе векторов a 1, a 2, …, a n достаточно найти какое-нибудь решение системы уравнений
a 1 x 1 + a 2 x 2 + … + a nxn = b.
Пример.
Выяснить, разлагается ли вектор b по системе векторов a 1, a 2, …, a n:
b = { 2, 7, 17, 0}, a 1 = { 2, 4, 3, 0}, a 2 = { –3, 0, 1, 3}, a 3 = { 1, –1, 10, –3}.
Р е ш е н и е. Ищем общее решение системы уравнений
a 1 x 1 + a 2 x 2 + a 3 x 3= b
методомГаусса. Для этого запишем эту систему по координатам:

Расширенная матрица системы


 ~
~ 

 ~
~ 


~ 
 ~
~ 
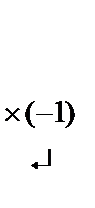 ~
~  .
.
Разрешенная система имеет вид:  (rA = rA|B = 3, n = 3).
(rA = rA|B = 3, n = 3).
Система определена: х 3 = 1, х 2 = 1, х 1 = 2.
Следовательно, b = 2 a 1+ a 2+ a 3.
Задания. Выяснить, разлагается ли вектор b по системе векторов a 1, a 2, …, a n:
1. b = { 2, 2, 3, 3}, a 1 = { 1, 2, 3, 1}, a 2 = { 2, 1, 2, 3}, a 3 = { 3, 2, 4, 4}.
2. b = { 4, 1, 3, 1}, a 1 = { 2, 0, 1, 1}, a 2 = { 1, 1, 2, -2}, a 3 = { 2, 1, 3, -3 }.
3. b = { -1, 1, 3, 1}, a 1 = { 1, 2, 1, 1}, a 2 = { 1, 1, 1, 2}, a 3 = { -3, -2, 1, -3}.
4. b = { 1, 0, 0, 1}, a 1 = { 2, 1, 1, 3}, a 2 = { 3, 0, -1, 2}, a 3 = { 1, -1, 0,1},
a 4 = { 1, 0, -2, -1 }.
5. Показать, что ни один из векторов диагональной системы не разлагается по остальным ее векторам.
6. Вектор b разлагается по системе векторов a 1, a 2, …, a m. Доказать, что каждый вектор системы b + a 1, b + a 2, …, b + a m разлагается по системе a 1, a 2, …, a m.
1.2. Линейная зависимость
Система векторов a 1, a 2, …, a n называется линейно зависимой, если можно подобрать такие числа k 1, k 2, …, kn, не все равные нулю, что
k 1 a 1 + k 2 a 2 + … + kn a n = Θ, где Θ = {0, 0, …, 0}.
Система векторов a 1, a 2, …, a n называется линейно независимой, если из каждого соотношения вида k 1 a 1 + k 2 a 2 + … + kn a n = Θ следует
k 1= k 2= … = kn =0.
Система векторов линейно зависима тогда и только тогда, когда система уравнений
a 1 x 1 + a 2 x 2 + … + a nxn = Θ
имеет ненулевое решение. Система векторов линейно н е зависима тогда и только тогда, когда система уравнений a 1 x 1 + a 2 x 2 + … + a nxn = Θ имеет только нулевое решение.
Вектор b разлагается по линейно независимой системе a 1, a 2, …, a n тогда и только тогда, когда a 1, a 2, …, a n, b – линейно зависимая система векторов.
Система векторов линейно зависима, если количество координат у векторов системы меньше, чем векторов в системе.
Если каждый вектор системы b 1, b 2, …, b n разлагается по векторам a 1, a 2, …, a m и n > m, то b 1, b 2, …, b n – линейно зависимая система векторов.
Пример 1.
Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
a 1 = { 3, 5, 1, 4}, a 2 = { –2, 1, -5, -7}, a 3 = { -1, –2, 0, –1}.
Р е ш е н и е. Ищем общее решение системы уравнений
a 1 x 1 + a 2 x 2 + a 3 x 3= Θ
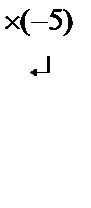
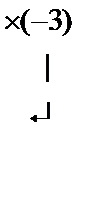
методомГаусса. Для этого запишем эту однородную систему по координатам:

Матрица системы

 ~
~ 
 ~
~ 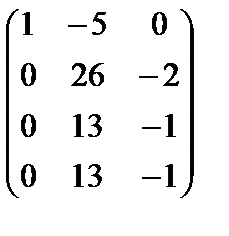

 ~
~ 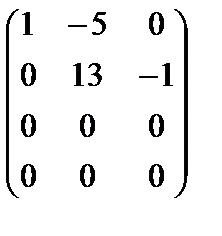 .
.
Разрешенная система имеет вид:  (rA = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2– свободная переменная): x 3 = 13 x 2; x 1=5 x 2 =>
(rA = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2– свободная переменная): x 3 = 13 x 2; x 1=5 x 2 =>
=> X o =  .Наличие ненулевого частного решения, например,
.Наличие ненулевого частного решения, например,  , говорит о том, векторы a 1, a 2, a 3 линейно зависимы.
, говорит о том, векторы a 1, a 2, a 3 линейно зависимы.
Пример 2.
Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
1. a 1 = { -20,-15, -4}, a 2 = { –7, -2, -4}, a 3 = { 3, –1, –2}.
Р е ш е н и е. Рассмотрим однородную систему уравнений a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
или в развернутом виде (по координатам)

Система однородна. Если она невырождена, то она имеет единственное решение. В случае однородной системы – нулевое (тривиальное) решение. Значит, в этом случае система векторов независима. Если же система вырождена, то она имеет ненулевые решения и, следовательно, она зависима.
Проверяем систему на вырожденность:
 = –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
Система невырождена и,т.о., векторы a 1, a 2, a 3 линейно независимы.
Задания. Выяснить,является ли данная система векторов линейно зависимой или линейно независимой:
1. a 1 = { -4, 2, 8}, a 2 = { 14, -7, -28}.
2. a 1 = { 2, -1, 3, 5}, a 2 = { 6, -3, 3, 15}.
3. a 1 = { -7, 5, 19}, a 2 = { -5, 7, -7}, a 3 = { -8, 7, 14}.
4. a 1 = { 1, 8, -1}, a 2 = { -2, 3, 3}, a 3 = { 4, -11, 9}.
5. a 1 = {0, 1, 1, 0}, a 2 = {1, 1, 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.
6. Доказать, что система векторов будет линейно зависимой, если она содержит:
а) два равных вектора;
б) два пропорциональных вектора.
7. Ненулевой вектор b разлагается по системе a 1, a 2, a 3 и по системе a 4, a 5, a 6. Доказать,
что a 1, a 2, a 3, a 4, a 5, a 6 линейно зависимая система векторов.
8. Доказать, что векторы a 2- a 1, a 3- a 1 не пропорциональны, если a 1, a 2, a 3– линейно
независимые векторы.
Пример.
Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:
а 1={5, 2, -3, 1}, а 2={4, 1, -2, 3}, а 3={1, 1, -1, -2}, а 4={3, 4, -1, 2}, а 5={13, 8, -7, 4}.
Р е ш е н и е. Рассмотрим однородную систему линейных уравнений
а 1 х 1 + а 2 х 2 + а 3 х 3 + а 4 х 4 + а 5 х 5= 0
или в развернутом виде  .
.
Будем решать эту систему методом Гаусса, не меняя местами строки и столбцы, и, кроме того, выбирая главный элемент не в верхнем левом углу, а по всей строке.Задача состоит в том, чтобы выделить диагональную часть преобразованной системы векторов.



 ~
~ 

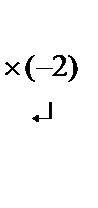
 ~
~
~ 
 ~
~ 


 ~
~  .
.
Разрешенная система векторов, равносильная исходной, имеет вид
а 11 х 1 + а 21 х 2 + а 31 х 3 + а 41 х 4 + а 51 х 5= 0,
где а 11=  , а 21=
, а 21=  , а 31=
, а 31=  , а 41=
, а 41= 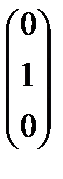 , а 51=
, а 51=  . (1)
. (1)
Векторы а 11, а 31, а 41образуют диагональную систему. Следовательно, векторы а 1, а 3, а 4 образуют базис системы векторов а 1, а 2, а 3, а 4, а 5.
Разложим теперь векторы а 2и а 5 по базису а 1, а 3, а 4. Для этого сначала разложим соответствующие векторы а 21и а 51 по диагональной системе а 11, а 31, а 41, имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты xi.
Из (1) имеем:
а 21= а 31· (-1) + а 41· 0 + а 11·1 => а 21= а 11 – а 31.
а 51= а 31· 0 + а 41· 1 + а 11·2 => а 51= 2 а 11 + а 41.
Векторы а 2и а 5 разлагаются по базису а 1, а 3, а 4 с теми же коэффициентами, что и векторы а 21и а 51 по диагональной системе а 11, а 31, а 41 (те коэффициенты xi). Следовательно,
а 2= а 1 – а 3, а 5= 2 а 1 + а 4.
Задания. 1. Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:
1. a 1 = { 1, 2, 1}, a 2 = { 2, 1, 3}, a 3 = { 1, 5, 0 }, a 4 = { 2, -2, 4}.
2. a 1 = { 1, 1, 2}, a 2 = { 0, 1, 2}, a 3 = { 2, 1, -4 }, a 4 = { 1, 1, 0}.
3. a 1 = { 1, -2, 3}, a 2 = { 0,1, -1}, a 3 = { 1, 3, 0}, a 4 = { 0, -7, 3 }, a 5 = { 1, 1, 1}.
4. a 1 = { 1, 2, -2}, a 2 = { 0, -1, 4}, a 3 = { 2, -3,3 }.
2. Найти все базисы системы векторов:
1. a 1 = { 1, 1, 2}, a 2 = { 3, 1, 2}, a 3 = { 1, 2, 1 }, a 4 = { 2, 1, 2}.
2. a 1 = { 1, 1, 1}, a 2 = { -3, -5, 5}, a 3 = { 3, 4, -1 }, a 4 = { 1, -1, 4}.
Пример.
Применяя процесс ортогонализации, построить ортогональную систему векторов:
а 1={2, 0, 1, 1}, а 2={1, 2, 0, 1}, а 3={0, 1, -2, 0}.
Р е ш е н и е. Полагаем b 1 = a 1. Затем строим векторы b 2 и b 3.
b 2 = a 2 –  b 1 = {1, 2, 0, 1} –
b 1 = {1, 2, 0, 1} –  ·{2, 0, 1, 1} = {1, 2, 0, 1} –
·{2, 0, 1, 1} = {1, 2, 0, 1} –  ·{2, 0, 1, 1} =
·{2, 0, 1, 1} =
= {0, 2, –  ,
,  };
};
b 3 = a 3 –  b 1–
b 1–  b 2 = {0, 1, -2, 0} –
b 2 = {0, 1, -2, 0} –  ·{2, 0, 1, 1}–
·{2, 0, 1, 1}–
–  ·{0, 2, –
·{0, 2, –  ,
,  }= {0, 1, -2, 0} – (–
}= {0, 1, -2, 0} – (–  ) ·{2, 0, 1, 1}–
) ·{2, 0, 1, 1}–  ·{0, 2, –
·{0, 2, –  ,
,  }=
}=
= {0, 1, -2, 0} +{  , 0,
, 0,  ,
,  }–{0,
}–{0,  , –
, –  ,
,  }={
}={  , –
, –  , –
, –  , 0}.
, 0}.
Т.о., векторы b 1 = {2, 0, 1, 1}, b 2 = {0, 2, –  ,
,  }, b 3 = {
}, b 3 = {  , –
, –  , –
, –  , 0} являются результатом ортогонализации исходной системы векторов.
, 0} являются результатом ортогонализации исходной системы векторов.
Задания. 1. Применяя процесс ортогонализации, построить ортогональную систему векторов:
1. {0, 1, 1}, {1, 1, 1}, {-3, 3, 1}.
2. {1, -1, 1}, {2, 1, 2}, {3, 1, 1}.
3. {1, -2, 1}, {0, 1, -4}, {2, -3, -2}, {7, 4, 1}.
4. {-1, 1, 1, 1}, {0, 2, 1, 1}, {1, 1, 1, 3}.
2. Преобразовать систему векторов
{1, -1, 1, 1}, {-1, 1, 1, 1}, {1, 1, 1, -1} в ортонормированную.
СИСТЕМА ВЕКТОРОВ
1.1. Разложение вектора по системе векторов
Вектор k 1 a 1 + k 2 a 2 + … + kn a n называется линейной комбинацией векторов
a 1, a 2, …, a n скоэффициентами k 1, k 2, …, kn.
Вектор bлинейно выражается через векторы a 1, a 2, …, a n,если
b = k 1 a 1 + k 2 a 2 + … + kn a n.
В этом случае говорят также, что bразлагается по векторам a 1, a 2, …, a n. Каждый
n -мерный вектор b = { b 1, b 2, …, bn } однозначно разлагается по диагональной системе
e 1 = {1, 0, …, 0},
e 2 = {0, 1, …, 0},
..............
e n = {0, 0, …, 1}
с коэффициентами, которые равны координатам вектора b:
b = b 1 e 1 + b 2 e 2 + … + bn e n.
Чтобы найти разложение вектора b по системе векторов a 1, a 2, …, a n достаточно найти какое-нибудь решение системы уравнений
a 1 x 1 + a 2 x 2 + … + a nxn = b.
Пример.
Выяснить, разлагается ли вектор b по системе векторов a 1, a 2, …, a n:
b = { 2, 7, 17, 0}, a 1 = { 2, 4, 3, 0}, a 2 = { –3, 0, 1, 3}, a 3 = { 1, –1, 10, –3}.
Р е ш е н и е. Ищем общее решение системы уравнений
a 1 x 1 + a 2 x 2 + a 3 x 3= b
методомГаусса. Для этого запишем эту систему по координатам:

Расширенная матрица системы


 ~
~ 

 ~
~ 


~ 
 ~
~ 
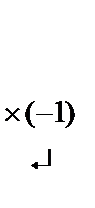 ~
~  .
.
Разрешенная система имеет вид:  (rA = rA|B = 3, n = 3).
(rA = rA|B = 3, n = 3).
Система определена: х 3 = 1, х 2 = 1, х 1 = 2.
Следовательно, b = 2 a 1+ a 2+ a 3.
Задания. Выяснить, разлагается ли вектор b по системе векторов a 1, a 2, …, a n:
1. b = { 2, 2, 3, 3}, a 1 = { 1, 2, 3, 1}, a 2 = { 2, 1, 2, 3}, a 3 = { 3, 2, 4, 4}.
2. b = { 4, 1, 3, 1}, a 1 = { 2, 0, 1, 1}, a 2 = { 1, 1, 2, -2}, a 3 = { 2, 1, 3, -3 }.
3. b = { -1, 1, 3, 1}, a 1 = { 1, 2, 1, 1}, a 2 = { 1, 1, 1, 2}, a 3 = { -3, -2, 1, -3}.
4. b = { 1, 0, 0, 1}, a 1 = { 2, 1, 1, 3}, a 2 = { 3, 0, -1, 2}, a 3 = { 1, -1, 0,1},
a 4 = { 1, 0, -2, -1 }.
5. Показать, что ни один из векторов диагональной системы не разлагается по остальным ее векторам.
6. Вектор b разлагается по системе векторов a 1, a 2, …, a m. Доказать, что каждый вектор системы b + a 1, b + a 2, …, b + a m разлагается по системе a 1, a 2, …, a m.
1.2. Линейная зависимость
Система векторов a 1, a 2, …, a n называется линейно зависимой, если можно подобрать такие числа k 1, k 2, …, kn, не все равные нулю, что
k 1 a 1 + k 2 a 2 + … + kn a n = Θ, где Θ = {0, 0, …, 0}.
Система векторов a 1, a 2, …, a n называется линейно независимой, если из каждого соотношения вида k 1 a 1 + k 2 a 2 + … + kn a n = Θ следует
k 1= k 2= … = kn =0.
Система векторов линейно зависима тогда и только тогда, когда система уравнений
a 1 x 1 + a 2 x 2 + … + a nxn = Θ
имеет ненулевое решение. Система векторов линейно н е зависима тогда и только тогда, когда система уравнений a 1 x 1 + a 2 x 2 + … + a nxn = Θ имеет только нулевое решение.
Вектор b разлагается по линейно независимой системе a 1, a 2, …, a n тогда и только тогда, когда a 1, a 2, …, a n, b – линейно зависимая система векторов.
Система векторов линейно зависима, если количество координат у векторов системы меньше, чем векторов в системе.
Если каждый вектор системы b 1, b 2, …, b n разлагается по векторам a 1, a 2, …, a m и n > m, то b 1, b 2, …, b n – линейно зависимая система векторов.
Пример 1.
Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
a 1 = { 3, 5, 1, 4}, a 2 = { –2, 1, -5, -7}, a 3 = { -1, –2, 0, –1}.
Р е ш е н и е. Ищем общее решение системы уравнений
a 1 x 1 + a 2 x 2 + a 3 x 3= Θ
методомГаусса. Для этого запишем эту однородную систему по координатам:

Матрица системы

 ~
~ 


 ~
~ 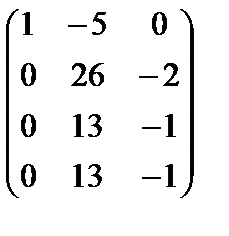

 ~
~  .
.
Разрешенная система имеет вид:  (rA = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2– свободная переменная): x 3 = 13 x 2; x 1=5 x 2 =>
(rA = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2– свободная переменная): x 3 = 13 x 2; x 1=5 x 2 =>
=> X o =  .Наличие ненулевого частного решения, например,
.Наличие ненулевого частного решения, например,  , говорит о том, векторы a 1, a 2, a 3 линейно зависимы.
, говорит о том, векторы a 1, a 2, a 3 линейно зависимы.
Пример 2.
Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
1. a 1 = { -20,-15, -4}, a 2 = { –7, -2, -4}, a 3 = { 3, –1, –2}.
Р е ш е н и е. Рассмотрим однородную систему уравнений a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
или в развернутом виде (по координатам)

Система однородна. Если она невырождена, то она имеет единственное решение. В случае однородной системы – нулевое (тривиальное) решение. Значит, в этом случае система векторов независима. Если же система вырождена, то она имеет ненулевые решения и, следовательно, она зависима.
Проверяем систему на вырожденность:
 = –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
Система невырождена и,т.о., векторы a 1, a 2, a 3 линейно независимы.
Задания. Выяснить,является ли данная система векторов линейно зависимой или линейно независимой:
1. a 1 = { -4, 2, 8}, a 2 = { 14, -7, -28}.
2. a 1 = { 2, -1, 3, 5}, a 2 = { 6, -3, 3, 15}.
3. a 1 = { -7, 5, 19}, a 2 = { -5, 7, -7}, a 3 = { -8, 7, 14}.
4. a 1 = { 1, 8, -1}, a 2 = { -2, 3, 3}, a 3 = { 4, -11, 9}.
5. a 1 = {0, 1, 1, 0}, a 2 = {1, 1, 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.
6. Доказать, что система векторов будет линейно зависимой, если она содержит:
а) два равных вектора;
б) два пропорциональных вектора.
7. Ненулевой вектор b разлагается по системе a 1, a 2, a 3 и по системе a 4, a 5, a 6. Доказать,
что a 1, a 2, a 3, a 4, a 5, a 6 линейно зависимая система векторов.
8. Доказать, что векторы a 2- a 1, a 3- a 1 не пропорциональны, если a 1, a 2, a 3– линейно
независимые векторы.
Базис и ранг системы векторов
Часть системы векторов называется базисом этой системы, если:
1) эта часть является линейно независимой системой векторов;
2) каждый вектор системы разлагается по векторам этой части.
Диагональная система векторов является базисом каждой системы, которая содержит ее в качестве части.
Если система уравнений
a 1 x 1 + a 2 x 2 + … + a nxn = Θ
является разрешенной, то векторы-коэффициенты при неизвестных, составляющих набор разрешенных неизвестных, образуют диагональную часть системы векторов a 1, a 2, …, a n.
Векторы системы разлагаются по базису этой системы е д и н с т в е н н ы м образом.
Каждую линейно независимую часть системы векторов можно дополнить до базиса этой системы.
Все базисы данной системы состоят из одного и того же числа векторов.
Рангом системы векторов называется число векторов в любом ее базисе. Если ранг системы векторов равен r, то каждая линейно независимая часть этой системы, состоящая из r векторов, является ее базисом. Системы векторов называются эквивалентными, если векторы одной системы разлагаются по векторам другой системы и наоборот. Ранги эквивалентных систем равны.
Вектор b тогда и только тогда разлагается по системе векторов a 1, a 2, …, a m, когда ранги систем a 1, a 2, …, a m и a 1, a 2, …, a m, b равны.
Построение базиса системы векторов a 1, a 2, …, an и разложений векторов по базису:
1) Рассмотреть систему уравнений a 1 x 1 + a 2 x 2 + … + a nxn = Θ и найти равносильную ей разрешенную систему уравнений
a´ 1 x 1 + a´ 2 x 2 + … + a´ nxn = Θ.
2) Найти диагональную часть системы векторов a´ 1, a´ 2, …, a´ n.
3) Отметить векторы системы a 1, a 2, …, a n, соответствующие диагональной части системы a´ 1, a´ 2, …, a´ n;они образуют базис системы a 1, a 2, …, a n.
4) Разложить вектор a´ j по диагональной части системы a´ 1, a´ 2, …, a´ n; вектор a j, 1 ≤ j ≤ n, разлагается по базису, найденному в пункте 3, с коэффициентами разложения a´ j по диагональной части системы a´ 1, a´ 2, …, a´ n.
Пример.
Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:
а 1={5, 2, -3, 1}, а 2={4, 1, -2, 3}, а 3={1, 1, -1, -2}, а 4={3, 4, -1, 2}, а 5={13, 8, -7, 4}.
Р е ш е н и е. Рассмотрим однородную систему линейных уравнений
а 1 х 1 + а 2 х 2 + а 3 х 3 + а 4 х 4 + а 5 х 5= 0
или в развернутом виде  .
.
Будем решать эту систему методом Гаусса, не меняя местами строки и столбцы, и, кроме того, выбирая главный элемент не в верхнем левом углу, а по всей строке.Задача состоит в том, чтобы выделить диагональную часть преобразованной системы векторов.



 ~
~ 

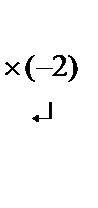
 ~
~
~ 
 ~
~ 


 ~
~  .
.
Разрешенная система векторов, равносильная исходной, имеет вид
а 11 х 1 + а 21 х 2 + а 31 х 3 + а 41 х 4 + а 51 х 5= 0,
где а 11=  , а 21=
, а 21=  , а 31=
, а 31=  , а 41=
, а 41= 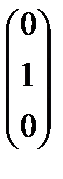 , а 51=
, а 51=  . (1)
. (1)
Векторы а 11, а 31, а 41образуют диагональную систему. Следовательно, векторы а 1, а 3, а 4 образуют базис системы векторов а 1, а 2, а 3, а 4, а 5.
Разложим теперь векторы а 2и а 5 по базису а 1, а 3, а 4. Для этого сначала разложим соответствующие векторы а 21и а 51 по диагональной системе а 11, а 31, а 41, имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты xi.
Из (1) имеем:
а 21= а 31· (-1) + а 41· 0 + а 11·1 => а 21= а 11 – а 31.
а 51= а 31· 0 + а 41· 1 + а 11·2 => а 51= 2 а 11 + а 41.
Векторы а 2и а 5 разлагаются по базису а 1, а 3, а 4 с теми же коэффициентами, что и векторы а 21и а 51 по диагональной системе а 11, а 31, а 41 (те коэффициенты xi). Следовательно,
а 2= а 1 – а 3, а 5= 2 а 1 + а 4.
Задания. 1. Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:
1. a 1 = { 1, 2, 1}, a 2 = { 2, 1, 3}, a 3 = { 1, 5, 0 }, a 4 = { 2, -2, 4}.
2. a 1 = { 1, 1, 2}, a 2 = { 0, 1, 2}, a 3 = { 2, 1, -4 }, a 4 = { 1, 1, 0}.
3. a 1 = { 1, -2, 3}, a 2 = { 0,1, -1}, a 3 = {






 ~
~ 

 ~
~ 



 ~
~ 
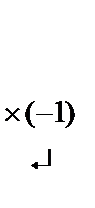 ~
~  .
. (rA = rA|B = 3, n = 3).
(rA = rA|B = 3, n = 3).

 ~
~ 


 ~
~ 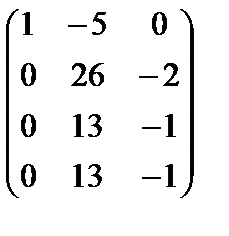

 ~
~  .
. (rA = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2– свободная переменная): x 3 = 13 x 2; x 1=5 x 2 =>
(rA = 2, n = 3). Система совместна и неопределена. Ее общее решение (x 2– свободная переменная): x 3 = 13 x 2; x 1=5 x 2 => .Наличие ненулевого частного решения, например,
.Наличие ненулевого частного решения, например,  , говорит о том, векторы a 1, a 2, a 3 линейно зависимы.
, говорит о том, векторы a 1, a 2, a 3 линейно зависимы.
 = –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0. .
.


 ~
~ 

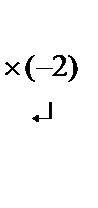
 ~
~
 ~
~ 


 ~
~  .
. , а 21=
, а 21=  , а 31=
, а 31=  , а 41=
, а 41= 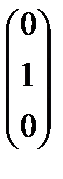 , а 51=
, а 51=  . (1)
. (1) b 1 = {1, 2, 0, 1} –
b 1 = {1, 2, 0, 1} –  ·{2, 0, 1, 1} = {1, 2, 0, 1} –
·{2, 0, 1, 1} = {1, 2, 0, 1} –  ·{2, 0, 1, 1} =
·{2, 0, 1, 1} = b 1–
b 1–  b 2 = {0, 1, -2, 0} –
b 2 = {0, 1, -2, 0} –  ·{2, 0, 1, 1}–
·{2, 0, 1, 1}– ·{0, 2, –
·{0, 2, –  ) ·{2, 0, 1, 1}–
) ·{2, 0, 1, 1}–  ·{0, 2, –
·{0, 2, –  , –
, – 


