Деревом называется связный граф, не имеющий циклов. В графе без циклов, таким образом, каждая компонента связности является деревом. Такой граф называют лесом.
Рассмотрим некоторые свойства деревьев. Отметим сначала, что в дереве всякий путь – простой, так как в пути, не являющимся простым, обязательно содержится цикл.
Лемма 5. В дереве для любых двух вершин существует единственный соединяющий их простой путь.
Доказательство. Существование пути следует из связности дерева. Допустим, что в некотором дереве существуют два различных простых пути, соединяющих вершины a и b. Начальные отрезки этих путей совпадают (оба пути начинаются в одной и той же вершине a). Пусть x – последняя вершина этого совпадающего начала, а после x в одном пути следует вершина 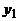 , а в другом –
, а в другом –  . Рассмотрим ребро
. Рассмотрим ребро  . Если его удалить из графа, то в оставшемся подграфе вершины
. Если его удалить из графа, то в оставшемся подграфе вершины 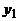 и x будут соединимыми – соединяющий их маршрут можно построить так: взять отрезок первого пути от
и x будут соединимыми – соединяющий их маршрут можно построить так: взять отрезок первого пути от 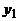 до a и к нему присоединить отрезок второго от x до a, взятый в обратном порядке. Но это означает, что ребро
до a и к нему присоединить отрезок второго от x до a, взятый в обратном порядке. Но это означает, что ребро  не является перешейком. Однако из леммы 4 следует, что в дереве каждое ребро является перешейком.
не является перешейком. Однако из леммы 4 следует, что в дереве каждое ребро является перешейком.
Из леммы 5 следует, что во всяком дереве, в котором не меньше двух вершин, имеется вершина степени 1. Такие вершины называют висячими вершинами, или листьями. В действительности легко доказать, что в каждом дереве не меньше двух листьев, а цепь 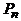 – пример дерева, в котором точно два листа.
– пример дерева, в котором точно два листа.
Теорема 5. В любом дереве с n вершинами имеется ровно  ребро.
ребро.
Доказательство. Индукция по числу вершин. При  утверждение очевидно. При
утверждение очевидно. При  в дереве имеется хотя бы один лист. Если из дерева удалить лист, то снова получится дерево, так как циклов не появится, а связность сохранится. В этом новом дереве
в дереве имеется хотя бы один лист. Если из дерева удалить лист, то снова получится дерево, так как циклов не появится, а связность сохранится. В этом новом дереве 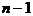 вершина и, по предположению индукции,
вершина и, по предположению индукции,  ребра. Следовательно, в исходном дереве было
ребра. Следовательно, в исходном дереве было 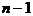 ребро.
ребро.
Если к дереву добавить новое ребро, то, поскольку вершины, соединяемые этим ребром, уже были соединены путем, образуется цикл. Таким образом, деревья – это графы, экстремальные по обоим свойствам из их определения: с одной стороны, это минимальные связные графы (при удалении любого ребра нарушается связность), с другой – максимальные графы без циклов (при добавлении любого нового ребра появляется цикл).
Центр дерева
Центр графа может состоять из одной вершины (как, например, в графе 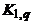 ), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.
), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.
Лемма 6. В дереве для каждой вершины a имеется не более одной смежной с ней вершины b такой, что 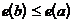 .
.
Доказательство. Пусть x – вершина, наиболее удаленная от a, то есть 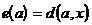 . Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно,
. Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно, 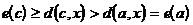 .
.
Теорема 6. Центр дерева состоит из одной вершины или двух смежных вершин.
Доказательство. Допустим, что в некотором дереве существуют две несмежные центральные вершины a и b. Рассмотрим путь, соединяющий эти вершины, и найдем на этом пути промежуточную вершину x с максимальным эксцентриситетом. Так как a и b – вершины с наименьшим эксцентриситетом в дереве, то эксцентриситет x также не меньше эксцентриситета этих вершин. Но тогда оказывается, что 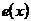 не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин.
не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин.
Двудольные графы
Граф называется двудольным, если множество его вершин можно так разбить на два подмножества, чтобы концы каждого ребра принадлежали разным подмножествам. Эти подмножества называются долями. Таким образом, каждая из долей порождает пустой подграф. Примером двудольного графа является простая цепь 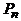 при любом n: одна доля порождается вершинами с четными номерами, другая – с нечетными. Граф
при любом n: одна доля порождается вершинами с четными номерами, другая – с нечетными. Граф 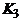 – пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.
– пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.
Теорема 7 (теорема Кенига). Следующие утверждения для графа G равносильны:
(1) G – двудольный граф;
(2) в G нет циклов нечетной длины;
(3) в G нет простых циклов нечетной длины.
Доказательство. (1)Þ(2). Пусть G – двудольный граф, в котором выбрано некоторое разбиение на доли, 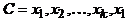 – цикл длины k в графе G. При любом
– цикл длины k в графе G. При любом 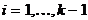 вершины
вершины 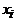 и
и 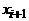 смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е.
смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е. 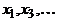 , другая – из всех вершин с четными индексами. Но вершины
, другая – из всех вершин с четными индексами. Но вершины 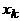 и
и 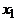 тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.
тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.
Импликация (2)Þ(3) очевидна, докажем (3)Þ(1). Рассмотрим граф G, в котором нет простых циклов нечетной длины. Ясно, что граф, в котором каждая компонента связности – двудольный граф, сам двудольный. Поэтому можно считать, что граф G связен. Зафиксируем в нем некоторую вершину a и докажем, что для любых двух смежных между собой вершин x и y имеет место равенство 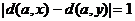 . Действительно, допустим, что
. Действительно, допустим, что 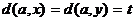 . Пусть
. Пусть 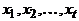 – кратчайший путь из a в x,
– кратчайший путь из a в x, 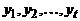 – кратчайший путь из a в y. Эти пути начинаются в одной вершине:
– кратчайший путь из a в y. Эти пути начинаются в одной вершине: 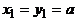 , а оканчиваются в разных:
, а оканчиваются в разных: 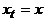 ,
, 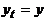 . Поэтому найдется такое k, что
. Поэтому найдется такое k, что 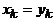 и
и 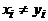 при всех
при всех 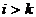 . Но тогда последовательность
. Но тогда последовательность 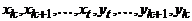 является простым циклом длины
является простым циклом длины 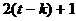 . Следовательно,
. Следовательно, 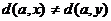 . Предположим, что
. Предположим, что 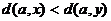 . Если
. Если 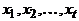 – кратчайший путь из a в x, то, очевидно,
– кратчайший путь из a в x, то, очевидно, 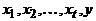 – кратчайший путь из a в y, следовательно,
– кратчайший путь из a в y, следовательно, 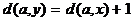 . Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех вершин с нечетными расстояниями до a, то для каждого ребра графа один из его концов принадлежит множеству A, другой – множеству B. Следовательно, граф G –двудольный.
. Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех вершин с нечетными расстояниями до a, то для каждого ребра графа один из его концов принадлежит множеству A, другой – множеству B. Следовательно, граф G –двудольный.
Пусть C – цикл в графе G. Множество вершин цикла C порождает в G подграф, который содержит все ребра этого цикла, но может содержать и ребра, ему не принадлежащие. Такие ребра называют хордами цикла C. Простой цикл, не имеющий хорд, – это порожденный подграф, изоморфный простому циклу, будем его коротко называть порожденным простым циклом. В графе, изображенном на рисунке 12, хордами цикла 4,1,2,6,5,4 являются ребра (1,5), (1,6) и (2,5), а цикл 2,3,7,6,2 – порожденный простой цикл. Заметим, что любой цикл длины 3 является порожденным простым циклом.

Рис. 12
Пусть C – простой цикл длины k в некотором графе, (x, y) – хорда этого цикла. Ребро (x, y) вместе с ребрами цикла C образует два цикла меньшей длины,  и
и  (см. рисунок 13), сумма длин которых равна
(см. рисунок 13), сумма длин которых равна  .
.

Рис. 13.
Значит, если C – цикл нечетной длины, то один из циклов  ,
,  тоже имеет нечетную длину. Отсюда следует, что в графе, в котором есть цикл нечетной длины, имеется и порожденный простой цикл нечетной длины. Поэтому критерий двудольности справедлив и в следующей формулировке.
тоже имеет нечетную длину. Отсюда следует, что в графе, в котором есть цикл нечетной длины, имеется и порожденный простой цикл нечетной длины. Поэтому критерий двудольности справедлив и в следующей формулировке.
Следствие. Граф является двудольным тогда и только тогда, когда в нем нет порожденных простых циклов нечетной длины.
Планарные графы
Геометрический граф – это плоская фигура, состоящая из вершин – точек плоскости и ребер – линий, соединяющих некоторые пары вершин. Всякий граф можно многими способами представить геометрическим графом и мы уже не раз пользовались этой возможностью. На рисунке 14 показаны два геометрических графа  и
и  , представляющих, как нетрудно проверить, один и тот же обыкновенный граф. Простое устройство этого графа, очевидное на левом изображении, не так легко обнаружить, рассматривая правое.
, представляющих, как нетрудно проверить, один и тот же обыкновенный граф. Простое устройство этого графа, очевидное на левом изображении, не так легко обнаружить, рассматривая правое.




Рис. 14
Главная причина этого – в том, что в  ребра не имеют «лишних» пересечений. Геометрический граф, в котором никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины, называют плоским графом, а по отношению к представляемому им обыкновенному графу – его плоской укладкой. Не каждый граф допускает плоскую укладку. Граф, для которого существует плоская укладка, называется планарным графом. Кроме удобства визуального анализа, есть немало поводов, в том числе и сугубо практических, для интереса к планарным графам и их плоским укладкам.
ребра не имеют «лишних» пересечений. Геометрический граф, в котором никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины, называют плоским графом, а по отношению к представляемому им обыкновенному графу – его плоской укладкой. Не каждый граф допускает плоскую укладку. Граф, для которого существует плоская укладка, называется планарным графом. Кроме удобства визуального анализа, есть немало поводов, в том числе и сугубо практических, для интереса к планарным графам и их плоским укладкам.
Если плоскость разрезать по ребрам плоского графа, она распадется на связные части, которые называют гранями. Всегда имеется одна неограниченная внешняя грань, все остальные грани называются внутренними. Если в плоском

Рис. 15
графе нет циклов, то у него имеется только одна грань. Если же циклы есть, то граница каждой грани содержит цикл, но не обязательно является циклом. На рисунке 15 показан плоский граф с пятью занумерованными гранями. Граница грани с номером 3 состоит из двух циклов, а граница грани с номером 2 кроме цикла длины 5 включает еще дерево из трех ребер. Множества ребер, образующие границы граней, могут быть разными для разных плоских укладок одного и того же графа. На рисунке 16 показаны две плоские укладки одного графа. В левой есть две грани, границы которых являются простыми циклами длины 5, в правой же таких нет, но есть грани, ограниченные циклами длины 4
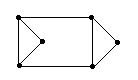

Рис. 16
и 6. Однако число граней, как показывает следующая теорема, не зависит от укладки, т.е. является инвариантом планарного графа.
Теорема 8 (формула Эйлера). Количество граней в любой плоской укладке планарного графа, имеющего n вершин, m ребер и k компонент связности, равно  .
.
Доказательство. Докажем сначала утверждение теоремы при 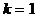 . Рассмотрим связный плоский граф G. Если в нем нет циклов, то имеется единственная грань, а
. Рассмотрим связный плоский граф G. Если в нем нет циклов, то имеется единственная грань, а  , и формула верна. Если же есть хотя бы один цикл, то возьмем какое-нибудь ребро e, принадлежащее простому циклу C. Это ребро принадлежит границе двух граней, одна из которых целиком лежит внутри цикла C, другая – снаружи. Если удалить ребро e из графа, эти две грани сольются в одну. Граф
, и формула верна. Если же есть хотя бы один цикл, то возьмем какое-нибудь ребро e, принадлежащее простому циклу C. Это ребро принадлежит границе двух граней, одна из которых целиком лежит внутри цикла C, другая – снаружи. Если удалить ребро e из графа, эти две грани сольются в одну. Граф  , полученный из графа G удалением ребра e, очевидно, будет плоским и связным, в нем на одно ребро и на одну грань меньше, чем в G, а число вершин осталось прежним. Если в
, полученный из графа G удалением ребра e, очевидно, будет плоским и связным, в нем на одно ребро и на одну грань меньше, чем в G, а число вершин осталось прежним. Если в  еще есть циклы, то, удалив еще одно цикловое ребро, получим граф
еще есть циклы, то, удалив еще одно цикловое ребро, получим граф 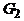 . Будем продолжать удаление цикловых ребер до тех пор, пока не получится связный плоский граф
. Будем продолжать удаление цикловых ребер до тех пор, пока не получится связный плоский граф  без циклов, т.е. дерево. У него
без циклов, т.е. дерево. У него  ребро и единственная грань. Значит, всего было удалено
ребро и единственная грань. Значит, всего было удалено  ребер, а так как при удалении каждого ребра число граней уменьшалось на единицу, то в исходном графе было
ребер, а так как при удалении каждого ребра число граней уменьшалось на единицу, то в исходном графе было  грани. Таким образом, формула верна для любого связного плоского графа. Если граф не связен, то в компоненте связности, имеющей
грани. Таким образом, формула верна для любого связного плоского графа. Если граф не связен, то в компоненте связности, имеющей  вершин и
вершин и  ребер, по доказанному, будет
ребер, по доказанному, будет  внутренняя грань. Суммируя по всем компонентам и прибавляя 1 для учета внешней грани, убеждаемся в справедливости формулы в общем случае.
внутренняя грань. Суммируя по всем компонентам и прибавляя 1 для учета внешней грани, убеждаемся в справедливости формулы в общем случае.
Следствие 1. Если в планарном графе n вершин,  , и m ребер, то
, и m ребер, то  .
.
Доказательство. Если в графе нет циклов, то  и неравенство выполняется при
и неравенство выполняется при  . Рассмотрим плоский граф G с r гранями, в котором имеются циклы. Занумеруем грани числами от 1 до r и обозначим через
. Рассмотрим плоский граф G с r гранями, в котором имеются циклы. Занумеруем грани числами от 1 до r и обозначим через  количество ребер, принадлежащих грани с номером i. Так как граница каждой грани содержит цикл, то
количество ребер, принадлежащих грани с номером i. Так как граница каждой грани содержит цикл, то  для каждого i, следовательно,
для каждого i, следовательно,  . С другой стороны, каждое ребро принадлежит границе не более чем двух граней, поэтому
. С другой стороны, каждое ребро принадлежит границе не более чем двух граней, поэтому  . Из этих двух неравенств следует, что
. Из этих двух неравенств следует, что  . Применяя формулу Эйлера, получаем
. Применяя формулу Эйлера, получаем  .
.
Следствие 1 дает необходимое условие планарности, которое в некоторых случаях позволяет установить, что граф не является планарным. Рассмотрим, например, полный граф  . У него
. У него  ,
,  и мы видим, что неравенство из следствия 1 не выполняется. Значит, этот граф не планарен. В то же время существуют графы, не являющиеся планарными, для которых неравенство следствия 1 выполняется. Пример – полный двудольный граф
и мы видим, что неравенство из следствия 1 не выполняется. Значит, этот граф не планарен. В то же время существуют графы, не являющиеся планарными, для которых неравенство следствия 1 выполняется. Пример – полный двудольный граф  . У него 6 вершин и 9 ребер. Неравенство выполняется, но мы сейчас установим, что он не планарен. Заметим, что в этом графе нет циклов длины 3 (так как он двудольный, в нем вообще нет циклов нечетной длины). Поэтому граница каждой грани содержит не менее четырех ребер. Повторяя рассуждения из доказательства следствия 1, но используя неравенство
. У него 6 вершин и 9 ребер. Неравенство выполняется, но мы сейчас установим, что он не планарен. Заметим, что в этом графе нет циклов длины 3 (так как он двудольный, в нем вообще нет циклов нечетной длины). Поэтому граница каждой грани содержит не менее четырех ребер. Повторяя рассуждения из доказательства следствия 1, но используя неравенство  вместо
вместо  , получаем следующий результат.
, получаем следующий результат.
Следствие 2. Если в планарном графе n вершин,  , m ребер и нет циклов длины 3, то
, m ребер и нет циклов длины 3, то  .
.
Для графа  неравенство следствия 2 не выполняется, это доказывает, что он не планарен.
неравенство следствия 2 не выполняется, это доказывает, что он не планарен.
Известно несколько критериев планарности, сформулируем без доказательства один из них. Операция подразбиения ребра  состоит в выполнении следующих действий:
состоит в выполнении следующих действий:
· ребро  удаляется из графа;
удаляется из графа;
· добавляется новая вершина с;
· добавляются ребра  и
и  .
.
Два графа называют гомеоморфными, если из них с помощью подразбиения ребер можно получить изоморфные графы. На рисунке 17 изображены гомеоморфные графы.


Рис.17
Теорема 9 (теорема Понтрягина–Куратовского). Граф планарен тогда и только тогда, когда у него нет подграфов, гомеоморфных  или
или  .
.



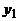 , а в другом –
, а в другом –  . Рассмотрим ребро
. Рассмотрим ребро  . Если его удалить из графа, то в оставшемся подграфе вершины
. Если его удалить из графа, то в оставшемся подграфе вершины 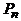 – пример дерева, в котором точно два листа.
– пример дерева, в котором точно два листа. ребро.
ребро. утверждение очевидно. При
утверждение очевидно. При  в дереве имеется хотя бы один лист. Если из дерева удалить лист, то снова получится дерево, так как циклов не появится, а связность сохранится. В этом новом дереве
в дереве имеется хотя бы один лист. Если из дерева удалить лист, то снова получится дерево, так как циклов не появится, а связность сохранится. В этом новом дереве 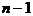 вершина и, по предположению индукции,
вершина и, по предположению индукции,  ребра. Следовательно, в исходном дереве было
ребра. Следовательно, в исходном дереве было 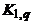 ), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.
), а может включать все его вершины (полный граф). Для дерева, как мы увидим, имеется гораздо более ограниченный диапазон возможностей.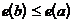 .
.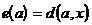 . Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно,
. Единственный путь из a в x проходит через одну из вершин, смежных с a, пусть это вершина b. Если c – другая вершина, смежная с a, то единственный путь из c в x проходит через b и его длина на единицу больше длины пути из a в x. Следовательно, 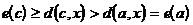 .
. 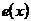 не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин.
не меньше эксцентриситетов двух смежных с ней вершин – предшествующей ей и следующей за ней на пути, а это противоречит лемме 6. Следовательно, любые две центральные вершины смежны, а так как в дереве не может быть трех попарно смежных вершин, то в нем не больше двух центральных вершин. 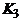 – пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.
– пример графа, не являющегося двудольным: при любом разбиении множества его вершин на два подмножества в одном из этих подмножеств окажутся две смежных вершины.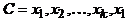 – цикл длины k в графе G. При любом
– цикл длины k в графе G. При любом 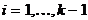 вершины
вершины 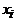 и
и 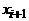 смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е.
смежны и, следовательно, принадлежат разным долям. Таким образом, одна доля состоит из всех вершин с нечетными индексами, т.е. 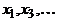 , другая – из всех вершин с четными индексами. Но вершины
, другая – из всех вершин с четными индексами. Но вершины 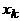 и
и 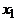 тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.
тоже смежны и должны принадлежать разным долям. Следовательно, k – четное число.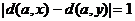 . Действительно, допустим, что
. Действительно, допустим, что 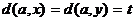 . Пусть
. Пусть 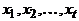 – кратчайший путь из a в x,
– кратчайший путь из a в x, 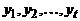 – кратчайший путь из a в y. Эти пути начинаются в одной вершине:
– кратчайший путь из a в y. Эти пути начинаются в одной вершине: 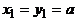 , а оканчиваются в разных:
, а оканчиваются в разных: 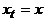 ,
, 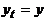 . Поэтому найдется такое k, что
. Поэтому найдется такое k, что 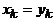 и
и 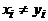 при всех
при всех 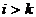 . Но тогда последовательность
. Но тогда последовательность 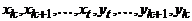 является простым циклом длины
является простым циклом длины 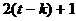 . Следовательно,
. Следовательно, 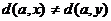 . Предположим, что
. Предположим, что 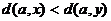 . Если
. Если 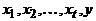 – кратчайший путь из a в y, следовательно,
– кратчайший путь из a в y, следовательно, 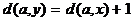 . Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех вершин с нечетными расстояниями до a, то для каждого ребра графа один из его концов принадлежит множеству A, другой – множеству B. Следовательно, граф G –двудольный.
. Итак, расстояния от двух смежных вершин до вершины a различаются ровно не единицу. Поэтому, если обозначить через A множество всех вершин графа, расстояние от которых до вершины a четно, а через B множество всех вершин с нечетными расстояниями до a, то для каждого ребра графа один из его концов принадлежит множеству A, другой – множеству B. Следовательно, граф G –двудольный. 
 и
и  (см. рисунок 13), сумма длин которых равна
(см. рисунок 13), сумма длин которых равна  .
.
 и
и  , представляющих, как нетрудно проверить, один и тот же обыкновенный граф. Простое устройство этого графа, очевидное на левом изображении, не так легко обнаружить, рассматривая правое.
, представляющих, как нетрудно проверить, один и тот же обыкновенный граф. Простое устройство этого графа, очевидное на левом изображении, не так легко обнаружить, рассматривая правое.




 .
. . Рассмотрим связный плоский граф G. Если в нем нет циклов, то имеется единственная грань, а
. Рассмотрим связный плоский граф G. Если в нем нет циклов, то имеется единственная грань, а  , и формула верна. Если же есть хотя бы один цикл, то возьмем какое-нибудь ребро e, принадлежащее простому циклу C. Это ребро принадлежит границе двух граней, одна из которых целиком лежит внутри цикла C, другая – снаружи. Если удалить ребро e из графа, эти две грани сольются в одну. Граф
, и формула верна. Если же есть хотя бы один цикл, то возьмем какое-нибудь ребро e, принадлежащее простому циклу C. Это ребро принадлежит границе двух граней, одна из которых целиком лежит внутри цикла C, другая – снаружи. Если удалить ребро e из графа, эти две грани сольются в одну. Граф  , полученный из графа G удалением ребра e, очевидно, будет плоским и связным, в нем на одно ребро и на одну грань меньше, чем в G, а число вершин осталось прежним. Если в
, полученный из графа G удалением ребра e, очевидно, будет плоским и связным, в нем на одно ребро и на одну грань меньше, чем в G, а число вершин осталось прежним. Если в 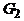 . Будем продолжать удаление цикловых ребер до тех пор, пока не получится связный плоский граф
. Будем продолжать удаление цикловых ребер до тех пор, пока не получится связный плоский граф  без циклов, т.е. дерево. У него
без циклов, т.е. дерево. У него  ребро и единственная грань. Значит, всего было удалено
ребро и единственная грань. Значит, всего было удалено  ребер, а так как при удалении каждого ребра число граней уменьшалось на единицу, то в исходном графе было
ребер, а так как при удалении каждого ребра число граней уменьшалось на единицу, то в исходном графе было  грани. Таким образом, формула верна для любого связного плоского графа. Если граф не связен, то в компоненте связности, имеющей
грани. Таким образом, формула верна для любого связного плоского графа. Если граф не связен, то в компоненте связности, имеющей  вершин и
вершин и  ребер, по доказанному, будет
ребер, по доказанному, будет  внутренняя грань. Суммируя по всем компонентам и прибавляя 1 для учета внешней грани, убеждаемся в справедливости формулы в общем случае.
внутренняя грань. Суммируя по всем компонентам и прибавляя 1 для учета внешней грани, убеждаемся в справедливости формулы в общем случае.  , и m ребер, то
, и m ребер, то  .
. и неравенство выполняется при
и неравенство выполняется при  количество ребер, принадлежащих грани с номером i. Так как граница каждой грани содержит цикл, то
количество ребер, принадлежащих грани с номером i. Так как граница каждой грани содержит цикл, то  для каждого i, следовательно,
для каждого i, следовательно,  . С другой стороны, каждое ребро принадлежит границе не более чем двух граней, поэтому
. С другой стороны, каждое ребро принадлежит границе не более чем двух граней, поэтому  . Из этих двух неравенств следует, что
. Из этих двух неравенств следует, что  . Применяя формулу Эйлера, получаем
. Применяя формулу Эйлера, получаем  .
.  . У него
. У него  ,
,  и мы видим, что неравенство из следствия 1 не выполняется. Значит, этот граф не планарен. В то же время существуют графы, не являющиеся планарными, для которых неравенство следствия 1 выполняется. Пример – полный двудольный граф
и мы видим, что неравенство из следствия 1 не выполняется. Значит, этот граф не планарен. В то же время существуют графы, не являющиеся планарными, для которых неравенство следствия 1 выполняется. Пример – полный двудольный граф  . У него 6 вершин и 9 ребер. Неравенство выполняется, но мы сейчас установим, что он не планарен. Заметим, что в этом графе нет циклов длины 3 (так как он двудольный, в нем вообще нет циклов нечетной длины). Поэтому граница каждой грани содержит не менее четырех ребер. Повторяя рассуждения из доказательства следствия 1, но используя неравенство
. У него 6 вершин и 9 ребер. Неравенство выполняется, но мы сейчас установим, что он не планарен. Заметим, что в этом графе нет циклов длины 3 (так как он двудольный, в нем вообще нет циклов нечетной длины). Поэтому граница каждой грани содержит не менее четырех ребер. Повторяя рассуждения из доказательства следствия 1, но используя неравенство  вместо
вместо  .
. состоит в выполнении следующих действий:
состоит в выполнении следующих действий: и
и  .
.


