Маршруты, пути, циклы
Маршрут в графе – это последовательность вершин 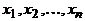 , такая, что для каждого
, такая, что для каждого 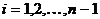 вершины
вершины 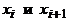 соединены ребром. Эти
соединены ребром. Эти 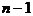 ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число
ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число 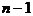 называют длиной маршрута. Говорят, что маршрут соединяет вершины
называют длиной маршрута. Говорят, что маршрут соединяет вершины  , они называются соответственно началом и концом маршрута, вершины
, они называются соответственно началом и концом маршрута, вершины 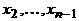 называются промежуточными. Маршрут называется замкнутым, если
называются промежуточными. Маршрут называется замкнутым, если 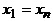 .
.
Путь – это маршрут, в котором все ребра различны. Путь называется простым, если и все вершины в нем различны.
Цикл – это замкнутый путь. Цикл 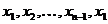 называется простым, если вершины
называется простым, если вершины 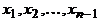 все попарно различны.
все попарно различны.
В графе на рисунке 9 последовательность вершин
2,3,5,4 – не маршрут;
2,3,4,5,1,4,3 – маршрут, но не путь;
3,1,4,5,1,2 – путь, но не простой;
2,3,1,4,3,1,2 – замкнутый маршрут, но не цикл;
2,3,1,4,5,1,2 – цикл, но не простой;
2,3,4,5,1,2 – простой цикл.
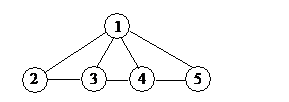
Рис. 9
Установим некоторые простые свойства путей и циклов.
Лемма 1. В любом маршруте, соединяющем две различные вершины, содержится простой путь, соединяющий те же вершины.
Доказательство. Пусть 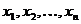 – маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть
– маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть 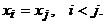 Тогда последовательность
Тогда последовательность 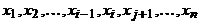 , полученная из этого маршрута удалением отрезка последовательности от
, полученная из этого маршрута удалением отрезка последовательности от 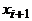 до
до 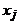 , тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий
, тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий  .
.

Лемма 2. Во всяком цикле, проходящем через некоторое ребро, содержится простой цикл, проходящий через это ребро.
Доказательство. Пусть имеется цикл, проходящий через ребро 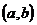 . Если удалить это ребро из графа, то в полученном подграфе останется маршрут, соединяющий a и b. По лемме 1.3 существует простой путь
. Если удалить это ребро из графа, то в полученном подграфе останется маршрут, соединяющий a и b. По лемме 1.3 существует простой путь 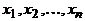 , соединяющий эти вершины, то есть пара
, соединяющий эти вершины, то есть пара 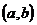 совпадает (как неупорядоченная пара) с парой
совпадает (как неупорядоченная пара) с парой 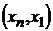 . Но тогда
. Но тогда 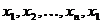 – простой цикл в исходном графе, проходящий через ребро
– простой цикл в исходном графе, проходящий через ребро 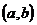 .
.
Отметим, что в формулировке леммы 2 нельзя заменить слово «цикл» словами «замкнутый маршрут». Действительно, если 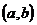 – ребро графа, то последовательность
– ребро графа, то последовательность 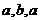 – замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.
– замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.
Лемма 3. Если в графе степень каждой вершины не меньше 2, то в нем есть цикл.
Доказательство. Найдем в графе простой путь наибольшей длины (он существует, так как длина простого пути не может превышать 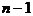 ). Пусть это
). Пусть это 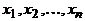 . Вершина
. Вершина 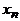 смежна с
смежна с 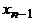 , а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность
, а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность 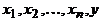 была бы простым путем большей длины. Следовательно, y – это одна из вершин пути,
была бы простым путем большей длины. Следовательно, y – это одна из вершин пути, 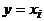 , причем
, причем 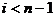 . Но тогда
. Но тогда 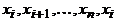 – цикл.
– цикл.
Связность и компоненты
Граф называется связным, если в нем для любых двух вершин имеется маршрут, соединяющий эти вершины. Заметим, что ввиду леммы 1 можно в этом определении заменить слово «маршрут» словами «простой путь».
Для произвольного графа определим на множестве вершин отношение соединимости: вершина a соединима с вершиной b, если существует соединяющий их маршрут. Легко видеть, что это отношение рефлексивно, симметрично и транзитивно, то есть является отношением эквивалентности. Классы эквивалентности называются областями связности, а порождаемые ими подграфы – компонентами связности графа. В связном графе имеется только одна компонента связности – весь граф. Компоненты связности можно определить также как максимальные по включению связные подграфы данного графа.
Ребро, при удалении которого увеличивается число компонент связности, называется перешейком.
Лемма 4. Ребро является перешейком в том и только том случае, если через него не проходит никакой цикл.
Доказательство. Если через ребро (a,b) проходит цикл, то после удаления этого ребра вершины a и b останутся соединимыми, значит, число компонент связности не увеличится. Обратно, если после удаления ребра (a,b) число компонент связности не увеличивается, то вершины a и b останутся в одной компоненте, то есть существует соединяющий их маршрут, не проходящий через это ребро. По лемме 1 в нем имеется простой путь x 1, x 2,…, xn, соединяющий a и b, но тогда x 1, x 2,…, xn, x 1– цикл, проходящий через (a,b).
Эйлеровы циклы
Первая теорема теории графов была доказана задолго до того, как стало употребляться словосочетание «теория графов». В 1736 г. появилась работа Эйлера, в которой не только была решена предложенная ему задача о кенигсбергских мостах, но и сформулировано общее правило, позволяющее решить любую задачу такого рода. Интересно, что в одном из писем Эйлер писал по этому поводу: «...это решение по своему характеру, по-видимому, имеет мало отношения к математике, и мне непонятно, почему следует скорее от математика ожидать этого решения, нежели от какого-нибудь другого человека...».
На языке теории графов задача состоит в том, чтобы определить, имеется ли в графе путь, проходящий через все его ребра (напомним, что путь, по определению, не может дважды проходить по одному ребру). Такой путь называется эйлеровым путем, а если он замкнут, то эйлеровым циклом. Граф, в котором есть эйлеров цикл, называют эйлеровым графом. В графе, изображенном на рисунке 10а, эйлеров цикл существует, – например, последовательность вершин 1,2,4,5,2,3,5,6,3,1 образует такой цикл. В графе же на рисунке 10б эйлерова цикла нет, но есть эйлеровы пути, например, 2,4,5,2,1,3,5,6,3.
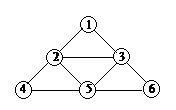
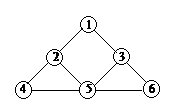
а б
Рис. 10
Рассмотрим сначала условия существования эйлерова цикла в обыкновенном графе. Ясно, что в несвязном графе эйлеров цикл может существовать только в том случае, когда все его ребра принадлежат одной компоненте связности, а все остальные компоненты – просто изолированные вершины. Поэтому достаточно рассматривать связные графы.
Теорема 3. С вязный граф эйлеров тогда и только тогда, когда в нем степени всех вершин четны.
Доказательство. Необходимость условия очевидна, так как при каждом прохождении цикла через какую-либо вершину используются два ребра – по одному из них маршрут входит в вершину, по другому выходит (это относится и к стартовой вершине – в нее ведь придется вернуться). Докажем его достаточность.
Пусть G – связный граф, в котором больше одной вершины и степени всех вершин четны. Значит, степень каждой вершины не меньше 2 и, по лемме 3, в графе G имеется цикл 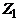 . Если удалить все ребра этого цикла из графа G, то получится граф
. Если удалить все ребра этого цикла из графа G, то получится граф  , в котором степени вершин также четны. Если в
, в котором степени вершин также четны. Если в  нет ни одного ребра, то
нет ни одного ребра, то 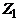 – эйлеров цикл. В противном случае, применяя ту же лемму 3 к графу, полученному из
– эйлеров цикл. В противном случае, применяя ту же лемму 3 к графу, полученному из  удалением всех изолированных вершин, заключаем, что в
удалением всех изолированных вершин, заключаем, что в  имеется цикл
имеется цикл 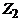 . Удалив из
. Удалив из  все ребра цикла
все ребра цикла 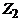 , получим граф
, получим граф 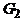 . Продолжая действовать таким образом, пока не придем к пустому графу, получим в итоге систему циклов
. Продолжая действовать таким образом, пока не придем к пустому графу, получим в итоге систему циклов 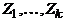 , причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов
, причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов 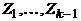 имеет общую вершину с
имеет общую вершину с  . Допустим, для определенности, что таков цикл
. Допустим, для определенности, что таков цикл 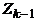 . Пусть
. Пусть 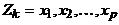 ,
, 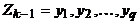 , и
, и 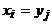 для некоторых i и j. Тогда последовательность вершин
для некоторых i и j. Тогда последовательность вершин
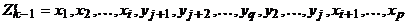
очевидно, является циклом, а множество ребер этого цикла есть объединение множеств ребер циклов 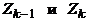 . Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым.
. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым.
Теперь нетрудно получить и критерий существования эйлерова пути.
Теорема 4. Эйлеров путь в связном графе существует тогда и только тогда, когда в нем имеется не более двух вершин с нечетными степенями.
Доказательство. Если в графе нет вершин с нечетными степенями, то, по предыдущей теореме, в нем имеется эйлеров цикл, он является и эйлеровым путем. Не может быть точно одной вершины с нечетной степенью – это следует из «леммы о рукопожатиях». Если же имеются точно две вершины с нечетными степенями, то построим новый граф, добавив ребро, соединяющее эти вершины. В новом графе степени всех вершин четны и, следовательно, существует эйлеров цикл. Так как циклический сдвиг цикла – тоже цикл, то существует и такой эйлеров цикл, в котором добавленное ребро – последнее. Удалив из этого цикла последнюю вершину, получим эйлеров путь в исходном графе.


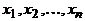 , такая, что для каждого
, такая, что для каждого 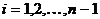 вершины
вершины 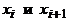 соединены ребром. Эти
соединены ребром. Эти 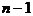 ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число
ребер называются ребрами маршрута, говорят, что маршрут проходит через них, а число  , они называются соответственно началом и концом маршрута, вершины
, они называются соответственно началом и концом маршрута, вершины 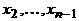 называются промежуточными. Маршрут называется замкнутым, если
называются промежуточными. Маршрут называется замкнутым, если 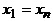 .
.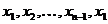 называется простым, если вершины
называется простым, если вершины 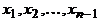 все попарно различны.
все попарно различны.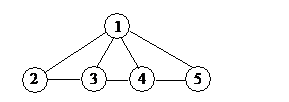
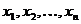 – маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть
– маршрут. Если все его вершины различны, то это уже простой путь. В противном случае, пусть 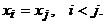 Тогда последовательность
Тогда последовательность 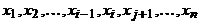 , полученная из этого маршрута удалением отрезка последовательности от
, полученная из этого маршрута удалением отрезка последовательности от 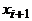 до
до 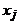 , тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий
, тоже является маршрутом. Новый маршрут соединяет те же вершины и имеет меньшую длину. Продолжая действовать таким образом, после конечного числа «спрямлений» получим простой путь, соединяющий 
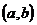 . Если удалить это ребро из графа, то в полученном подграфе останется маршрут, соединяющий a и b. По лемме 1.3 существует простой путь
. Если удалить это ребро из графа, то в полученном подграфе останется маршрут, соединяющий a и b. По лемме 1.3 существует простой путь 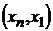 . Но тогда
. Но тогда 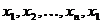 – простой цикл в исходном графе, проходящий через ребро
– простой цикл в исходном графе, проходящий через ребро 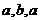 – замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.
– замкнутый маршрут, проходящий через это ребро, но никакого цикла в нем нет.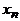 смежна с
смежна с 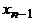 , а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность
, а так как ее степень не меньше двух, то она смежна еще хотя бы с одной вершиной, скажем, y. Если y была бы отлична от всех вершин пути, то последовательность 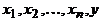 была бы простым путем большей длины. Следовательно, y – это одна из вершин пути,
была бы простым путем большей длины. Следовательно, y – это одна из вершин пути, 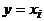 , причем
, причем 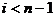 . Но тогда
. Но тогда 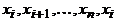 – цикл.
– цикл. 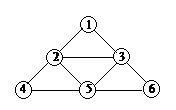
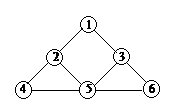
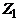 . Если удалить все ребра этого цикла из графа G, то получится граф
. Если удалить все ребра этого цикла из графа G, то получится граф  , в котором степени вершин также четны. Если в
, в котором степени вершин также четны. Если в 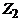 . Удалив из
. Удалив из 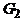 . Продолжая действовать таким образом, пока не придем к пустому графу, получим в итоге систему циклов
. Продолжая действовать таким образом, пока не придем к пустому графу, получим в итоге систему циклов 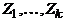 , причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов
, причем каждое ребро графа принадлежит в точности одному из них. Покажем теперь, что из этих циклов можно составить один цикл. Действительно, из того, что исходный граф связен, следует, что хотя бы один из циклов 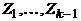 имеет общую вершину с
имеет общую вершину с  . Допустим, для определенности, что таков цикл
. Допустим, для определенности, что таков цикл 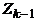 . Пусть
. Пусть 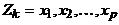 ,
, 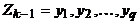 , и
, и 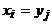 для некоторых i и j. Тогда последовательность вершин
для некоторых i и j. Тогда последовательность вершин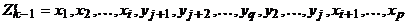
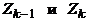 . Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым.
. Таким образом, получаем систему из меньшего числа циклов, по-прежнему обладающую тем свойством, что каждое ребро графа принадлежит в точности одному из них. Понятно, что продолжая действовать таким образом, в конце концов получим один цикл, который и будет эйлеровым.