1. Геометрический смысл производной

Пусть
y =
f (
x) определена в

и дифференцируема в некоторой внутренней точке

. Пусть M
0(
x 0;
y 0) - некоторая точка графика функции, а М(
х;
у)- некоторая другая точка. Прямая М
0М называется
секущей кривой
y =
f (
x). Если оставить точку М
0 неподвижной, а точку М перемещать по кривой в направлении к М
0, то секущая будет поворачиваться вокруг М
0. При М

М
0 она будет стремиться к некоторому предельному положению М
0Т.
Определение. Касательной к кривой называется предельное положение секущей М0М, когда М  М0 по кривой.
М0 по кривой.
D х = х-х 0 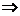

 .
.
Пусть секущая р, проходящая через точки М0(х 0; y 0) и М(х 0+D х; у 0+D y) образует с положительным направлением оси О х угол  . Из DМ0АМ
. Из DМ0АМ
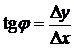
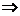
 , (1)
, (1)
т.е. j = j (D x). Если D х  0, то М
0, то М  М0 по графику функции, и D y
М0 по графику функции, и D y  0. Следовательно, секущая будет поворачиваться, и угол j будет изменяться. Так как arctg x - непрерывная функция то
0. Следовательно, секущая будет поворачиваться, и угол j будет изменяться. Так как arctg x - непрерывная функция то
 .
.
То есть существует  правой части (1). Значит, существует и
правой части (1). Значит, существует и  левой части, т.е. существует
левой части, т.е. существует  , и имеет место равенство
, и имеет место равенство  . Следовательно, существует предельное положение угла j, которое обозначим через j 0, т.е существует предельное положение М0Т секущей М0М при М
. Следовательно, существует предельное положение угла j, которое обозначим через j 0, т.е существует предельное положение М0Т секущей М0М при М  М0. Следовательно, М0Т- касательная к графику у = f (x) в точке М0 и
М0. Следовательно, М0Т- касательная к графику у = f (x) в точке М0 и
 Û
Û 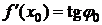 .
.
Геометрический смысл производной состоит в следующем: производная функции f (x) в точке х 0 равна угловому коэффициенту касательной к кривой y = f (x) в точке (х 0; f (x 0)) (равна тангенсу угла наклона касательной к положительному направлению оси О х)
Таким образом доказана
Теорема. Если функция f дифференцируема в точке х 0 (существует конечная производная 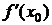 ), то график этой функции имеет касательную, угловой коэффициент которой равен
), то график этой функции имеет касательную, угловой коэффициент которой равен 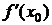 .
.
Замечание. 1) Если 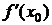 =0, то касательная к кривой в точке х 0 параллельна оси О х (tg
=0, то касательная к кривой в точке х 0 параллельна оси О х (tg  =0
=0 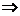
 =0).
=0).
2) Если 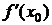 =¥
=¥  tg
tg  0=¥
0=¥ 
 , то касательная к графику перпендикулярна оси О х (функция не дифференцируема в точке х 0, а касательная существует).
, то касательная к графику перпендикулярна оси О х (функция не дифференцируема в точке х 0, а касательная существует).
 3) Может быть, что
3) Может быть, что 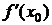 не существует, а касательная перпендикулярна оси О х.
не существует, а касательная перпендикулярна оси О х.
Пример. 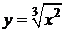 - не дифференцируема в точке х =0. Прямая х =0 (ось О y) – касательная к графику в точке х 0=0.
- не дифференцируема в точке х =0. Прямая х =0 (ось О y) – касательная к графику в точке х 0=0.
2. Геометрический смысл дифференциала
Из рисунка: из DМ0АВ 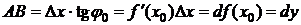 .
.
Геометрический смысл дифференциала: дифференциал функции y = f (x) в точке х 0- это приращение ординаты точки касательной к графику функции в точке M0(x 0; y 0), соответствующее приращению аргумента D х.
3. Уравнение касательной и нормали к графику функции y = f (x)
Известно, что всякая прямая не параллельная оси О у, проходящая через точку M0(x 0; y 0), имеет уравнение  .
.
 Пусть f (x) дифференцируема в точке х 0. Следовательно, график функции имеет в точке (x 0; y 0) касательную, угловой коэффициент которой
Пусть f (x) дифференцируема в точке х 0. Следовательно, график функции имеет в точке (x 0; y 0) касательную, угловой коэффициент которой 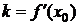 . Тогда уравнение касательной имеет вид
. Тогда уравнение касательной имеет вид
 .
.
Прямая, проходящая через точку M0(x 0; y 0) и перпендикулярная к касательной, называется нормалью к графику функции f в точке M0(x 0; y 0). Т.к. коэффициенты перпендикулярных прямых k 1 и k 2, связаны соотношением 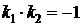 , то
, то  ,
,  , и, значит, уравнение нормали имеет вид
, и, значит, уравнение нормали имеет вид
 .
.




 и дифференцируема в некоторой внутренней точке
и дифференцируема в некоторой внутренней точке  . Пусть M0(x 0; y 0) - некоторая точка графика функции, а М(х; у)- некоторая другая точка. Прямая М0М называется секущей кривой y = f (x). Если оставить точку М0 неподвижной, а точку М перемещать по кривой в направлении к М0, то секущая будет поворачиваться вокруг М0. При М
. Пусть M0(x 0; y 0) - некоторая точка графика функции, а М(х; у)- некоторая другая точка. Прямая М0М называется секущей кривой y = f (x). Если оставить точку М0 неподвижной, а точку М перемещать по кривой в направлении к М0, то секущая будет поворачиваться вокруг М0. При М  М0 она будет стремиться к некоторому предельному положению М0Т.
М0 она будет стремиться к некоторому предельному положению М0Т.
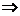

 .
. . Из DМ0АМ
. Из DМ0АМ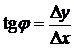
 , (1)
, (1) .
. правой части (1). Значит, существует и
правой части (1). Значит, существует и  , и имеет место равенство
, и имеет место равенство  . Следовательно, существует предельное положение угла j, которое обозначим через j 0, т.е существует предельное положение М0Т секущей М0М при М
. Следовательно, существует предельное положение угла j, которое обозначим через j 0, т.е существует предельное положение М0Т секущей М0М при М  Û
Û 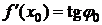 .
.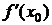 ), то график этой функции имеет касательную, угловой коэффициент которой равен
), то график этой функции имеет касательную, угловой коэффициент которой равен  =0
=0  tg
tg  , то касательная к графику перпендикулярна оси О х (функция не дифференцируема в точке х 0, а касательная существует).
, то касательная к графику перпендикулярна оси О х (функция не дифференцируема в точке х 0, а касательная существует). 3) Может быть, что
3) Может быть, что 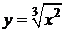 - не дифференцируема в точке х =0. Прямая х =0 (ось О y) – касательная к графику в точке х 0=0.
- не дифференцируема в точке х =0. Прямая х =0 (ось О y) – касательная к графику в точке х 0=0. 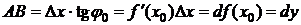 .
. .
. Пусть f (x) дифференцируема в точке х 0. Следовательно, график функции имеет в точке (x 0; y 0) касательную, угловой коэффициент которой
Пусть f (x) дифференцируема в точке х 0. Следовательно, график функции имеет в точке (x 0; y 0) касательную, угловой коэффициент которой 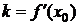 . Тогда уравнение касательной имеет вид
. Тогда уравнение касательной имеет вид .
.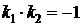 , то
, то  ,
,  , и, значит, уравнение нормали имеет вид
, и, значит, уравнение нормали имеет вид .
.


