КЛАССИЧЕСКАЯ РЕГРЕССИЯ
Цель: привитие умения и навыков построения экспериментально-статистической модели объекта с использованием процедур регрессионного анализа.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
Основные положения регрессионного анализа.
Исследуется некоторый объект, между выходной характеристикой которого и входными "объясняющими", иначе предикторными, переменными существует функциональная связь. Из-за влияния различных неучтенных факторов и помех (в том числе ошибок измерения), проявляющихся вкупе как случайные возмущения, зависимость между выходом и входом будет не функциональная, а стохастическая. В регрессионном анализе ищут зависимость между математическим ожиданием выходной величины, которое обозначают как y,от выходных переменных, которые полагаются неслучайными.
Искомая функция специфицируется как линейная комбинация выбираемых из априорных соображений базисных функций от объясняющих переменных x 1, x 2,…, xn:
y =a 0 f 0(x 1 ,…,xn) + a 1 f 1(x 1 ,…,xn) + ….+ak fk (x1,…,xn),
где a 0, a 1,…, ak – параметры, иначе коэффициенты регрессии;
f 0(…), f 1(…),…, fk (…) – базисные функции.
Обычно f 0(…) тождественно равна единице, соответствующий коэффициент a 0 называют свободным членом.
Для оценивания параметров над исследуемым объектом проводят N >(k +1) наблюдений, в ходе которых фиксируются значения выходной и входных переменных:
Оценку â параметров находят по методу наименьших квадратов, обеспечивающему минимум остаточной суммы квадратов:
где ŷi - значение выходной переменной в i -й точке наблюдения, предсказанное по уравнению регрессии.
Оценка â коэффициентов регрессии a вычисляется как:
где F - матрица значений базисных функций, т.е.
Статистический анализ полученных соотношений возможен при введении дополнительной информации, а именно: случайное возмущение u аддитивно, распределено по нормальному закону, имеет нулевое математическое ожидание, постоянную дисперсию s2 для всей области допустимых значений переменных x 1, x 2, …, xn, а значения возмущений в любых двух несовпадающих точках некоррелированы.
С учетом сказанного отдельное наблюдение ỹ 1 можно представить в виде
Для проверки адекватности полученного уравнения регрессии
ŷ = a 0 ƒ 0 (x 1 ,…,xn) + a 1 ƒ 1 (x 1 ,…,xn) + … + akƒk(x1,…,xn)
сопоставляют две оценки дисперсии случайного возмущения. Первая из них S 2
вычисляется как
и характеризует достигнутую точность оцененной модели, а вторая – S 2В есть дисперсия воспроизводимости, определяемая по результатам m наблюдений в одной и той же точке области изменения переменных. Строят F -отношение F р = S2/S2 В и сравнивают его с табличным F т при заданном уровне надежности (обычно 0,95) с числом степеней свободы числителя N -(k +1) и знаменателя m -1. Если F р > F т, то гипотеза об адекватности отвергается.
В случае, если оценку воспроизводимости получить не представляется возможным, а следовательно, нельзя проверить и адекватность, то прибегают к косвенным измерителям качества регрессии. Широкое применение получил коэффициент детерминации
R 2:
Числитель в выражении для R 2 есть объясненная с помощью уравнения регрессии сумма квадратов отклонений выходной переменной от ее среднего значения, а знаменатель - сумма квадратов отклонений наблюденных значений от среднего.
Чем ближе R 2 к единице, тем меньше расхождения между наблюденными и оцененными значениями выходной переменной, и в этом смысле R 2 можно рассматривать как меру согласия модели с данными.
Заметим, что наряду с (3.3) используется более точная, несмещенная, оценка истинного значения коэффициента детерминации, так называемый правленый коэффициент детерминации
Для проверки гипотезы, что все коэффициенты регрессии, кроме соответствующего свободному члену a 0, равны нулю, сравнивают
с табличным значением
F т при заданном уровне надежности и числом степеней свободы числителя
k и знаменателя
N -(
k +1); при
F р >
F т гипотеза отвергается.
В программных системах по статистике, значение F р приводится либо в последнем столбце таблицы дисперсионного анализа (Analysis of Variance), либо сразу после нее. Объясненная с помощью регрессии сумма квадратов связывается с источником изменчивости, называемым моделью.
Полезным средством при построении регрессионной модели является исследование остатков ûi = ỹi –ŷi, i = 1,2,…, N. Наличие выбросов, серий положительных или отрицательных знаков в ряде остатков могут свидетельствовать о неадекватности модели. Вообще-то говоря, между реализацией случайного возмущения u и его оценкой û (u и N -мерные векторы) существует линейная связь:
где I -единичная матрица.
Наличие связи приводит к коррелированности оцененных остатков, затрудняя тем самым проверку некоррелированности реализаций случайного возмущения. Это затруднение можно обойти с помощью статистики d Дарбина - Уотсона, определяемой как:
Статистики d затабулированы. Таблица для определенного уровня значимости (обычно 0,05) является двухвходовой: строки соответствуют числу наблюдений, столбцы- числу членов уравнения регрессии, не считая свободного. В каждом столбце приводится два значения d L и dU. Если d, рассчитанное по (3.5), окажется меньше d L, гипотеза о некоррелированности истинных остатков отвергается, если d больше d U -принимается. При d L £ d £ d U имеет место неопределенность.
Для проверки значимости отдельного коэффициента регрессии â i строят отношение
t р = | âi |/ ciis 2 ,
где сii - диагональный элемент матрицы (F'F)-1, соответствующий i -му коэффициенту. t р сравнивают с табличным t т значением t -статистики при выбранном уровне значимости и числе степеней свободы, равном N -(k +1). При t р < t т гипотеза H 0: ai =0 принимается, в противном случае отвергается.
Незначимые коэффициенты должны быть исключены из уравнения регрессии, а остальные коэффициенты пересчитаны.
В задачах пассивного эксперимента, когда исследователь, собирая данные, не может влиять на значения объясняющих переменных, возможно явление мультиколлинеарности. Это явление имеет место, когда между столбцами матрицы F значений базисных функций существует почти точная линейная зависимость. В этом случае оценки коэффициентов регрессии определяются не сколько зависимостью между выходом и входом, сколько возможными возмущениями объясняющих переменных.
Универсальной меры мультиколлинеарности не существует. На практике используются следующие:
а) минимальное собственное значение (СЗ) lmin матрицы F'F;
б) отношение максимального СЗ матрицы F'F к минимальному СЗ lmax/lmin;
в) максимальное абсолютное значение элементов матрицы сопряженности (корреляции) базисных функций r max
Мультиколлинеарность тем больше, чем меньше lmin , больше lmax/lmin, чем ближе r max к единице.
Одним из методов получения оценок коэффициентов регрессии при наличии мультиколлинеарности является отбор существенных (информативных) объясняющих переменных. Алгоритмы отбора переменных (базисных функций) отличаются используемым критерием качества набора переменных (базисных функций) и способом генерации набора. Критерии качества являются функциями коэффициента детерминации, объема выборки и количества переменных (базисных функций), входящих в набор. Из схем генерации удобными с вычислительной точки зрения являются пошаговые схемы (STEP-WISE).
Заметим, что пошаговые процедуры применяются и в отсутствие мультиколлинеарности как удобное средство отсеивания незначимых коэффициентов регрессии.
Если возникает задача сопоставить два уравнения регрессии, построенные для двух выборок, то можно воспользоваться тестом Чоу. Пусть 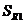 и
и 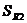 – остаточные суммы квадратов регрессий для первого и второго набора данных,
– остаточные суммы квадратов регрессий для первого и второго набора данных, 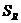 – остаточная сумма квадратов для полной регрессии (объединенная выборка). Если выполняется соотношение
– остаточная сумма квадратов для полной регрессии (объединенная выборка). Если выполняется соотношение
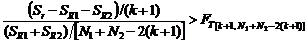 ,
,
то гипотеза H: a 1= a 2 отвергается.
Заметим, что проблема сравнения регрессий может решаться также с использованием фиктивных переменных.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Каковы предпосылки классической регрессии?
2. С помощью каких преобразований исходных переменных можно избавиться от свободного члена в уравнении регрессии?
3. Применим ли метод наименьших квадратов, если число наблюдений меньше числа оцениваемых параметров?
4. Приведите меры мультиколлинеарности. Какая из мер доступна в режиме Multiple Regression?
5. Из двух входных переменных одна менялась прямо пропорционально по отношению к другой. Можно ли доверять результатам работы программы регрессионного анализа в этом случае?
6. Как проверяется адекватность уравнения регрессии?
7. Какие коэффициенты регрессии считаются значимыми?
8. В исследуемом процессе присутствует гармоническая составляющая с заданной частотой, но неизвестной фазой. Каким образом можно свести уравнение регрессии к линейному по параметрам виду?
9. Для целей линеаризации нелинейного по параметрам уравнения регрессии использовались разнообразные преобразования исходных переменных. Какой из характеристик (остаточной суммой квадратов или коэффициентов детерминизации) удобнее воспользоваться?
10. Какие особенности ряда остатков свидетельствуют о возможной неадекватности модели?
11. Что показывает статистика Дарбина -Уотсона? Как ею пользоваться?
ЗАДАНИЕ
Работа состоит из трех частей.
Вначале строится зависимость выходной (целевой) характеристики объекта от одной из входных переменных xi (парная регрессия), а затем линейная модель от всех входных переменных x 1– x n с помощью процедур многомерной (Multiple) и пошаговой (Stepwise) регрессии. В третьей части лабораторнлй работы необходимо построить уравнение регрессии для другого набора данных, а затем проверить полученные уравнения на совпадение.
1. Парная регрессия
1.1. Получить у преподавателя файл исходных данных, на базе которого формируется выборка в соответствии с вариантом (см. Приложение 3).
1.2.Построить совокупность двумерных диаграмм рассеяния, воспользовавшись следующими пунктами меню: Statiatics → Basic Statistic/Tables → Correlation Analysis. В качестве входной переменной выбрать ту, которая оказывает наибольшее влияние на целевую переменную.
1.3.Перейти в модуль регрессионного анализа (Statiatics → Multiple Regression), оценить параметры и построить графики следующих моделей: линейной (Linear) у = а 0+ а 1 х 1, экспоненциальной (Exp) 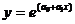 и обратной (Reciprocal) у =1/(а 0+ а 1 х 1).
и обратной (Reciprocal) у =1/(а 0+ а 1 х 1).
1.4.Сравнить полученные модели по R 2 и S 2 и выбрать лучшую.
2. Многомерная регрессия
2.1.Наметить список объясняющих переменных для включения в многомерную линейную модель регрессии.
2.2.Вычислить матрицу коэффициентов сопряженности (корреляции).
2.3.Исследовать набор данных на мультиколлинеарность. Для этого воспользоваться модулем Principal Components ← Multivariate Explotary Techniqes ← Statiatics для вычисления собственных значений.
2.3.Построить многомерную регрессионную модель, включив в начале в нее все объясняющие переменные (характеристики исследуемых объектов) и избавляясь затем от незначимых переменных.
2.4.Проверить гипотезу, что уравнение регрессии является константой.
2.5.Для окончательной модели построить график остатков. Удостовериться по критерию Дарбина-Уотсона, что случайные возмущения некоррелированы.
2.6.Перейти в режим пошаговой регрессии и построить модель прямым и обратным пошаговыми методами.
3. Сравнение регрессий
3.1. Построить регрессию для второй выборки, указанной в варианте задания, теми же базисными функциями, которые присутствовали в адекватном уравнении регрессии п.2 задания.
3.2. Сравнить уравнения: а) по тесту Чоу, б) введением фиктивной переменной со значением 0 для первого набора и значением 1 – для второго. Остаточные суммы квадратов, используемые в тесте Чоу, подсчитываются в блоке дисперсионного анализа (Advanced → ANOVA).
Требования к отчету
Отчет должен содержать:
-таблицы основных статистик для всех рассматриваемых моделей;
-сравнительный анализ результатов одновременного (п.2.3) и пошагового (п.2.5) построения модели;
-сравнительный анализ парной и многомерной моделей с учетом изменений R2 и s2;
-качественный анализ графика остатков на предмет соответствия предпосылкам классической регрессии;
-заключение о существенности мультиколлинеарности исходных переменных.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА [2, 3, 10,12]



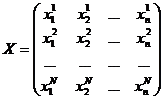
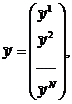
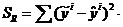
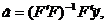
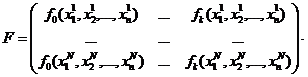
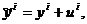
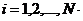
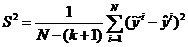
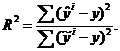

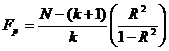

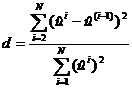
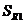 и
и 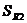 – остаточные суммы квадратов регрессий для первого и второго набора данных,
– остаточные суммы квадратов регрессий для первого и второго набора данных, 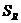 – остаточная сумма квадратов для полной регрессии (объединенная выборка). Если выполняется соотношение
– остаточная сумма квадратов для полной регрессии (объединенная выборка). Если выполняется соотношение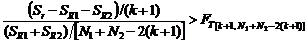 ,
,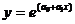 и обратной (Reciprocal) у =1/(а 0+ а 1 х 1).
и обратной (Reciprocal) у =1/(а 0+ а 1 х 1).

