Свойства определенного интеграла
1) Пусть функции f(x) и g(x) интегрируемы на отрезке [ а, b ]. Тогда функции f(x) + g(x) также интегрируемы на этом отрезке, причем
 .
.
2) Если функция f(x) интегрируема на отрезке [ а, b ], то функция kf(x) (где k – постоянная) также интегрируема на этом отрезке, причём
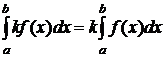 .
.
3) Если функция f(x) интегрируема на отрезке [ а, c ] и [ с, b ], то функция f(x) интегрируема и на отрезке [ а, b ], причём
 .
.
4) Интеграл по симметричному интервалу:
a) f(x) – интегрируемая на интервале [- а, а ] функция, причём f(x) – чётная на нём, тогда
 .
.
b) f(x) – интегрируемая на интервале [- а, а ] функция, причём f(x) – нечётная, тогда
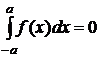 .
.
Оценки интервалов
5) Если функция f(x) интегрируема на интервале [ а, b ] и f(x) > 0 для всех x из [ а, b ], то интеграл от функции f(x) по этому интервалу неотрицателен, т.е.
 .
.
6) Если функции f(x) и g(x) интегрируемы на интервале [ а, b ] и f(x) < g(x) для всех x из [ а, b], то
 .
.
7) Если f(x) интегрируема на интервале [ а, b ], где а < b, и если во всём этом интервале имеет место неравенство m < f(x) < M, где M и m – наибольшее и наименьшее значения функции f(x) в интервале [ а, b ], то
b
m(b – а) < ò f(x) d x < M(b – а)
a
Среднее значение функции на отрезке
8) Определенный интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке x = c отрезка интегрирования [ а, b ] на длину отрезка (b – а):
 , или
, или 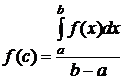
Значение f(c), определяемое по этой формуле, называется средним значением функции f(x) в отрезке [ а, b ].
Формула Ньютона-Лейбница.
Формула Ньютона-Лейбница устанавливает связь между определенным и неопределенным интегралами.
Теорема. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интеграла:
 , где F'(x) = f(x) (1.2)
, где F'(x) = f(x) (1.2)
Эта формула носит название формулы Ньютона-Лейбница.
Способы вычисления определенных интегралов
1) Вычисление определенных интегралов по формуле Ньютона- Лейбница.
Пример 1.10. Вычислить  .
.
Решение.  =
= 
2) Вычисление определенных интегралов с помощью замены переменной.
Пример 1.11. Вычислить интеграл  .
.
Решение. Сделаем подстановку t = 3 + x 2, отсюда d t = 2 x d x.
 = 0,5
= 0,5  = 1/3 t 3/2
= 1/3 t 3/2  = 1/3 (8 – 3
= 1/3 (8 – 3  ) = 8/3 –
) = 8/3 –  .
.
3) Вычисление определенных интегралов с помощью формулы интегрирования по частям

Пример 1.12. Вычислить интеграл  .
.
Решение. Положим u = ln x, отсюда d u = d(ln x) = (1/ x)d x; d v = d x; v = x и по формуле (1.1) находим
 = x ln x
= x ln x  –
–  = (x ·ln(x) – x)
= (x ·ln(x) – x)  = (x (ln(x) – 1)
= (x (ln(x) – 1)  = (e(ln(e) – 1) – (1·0 – 1) = (e – 1) + 1 = e.
= (e(ln(e) – 1) – (1·0 – 1) = (e – 1) + 1 = e.
Применение определенного интеграла
Вычисление площадей плоских фигур
Если функция f(x) непрерывна на отрезке [ a, b ], и f(x) > 0, то площадь криволинейной трапеции, ограниченной линиями y = f(x), x = a, x = b, равна:
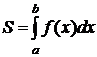 ()
()
Если f(x) ≤ 0, то площадь соответсвующей кривой определяется формулой:
 ()
()
Если кривая y = f(x) пересекает ось 0x, то отрезок [ a, b ] нужно разбить на части, в пределах которых f(x) не меняет знак, и общая площадь будет равна сумме площадей частей.
Пример 1.13. Вычислить площадь фигуры, ограниченной линиями y = x 2 и y = 3 x.
Решение. Искомая площадь представляет собой разность между площадью прямоугольника, ограниченного сверху прямой y = 3 x, и площадью криволинейного треугольника, ограниченного сверху участком параболы (рис. …):
S =  .
.
Абсциссу точки b пересечения графиков находим из уравнения x 2 = 3 x:
x 2 – 3x = 0, x (x – 3) = 0, x 1 = 0, x 2 = 3. Откуда b = 3. Следовательно,

Построение графика функции
Несобственные интегралы
Несобственными называются определенные интегралы, у которых либо пределы интегрирования a и b не являются конечными, либо подынтегральная функция f(x) на отрезке [ a; b ] не является непрерывной. Например,  Если этот интеграл имеет конечный предел, то он называется несобственным сходящимся интегралом и обозначается:
Если этот интеграл имеет конечный предел, то он называется несобственным сходящимся интегралом и обозначается:
 .
.
Значение интеграла определяется по формуле Ньютона- Лейбница:
 . (1.3)
. (1.3)



 .
.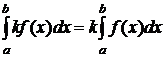 .
. .
. .
.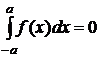 .
. .
. .
. , или
, или 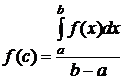
 , где F'(x) = f(x) (1.2)
, где F'(x) = f(x) (1.2) .
.
 .
. = 1/3 t 3/2
= 1/3 t 3/2  = 1/3 (8 – 3
= 1/3 (8 – 3  ) = 8/3 –
) = 8/3 – 
 .
. –
–  = (x ·ln(x) – x)
= (x ·ln(x) – x)  = (x (ln(x) – 1)
= (x (ln(x) – 1) 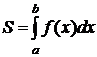 ()
() ()
() .
.

 Если этот интеграл имеет конечный предел, то он называется несобственным сходящимся интегралом и обозначается:
Если этот интеграл имеет конечный предел, то он называется несобственным сходящимся интегралом и обозначается: .
. . (1.3)
. (1.3)


