ВВОДНАЯ ГЛАВА.
Назначение знаковых языковых систем
Язык как инструмент интеллекта
Развитие информационных систем и компьютерных технологий расширили горизонты интеллектуальных возможностей человека. Целью расширения таких возможностей является моделирование функций человеческого интеллекта и, в конечном счёте, автоматизации ряда процессов интеллектуальной деятельности. Что же это такое человеческий интеллект? Согласно энциклопедической информации принято считать, что интеллект – это способность человека реализовать процесс и продукт мыслительной деятельности. В процессе такой деятельности происходит отражение отношения объектов различной природы в виде мыслительных образов. Эти образы составляют субъективный информационный мир личности, а обмен информацией между людьми осуществляется посредством различных языковых систем. Знаковые или символьные языковые системы позволяют каждому индивидууму реализовать мысленную систему образов в виде языковых единиц – слов и их структурных образований – текстов.
Таким образом, мы приходим к пониманию того, что инструментом человеческого интеллекта являются языковые системы.
Функциональные свойства языковых систем
Какую знаковую систему мы можем считать языком?
Впервые определение языка через его функции дал великий математик Леонард Эйлер (1707 – 1763). Он писал: “Язык нужен людям, чтобы они могли следить за своими мыслями и развивать их, а также общаться друг с другом”, [1, с.282]. В связи с этим положением, выдвинутым Л.Эйлером, можно постулировать, что язык как знаковая система проявляется в следующих трёх функциях.
Три основополагающие функции языка, это:
· отслеживание мысли (опорная функция);
· формирование умозаключений (логическая функция);
· средство общения (коммуникационная функция).
Множество человеческих языков как инструментов интеллекта многообразно, это языки музыки, живописи, национальной литературы, языки различных наук, в том числе и математических.
Какую же роль играет каждый язык среди множества языков – инструментов человеческого интеллекта?
Чтобы ответить на этот вопрос, вначале попробуем разобраться в том, как обрабатывает человеческий интеллект поступающую информацию об окружающем его мире. Начальную роль здесь играет взаимодействие опорной и логической языковых функций. Это взаимодействие языковых функций впервые систематически исследовал известный логик конца XIX века Готлоб Фреге (1848 – 1925). Вот его слова: “Нам удаётся управлять нашим вниманием и направлять мысль в желательное для нас русло благодаря знакам. Когда мы воспроизводим знак, то мы тем самым создаём определённую опору нашей мысли, – определённый центр, вокруг которого возникают различные представления. Из этих представлений мы выбираем одно и опять фиксируем его с помощью знака. Так удаётся шаг за шагом проникнуть во внутренний мир наших представлений и двигаться в этом мире в нужном направлении. Чувственно-наглядное (в форме знаков) позволяет нам не потонуть в потоке восприятий и представлений, непрерывно захлёстывающих наше внимание”.
Можно считать, что Фреге открыл «атомарную» структуру мышления в виде дискретных актов, которые формируют циклический процесс организации мыслительных образов из слов в предложения и тексты. Представим этот акт в виде следующей диаграммы, которая отражает процесс мышления как циклическую операцию над образами
Схема 1.1
| Продукт мышления – знаковая единица языка
|
| Реализация в знаковой системе
|
Согласно этой диаграмме, реализацию коммуникационной функции в виде текста можно считать итерацией, т.е. последовательной композицией, таких актов.
3. Определение и примеры языковых систем
Три функции языковой системы можно объединить в определение языковых знаковых систем, представленное в виде следующего файла Ф.1
| Ф.1
| Определение символьного или знакового языка
|
| Знаковая или символьная система, используемая для такой организации структуры мыслительных образов, которая представляет информацию, называется символьным или знаковым языком.
|
Рассмотрим некоторые примеры языковых систем.
Пример 1
Система дискретных звуковых знаков есть общепринятое понятие человеческого языка, являющегося средством общения.
Пример 2
Система последовательностей двух символов 0 и 1 представляет язык числовых кодов: 110001, 100100100, и т.д.
Пример 3. Система жестов или сигналов, при помощи которых передаётся информация: азбука Морзе, морские сигналы при помощи флажков, жестикуляция, при помощи которой общаются глухонемые люди.
Пример 4. Набор цветных красок, позволяющий создавать любые сочетания цветов и рисовать художественные картины.
Пример 5. Система знаков представляющих музыкальные звуки называется нотами и формирует язык музыки.
| Ф.2
| Нотные знаки гаммы целых звуков одной октавы
|
|
|
Пример 6. Система направленных отрезков формирует язык векторов в геометрии и физике.
Пример 7. Десятичная системазнаков формирует язык действительных чисел.
Пример 8. Система дорожных знаков не является языком. В этой знаковой системе присутствует опорная функция, но отсутствует логическая функция, которая позволяет строить умозаключения.
Основные языковые понятия
Языковой способ коммуникации, то есть передачи информации, основан на композиции знаковых единиц – потоке слов, организованных в предложения – тексты. Приведём те языковые понятия, при помощи которых формируется понятие текста любого языка в виде следующих файлов.
| Ф.3
| Определение формального слова
|
| Языковую знаковую или символьную единицу, представляющую мыслительный образ, назовём формальным словом
|
| Ф.4
| Определение формального предложения
|
| Упорядоченное множество формальных слов, несущее в себе информацию законченного характера, назовём формальным предложением.
|
| Ф.5
| Определение формального текста
|
| Последовательность формальных предложений, синтезирующая информационный поток, назовём формальным текстом.
|
Тексты, организованные в самостоятельные блоки, как это сделано выше, назовём файлами.
| Ф.6
| Определение файла
|
| Текст
|
Файлы несут свой мыслительный образ, и поэтому их можно использовать для организации более сложных, нелинейных текстовых структур: каталогов, диаграмм, блок-схем и т.д., например, Схема 1, приведённая выше. Ещё пример – формирование понятия символьного языка в виде следующей блок-схемы:
Вывод.
Сущность языковых систем состоит в том, что закономерности интеллектуальной деятельности, отражающие мыслительные процессы в некоторой предметной области, реализуются в законах организации текстовых структур, несущих специфику данной предметной области.
А каковы общие закономерности знаковых языковых систем, представляющих интеллектуальную продукцию в текстовой форме? Имеют ли они общую природу независимо от предметной области?
Ответы на эти вопросы невозможны без анализа современных научных направлений, синтезированных исследованиями в психологии, лингвистике, математике, физики информационных процессов и др. и фактически подводит нас к проблеме моделирования смысловых отношений в знаковых системах, представляющих тексты.
В историческом плане работа в этом направлении только начинается. Впереди – открытия, которые помогут нам осознать закономерности функционирования интеллектуальных систем посредством изучения текстовых структур – основного интеллектуального продукта. С современным состоянием исследований в этом направлении можно познакомиться по трудам научных конференций, ссылки на которые можно найти в интернете по ключевым словам.
Вопросы.
1. Какими функциями, по Эйлеру, определяются языковые знаковые системы?
2. Как соотносятся между собой интеллект и мышление человека?
3. Что является аналогом слова, предложения и текста в музыкальной грамоте?
4. Что является аналогом слова, предложения и текста в живописи?
Задания.
1. Покажите, что в примерах 1-7 пункта 1.3 приведены языковые знаковые системы.
2. Приведите примеры знаковых систем, не являющихся языками.
3. Обоснуйте положение «язык – инструмент интеллекта и мышления»
“Господь Бог создал натуральные числа; все остальное дело рук человеческих”.
Леопольд Кронекер (1823-1891)
ГЛАВА I
Система натуральных чисел.
Человек обладает способностью образно различать количества предметов и представлять количественные образы в знаковой, или символьной, системе. Эта способность отражает свойство нашего интеллекта, которое мы называем умением считать или перечислять, а соответствующая символьная реализация этого процесса называется натуральным рядом.
Попробуем дать определение натурального ряда на русском языке, переведём это определение на английский, затем ещё на какой-нибудь язык и снова – на русский. К своему удивлению мы обнаружим, что получили новый текст, не вполне идентичный исходному. Несложно догадаться, что произошло. При переводе с другого языка мы подбираем слова, используя представителей класса синонимов, а математика использует слова как знаковые единицы, несущие вполне конкретный смысл. Чтобы избежать многозначности языкового толкования понятия «натуральный ряд», математики поступили следующим образом. Свойство человеческого интеллекта «перечислять объекты» рассматривается как функция интеллекта, сама же функция определяется наименьшим набором правил, которые полностью описывают действие этой функции. Чтобы найти искомые правила, построим файл, определяющий эмпирические, то есть опытные, способности человека, на которых основано построение интересующей нас знаковой системы натурального ряда.
| Ф.1.
| Эмпирические свойства, определяющие построение натурального ряда
|
| 1о. Любой объект может быть выбран начальным элементом перечисления.
2о. Для любого количества перечисленных элементов определено единственное следующее за ним количество.
3о. начальному элементу не предшествует никакое количество.
4о. Двум одинаковым количествам предшествуют два одинаковых количества.
5о. Построенное множество количеств однозначно в том смысле, что все другие построенные таким образом количества совпадают и могут отличаться только символьными системами.
|
Теперь займемся формализацией перечисленных свойств. Это означает, что требуется построить систему аксиом (правил), отражающих перечисленные в файле операции 1о-5о в символьной форме.
Дадим символьную реализацию операций 1о-5о. Свойство 1о позволяет выбрать первый элемент, обозначим его 1. Свойство 2о устанавливает операцию следования на множестве элементов. Эту операцию представим в виде схемы
… → x → s(x) → … (1.1)
Заметим, что свойству 2о также удовлетворяет схема
… → x → s(x) → …
→ y (1.2)
Свойство 4о указывает, что схема (1.2) реализоваться не может. Свойство 3о устанавливает единственность первого элемента, и мы приходим к линейной цепочке
1 → s(1) → … → x → s(x) → … (1.3)
Эта цепочка образует «очередь», или, что, то же самое, линейный порядок. Последнее свойство 5о утверждает, что всякая другая линейная цепочка со свойствами 1о-4о будет отличаться только знаковой системой
1 → a → … → b → g → …
При этом порядок следования и количество операций следования, необходимых для достижения данного элемента, не изменятся. Это означает, в частности, что если знак, обозначающий количество пять, следует за знаком количества четыре, то это свойство не зависит от того, в какой знаковой системе оно выражено.
Приведем в немного измененном виде систему аксиом Джузеппе Пеано (1858-1932), формализующую построение правил, записанных в файле Ф.1. При этом каждую аксиому сформулируем подробно и представим кратко на языке символов формальной логики, принятых в международной практике (см. обозначения на стр. 97).
| Ф.2.
| Система правил, формирующих натуральный ряд.
|
| Множество символов, элементы которого удовлетворяют следующим свойствам 1о-5о, называется натуральным рядом N.
|
| 1о. Некоторый элемент называется первым и обозначается символом 1:
$ x (x:= 1).
|
| 2о. Для всякого элемента x существует единственный элемент S(x) следующий за x:
"x $ y (y = S(x))
"x, y (y = x Þ S(x) = S(y)).
|
| 3о. Единице не предшествует никакой элемент:
"x (S(x) ¹ 1)
|
| 4о. Всякому элементу предшествует единственный элемент:
"x, y (S(x) = S(y) Þ x=y)
|
| 5о. Аксиома индукции. Пусть подмножество ΜÌΝ содержит 1, и для его элементов x выполняются свойства 2о-4о (обозначим выполнение свойств 1о-4о T(x)). Тогда Ν Ì Μ.
|
| "x (xÎM)L(T(x)) Þ M=N
|
Заметим, что из этой системы правил нельзя выбросить ни одно. Попробуем, например, выбросить пятое правило. Для этого рассмотрим знаковую модель, предложенную норвежским математиком Торальфом Сколемом (1887-1963). К линейной цепочке (1.3) добавляются последовательности блоков вида
…→ a-2 → α-1 → α-0 → α1 → a2 → …
тогда в новой цепочке найдутся новые элементы, которые нельзя представить в виде конечного числа операций S. То есть, найдутся элементы “ y ” модели Сколема, которые не удовлетворяют условию
y = S (S (…S (1))),
где S (S (…S (1))) - конечное число композиций операции следования.
Такие элементы y назовем недостижимыми. Таким образом, наличие правил 1-4 позволяет построить только линейный порядок - очередь, но элементы этой очереди могут оказаться недостижимыми.
В школьной программе математики натуральный ряд строится в десятичной модели 1, 2, 3,…, n, n+1, …, в ней свойство конечной достижимости выполняется, т.к. десятичная запись содержит информацию о порядке числа. Десятичная система использует конечный цифровой алфавит 0, 1, 2, …, 9. Суть построения символа целого числа в этой системе в том, что вводятся операции сложения и умножения, и закон записи имеет вид " a Î N
a = a n a n-1… a 1 a 0 = a n˙ 10 n + a n-1˙ 10 n-1 + …+ a 1˙ 10 + a 0 ,
где a 0, a 1, …, a n Î(0, 1, …, 9)Ù(a n ¹0).
Поскольку операции сложения и умножения ранее не фигурировали в модели Ф.2, то для построения десятичной записи элементов натурального ряда следует добавить аксиомы, определяющие операции сложения, умножения и свойства этих операций.
Добавляя к аксиоматике натурального ряда новые операции вместе с определяющими их аксиомами, мы не только расширяем свойства натурального ряда, но и расширяем само множество натуральных чисел. Рассмотрим этот процесс подробнее.
Вывод 1.
Множество чисел, представимых в виде несократимых дробей m / n, где: m, n, 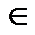 N, n
N, n 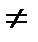 0 называется множеством рациональных чисел и обозначается Q. На этом множестве определены операции ±, ´,:, ≤, и результат действия этих операций над рациональными числами есть снова рациональное число.
0 называется множеством рациональных чисел и обозначается Q. На этом множестве определены операции ±, ´,:, ≤, и результат действия этих операций над рациональными числами есть снова рациональное число.
Мы не будем обсуждать все свойства рациональных чисел, а ограничимся напоминанием свойств систематического представления рациональных чисел, известных из элементарного курса математики.
Наличие операций сложения и умножения позволяет построить представление целых чисел при помощи алфавита, содержащего К знаков, называемых цифрами.
Такое представление дается записью вида:  a
a 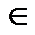 N
N
a = anKn+... + a1K+ao (1.4)
и называется систематической К -ичной записью по основанию К. Символы ao, a1,..., an принимают одно из К значений 0,1,2,..., K-1. Если K 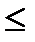 10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2,..., К-1. Для обозначения степеней оснований (классов) К1, К2,..., Кn используются уже введенные числовые обозначения (классы “тиражируются” медленнее, чем числа, входящие в эти классы).
10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2,..., К-1. Для обозначения степеней оснований (классов) К1, К2,..., Кn используются уже введенные числовые обозначения (классы “тиражируются” медленнее, чем числа, входящие в эти классы).
Запись целых чисел в K- ичной системе позволяет реализовать арифметические операции над рациональными числами в виде некоторых алгоритмов (известных в элементарной математике как правила «действий столбиком»), то есть правил выполнения последовательности простых операций над цифрами, представляющими рациональные числа.
В школьном курсе изучаются алгоритмы арифметических операций в десятичной системе.
Напомним для примера алгоритм сложения целых чисел.
Пусть а = 247 = 2 . 102 +4 . 10+7, b = 378 = 3 . 102 + 7 . 10 + 8. Требуется найти c = а+b.
Складывая цифры, нумерующие разряды единиц, десятков и сотен, получаем:
7+8 = 10+5 (единицы)
4.10 + 7 . 10 = 102+10 (десятки)
2 . 102 + 3 . 102 = 5 . 102 (сотни)
Учитывая правила формирования разрядов, составляем десятичную запись числа c = а+в:
c = (102 +5 . 102) + (10+10)+5 = 6. 102 +2 . 10+5 = 625
Кроме реализации арифметических операций, систематическое представление чисел дает алгоритм сравнения чисел по величине.
Для сравнения целых положительных чисел достаточно сравнить цифры разрядов по старшинству, например: 197<211, так как 197<2.102, а 211 > 2.102.
Алгоритм представления рационального числа  в десятичной записи приводит к двум типам записи чисел, известным из школьного курса.
в десятичной записи приводит к двум типам записи чисел, известным из школьного курса.
Всякое рациональное число может быть представлено конечной десятичной дробью вида:
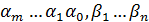 =
= 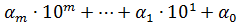 +
+ 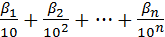 , (1.5)
, (1.5)
либо бесконечной периодической дробью вида:
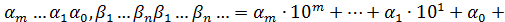
+ 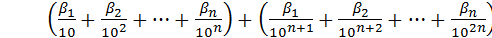 (1.6)
(1.6)
 Напомним также, что алгоритм десятичного представления рационального числа в виде (1.5) или (1.6) основан на следующем свойстве целых чисел:
Напомним также, что алгоритм десятичного представления рационального числа в виде (1.5) или (1.6) основан на следующем свойстве целых чисел:
для любых a,b 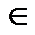 N, (a > b) существуют m, n
N, (a > b) существуют m, n 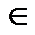 N, (m<a, n<b) такие, что
N, (m<a, n<b) такие, что
а = bm+n (1.7)
Замечание 1.
Запись рациональных чисел в виде (1.6) требует обоснования, которое заключается в объяснении сходимости числового ряда, т.е. существования конечного числа, являющегося результатом бесконечного суммирования в следующей записи:
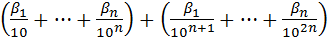 +...+
+...+ 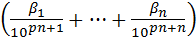 +...(1.8)
+...(1.8)
Объяснение того, что эта сумма представляет рациональное число, основано на том, что эта сумма есть сумма бесконечно убывающей геометрической прогрессии. Например, число 0,123123123… являющееся бесконечной периодической дробью преобразуется в запись p/q следующим образом:
0,123123... = 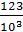 +
+ 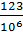 +... =
+... = 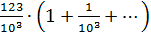 =
= 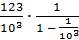 =
= 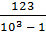 =
= 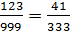
Здесь мы воспользовались формулой суммы бесконечно убывающей геометрической прогрессии:
a + aq + aq 2 + … = 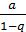 , q <1,
, q <1,
где в нашем примере a = 1, q = 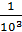 .
.
Определение 1.
Множество Q называется множеством рациональных чисел, а его элементы - рациональными числами, если выполняется следующий комплекс условий, называемый аксиоматикой рациональных чисел:
Аксиомы операции сложения.
Для всякой упорядоченной пары х,у элементов из Q определен некоторый элемент х+у Î Q, называемый суммой х и у. При этом выполняются следующие условия:
1. (Существование нуля) Существует элемент 0 (нуль) такой, что для любого х Î Q
х + 0 = 0 + х = х.
2. Для любого элемента х Î Q существует элемент - х Î Q (противоположный х) такой, что
х + (-х) = (-х) + х = 0.
3. (Коммутативность) Для любых х,у Î Q
 х + у = у + х
х + у = у + х
4. (Ассоциативность) Для любых х, у, z Î Q
х + (у + z) = (х + у) + z
Аксиомы операции умножения.
Для всякой упорядоченной пары х,у элементов из Q определен некоторый элемент ху Î Q, называемый произведением х и у. При этом выполняются следующие условия:
5. (Существование единичного элемента) Существует элемент 1Î Q такой, что для любого х Î Q
х ×1 = 1× х = х
6. Для любого элемента х Î Q, (х¹ 0) существует обратный элемент х -1 ¹ 0 такой, что
х×х -1 = х-1×х = 1
7. (Ассоциативность) Для любых х, у, z Î Q
х× (у× z) = (х× у)× z
8. (Коммутативность) Для любых х, у Î Q
х × у = у× x
Аксиомы порядка.
Всякие два элемента х, у, Î Q вступают в отношение сравнения £. При этом выполняются следующие условия:
10. (х 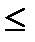 у) Ù (у
у) Ù (у 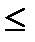 x)
x)  x = у
x = у
11. (х 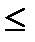 у) Ù (у
у) Ù (у 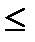 z)
z) 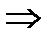 x
x 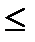 z
z
12. Для любых х, у Î Q либо х < у, либо у < x.
Отношение < называется строгим неравенством,
Отношение = называется равенством элементов из Q.
Следствие.
Аксиомы множества рациональных чисел Q позволяют:
1. Построить систематическую запись рациональных чисел при помощи конечного алфавита (цифровых символов) в виде К -ичной системы.
2. Определить алгоритмы реализации операций ±, ´,:, £ в систематической записи рациональных чисел в выбранной К -ичной системе.
Задача 1.
Измерить длину диагонали квадрата, считая, что единица длины есть сторона этого квадрата.
Теорема Пифагора дает результат: искомая длина равна 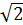 . Предположение о том, что
. Предположение о том, что 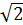 = p / q – несократимая рациональная дробь опровергается известным доказательством от противного. Предположим, что
= p / q – несократимая рациональная дробь опровергается известным доказательством от противного. Предположим, что 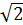 = p / q, тогда p 2= 2 q 2, откуда следует, что p =2 k. Поэтому 2 q 2= 4 k 2Þ q = 2 m. Следовательно,
= p / q, тогда p 2= 2 q 2, откуда следует, что p =2 k. Поэтому 2 q 2= 4 k 2Þ q = 2 m. Следовательно, 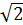 =2 k /2 m, что противоречит предположению, что исходная дробь несократима. Этот факт был известен ещё Пифагору.
=2 k /2 m, что противоречит предположению, что исходная дробь несократима. Этот факт был известен ещё Пифагору.
Задача 2.
Измерить длину окружности, считая, что диаметр этой окружности есть единица длины.
Длина окружности L = 2 pR, где R – радиус. В нашем случае L =3,1415…. Число p не является рациональным. То, что число p не является рациональным числом, впервые было установлено в 1761 г. французским математиком Иоганном Генрихом Ламбертом (1728 – 1777).
Вывод 2.
Существуют числа, не представимые в виде p / q ни для каких целых p, q.
Эти числа не являются результатом конечного числа арифметических операций над целыми числами, в противном случае можно было бы указать процедуру их вычислений за конечное число шагов.
Числа, не представимые в виде p / q ни для каких целых p, q, называются иррациональными.
Вывод 3. К понятию иррациональных чисел мы пришли в результате задач обычного измерения отрезков. А именно, мы решили результату измерения отрезка сопоставить определённое число. Оказалось, что множества рациональных чисел, вполне достаточного для реализации арифметических операций, выполняемых над заданным единичным отрезком, недостаточно для того, чтобы представить результат измерения произвольного отрезка.
Геометрически данная ситуация изображается на рисунках 1.1 и 1.2.
0 1 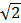 х х
|
Рис.1.1 Рис.1.2
На рис.1 на оси ОХ согласно решению задачи 1 отложен отрезок равный диагонали квадрата с единичной стороной, конец этого отрезка отмечен символом 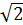 . На рис.2 на оси ОХ согласно задаче 2 отложен отрезок равный длине окружности с единичным диаметром. Конец этого отрезка отмечен символом p. Эта точка является образом точки О: если окружность прокатить вправо один раз по оси ОХ, то точка О совместится с точкой p.
. На рис.2 на оси ОХ согласно задаче 2 отложен отрезок равный длине окружности с единичным диаметром. Конец этого отрезка отмечен символом p. Эта точка является образом точки О: если окружность прокатить вправо один раз по оси ОХ, то точка О совместится с точкой p.
Таким образом, обычные задачи измерения отрезков потребовали расширить понятия рациональных чисел до понятия иррациональных чисел.
Определение 2.
Множество R называется множеством действительных чисел, а его элементы действительными числами, если они удовлетворяют всем тем же аксиомам 1-15, что и рациональные числа и, дополнительно, аксиоме непрерывности Кантора.
Задача 3.
Построить символьную запись действительных чисел, в которой: а) допустимо измерение длины любого отрезка, б) реализуются арифметические операции над действительными числами.
Мы покажем, что запись действительных чисел в десятичной системе является подходящей для этой цели.
Нам потребуется понятие взаимно-однозначного соответствия множеств.
Определение взаимно-однозначного соответствия. Будем говорить, что между элементами х множества Х и элементами у множества У установлено взаимно-однозначное соответствие у = f (x), если каждому х из Х соответствует единственный у из У и наоборот, для каждого у из У существует единственный х из Х такой, что у = f (x).
Для решения задачи а) достаточно установить, что между точками прямой и действительными числами в десятичной записи существует взаимно-однозначное соответствие. Для простоты ограничимся записью чисел x Í [0,1]. Пусть точка М –произвольная точка единичного отрезка прямой. Разобьём этот отрезок на 10 равных частей и пронумеруем эти отрезки цифрами 0, 1, 2, …,9, разместив их с левой стороны отрезков, рис 1.3
Рис. 1.3.
Если точка М попала в отрезок под номером  где
где  одно из чисел0,1,2, 3, …, 9, то этой точке на данном этапе построения сопоставим число х = 0,
одно из чисел0,1,2, 3, …, 9, то этой точке на данном этапе построения сопоставим число х = 0,  и разделим этот
и разделим этот  - отрезок снова на десять равных частей, рис. 1.4. Точка М окажется в каком-то отрезке под номером
- отрезок снова на десять равных частей, рис. 1.4. Точка М окажется в каком-то отрезке под номером  , лежащем в предыдущем отрезке, и мы напишем х = 0,
, лежащем в предыдущем отрезке, и мы напишем х = 0,  ,
,
Рис. 1.4.
Продолжая этот процесс, мы можем оказаться в одной из следующих трёх ситуаций.
1) На n - ном этапе этого процесса точка М совпадёт с риской, разделяющей два смежных отрезка. Выберем для нумерации левый отрезок и закончим процесс построения координаты точки М. В этом случае точке М будет соответствовать координата
х = 0,  …
…  ,
,
имеющая конечную десятичную запись и являющаяся рациональным числом.
2) Точка М никогда не совпадёт с риской деления, процесс построения приведёт к бесконечной десятичной записи, в которой с некоторого места возникают периодические блоки вида  …
…  . В этом случае точке М ставится в соответствие координата в виде бесконечной периодической десятичной дроби (для простоты мы выписали случай, когда блоки стали повторяться с самого начала)
. В этом случае точке М ставится в соответствие координата в виде бесконечной периодической десятичной дроби (для простоты мы выписали случай, когда блоки стали повторяться с самого начала)
х = 0,  …
… 
 …
…  …
…  …
…  …
…
Как мы видели при построении рациональных чисел в п.1.2, эта запись так же представляет рациональное число.
3) Процесс построения приведёт к бесконечной непериодической десятичной записи, в которой нет повторяющихся блоков. Десятичной записью координаты точки М будет запись
х = 0,  …
…  …
…
которую назовём бесконечной непериодической десятичной дробью. В этом случае число х является иррациональным.
Таким образом, мы исчерпали все возможные появления десятичного адреса заданной точки М. Теперь надо проверить, что бесконечная десятичная запись определяет некоторое число. Для периодических дробей мы этот факт установили. Для непериодических дробей существование числа следует из оценки
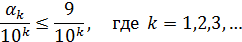
Применяя эту оценку, получим
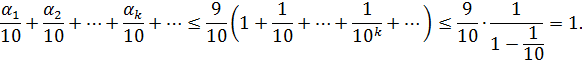
Таким образом, запись вида х = 0,  …
…  определяет число, меньшее единицы.
определяет число, меньшее единицы.
Замечание 2. В построении координат точки М мы воспользовались следующим свойством прямой. Последовательность вложенных друг в друга отрезков прямой при условии уменьшения их длин (на k -том шаге нашего процесса длина промежутка равна 1/10 k) стягиваются к точке и эта точка единственна. Такое свойство прямой мы увидим при формировании аксиоматики геометрии Евклида в следующем параграфе.
Итак, для произвольной точки единичного отрезка мы построили её числовое значение в виде конечной или бесконечной десятичной записи.
Теперь решим обратную задачу. Покажем, что каждой из возможных записей действительного числа в десятичной системе соответствует некоторая точка М на прямой. Для этого десятичную запись рассмотрим как адрес этой точки на прямой. Первый знак  в десятичной записи х = 0,
в десятичной записи х = 0,  …
…  укажет положение точки М с точностью до 1/10, два знака
укажет положение точки М с точностью до 1/10, два знака  , определят точку М с точностью до 1/100, и так далее. Запись х = 0,
, определят точку М с точностью до 1/100, и так далее. Запись х = 0,  …
…  с n знаками после запятой определят точку М с точностью до 10- n. Если десятичная дробь конечна, то мы получим точное положение точки М. Если десятичная запись бесконечна, то процесс сужения промежутка нахождения точки теоретически может продолжаться до как угодно малого промежутка. Тогда согласно аксиоме Кантора (16-той в списке аксиом действительных чисел) найдётся общий элемент для всех промежутков и этот элемент является действительным числом.
с n знаками после запятой определят точку М с точностью до 10- n. Если десятичная дробь конечна, то мы получим точное положение точки М. Если десятичная запись бесконечна, то процесс сужения промежутка нахождения точки теоретически может продолжаться до как угодно малого промежутка. Тогда согласно аксиоме Кантора (16-той в списке аксиом действительных чисел) найдётся общий элемент для всех промежутков и этот элемент является действительным числом.
Теперь обратимся к решению задачи б) о реализации арифметических операций над числами в десятичной записи. Если число является рациональным и имеет конечную десятичную запись, то все арифметические операции выполняются по правилу действия «столбиком» известным из школьного курса. Если число записывается бесконечной дробью, то в случае рационального числа можно вернуться к записи  и проделать с ним арифметические операции. Если число иррациональное или рациональное с очень большим периодом, то оно заменяется близким рациональным числом с конечной десятичной записью и над ним совершаются операции по правилу «столбика». Какова будет потеря точности вычислений при замене бесконечной десятичной дроби конечной её частью? Рассмотрим десятичные приближения. Пусть m / n = a 0, a 1… ak – десятичное приближение с k знаками после запятой числа a = a 0, a 1… akak +1…. Тогда погрешность этого приближения определяется разностью:
и проделать с ним арифметические операции. Если число иррациональное или рациональное с очень большим периодом, то оно заменяется близким рациональным числом с конечной десятичной записью и над ним совершаются операции по правилу «столбика». Какова будет потеря точности вычислений при замене бесконечной десятичной дроби конечной её частью? Рассмотрим десятичные приближения. Пусть m / n = a 0, a 1… ak – десятичное приближение с k знаками после запятой числа a = a 0, a 1… akak +1…. Тогда погрешность этого приближения определяется разностью:
| a – m / n | = ak +1/10 k +1 + ak +2/10 k +2 + … < 9/10 k +1(1 + 1/10 +…) =
= 9/10 k +1´1/(1–1/10) = 1/10 k
Любые практические измерения и вычисления имеют разумный предел точности, который устанавливается, исходя из реальных потребностей. Поэтому, выбирая достаточно хорошее приближение числа с длинной десятичной записью числом с разумно короткой десятичной записью, мы реализуем арифметические операции с необходимой точностью.
Замечание 3.
Можно поставить следующую задачу: построить такое представление действительных чисел, в котором иррациональные числа приближаются рациональными числами наилучшим образом. Рациональная дробь p / q приближает иррациональное число a наилучшим образом, если для любого рационального числа m / n с n £ q выполняется равенство |a– p / q | < |a– m / n |.
Для приближений лучших, чем десятичные приближения используются представление числа цепной дробью, [6]. Если p / q - конечная цепная дробь, приближающая число a, то [2], стр. 46, |a– p / q | < 1/ q 2.
Таким образом, представление числа цепной дробью «более экономично», чем представление десятичной дробью.
Эффективные алгоритмы арифметических операций для представлений чисел в виде цепных дробей до сих пор не найдены, [2], стр. 29-30.
Вопросы.
1. Какую роль играет аксиома индукции в аксиоматике натурального ряда Д. Пеано?
2. Объясните, почему языка рациональных чисе



 N, n
N, n 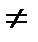 0 называется множеством рациональных чисел и обозначается Q. На этом множестве определены операции ±, ´,:, ≤, и результат действия этих операций над рациональными числами есть снова рациональное число.
0 называется множеством рациональных чисел и обозначается Q. На этом множестве определены операции ±, ´,:, ≤, и результат действия этих операций над рациональными числами есть снова рациональное число. a
a 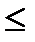 10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2,..., К-1. Для обозначения степеней оснований (классов) К1, К2,..., Кn используются уже введенные числовые обозначения (классы “тиражируются” медленнее, чем числа, входящие в эти классы).
10, то для обозначения K цифр используют первые К цифр десятичной системы 0,1,2,..., К-1. Для обозначения степеней оснований (классов) К1, К2,..., Кn используются уже введенные числовые обозначения (классы “тиражируются” медленнее, чем числа, входящие в эти классы). в десятичной записи приводит к двум типам записи чисел, известным из школьного курса.
в десятичной записи приводит к двум типам записи чисел, известным из школьного курса.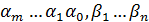 =
= 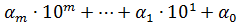 +
+ 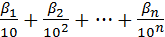 , (1.5)
, (1.5)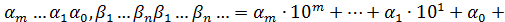
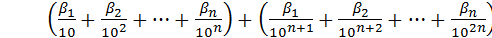 (1.6)
(1.6) Напомним также, что алгоритм десятичного представления рационального числа в виде (1.5) или (1.6) основан на следующем свойстве целых чисел:
Напомним также, что алгоритм десятичного представления рационального числа в виде (1.5) или (1.6) основан на следующем свойстве целых чисел: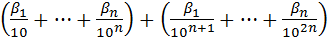 +...+
+...+ 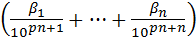 +...(1.8)
+...(1.8)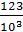 +
+ 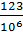 +... =
+... = 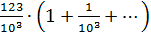 =
= 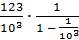 =
= 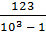 =
= 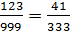
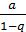 , q <1,
, q <1,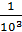 .
. х + у = у + х
х + у = у + х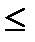 у) Ù (у
у) Ù (у  x = у
x = у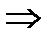 x
x 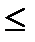 z
z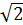 . Предположение о том, что
. Предположение о том, что 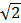 х
х
 где
где  одно из чисел0,1,2, 3, …, 9, то этой точке на данном этапе построения сопоставим число х = 0,
одно из чисел0,1,2, 3, …, 9, то этой точке на данном этапе построения сопоставим число х = 0,  и разделим этот
и разделим этот  ,
, …
…  ,
, …
… 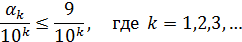
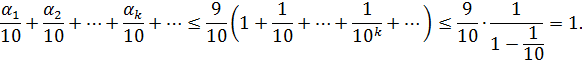
 определяет число, меньшее единицы.
определяет число, меньшее единицы. укажет положение точки М с точностью до 1/10, два знака
укажет положение точки М с точностью до 1/10, два знака  и проделать с ним арифметические операции. Если число иррациональное или рациональное с очень большим периодом, то оно заменяется близким рациональным числом с конечной десятичной записью и над ним совершаются операции по правилу «столбика». Какова будет потеря точности вычислений при замене бесконечной десятичной дроби конечной её частью? Рассмотрим десятичные приближения. Пусть m / n = a 0, a 1… ak – десятичное приближение с k знаками после запятой числа a = a 0, a 1… akak +1…. Тогда погрешность этого приближения определяется разностью:
и проделать с ним арифметические операции. Если число иррациональное или рациональное с очень большим периодом, то оно заменяется близким рациональным числом с конечной десятичной записью и над ним совершаются операции по правилу «столбика». Какова будет потеря точности вычислений при замене бесконечной десятичной дроби конечной её частью? Рассмотрим десятичные приближения. Пусть m / n = a 0, a 1… ak – десятичное приближение с k знаками после запятой числа a = a 0, a 1… akak +1…. Тогда погрешность этого приближения определяется разностью:

