Понятие «фаза» характеризует гармоническое (синусоидальное) колебание в любой конкретный момент времени. Для гармонического колебания u1(t) = Um1sin(wt +j) с амплитудой Um1 и круговой частотой w текущая (мгновенная) фаза в момент времени t равна
j(t) = ωt + j1,
где j1 — начальная фаза.
Фазовым сдвигом Dj двух гармонических сигналов одинаковой частоты u1(t) = Um1sin(wt +j1) и u2(t) = Um2sin(wt +j2) называется модуль разности их начальных фаз:
Dj = | j1 - j2 |, (3.14)
Собственно же величина Dj = j1 - j2 называется разностью фаз сигналов. Фазовый сдвиг Dj не зависит от времени, если остаются неизменными начальные фазы j1 и j2.
Отметим, что на практике обычно решают задачу измерения разности фаз двух гармонических (синусоидальных) колебаний с равными частотами. Фазовый сдвиг удобнее представить как зависимость сдвига сигналов во времени Dt, соответствующего их идентичным фазам. Так, например, для синусоидальных сигналов u1(t) = Um1sinwt и u2(t) = Um2sinw(t-Dt), имеющих одинаковый период Т= 2p/w — сдвиг фазы (рис. 12.1, а) равен
Dj = wDt = 2pDt/T. (3.15)
Два сигнала называются синфазными, противофазными и находящимися в квадратуре, если фазовый сдвиг между ними равен 0, p и p/2 соответственно. Применительно к периодическим синусоидальному и несинусоидальному сигналам (рис. 12.1, б) и к двум несинусоидальным сигналам с одинаковым периодом Т используется понятие об их сдвиге (задержке) во времени Dt.

Рис. 3.7. Графики сигналов: а - двух синусоидальных;
б - синусоидального и несинусоидального с одинаковым периодом
Для измерения фазового сдвига используются приборы, называемые фазометрами, а в качестве мер такого сдвига — фазовращатели, т.е. линейные четырехполюсники, у которых выходной сигнал задержан по фазе относительно входного. Существуют регулируемые и нерегулируемые фазовращатели.
3.2
Методы измерения фазового сдвига
К основным методам измерения фазового сдвига относятся:
- осциллографический,
- компенсационный,
- преобразования фазового сдвига в импульсы тока,
- дискретного или цифрового счета,
- с преобразованием частоты.
Осциллографический метод
Для измерения фазового сдвига с помощью осциллографа применяются следующие методы:
- линейной развертки,
- синусоидальной развертки,
- круговой развертки,
- метод полуокружности.
Метод линейной развертки реализуется при наблюдении на экране одновременно двух сигналов (см. рис. 12.1). Для этого можно использовать двухлучевой осциллограф, подавая сигналы на входы вертикального отклонения лучей (входы Y). Можно также применить однолучевой осциллограф, если на его вход Y подавать исследуемые сигналы поочередно через электронный коммутатор. В том и другом вариантах горизонтальные развертки осциллографов должны быть синхронизированы одним из сигналов. Измерив временные отрезки Dt и Т, вычисляют фазовый сдвиг сигналов в радианах по формуле (12.2) или в градусах по следующему выражению:
Dj = 360 ° Dt/T. (3.16)
При данном методе погрешность измерения фазового сдвига Dj близка к ±(5...7)° и вызвана нелинейностью развертки, неточностью замера интервалов Dt и Т, а также ошибками определения положения оси времени.
Метод синусоидальной развертки или эллипса
Реализуется с помощью однолучевого осциллографа при подаче одного сигнала на вход Y, а второго — на вход X отклонения луча. При этом генератор развертки осциллографа должен быть выключен.
Пусть на входы X и Y были поданы соответственно сигналы u1(t) = u1= Um1sin(wt) и u2(t) = u2 = Um2sin(wt +j), для которых фазовый сдвиг Dj = j (далее в выражениях для u1(t) и u2(t) аргумент t везде опущен). Мгновенные отклонения луча на экране по горизонтали и вертикали равны:
х = hxUm1sinwt = asinwt,(3.17)
y = hyUy2sin(wt +j) = b sin(wt +j), (3.18)
где коэффициенты hx, hy — чувствительности осциллографа к отклонению луча по горизонтали и вертикали; а = hxUm1, b = hyUy2 — амплитуды отклонения луча.
Для определения формы фигуры, вычерчиваемой лучом на экране осциллографа, найдем ее аналитическую запись. Для этого достаточно исключить из формул (12.4) и (12.5) переменную t и затем представить отклонение у в зависимости от величины х:
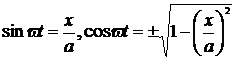 , (3.19)
, (3.19)
y = b sin(wt +j) = b (sinwt cosj +coswt sinj), (3.20)
После подстановки (12.6) в (12.7) получим выражение
 , (3.21)
, (3.21)
представляющее собой известное уравнение эллипса (рис. 12.2).

Рис. 3.7. К измерению разности фаз методом эллипса
Определим величину фазового сдвига двух сегментов. Частям эллипса, представленным непрерывной и штриховой линиями (рис. 12.2), соответствует уравнение (12.8), в котором перед корнем стоят знаки плюс и минус соответственно. Величины отрезков у0 и х0 находятся по уравнению (12.8), если положить для непрерывной линии х = 0, а для штриховой у = 0:
у0 = bsinw,х0 = asinw.
Отсюда искомый фазовый сдвиг:
 , (3.22)
, (3.22)
Перед началом измерения Dj обычно уравнивают на экране амплитуды b и а (рис. 12.2). Для этого поочередно отключают сигналы u1 и u2 от входов X и Y и с помощью регулировок чувствительности hx или hy добиваются равенства b = а, когда у0 = х0. Измерив на экране отрезки 2 у0 и 2 b (или 2 х0 и 2 а), подставляют их отношение в формулу (12.9) и вычисляют Dj.
Метод эллипса не позволяет однозначно определить фазовый сдвиг в диапазоне (0...360)0. Это наглядно видно из осциллограмм, представленных на рис. 12.3, соответствующих различным значениям Dj.
Добиться достаточно точного результата измерений сдвига фаз можно, подав один из сигналов на осциллограф через фазовращатель на 90° и проследив за изменением вида осциллограммы. Положим, что имели осциллограмму, соответствующую сдвигу фаз Dj = 60° или 300°. Если теперь подадим сигнал u2 на вход Y через фазовращатель, то фазовый сдвиг станет равен 150° или 30°. Как видно из рис. 12.3, при Dj = 60° осциллограмма из 1-го и 3-го квадрантов переместится в 3-й и 4-й, а при Dj = 300° останется в 1-м и 3-м квадрантах.
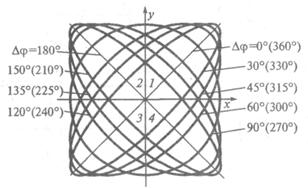
Рис. 3.8. Метод эллипса: осциллограммы при разных фазовых сдвигах
Погрешность измерения фазового сдвига между двумя синусоидальными сигналами методом эллипса зависит от точности измерения длин отрезков, входящих в выражение (12.9), и точности фокусировки луча на экране осциллографа. Эти причины оказывают тем большее влияние, чем ближе измеряемый сдвиг фаз к нулю или к 90°. Возможна также систематическая погрешность измерения из-за наличия различного фазового сдвига, создаваемого усилителями каналов вертикального и горизонтального отклонения лучей. Для ее устранения можно (перед началом измерений) подать один из исследуемых сигналов на вход Y осциллографа непосредственно, а на вход X — через регулируемый фазовращатель. Изменяя настройку фазовращателя, необходимо добиться появления на экране осциллографа наклонной прямой линии. Затем, сохраняя эту настройку, подать на вход фазовращателя второй сигнал (отключив предварительно первый) и провести требуемое измерение фазового сдвига сигналов.
Метод круговой развертки
Обеспечивает измерение фазового сдвига практически в пределах от 0 до 360°. Сущность метода поясняется схемами и эпюрами, приведенными на рис. 12.4, для случая измерения фазового сдвига между сигналами u1= Um1sinwt и u2 = Um2sinw(Dt-t).
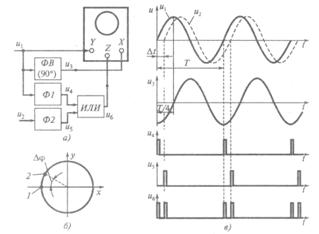
Рис. 3.9. Метод круговой развертки: а — схема измерения; б — осциллограмма;
в — эпюры сигналов
Генератор развертки осциллографа предварительно выключается и на входы Y и X подаются сигнал u1 и сигнал u3 (рис. 12.4, а), задержанный относительно u1 по фазе на 90° (с помощью дополнительного фазовращателя ФВ). При одинаковом отклонении электронного луча по горизонтали и вертикали на экране осциллографа будет наблюдаться осциллограмма, имеющая вид окружности (рис. 12.4, б).
Анализируемые сигналы u1 и u2 также поступают на входы идентичных формирователей Ф1 и Ф2, преобразующих синусоидальные колебания в последовательность коротких однополярных импульсов u4 и u5 (рис. 12.4, в). Передние фронты этих импульсов практически совпадают с моментом перехода синусоид через нулевое значение при их возрастании. Импульсные сигналы u4 и u5 объединяются с помощью логической схемы ИЛИ. Ее выходной импульсный сигнал u6 в виде двухимпульсных последовательностей подается на вход Z управления яркостью луча осциллографа. В результате на окружности (рис. 12.4, б) в точках 1 и 2 появляются отметки повышенной яркости.
Измерение фазового сдвига Dj между сигналами u1 и u2 выполняется так, как показано на рис. 12.4, б. Для измерения используется прозрачный транспортир, центр которого совмещается с центром окружности. Данный метод измерения основан на следующем. Полную окружность, которой соответствует угол 360°, луч описывает за время, равное периоду Т сигналов u1 и u2 , а дугу между точками 1 и 2, которой соответствует некоторый угол a, — за время задержки этих сигналов Dt = DjT / 3600. Отсюда следует, что угол a равен Dj.
На погрешность измерения влияют точности формирования окружности и определения ее центра, а также степень идентичности порога срабатывания формирователей и точность измерения угла Dj с помощью транспортира.
Компенсационный метод
Компенсационный метод основан на сравнении измеряемого фазового сдвига с известной величиной фазового сдвига, которую создает измерительный фазовращатель.
Структурная схема измерительной установки приведена на рис. 12.5. Она содержит измерительный фазовращатель ФВ и индикатор равенства фаз, в качестве которого использован осциллограф с отключенным генератором развертки. Сигнал u1 подается на вход Y осциллографа через ФВ, а сигнал u2 на вход X — непосредственно.
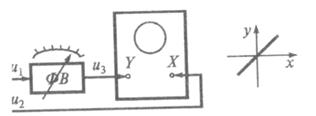
Рис. 3.10. К определению фазового сдвига компенсационным методом
Фазовый сдвиг Dj между двумя сигналами u1 и u2 определяется путем изменения фазы дополнительного сигнала из с помощью ФВ до момента появления на экране наклонной прямой линии (см. рис. 12.5), т.е. до момента равенства фаз сигналов u2 и u3. При этом искомый фазовый сдвиг Dj считывается по шкале ФВ. Для более точных измерений следует проверить и скомпенсировать возможное неравенство фазовых сдвигов, даваемых усилителями вертикального и горизонтального отклонения луча осциллографа. Это выполняется в порядке, изложенном выше, при рассмотрении метода эллипса.
Точность измерения компенсационным методом высокая. Погрешность измерения определяется в основном качеством градуировки шкалы фазовращателя и достигает (0,1...0,2)°.
3.3
Суть методов преобразования фазового сдвига в импульсы тока и дискретного или цифрового счета рассмотрим на примере реализации данных методов в средствах измерения разности фаз, которые согласно ГОСТ 15098-86 относятся к подгруппе Ф (Приборы для измерения разности фаз и группового времени запаздывания) и делятся на следующие виды:
Ф1 Установки или приборы для поверки измерителей разности фаз и группового времени запаздывания;
Ф2 Измерители разности фаз (приборы для измерения разности фаз между двумя сигналами одной частоты);
Ф4 Измерители группового времени запаздывания (приборы для измерения крутизны фазочастотных характеристик радиоустройств);
Ф5 Измерители разности фаз импульсные (приборы для измерения разности фаз между двумя импульсно-модулированными сигналами одной частоты).
Фазометр преобразования фазового сдвига в импульсы тока
Структурная схема устройства, реализующего метод преобразование фазового сдвига в импульсы тока, и поясняющие его эпюры, приведены на рис. 12.6.
В состав устройства входят преобразователь Dj ® Dt искомого фазового сдвига Dj в интервал времени Dt и измерительный прибор. Преобразователь имеет два одинаковых формирователя Ф1 и Ф2 и триггер Т.
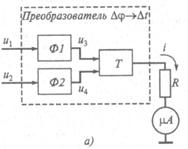

Рис. 3.11. Метод преобразования фазового сдвига в импульсы тока: а — схема устройства; б — эпюры сигналов
Синусоидальные сигналы u1 и u2 , имеющие некоторый фазовый сдвиг Dj, подаются на идентичные формирователи Ф1 и Ф2, преобразующие их в последовательности коротких импульсов u3 и u4 (рис. 12.6, б). Импульсы u3 запускают, а импульсы u4 сбрасывают триггер Т в исходное состояние. В результате на выходе триггера формируется периодическая последовательность импульсов напряжения, период повторения и длительность которых равны периоду Т и сдвигу во времени Dt исследуемых сигналов u1 и u3. Данные импульсы, поступая на резистор R, соединенный с измерительным прибором mА, преобразуются в последовательность импульсов тока i с аналогичными периодом и длительностью и некоторой амплитудой Im (рис. 12.6, б).
В качестве измерительного прибора часто используется микроамперметр магнитоэлектрической системы, реагирующий на среднее значение тока i за период его следования Т. Пусть SI и icp, — чувствительность прибора и среднее значение протекающего через него тока. Тогда показание прибора а определится по несложной формуле
 . (3.23)
. (3.23)
С учетом выражения (12.3) получим
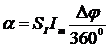 , (3.24)
, (3.24)
где Dj — искомый фазовый сдвиг.
Так как чувствительность SI, и амплитуда Im постоянны, то шкалу микроамперметра можно проградуировать непосредственно в градусах. Измеренное значение фазового сдвига является средним за время измерения.
Рассмотренное устройство является прямопоказывающим фазометром с равномерной шкалой. Диапазон его рабочих частот ограничен снизу инерционностью магнитоэлектрического прибора, а сверху — неидеальностью фронтов импульсов формирователей Ф1 и Ф2, влияющих на четкость работы триггера Т.
В качестве примера отметим параметры одного из фазометров, в основе работы которого используется изложенный метод. Диапазон рабочих частот фазометра от 20 Гц до 1 МГц; измеряемая разность фаз составляет ±180°, т.е. фазовый сдвиг измеряется в диапазоне (0...180)0. Погрешность измерений на частотах до 200 кГц равна (0,5±0,15 Dj)°, а на частотах до 1 МГц — (1 ±0,02 Dj)°.
Цифровой фазометр
Метод дискретного счета (более точное название — цифровой метод измерения фазового сдвига), используемый в цифровых фазометрах, включает две основные операции:
- преобразование фазового сдвига в соответствующий интервал времени;
- измерение интервала времени методом дискретного счета.
Рассмотрим реализацию метода дискретного счета в простейшем цифровом фазометре (рис. 12.7, а), в состав которого входят преобразователь Dj ® Dt искомого фазового сдвига Dj в интервал времени Dt, временной селектор ВС1, генератор счетных импульсов ГИ, счетчик СЧ и цифровое отсчетное устройство ЦОУ.
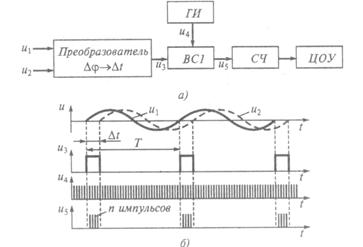
Рис. 3.12 Цифровой метод измерения фазового сдвига.
а — структурная схема; б — временные диаграммы
Устройство и принцип действия преобразователя Dj ® Dt рассмотрены выше. Временной селектор представляет собой ключевую логическую схему. Генератор счетных импульсов состоит из кварцевого генератора гармонических колебаний стабильной частоты и схемы формирования импульсов.
Цифровой фазометр работает следующим образом. Преобразователь Dj ® Dt из подаваемых на его входы синусоидальных сигналов u1 и u2, имеющих фазовый сдвиг Dj, формирует последовательность прямоугольных импульсов u3 (рис. 12.7, б), имеющих длительность Dt и период повторения Т, равные соответственно сдвигу во времени и периоду сигналов u1 и u2.
Импульсы u3, а также счетные импульсы u4 вырабатываемые генератором ГИ, подаются на входы временного селектора ВС1. Данный селектор открывается на время, равное длительности Dt импульсов u3, и в течение этого времени пропускает на выход импульсы генератора u4. При этом на выходе селектора ВС1 формируются пакеты импульсов u5, следующие с периодом Т.
За один период повторения Т сигналов u1 и u2 на счетчик СЧ с выхода селектора поступает количество импульсов, содержащееся в одном пакете и равное
n =Dt/T0, (3.25)
где T0 — период следования счетных импульсов генератора ГИ.
Подставляя в (12.12) соотношение для Dt, из (12.3) находим выражение для измеряемого фазового сдвига сигналов u1 и u2:
Dj = n 3600 T0 / T. (3.26)
Кодовый сигнал со счетчика, пропорциональный фазовому сдвигу Dj, подается на цифровое отсчетное устройство, показания которого выдаются в градусах.
Погрешность данного цифрового фазометра определяется погрешностью дискретности и аппаратурной погрешностью. Погрешность дискретности связана с тем, что интервал времени Dt можно измерить с точностью до одного периода счетных импульсов. Аппаратурная погрешность определяется нестабильностью времени срабатывания триггера преобразователя Dj ® Dt.
Для уменьшения погрешностей используют фазометры среднего значения, результат измерения которых является средним значением измеряемого фазового сдвига за большое число периодов Т.
|
| Профессор кафедры
А. Елисеев
|






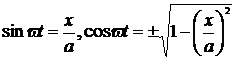 , (3.19)
, (3.19) , (3.21)
, (3.21)
 , (3.22)
, (3.22)




 . (3.23)
. (3.23)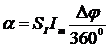 , (3.24)
, (3.24)



