Вопрос 15. Дифференциал функции двух переменных. Геометрический смысл дифференциала функции двух переменных. - главная линейная часть приращения функции.

1) Действительная функция y = f{x)действительного переменного наз. дифференцируемой в точке х, если она определена в нек-рой окрестности этой точки и если существует такое число А, что приращение

(при условии, что точка х+Ах лежит в упомянутой окрестности) может быть представлено в виде

где 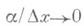при При 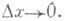этом А Ах обозначается через dy и наз. дифференциалом функции f(х)в точке х. Д. dy при фиксированном хпропорционален Ах, т. е. является линейной функцией от D х. Дополнительный член a при является, в силу определения, бесконечно малой более высокого порядка по сравнению с D х (и по сравнению с dy, если ). Именно в этом смысле Д. и наз. главной частью приращения функции.

Для функции, дифференцируемой в точке х, 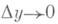при 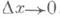, т. е. функция, дифференцируемая в некоторой точке, непрерывна в ней. Функция f(x)дифференцируема в точке хв том и только в том случае, если она имеет в этой точке конечную производную

при этом

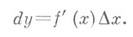
Существуют непрерывные, но не дифференцируемые функции.

Кроме обозначения dy используется обозначение df (x);тогда предыдущее равенство принимает вид

Приращение аргумента Ах обозначается также через dx и наз. дифференциалом независимого переменного. Поэтому можно писать

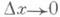Отсюда f(x) =dyldx, т. е. производная равна отношению Д. dy и dx. Если А=0, то при Dx->0, т. е. Ау и dy при являются в случае А неравно 0 эквивалентными бесконечно малыми; этим, рав, но как и простой структурой Д. (линейностью по Ах), часто пользуются в приближенных вычислениях, полагая D y=dy при малых D х. Если хотят, напр., вычислить f(x+ Dx), зная f{x)(Dxмало), то полагают

Конечно, такое рассуждение имеет ценность, если можно оценить соответствующую погрешность.

Геометр и чес к ое истолкование Д. Уравнение касательной к графику.функции y=f (x)в точке М(х ₀, у ₀). имеет вид y-y₀=f ' (х ₀)(х-х ₀). Если положить x=x₀+ D х, то y-y₀ =f'(х ₀)D х. Правая часть есть значение Д. функции f(x)в точке х ₀, отвечающее рассматриваемому значению Ах. Таким образом, Д. совпадает с соответствующим, приращением ординаты касательной к кривой y-f (x)(см. отрезок NT на рис. 1).

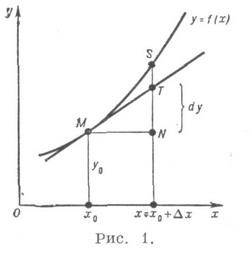
При этом a = Dу- dy, т. е. значение |a| совпадает с длиной отрезка TS.

2) Определение дифференцируемости и Д. естественным образом обобщается на действительные функции от пдействительных переменных. Напр., в случ. п=2 действительная функция z=f(x, у)наз. дифференцируемой в точке (х, у)по совокупности переменных хи у, если она определена в нек-рой окрестности этой точки и ее полное приращение

может быть представлено в виде

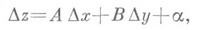
где Аи В- некоторые числа, 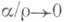при r= предполагается, что точка (х+ D х, у+ Dy). принадлежит упомянутой окрестности (см. рис. 2) При этом вводится обозначение 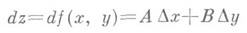и dz наз. полным дифференциалом, или просто дифференциалом, функции f(x,у). в точке (х, у)(иногда с добавлением: "по совокупности переменных хи у"). Для фиксированной точки (х, у)Д. dz есть линейная функция от Ах и Ау;разность а= Az- dz есть бесконечно малая более высокого порядка по сравнению с р. В этом смысле dz есть главная линейная часть приращения Az.

Если f(x, у)дифференцируема в точке (х, у), то oн непрерывна в этой точке и имеет в ней конечные частные производные

Таким образом

Приращения Ах и Ау независимых переменных, как и в случае одного переменного, обозначаются dx и dу По этой причине можно написать

Существование конечных частных производных, во обще говоря, не влечет дифференцируемости функции (даже если предполагать заранее ее непрерывность) здесь нарушается аналогия с функциями одного переменного.

Если функция f(x, у)имеет в точке (х, у)частную производную по х, то произведение f_x (x, y) dx наз. частным дифференциалом по х;аналогично, f'_y (x, y) dy есть частный Д. по у. Если функция дифференцируема, то ее полный Д. равен сумме частных Д. Геометрически полный Д. df (x₀, у ₀)есть приращение аппликаты касательной плоскости поверхности z-f (x, у)в точке (х ₀, у ₀, z₀), где z₀=f(z₀, у ₀)(см. рис. 3).

Достаточный признак дифференцируемости функции: если в некоторой окрестности точки (x₀, y₀) функция f(x, у) име ет частную производную f'_x, непрерывную в точке (х ₀, у₀), и, кроме того, имеет в точке (х ₀, у ₀)частную производную f'_y, то f(x, у)дифференцируема в этой точке Если функция f(x, у)дифференцируема в каждо точке открытой области D, то в любой точке этой области причем (х, y) = f_x (x, у), В (х, y) = f'_y (x, у). Если при этом существуют непрерывные в Dчастные производные А' _у и В' _х, то всюду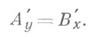

Это показывает, в частности, что не всякое выражение с непрерывными А и В (вобласти D)является в этой области полным Д. нек-рой функции двух переменных. В этом состоит еще одно нарушение аналогии с функциями одного переменного, где любое выражение A(x) dx с непрерывной в нек-ром промежутке функцией (х). служит Д. для нек-рой функции.

Выражение Adx+Bdy является полным Д. нек-рой функции z=f (x, у), в односвязной открытой области D, если (х, у)и В(х, у)непрерывны в этой области и удовлетворяют условию А' =В' _Х и при этом а) А' _y и В' _х непрерывны или б) (х, у) и В (х, у) дифференцируемы по совокупности переменных хи увсюду в D(см. [7], [8]).

О Д. действительных функций одного или нескольких действительных переменных и о Д. высших порядков см. также Дифференциальное исчисление.

3) Пусть функция f(x)определена на нек-ром множестве Едействительных чисел, х- предельная точка этого множества, Dy=АDx+a, где

при ; тогда функция f(x)наз. дифференцируемой по множеству Ев точке х, a dy=A D х наз. ее дифференциалом" по множеству Еточке х. Это есть обобщение Д. действительной функции одного действительного переменного. Разновидностями этого обобщения являются Д. в концах промежутка, на котором определена функция, и аппроксимативный Д. (см. Аппроксимативная дифференцируемоетъ).

Подобным же образом вводится Д. по множеству для действительных функций многих действительных переменных.

4) Все эти определения дифференцируемости и Д. почти без изменений распространяются соответственно на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе они распространяются на функции точки абстрактного пространства. Можно говорить о дифференцируемости и Д. функции множества по отношению к нек-рой мере.

.