16.1. Первоначальные сведения. В дальнейшем при рассмотрении электромагнитных полей в областях с круговой симметрией встретится обыкновенное дифференциальное уравнение вида
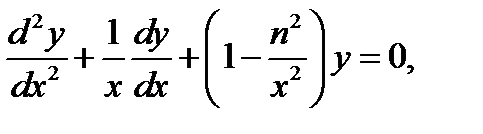 (16.1)
(16.1)
которое называется уравнением цилиндрических функций, или уравнением Бесселя n -го порядка. Ниже сообщаются некоторые сведения о его решениях, цилиндрических функциях. Поскольку вы достаточно знакомы с тригонометрическими и экспоненциальными функциями, являющимися решениями уравнения
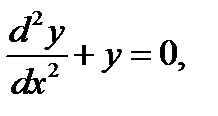 (16.2)
(16.2)
то начнём с замечания, что это уравнение при некоторых ограничениях можно рассматривать как предельную форму уравнения Бесселя (16.1) при х ® ∞. Ввиду указанного обстоятельства, между различными решениями обоих уравнений существует соответствие; это поможет понять роль цилиндрических функций в разных задачах, а также их взаимные соотношения. Частным решениям уравнения (16.2) cosx, sinx соответствуют следующие частные решения уравнения (16.1):
Jn (х)- функция Бесселя n -го порядка,
Nn (x) -.функция Неймана n -го порядка.
Точно так же частным решениям (16.2) ejx, е-ix соответствуют частные решения уравнения (16.1):
H( 1)n(х) - функция Ханкеля 1-го рода п-го порядка,
Н(2)n (х) - функция Ханкеля 2-го рода п-го порядка.
На рис. 16.1 приведены графики некоторых из цилиндрических функций. Подобно тому, как 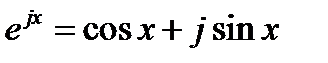 ,
, 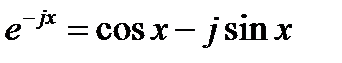 имеют место соотношения
имеют место соотношения
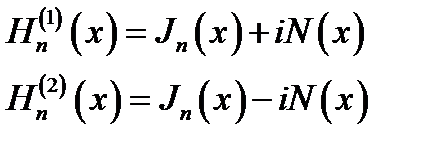 (16.3)
(16.3)
Цилиндрические функции не являются периодическими (как, например, тригонометрические функции вещественного аргумента), однако это «осциллирующие», колеблющиеся функции. Функции Jn (x)и Nn (x)с возрастанием положительного х принимают значения, колеблющиеся около нуля с монотонно убывающей амплитудой. Их графики создают впечатление деформированных тригонометрических кривых.
Полезно помнить, что
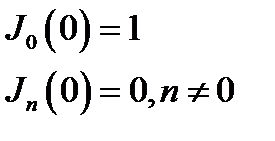 , (16.4)
, (16.4)
и 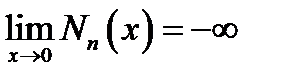 (16.5)
(16.5)
Подобно общим решениям у = Acosx + Bsinx и y = Pe-jx + Qejx, уравнения (16.2) имеют общие решения уравнения Бесселя (16.1) в виде:
y = AJn(x) + BNn(x) (16.6а)
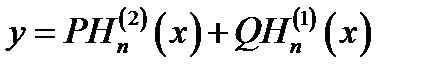 . (16.б)
. (16.б)
Обычно требуется, чтобы решение задачи удовлетворяло условию ограниченности | у | < ∞. Соответственно этому, если в рассмотрение входит точка х = 0, то общее решение уравнения Бесселя (16.1) ввиду (16.5) имеет вид:
y = AJn (x).(16.7)
Действительно, единственная возможность получения ограниченного решения,на отрезке, включающем нуль, состоит в том, что неопределённый коэффициент В в (16.6а) полагается равным нулю.
16.2. Асимптотические представления. При неограниченно возрастающем аргументе Jn (x)и Nn (x)переходят в тригонометрические функции, 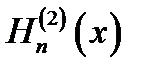 и
и 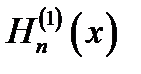 - в экспоненциальные:
- в экспоненциальные:
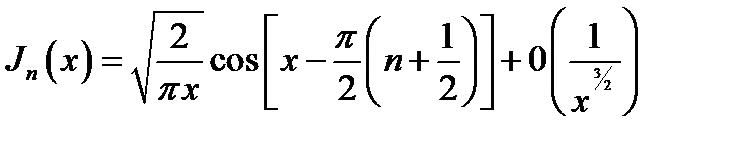 (16.8)
(16.8)
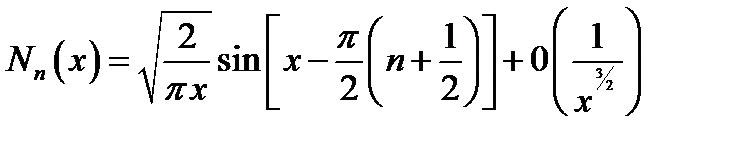 (16.9)
(16.9)
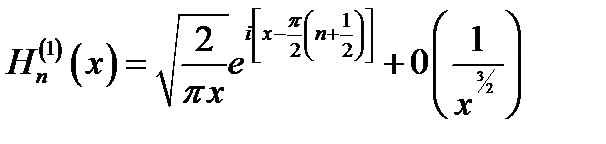 (16.10)
(16.10)
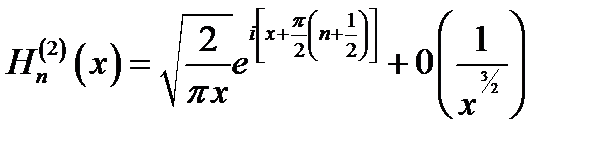 (16.11)
(16.11)
Напомним (п. 9.3), что употребленный здесь символ 0 (...) означает величину, убывающую при х → ∞ как функция, заключённая в скобки (в данном случае 1/х3/2).
Весьма существенно следующее. Пусть х = kz,и решение уравнения Бесселя (16.1) должно иметь характер комплексной амплитуды волны, распространяющейся в сторону возрастания z. Тогда оно выражается функцией Ханкеля второго рода, т. е. получается из (16.6 б) при Q = 0:
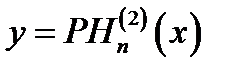 (16.12)
(16.12)
Это вытекает из приведенных асимптотических представлений (16.10), (16.11).
16.3. Степенные ряды; представления функций малого аргумента. Функции. Бесселя представляются степенными рядами вида:
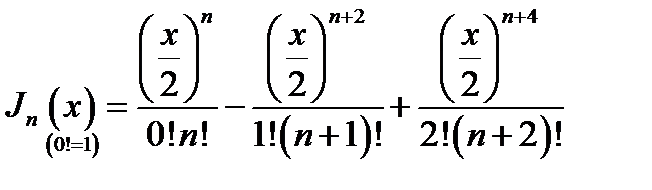 (16.13)
(16.13)
В частности,
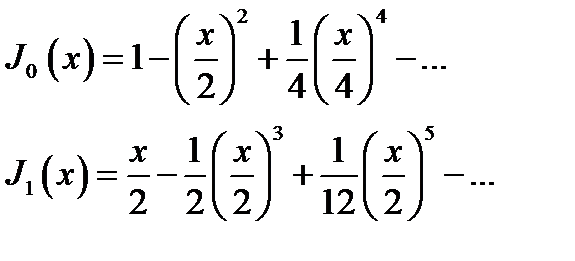 (16.13а)
(16.13а)
Поэтому при |х | << 1
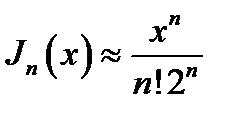 (16.14)
(16.14)
В частности,
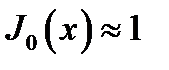 и
и 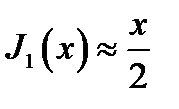 (16.14а)
(16.14а)
Ввиду громоздкости ряд для функций Неймана мы не приводим. При |х|<< 1 эти функции представляются в виде:
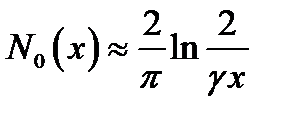 и
и 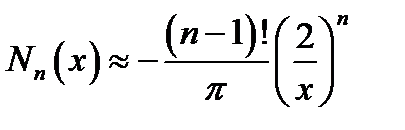 , (16.15)
, (16.15)
(γ = 1,781…).
16.4. Функциональные соотношения. Запишем ещё ряд употребительных формул, используя символ Zn (x)для обозначения произвольной цилиндрической функции (формулы верны при подстановке в качестве Zn (x)функций Бесселя, Неймана или Ханкеля).
Для натурального п
Z-n (x) = (-1 )nZn (x).(16.16)
В частности,
Z-1 (x) = - Zt(x). (16.16a)
В справедливости (16.16) для функций Бесселя нетрудно убедиться на основании ряда (16.13).
При дифференцировании цилиндрических функций пользуются соотношениями:
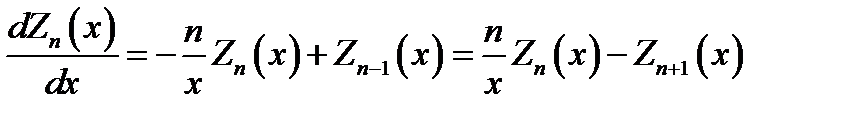 (16.17)
(16.17)
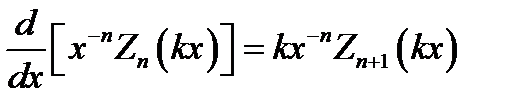 , (16.18)
, (16.18)
а также 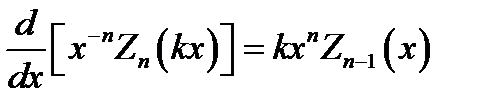 . (16.19)
. (16.19)
Из (16.17) следует:
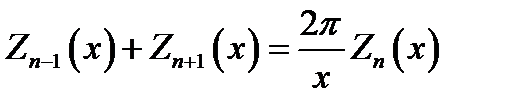 . (16.20)
. (16.20)
Для n = 0 и n = 1 из (16.17) получаем:
Z0(x) = - Zt (x) и 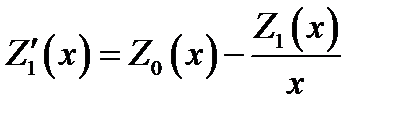 . (16:21)
. (16:21)
Запишем также некоторые неопределённые интегралы, содержащие цилиндрические функции:
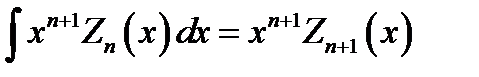 ; (16.22)
; (16.22)
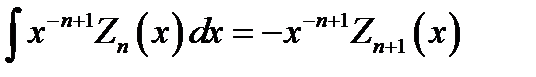 (16.23)
(16.23)
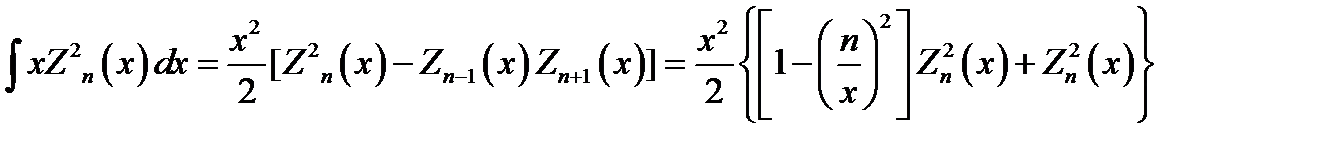 ; (16.24)
; (16.24)
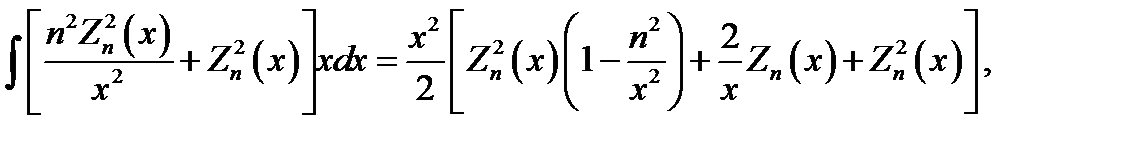 (16.25)
(16.25)
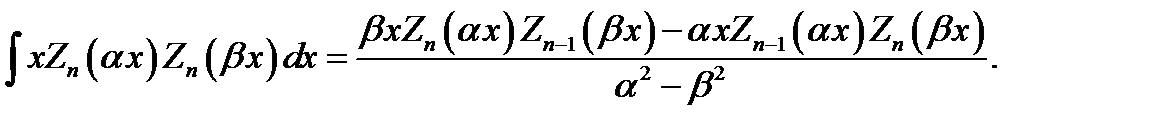
Эти формулы нетрудно проверить, используя приведенные ранее дифференциальные соотношения.
16.5. Интегральное представление функций Бесселя. Функции Бесселя Jn(x) при целом п могут быть представлены в виде:
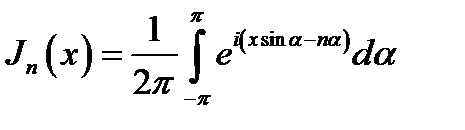 (16.27)
(16.27)
Это интегральное представление в дальнейшем будет играть важную роль. Мы используем его также для частичного обоснования ранее приведенных соотношений.
Убедимся сначала, что (16.27), действительно, выражает решение уравнения Бесселя (16.1). С этой целью произведем в (16.27) интегрирование по частям и получим:
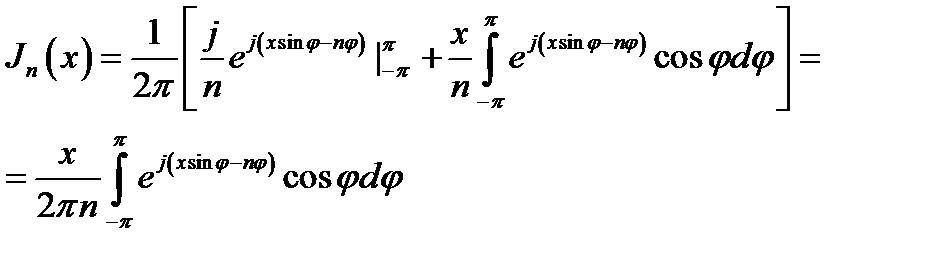 (16.28)
(16.28)
(первый член в квадратных скобках уничтожается).
Далее вычислим производную J'n(x) и также преобразуем полученное выражение путём интегрирования его по частям:
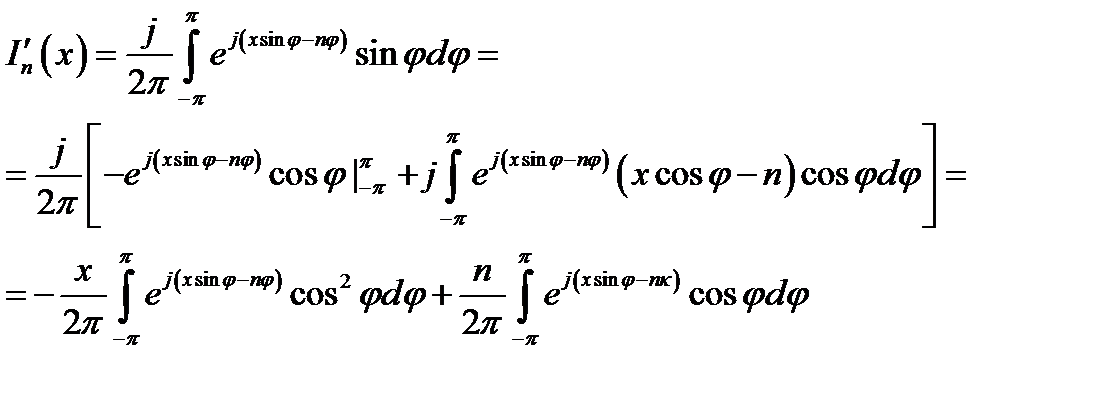 (16.29)
(16.29)
Вторая производная J"n(x) имеет вид:
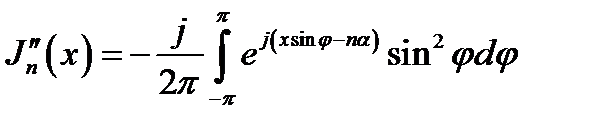 . (16.30)
. (16.30)
Внося (16.28), (16.29) и (16.30) в уравнение (16.1), имеем тождество:
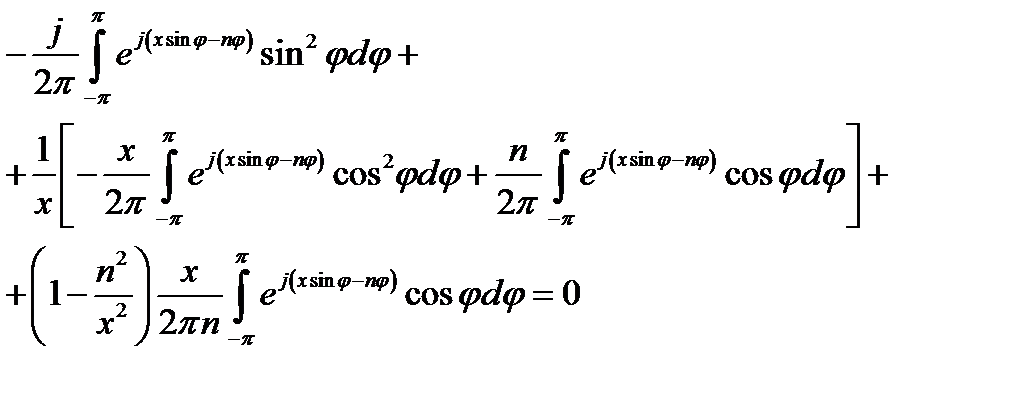 ,
,
в чём немедленно убеждаемся после элементарных преобразований с привлечением (16.27) и (16.28).
Используя интегральное представление (16.27), нетрудно проверить приведенные в п. 4 дифференциальные соотношения. Покажем это на примере формулы (16.17). Согласно (16.27)
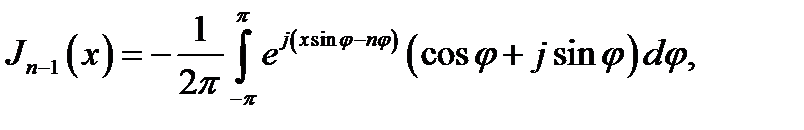
т. е. можно написать:
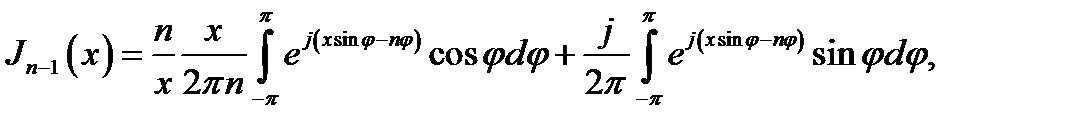
что с учётом (16.28) и (16.29) дает:
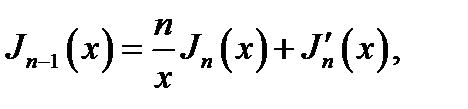
а это совпадает с первым из равенств (16.17) при Zn (х) =Jn (x).
16.6. Разложение по функциям Бесселя. Далее начнём с рассмотрения ряда Фурье некоторой функции f (φ), определённой на отрезке 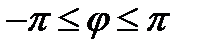 , по функциям ejna. Вы можете получить этот ряд, заменив в (12.22) V (t)на f (φ) и положив ω = 1. Таким образом, имеем:
, по функциям ejna. Вы можете получить этот ряд, заменив в (12.22) V (t)на f (φ) и положив ω = 1. Таким образом, имеем:
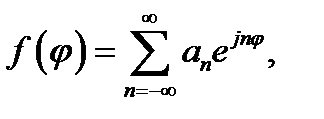 . (16.31а)
. (16.31а)
где
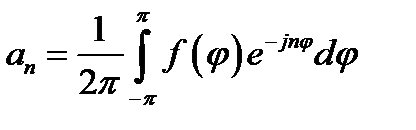 (16.31б)
(16.31б)
Особый интерес для нас представляет функция f (φ) = ejxsinφ. Внося её в (16.316) и учитывая интегральное представление (16.27), имеем: an= Jn(x). Ряд Фурье (16.31а) функции ejxsinφ следовательно, имеет вид:
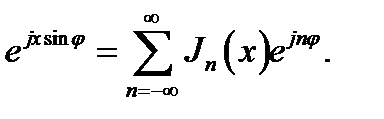 (16.32)
(16.32)
Получено разложение, содержащее функции Бесселя всех целых порядков.
Выведем ещё важную модификацию разложения (16.32). Заменяя слева и справа от знака равенства φ на 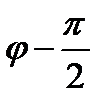 , находим:
, находим:
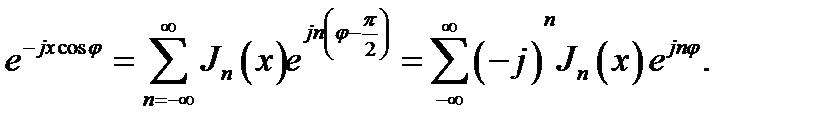 (16.33)
(16.33)
Этот результат может иметь, например, следующее применение. Пусть вдоль оси z распространяется плоская однородная волна, комплексная амплитуда которой изменяется, как e-jkz. Введём цилиндрическую систему координат (рис. 16.2), в которой z = rcosφ, так что e-jkz = e-jkrcosφ. Поэтому, делая в (16.33) замену х → kr находим:
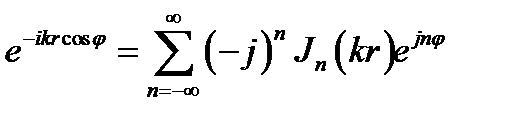 . (16.34)
. (16.34)
Это разложение плоской однородной волны по гармоникам Jn(kr)eina, которые можно истолковать как бегущие по азимуту φ (по часовой стрелке или против неё в зависимости от знака п)плоские неоднородные волны.
Разложение (16.32) можно применить для получения степенного ряда (16.13). Обозначив e-jα = p, перепишем (16.32) в виде:
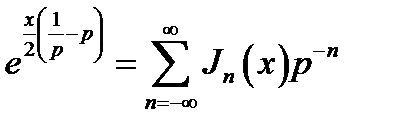 (16.35)
(16.35)
Левую часть будем рассматривать как произведение функций 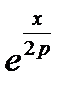 и
и 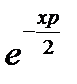 , которые можно разложить в степенные ряды:
, которые можно разложить в степенные ряды:

и
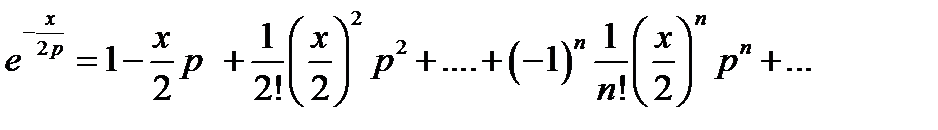
Перемножая ряды и выделяя коэффициенты при степенях р-k в получаемом произведении, приравняем их соответствующим коэффициентам в правой части (16.35), т. е. функциям Бесселя J k(х); это и должно привести к (16.13). Например, для получения разложения J0 (х)надо перемножить лишь члены рядов с одинаковыми номерами:
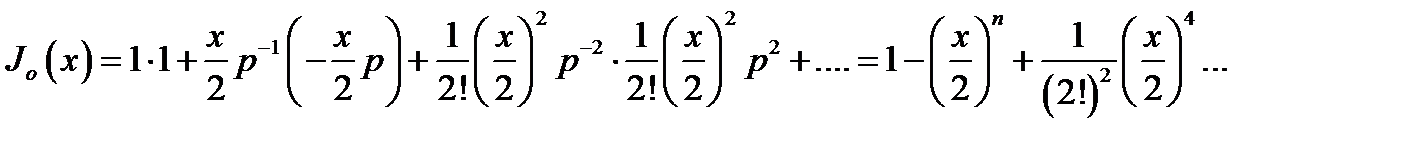
Как видно, результат совпадает с соответствующим рядом (16.13а).
Для нахождения ряда (16.13) при любом порядке функции Бесселя п >0 надо каждый (m + n) -ый член разложения 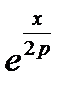 умножить на m -ый член разложения
умножить на m -ый член разложения 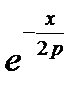 просуммировать от т = 0. Это даёт:
просуммировать от т = 0. Это даёт:
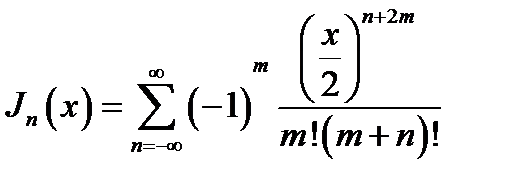 (16.36)
(16.36)
Мы получили краткую запись ряда (16.13).
17. Решение однородного уравнения Гельмгольца
методом разделения переменных
17.1. Декартовы координаты. Однородное уравнение Гельмгольца будет встречаться в дальнейшем при постановке разных граничных задач. Случай декартовых координат является простейшим, и поэтому именно с него начинается изложение. Уравнение Гельмгольца
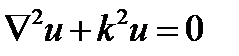 (17.1)
(17.1)
при использовании декартовой системы координат (х, у, z)принимает вид:
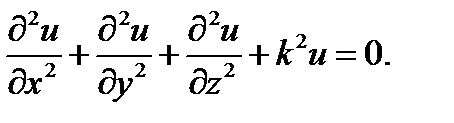 (17.2)
(17.2)
Рассмотрим получение его решений методом разделения переменных (п.11.1).
Ожидаемое решение и = и (х, у, z)представляется в виде произведения
и(х, у, z) = X(x)Y(y)Z(z), (17.3)
где Х (х), Y (y)и Z (z) - функции координат х, у, и z соответственно. Подставим представление (17.3) в уравнение (17.2) и разделим все члены на u = XYZ. Это дает:
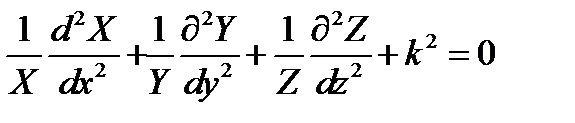 . (17.4)
. (17.4)
Как видно, первые три члена - функции разных аргументов, а третий постоянен. Это дает основание (§11 п. 1) положить каждую из указанных функций константе; назвав введённые константы 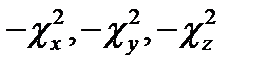 ,получаем три обыкновенных дифференциальных уравнения:
,получаем три обыкновенных дифференциальных уравнения:
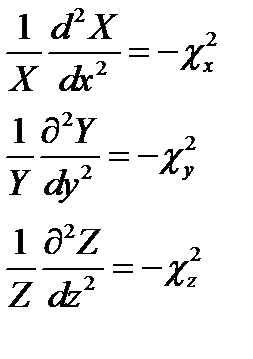 , причём
, причём 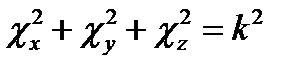 (17.5)
(17.5)
Это уже много раз встречавшиеся уравнения типа (7.7) с решениями (7.8). Таким образом, сразу можно выразить решение (17.3) уравнения (17.2):
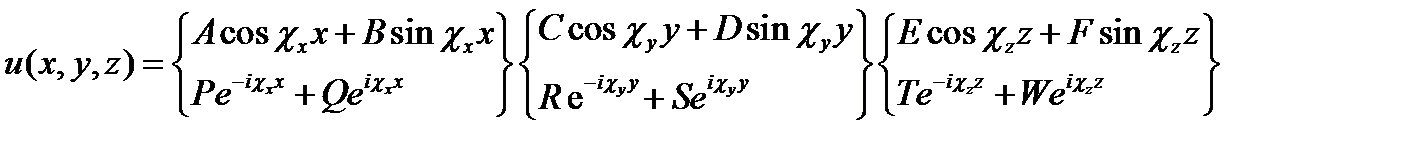 (17.6)
(17.6)
Данная символическая запись означает, что каждый из сомножителей решения (X, Y и Z) можно брать как в форме верхней строчки, так и в форме нижней. Очевидно, что записанная функция (17.6) выражает решение уравнения (17.2) при любых постоянных коэффициентах А, В,..., Т, W и любых «постоянных разделения» 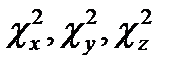 , подчинённых равенству в нижней строке.
, подчинённых равенству в нижней строке.
В случае двумерного уравнения Гельмгольца
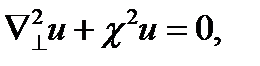 (17.7)
(17.7)
записываемого в декартовых координатах как
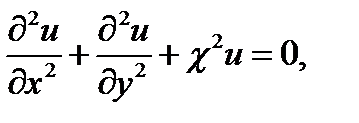 (17.8)
(17.8)
имеем:
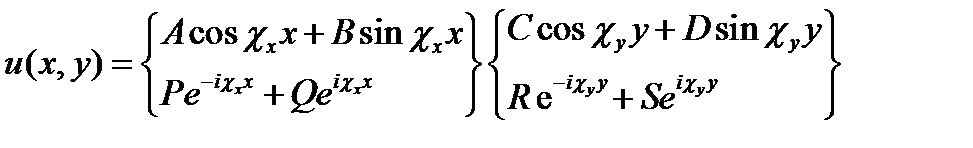 (17.9)
(17.9)
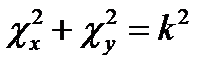
17.2. Цилиндрические координаты.В цилиндрической системе координат (r, φ, z) согласно (6.17) уравнение (17.1) примет вид:
 (17.10)
(17.10)
Полагая
и (r, φ, z) = U (r) W (φ) Z (z) (17.11)
где U (r), W (φ)и Z (z) - функции координат r, φ и z соответственно. В результате подстановки (17.11) в (17.10) и деления на и = UWZ получаем:
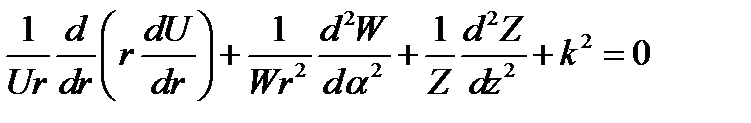 (17.12)
(17.12)
Третий член есть функция только координаты z и, таким образом, независим от предыдущих. Это дает основание (§ 11 п. 1) положить его равным некоторой постоянной; последнюю обозначим - χ2z. Оставшиеся слева члены в сумме также равны постоянной величине, а именно 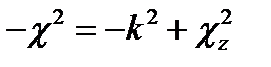 . Поэтому имеем следующие уравнения:
. Поэтому имеем следующие уравнения:
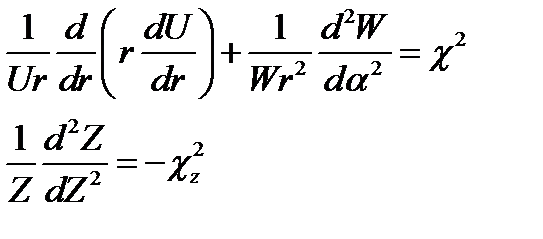
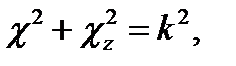 (17.13)
(17.13)
эквивалентные вместе первоначальному уравнению (17.12).
Далее произведём операцию разделения переменных в первом из уравнений (17.13), которое после умножения всех членов на r2 принимает форму:
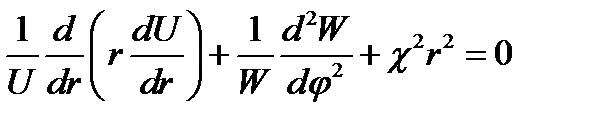 .
.
Второй член (функция φ) не зависит от первого и третьего (функций r). Поскольку сумма всех членов - нуль, введём, как делалось в п. 11, постоянные п2 и - п2, которые в сумме равны нулю, и получим:
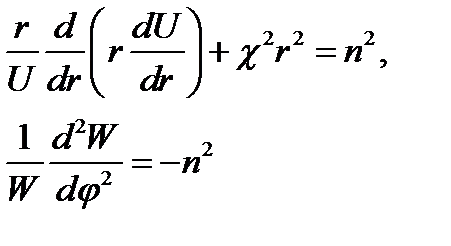 (17.14)
(17.14)
Легко убедиться, что в первой строчке (17.14) мы имеем не что иное, как уравнение Бесселя относительно U как функции аргумента χr. Действительно, после дифференцирования по r и умножения всех слагаемых на U /χ2 имеем:
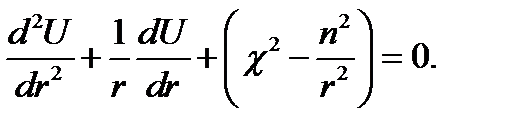 (17.15)
(17.15)
Оно совпадает с уравнением (16.1) при замене х на χr.
Итак, объединяя результаты (17.13) и (17.14) с учётом (17.15), получаем совокупность следующих обыкновенных дифференциальных уравнений, эквивалентную уравнению Гельмгольца (17.10):
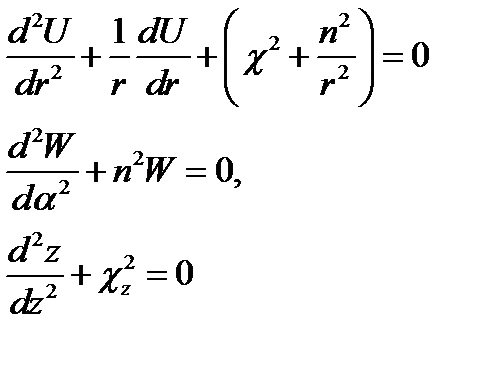
 (17.16)
(17.16)
Общие решения их известны, причём каждое можно записать в двух формах: с использованием функций Бесселя и Неймана или Ханкеля для первого уравнения согласно (16.6 а, б) и с использованием функций тригонометрических или экспоненциальных - для двух последних уравнений. Таким образом, находим следующее выражение и = UWZ:
u(r, φ,z) =
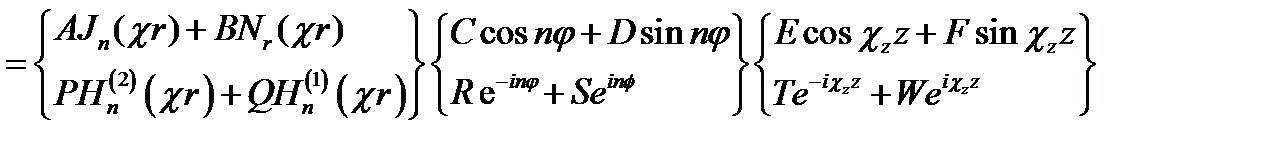 17.17
17.17
Форма записи имеет тот же смысл, что и в (17.6); аналогично также значение входящих в выражение постоянных.
Обычно область, в которой ищется решение, не ограничена по углу φ. В этом случае М(r, φ, z) и М(r, φ + 2π, z) - это одна и та же точка наблюдения, а следовательно, u (r, φ, z) и и (r, φ + 2π, z) выражают решение в одной и той же точке, т. е. должно быть:
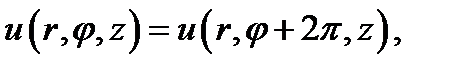 , (17.18)
, (17.18)
что возможно только при целом п (или равном нулю): п = 0, ±1, ±2,....
При отсутствии зависимости по z уравнение Гельмгольца (17.1) записывается в форме (17.7), т. е. в цилиндрических координатах:
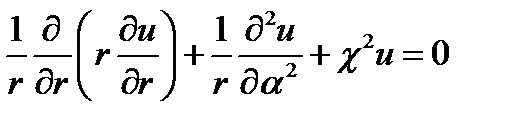 . (17.19)
. (17.19)
Его решение имеет вид:
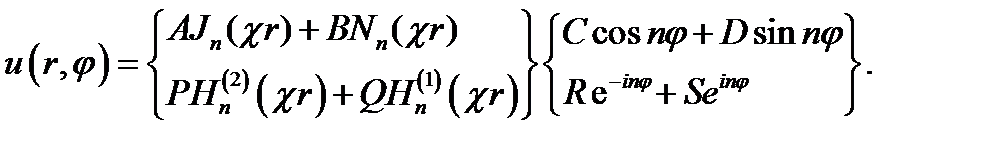 (17.20)
(17.20)
Выбор того или иного варианта решения определяется граничными условиями конкретной электродинамической задачи.



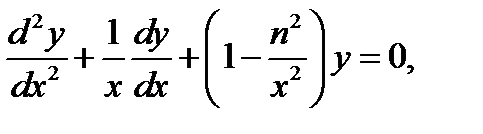 (16.1)
(16.1)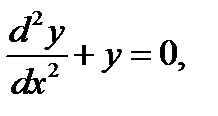 (16.2)
(16.2)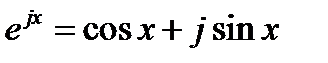 ,
, 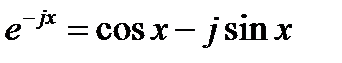 имеют место соотношения
имеют место соотношения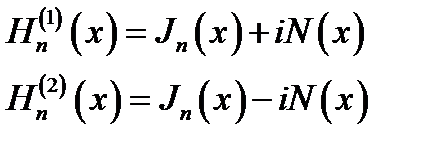 (16.3)
(16.3)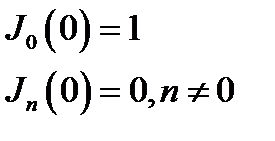 , (16.4)
, (16.4)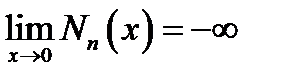 (16.5)
(16.5)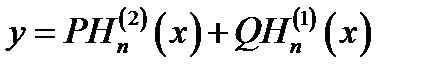 . (16.б)
. (16.б)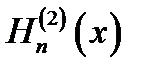 и
и 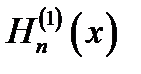 - в экспоненциальные:
- в экспоненциальные: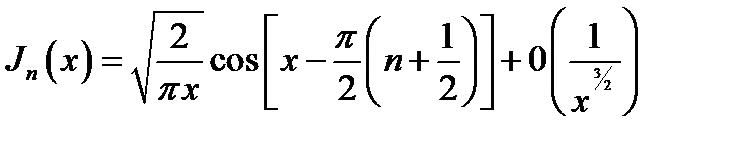 (16.8)
(16.8)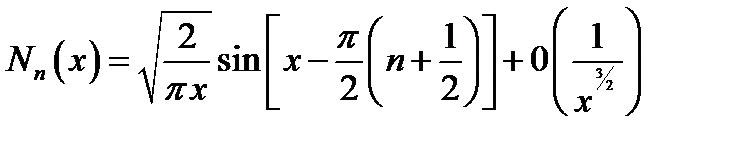 (16.9)
(16.9)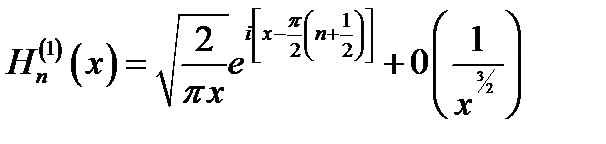 (16.10)
(16.10)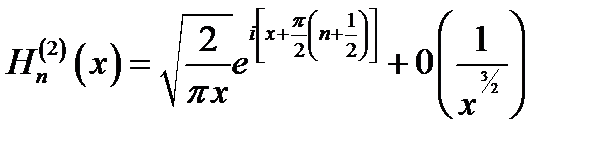 (16.11)
(16.11)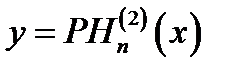 (16.12)
(16.12)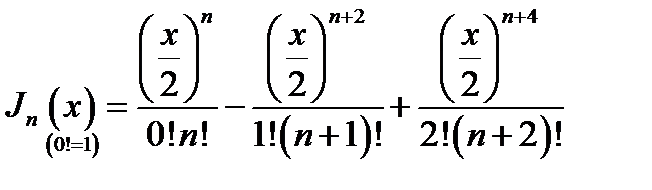 (16.13)
(16.13)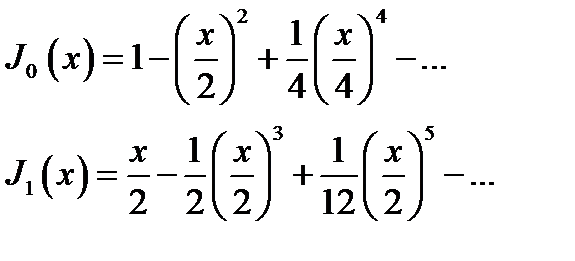 (16.13а)
(16.13а)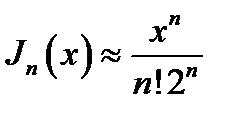 (16.14)
(16.14)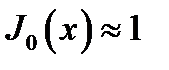 и
и 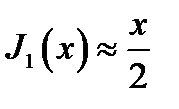 (16.14а)
(16.14а)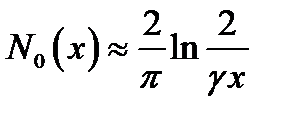 и
и 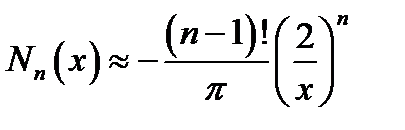 , (16.15)
, (16.15)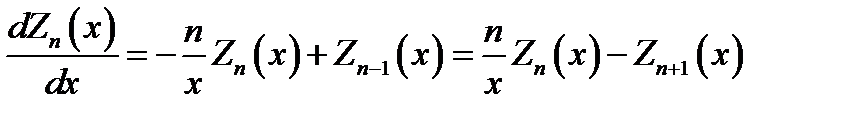 (16.17)
(16.17)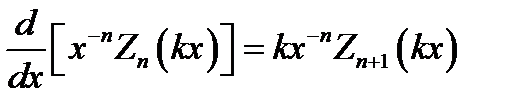 , (16.18)
, (16.18)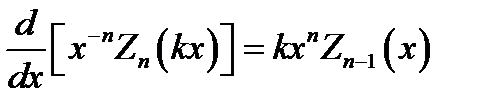 . (16.19)
. (16.19)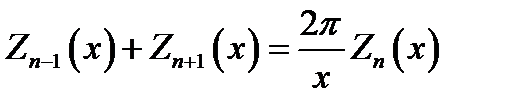 . (16.20)
. (16.20)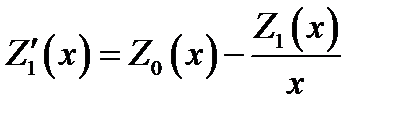 . (16:21)
. (16:21)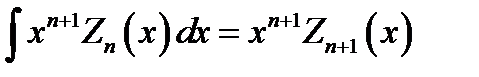 ; (16.22)
; (16.22)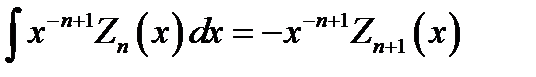 (16.23)
(16.23)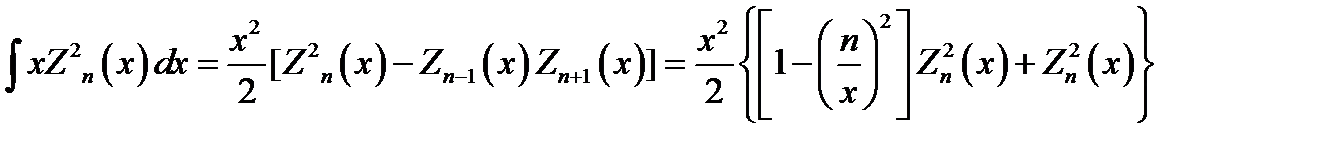 ; (16.24)
; (16.24)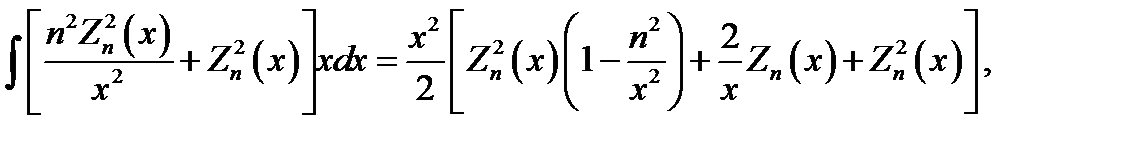 (16.25)
(16.25)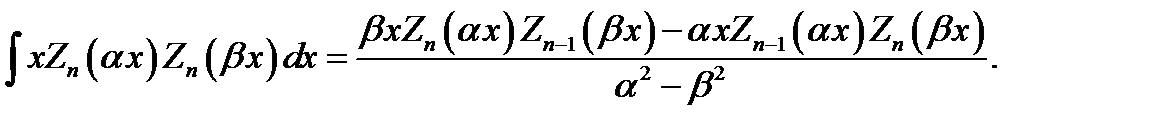
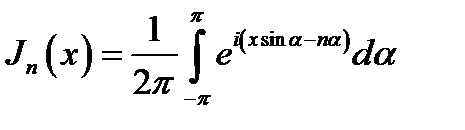 (16.27)
(16.27)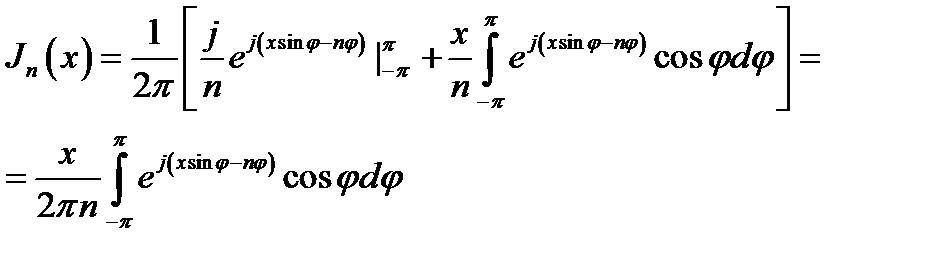 (16.28)
(16.28)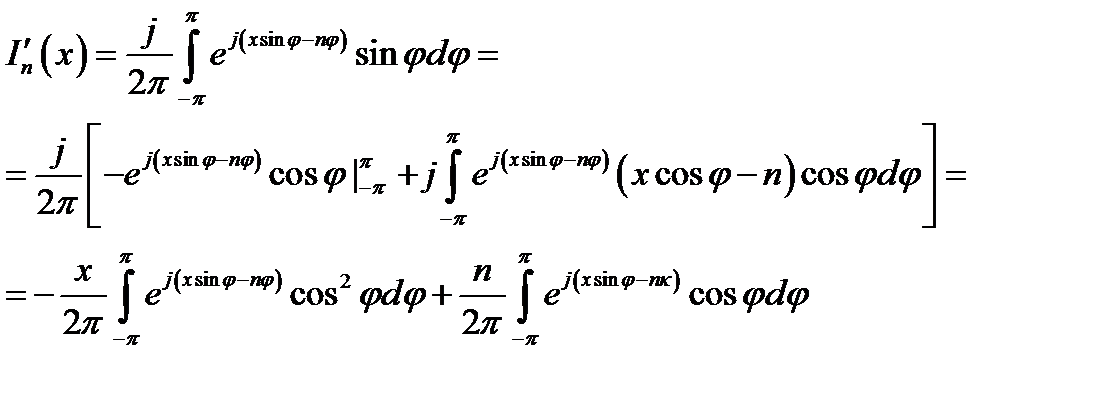 (16.29)
(16.29)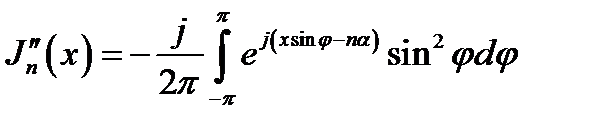 . (16.30)
. (16.30)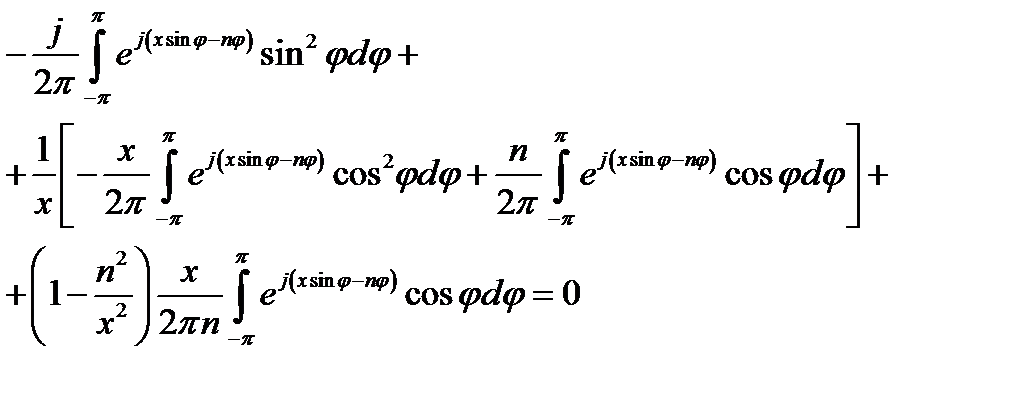 ,
,
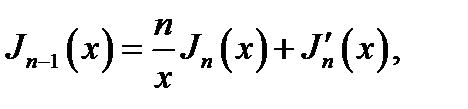
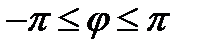 , по функциям ejna. Вы можете получить этот ряд, заменив в (12.22) V (t)на f (φ) и положив ω = 1. Таким образом, имеем:
, по функциям ejna. Вы можете получить этот ряд, заменив в (12.22) V (t)на f (φ) и положив ω = 1. Таким образом, имеем: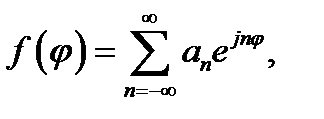 . (16.31а)
. (16.31а)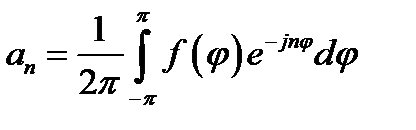 (16.31б)
(16.31б)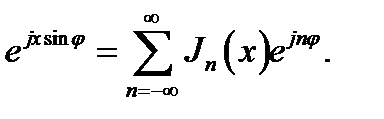 (16.32)
(16.32)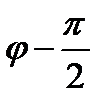 , находим:
, находим: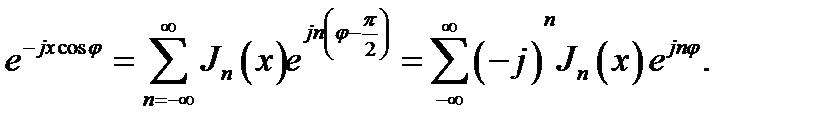 (16.33)
(16.33)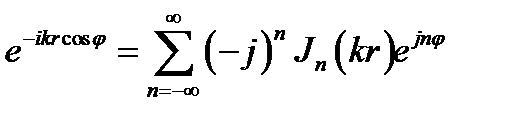 . (16.34)
. (16.34)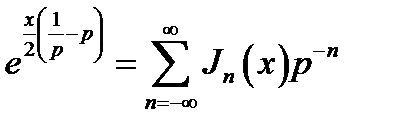 (16.35)
(16.35)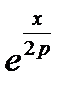 и
и 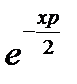 , которые можно разложить в степенные ряды:
, которые можно разложить в степенные ряды:
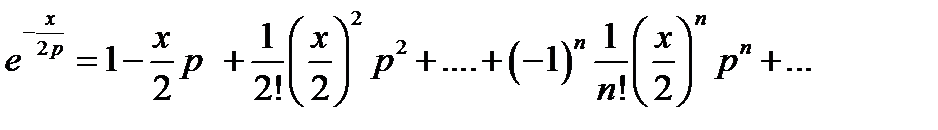
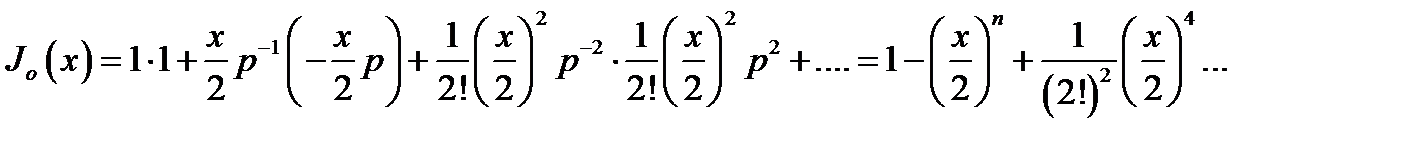
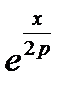 умножить на m -ый член разложения
умножить на m -ый член разложения 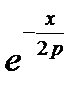 просуммировать от т = 0. Это даёт:
просуммировать от т = 0. Это даёт: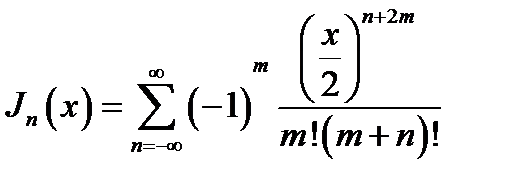 (16.36)
(16.36)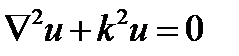 (17.1)
(17.1)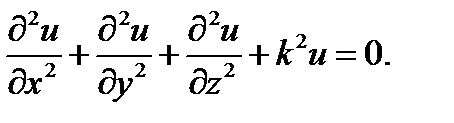 (17.2)
(17.2)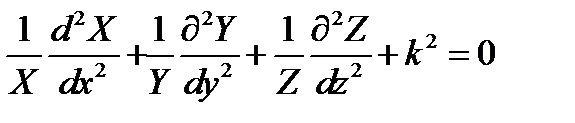 . (17.4)
. (17.4)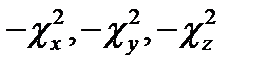 ,получаем три обыкновенных дифференциальных уравнения:
,получаем три обыкновенных дифференциальных уравнения: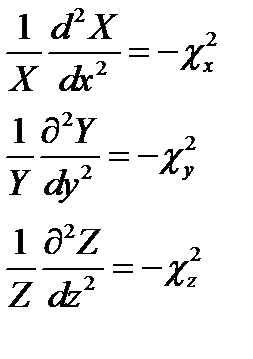 , причём
, причём 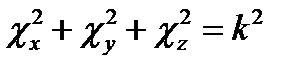 (17.5)
(17.5)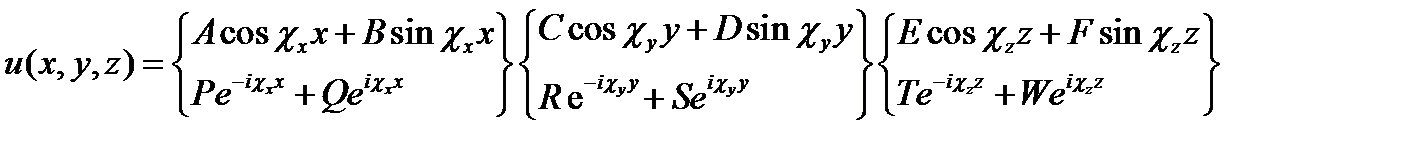 (17.6)
(17.6)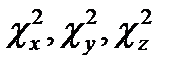 , подчинённых равенству в нижней строке.
, подчинённых равенству в нижней строке.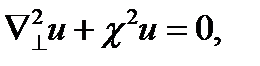 (17.7)
(17.7)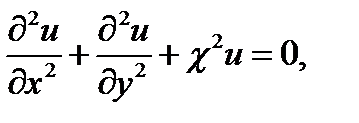 (17.8)
(17.8)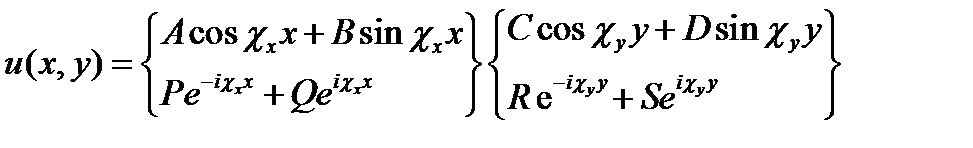 (17.9)
(17.9)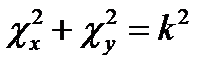
 (17.10)
(17.10)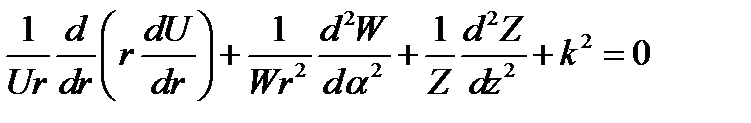 (17.12)
(17.12)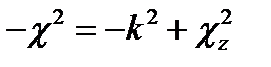 . Поэтому имеем следующие уравнения:
. Поэтому имеем следующие уравнения: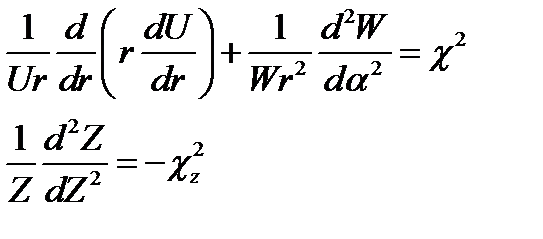
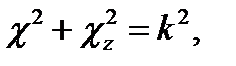 (17.13)
(17.13)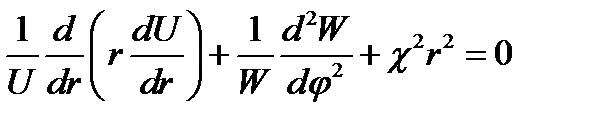 .
.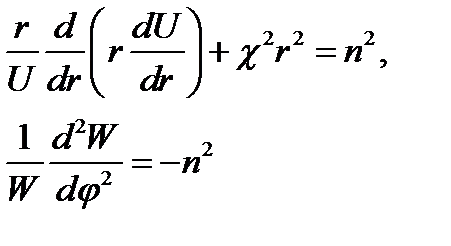 (17.14)
(17.14)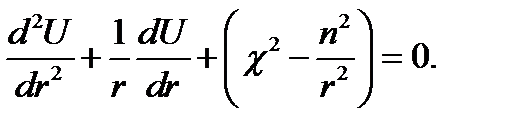 (17.15)
(17.15)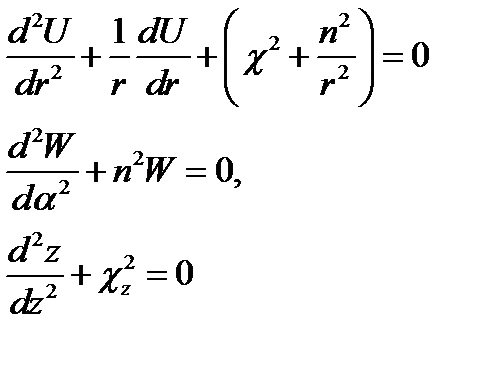
 (17.16)
(17.16)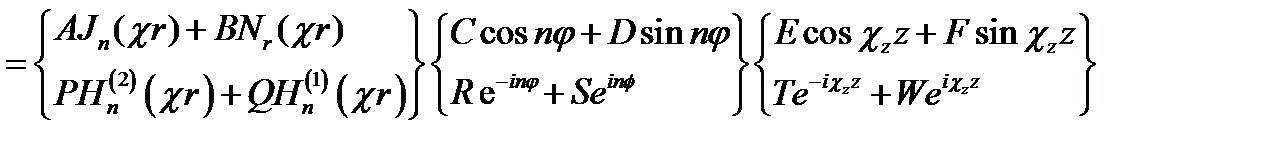 17.17
17.17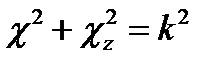
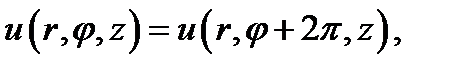 , (17.18)
, (17.18)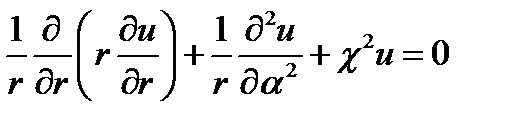 . (17.19)
. (17.19)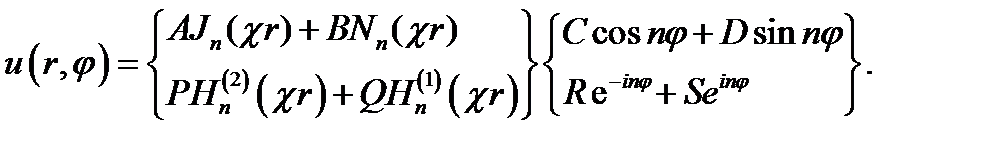 (17.20)
(17.20)


