10.1. Предварительные сведения.Уже отмечалось (см. п.7), что решения уравнения Лапласа
 (10.1)
(10.1)
образуют класс функций, называемых гармоническими. Важное значение имеют граничные задачи для уравнения Лапласа, когда требуется найти решение 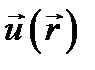 уравнения. (10.1) в области V при некоторых сведениях о его поведении на границе S.
уравнения. (10.1) в области V при некоторых сведениях о его поведении на границе S.
Задача называется внутренней, если поверхность S выделяет из пространства ограниченный объём V;при этом поверхность может быть простой или составной, т. е. состоять из нескольких изолированных частей (S = S1 + S2 + S3).
Если же объем V остаётся неограниченным, то задача называется внешней; в этом случае можно сказать, что полная граница области V состоит из поверхности S (возможно, составной) и отнесённой в бесконечность поверхности S'. Ниже мы рассмотрим граничные задачи для уравнения Лапласа двух наиболее распространённых типов: задачу Дирихле и задачу Неймана.
Предварительно выведём вспомогательные соотношения, которые будут использоваться при исследовании гармонических функций. Полагая в первой формуле Грина (5.13)  , где
, где  какая-либо гармоническая функция, имеем:
какая-либо гармоническая функция, имеем:
 (10.2)
(10.2)
Далее, взяв в (5.13)  , получим
, получим
 (10.3)
(10.3)
10.2. Задача Дирихле. Граничная задача этого типа формулируется следующим образом:
 в V, (10.4)
в V, (10.4)
 на S,
на S,
т. е. требуется найти решение уравнения Лапласа в области V при условии, что на границе S оно равно заданной функции f(r).
Рассмотрим сначала, частный случай внутренней задачи Дирихле, когда  , т. е. граничное условие имеет вид:
, т. е. граничное условие имеет вид:
 на S. (10.5)
на S. (10.5)
Легко убедиться, что единственное решение этой задачи тождественно равно нулю. Действительно, принимая во внимание (10.5), из (10.2) находим:
 , (10.6)
, (10.6)
откуда

 const.
const.
Но так как  на S, то const = 0, и
на S, то const = 0, и
 (10.7)
(10.7)
Для внешней задачи Дирихле с граничным условием (10.5) рассуждения повторяются, но надо учесть ещё, что полная граница объема V есть теперь S + S′ а потому равенство (10.6), влекущее окончательный вывод (10.7), будет следовать из (10.2) только при дополнительном условии:
 (10.8)
(10.8)
Это условие выполняется для регулярных в бесконечности (см. п. 9.3) решений. В самом деле, взяв в качестве S′ сферическую поверхность радиуса r и полагая  , а следовательно;
, а следовательно;  находим, что интеграл есть величина порядка
находим, что интеграл есть величина порядка  , в бесконечности исчезающая.
, в бесконечности исчезающая.
На основании полученных результатов немедленно устанавливается, что решение общей задачи Дирихле (10.4) единственно; при этом подразумевается регулярность решения в бесконечности, когда задача является внешней. Ведь если имеются два различных решения 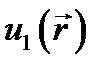 и
и  , то их разность
, то их разность
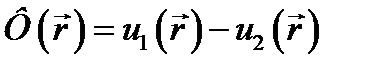
- это решение задачи Дирихле с граничным условием (10.5), а потому в соответствии с (10.7) Ф  = 0, т. е.
= 0, т. е.
 (10.9)
(10.9)
Двух различных решений, таким образом, быть не может.
10.3. Задача Неймана. Согласно формулировке задачи Неймана,
 в V, (10.10)
в V, (10.10)
 на S,
на S,
и требуется найти решение уравнения Лапласа в области V при условии, что на границе S его нормальная производная равна заданной функции f  . Как и задача Дирихле, задача Неймана может быть внутренней и внешней.
. Как и задача Дирихле, задача Неймана может быть внутренней и внешней.
Для внутренней задачи Неймана из (10.3) следует, что
 (10.11)
(10.11)
т. е. функция  в (10.10) не может задаваться произвольно, а должна удовлетворять записанному требованию (10.11).
в (10.10) не может задаваться произвольно, а должна удовлетворять записанному требованию (10.11).
В случае же внешней задачи, поскольку полная граница объема V есть S+S' ,(10.3) принимает вид:
 (10.12)
(10.12)
Требование (10.11) при этом уже не налагается: первый интеграл в (10.12) нулю не равен. Действительно, хотя по-прежнему мы рассматриваем только регулярные в бесконечности решения, второй интеграл в (10.12) не должен обязательно исчезать при отнесении S ' в бесконечность (здесь в отличие от (10.8) интегрируемая функция есть лишь 0(1/r2)).
Переходя к частному случаю, возьмём в (10.10)  , т. е. используем граничное условие
, т. е. используем граничное условие
 на S. (10.13)
на S. (10.13)
Для внутренней задачи в силу (10.13) мы получим из (10.2) равенство (10.6), откуда  и, следовательно,
и, следовательно,
 const, (внутренняя задача), (10.14)
const, (внутренняя задача), (10.14)
т. е. решение внутренней задачи Неймана при данном граничном условии есть константа. Этот вывод распространяется и на регулярные в бесконечности решения внешней задачи, так как интеграл (10.8) при отнесении границы S ' в бесконечность исчезает, как это было в аналогичной задаче Дирихле. Но из всех  const регулярно в бесконечности только
const регулярно в бесконечности только  0. Таким образом, внешняя задача Неймана при граничном условии (10.13) имеет решение
0. Таким образом, внешняя задача Неймана при граничном условии (10.13) имеет решение
 , (внешняя задача). (10.14а)
, (внешняя задача). (10.14а)
Рассматривая затем общую задачу Неймана (10.10), предположим, что она имеет два различных решения  и
и 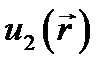 .Их разность есть решение задачи Неймана при условии (10.13). Поэтому согласно (10.14)
.Их разность есть решение задачи Неймана при условии (10.13). Поэтому согласно (10.14)
 = const (внутренняя задача), (10.15)
= const (внутренняя задача), (10.15)
т. е, решения могут различаться на постоянную, и
 (внешняя задача), (10.15а)
(внешняя задача), (10.15а)
ввиду (10.14а); в этом случае решение единственно.
Метод разделения переменных
11.1. Сущность метода. Разделение переменных в цилиндрических координатах. При решении граничных задач для различных уравнений с частными производными широко используется так называемый метод разделения переменных, позволяющий свести исходную задачу вообще к трем (а в двумерном случае к двум) задачам для обыкновенных дифференциальных уравнений. Этот метод применим при пользовании декартовой, цилиндрической, сферической и несколькими другими системами координат, когда граничная поверхность задачи может рассматриваться как координатная (или иногда совокупность координатных поверхностей). Позднее мы будем применять метод разделения переменных к различным задачам электродинамики, а в данной главе он используется при решении граничных задач для уравнения Лапласа.
Поясним сущность метода разделения переменных на следующем примере. Пусть требуется найти решение граничной задачи для уравнения Лапласа (задачи Дирихле или Неймана, внутренней или внешней) для цилиндрической области при условии, что решение не зависит от продольной координаты z, т. е. неизменно вдоль оси цилиндра. Ввиду этого задача является двумерной: решение ищется как функция координат в плоскости поперечного сечении цилиндра. Согласно (6.17) уравнение Лапласа принимает вид:
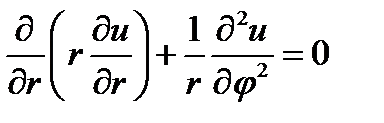 (11.1)
(11.1)
Предположим, что искомое решение 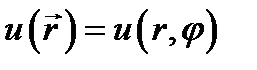 представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной:
представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной:
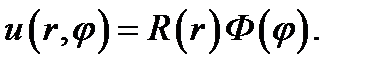 (11.2)
(11.2)
Мы увидим в дальнейшем, что это предположение оправдывается. Подстановка выражения (11.2) в уравнение Лапласа (11.1) с последующим умножением обоих слагаемых на r/RФ дает:
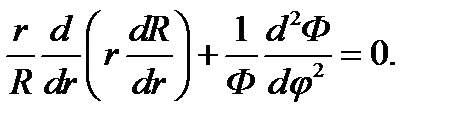 (11.3)
(11.3)
Таким образом, путём довольно простых операций удалось представить левую часть уравнения в виде суммы функций независимых аргументов: первое слагаемое в (11.3) зависит только от r, а второе - от φ. Простые рассуждения показывают, что эти слагаемые - константы. Действительно, фиксируя некоторое значение r и делая тем самым заведомо постоянным первое слагаемое, будем менять в возможных пределах φ, на что мы имеем право в силу независимости обоих слагаемых. Второе слагаемое, как видно из (11.3), остается при этом постоянным и равным первому с обратным знаком. Точно так же можно зафиксировать φ и убедиться, что первое слагаемое постоянно при изменении r. Постоянная величина, которой равно первое слагаемое, пока неизвестна; обозначим ее п2 и назовем постоянной разделения. Приравнивая слагаемые (11.3) постоянным п2 и - п2 соответственно, получаем после очевидных преобразований следующие два обыкновенных дифференциальных уравнения:
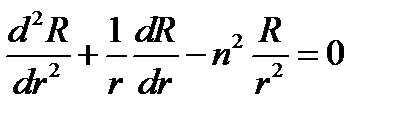 (11.4)
(11.4)
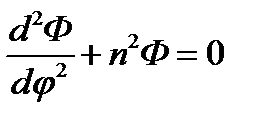
Это и есть результат «разделения переменных».
Теперь ясно, что решение уравнения Лапласа (11.1) в форме (11.2) существует, поскольку R и Ф есть решения обыкновенных дифференциальных уравнений (11.4). Найдём решения этих уравнений.
Начнем с более простого уравнения, стоящего во второй строке (11.4) и уже встречавшегося в п.7. Используя первую форму записи (7.8), выразим его общее решение в виде:
Ф = A cos nφ + В sin nφ, (11.5)
где А и В - произвольные постоянные. Поскольку функция Ф должна иметь период 2π, т. е.
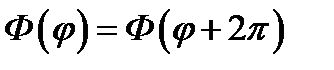 (11.6)
(11.6)
(возвращение в прежнюю точку после обхода), то
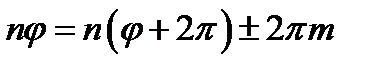 ,
,
где т - целое число или нуль. Отсюда следует, что
n=0, ± 1, ± 2,..., (11.7)
т. е. дробные значения п исключены. Ввиду неопределенности А и В,в (11.7) достаточно оставить положительные числа и нуль. В частности, при п = 0 из (11.5) находим, что Ф = А = const. Заметим, что при п = 0 уравнение во второй строчке (11.4) имеет и более общее непериодическое решение
W = Aφ + B,
которое ввиду (11.6) не является решением нашей задачи.
Уравнение в первой строчке (11.4) имеет общее решение
U = 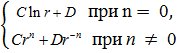 (11.8)
(11.8)
где С и D - произвольные постоянные.
Итак, решение уравнения Лапласа (11.1) представлено в виде произведения функций (11.2), определяемых формулами (11.5) и (11.8).
Значения произвольных констант, входящих в полученные решения, определяются, естественно, конкретными граничными условиями задачи.



 (10.1)
(10.1)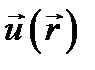 уравнения. (10.1) в области V при некоторых сведениях о его поведении на границе S.
уравнения. (10.1) в области V при некоторых сведениях о его поведении на границе S. , где
, где  какая-либо гармоническая функция, имеем:
какая-либо гармоническая функция, имеем: (10.2)
(10.2) , получим
, получим (10.3)
(10.3) на S,
на S, , т. е. граничное условие имеет вид:
, т. е. граничное условие имеет вид: на S. (10.5)
на S. (10.5) , (10.6)
, (10.6)
 const.
const. на S, то const = 0, и
на S, то const = 0, и (10.7)
(10.7) (10.8)
(10.8) , а следовательно;
, а следовательно;  находим, что интеграл есть величина порядка
находим, что интеграл есть величина порядка  , в бесконечности исчезающая.
, в бесконечности исчезающая.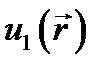 и
и  , то их разность
, то их разность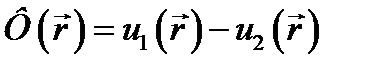
 = 0, т. е.
= 0, т. е. (10.9)
(10.9) в V, (10.10)
в V, (10.10) на S,
на S, . Как и задача Дирихле, задача Неймана может быть внутренней и внешней.
. Как и задача Дирихле, задача Неймана может быть внутренней и внешней. (10.11)
(10.11) в (10.10) не может задаваться произвольно, а должна удовлетворять записанному требованию (10.11).
в (10.10) не может задаваться произвольно, а должна удовлетворять записанному требованию (10.11). (10.12)
(10.12) , т. е. используем граничное условие
, т. е. используем граничное условие на S. (10.13)
на S. (10.13) и, следовательно,
и, следовательно, const, (внутренняя задача), (10.14)
const, (внутренняя задача), (10.14) const регулярно в бесконечности только
const регулярно в бесконечности только  0. Таким образом, внешняя задача Неймана при граничном условии (10.13) имеет решение
0. Таким образом, внешняя задача Неймана при граничном условии (10.13) имеет решение , (внешняя задача). (10.14а)
, (внешняя задача). (10.14а) и
и 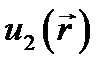 .Их разность есть решение задачи Неймана при условии (10.13). Поэтому согласно (10.14)
.Их разность есть решение задачи Неймана при условии (10.13). Поэтому согласно (10.14) = const (внутренняя задача), (10.15)
= const (внутренняя задача), (10.15) (внешняя задача), (10.15а)
(внешняя задача), (10.15а)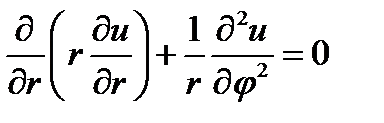 (11.1)
(11.1)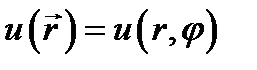 представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной:
представляет собой произведение двух функций, одна из которых есть функция радиальной координаты, а другая - азимутальной: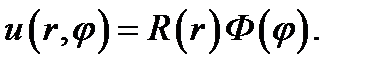 (11.2)
(11.2)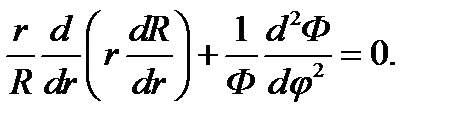 (11.3)
(11.3)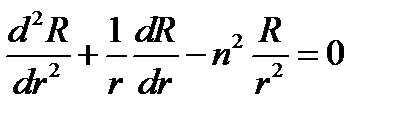 (11.4)
(11.4)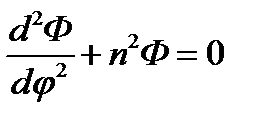
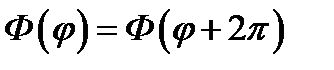 (11.6)
(11.6)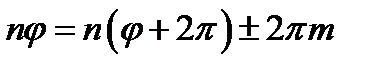 ,
,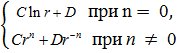 (11.8)
(11.8)


