 3.1. Силовые линии и поток вектора.
3.1. Силовые линии и поток вектора. Желая исследовать какое-либо векторное поле, мы можем выделить определенный объем
V и сосредоточить внимание на картине силовых линий в этом объеме. На рис. 3.1 изображено несколько характерных типов расположения силовых линий, которые, возможно, при этом встретятся (пунктиром изображена граница
S области
V). Как видно, в одном из случаев внутри объема находится «источник» силовых линий (рис. 3.1а) либо «cток» (рис. 3.16), т. е. линии выходят из
V или, соответственно, входят в
V через границу
S. Но силовые линии могут также пронизывать
V насквозь, не начинаясь и не кончаясь в этой области (рис. 3.1е). Наконец, замкнутые силовые линии могут совершенно не пересекать границу
S (рис. 3.1г). Вообще, когда задана векторная функция и изучается соответствующее векторное поле, закономерен вопрос, является ли некоторая точка
Р источником (стоком) или не является. На такой вопрос,как будет видно, легко ответить аналитически, не прибегая к помощи графики.
Начнем с понятия потока вектора. Потоком вектора F через границу (поверхность) S называется интеграл
 , (3.1)
, (3.1)
где векторный дифференциал поверхности  понимается как произведение обычного дифференциала ds на единичный вектор нормали
понимается как произведение обычного дифференциала ds на единичный вектор нормали  к поверхности, т.е.
к поверхности, т.е.  ; положительной считают внешнюю нормаль (что для замкнутой поверхности определяется однозначно). Процесс получения подынтегрального выражения при вычислении потока вектора поясняет рис. 3.2. Подынтегральное выражение, будучи скалярным произведением двух векторов, положительно, когда угол между ними острый, и отрицательно при тупом угле.
; положительной считают внешнюю нормаль (что для замкнутой поверхности определяется однозначно). Процесс получения подынтегрального выражения при вычислении потока вектора поясняет рис. 3.2. Подынтегральное выражение, будучи скалярным произведением двух векторов, положительно, когда угол между ними острый, и отрицательно при тупом угле.
Рис 3 2
Поэтому поток вектора обязательно положителен, если все силовые линии выходят через рассматриваемую поверхность наружу (образуя острый угол с её внешней нормалью), как, например, на рис. 3.1а, и отрицателен, когда они входят внутрь (рис. 3.16). В случае замкнутой поверхности S обычно пишут:
 (3.1а)
(3.1а)
Покажем, что поток вектора 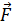 через поверхность S можно измерять, числом пересекающих её силовых линий при условии, что их густота характеризует интенсивность поля. Рассмотрим сначала векторный элемент поверхности
через поверхность S можно измерять, числом пересекающих её силовых линий при условии, что их густота характеризует интенсивность поля. Рассмотрим сначала векторный элемент поверхности  (элемент площади Δ s на рис. 3.2 заштрихован). Элементарный поток ΔФ, проходящий через Δs, равен
(элемент площади Δ s на рис. 3.2 заштрихован). Элементарный поток ΔФ, проходящий через Δs, равен
 , (3.2)
, (3.2)
где  - проекция векторного элемента
- проекция векторного элемента  на направление вектора
на направление вектора  Как видно из рис. 3.2,
Как видно из рис. 3.2,  представляет собой площадку, через которую под прямым углом проходят все силовые линии вектора
представляет собой площадку, через которую под прямым углом проходят все силовые линии вектора 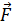 , пересекающие элемент Δ s; число их обозначим Δ N. Густота силовых линий характеризуется отношением Δ N/
, пересекающие элемент Δ s; число их обозначим Δ N. Густота силовых линий характеризуется отношением Δ N/  , а по условию последнее должно быть пропорционально абсолютному значению F вектора
, а по условию последнее должно быть пропорционально абсолютному значению F вектора 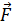 , т. е.
, т. е.
 , (3.3)
, (3.3)
(k - коэффициент пропорциональности). Таким образом, согласно (3.2) и (3.3)
 , (3.4)
, (3.4)
т. е. элементарный поток 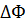 измеряется числом силовых линий, проходящих через соответствующий элемент поверхности. Складывая потоки элементарных площадок, на которые разбита поверхность S, находим:
измеряется числом силовых линий, проходящих через соответствующий элемент поверхности. Складывая потоки элементарных площадок, на которые разбита поверхность S, находим:
 . (3.5)
. (3.5)
Следовательно, полный поток Ф вектора 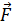 через поверхность S измеряется числом N силовых линий, её пересекающих, что и требовалось показать. При этом число выходящих силовых линий считается положительным, а число входящих - отрицательным. Наконец, необходимо ещё одно замечание. Соотношение (3.5) мы будем рассматривать как точное, хотя практически точность выражения потока числом силовых линий зависит от степени грубости построенной картины. В сущности, формула (3.5) может рассматриваться как точная, если число силовых линий, отнесенных к единице площади, условно считается непрерывной функцией, приращения заменяются дифференциалами, а суммирование потока по элементам - интегрированием.
через поверхность S измеряется числом N силовых линий, её пересекающих, что и требовалось показать. При этом число выходящих силовых линий считается положительным, а число входящих - отрицательным. Наконец, необходимо ещё одно замечание. Соотношение (3.5) мы будем рассматривать как точное, хотя практически точность выражения потока числом силовых линий зависит от степени грубости построенной картины. В сущности, формула (3.5) может рассматриваться как точная, если число силовых линий, отнесенных к единице площади, условно считается непрерывной функцией, приращения заменяются дифференциалами, а суммирование потока по элементам - интегрированием.
3.2. Дивергенция. По определению, дивергенция вектора 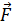 , обозначаемая символом div
, обозначаемая символом div 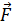 , выражается следующим предельным соотношением:
, выражается следующим предельным соотношением:
 (3.6)
(3.6)
где под S понимается замкнутая поверхность, ограничивающая Δ V.
Для иллюстрации введенного понятия обратимся к рис. 3.3.
Положим, что поток вектора 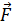 через S для рассматриваемого случая равен Ф, Ф > 0. Одновременно он измеряется числом выходящих через S силовых линий. Поэтому, если предельный переход в (3.6) производить, стягивая S вокруг точки Р (рис. 3.3а), из которой силовые линии выходят, то как бы ни уменьшался объем, поток через его границу останется равным Ф. В пределе при Δ V → 0 получим
через S для рассматриваемого случая равен Ф, Ф > 0. Одновременно он измеряется числом выходящих через S силовых линий. Поэтому, если предельный переход в (3.6) производить, стягивая S вокруг точки Р (рис. 3.3а), из которой силовые линии выходят, то как бы ни уменьшался объем, поток через его границу останется равным Ф. В пределе при Δ V → 0 получим
 в точке Р.
в точке Р.
Если же, стягивая S, мы обойдем точку Р (рис. 3.36), то, начиная с этого момента, число силовых линий, входящих в ΔV, окажется равным числу линий выходящих. Следовательно, понимая предельный переход в (3.6) как стягивание S к любой из точек, не совпадающих с Р, будем иметь:
 вне точки Р.
вне точки Р.

Рис. 3.3
Очевидно, если бы вместо поля с точечным источником мы рассмотрели поле с подобным же стоком (см. рис. 3.1 б), то расхождение везде было бы равно нулю, кроме одной точки, в которой оно имело бы отрицательное значение. В полях же без источников и стоков (рис. 3.1, в, г), расхождение  равно нулю во всех точках. Поля с нулевым расхождением называются соленоидальными; их силовые линии нигде не начинаются и не кончаются: они или замкнуты, или уходят в бесконечность (они могут также оканчиваться на границе области, в которой задано векторное поле).
равно нулю во всех точках. Поля с нулевым расхождением называются соленоидальными; их силовые линии нигде не начинаются и не кончаются: они или замкнуты, или уходят в бесконечность (они могут также оканчиваться на границе области, в которой задано векторное поле).
Из определения оператора дивергенции следует его физический смысл: это растекание физической величины, её расхождение.
3.3. Дивергенция в декартовых координатах.От общего определения дивергенции (3.6) можно перейти к её дифференциальному выражению в декартовой системе координат. Для нахождения  в некоторой точке М (х, у, z)проведём через неё координатные линии и построим, как это показано на рис. 3.5, элементарный параллелепипед. Теперь надо вычислить поток вектора
в некоторой точке М (х, у, z)проведём через неё координатные линии и построим, как это показано на рис. 3.5, элементарный параллелепипед. Теперь надо вычислить поток вектора 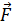 через поверхность этого параллелепипеда. Очевидно, полный поток Ф можно разбить на три части (Ф = Ф1 + Ф2 + Ф3), каждая из которых соответствует двум противоположным граням. Так, Ф 1- это поток через грань 1 и противоположную ей грань 1 ' (невидимую на рис.). Чем меньше грань, тем с большим основанием при вычислении потока можно заменять интеграл (3.1) приближенным выражением
через поверхность этого параллелепипеда. Очевидно, полный поток Ф можно разбить на три части (Ф = Ф1 + Ф2 + Ф3), каждая из которых соответствует двум противоположным граням. Так, Ф 1- это поток через грань 1 и противоположную ей грань 1 ' (невидимую на рис.). Чем меньше грань, тем с большим основанием при вычислении потока можно заменять интеграл (3.1) приближенным выражением

 Рис. 3.5
Рис. 3.5
(Δ S -площадь грани, 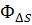 - поток через неё). Поступая так, учтём, что на гранях 1 и 1 ' -единичный вектор внешней нормали равен
- поток через неё). Поступая так, учтём, что на гранях 1 и 1 ' -единичный вектор внешней нормали равен  соответственно, а Δ S = Δ y Δz. Таким образом,
соответственно, а Δ S = Δ y Δz. Таким образом,
 .
.
Заменив 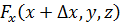 через
через

найдем:
 ,
,
и точно также:

Согласно (3.6) в точке М (х, у, z)

(в пределе приближённые выражения становятся точными), т. е.
 (3.7)
(3.7)
 3.4. Теорема Остроградского-Гаусса.
3.4. Теорема Остроградского-Гаусса. В заключение получим важное соотношение, которое составляет содержание теоремы Остроградского-Гаусса. Рассматривая объем
V с граничной поверхностью S (рис. 3.6), разобьём его на элементы ΔV
i. Каждый из этих элементарных объёмов может быть настолько мал, что ошибка определения дивергенции вектора
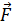
внутри ΔV
i по приближенной формуле

( есть
есть 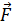 в ΔV i) вместо (3.6) будет меньше некоторой наперёд заданной величины. Поэтому справедливо:
в ΔV i) вместо (3.6) будет меньше некоторой наперёд заданной величины. Поэтому справедливо:

где ε -как угодно малая положительная величина, соответственно которой выбран размер ΔV i.
Полагая, что неравенство (с данным ε) выполнено дли каждого элемента, произведём суммирование по i, которое даст:

Дело в том, что поверхностные интегралы по всем внутренним границам, разделяющим смежные элементы ΔV i, взаимно уничтожаются: на каждой общей границе (см. рис. 3.6) нормали для двух соседних элементов противоположны. Поэтому остаются лишь поверхностные интегралы по тем частям поверхностей элементов, которые составляют внешнюю границу S.
Переходя в пределе при N →∞ (бесконечное «измельчение» элементов ΔV i) от суммы к интегралу и учитывая произвольную малость ε, получаем соотношение:
 (3.8)
(3.8)
Это и есть формулировка теоремы Остроградского-Гаусса, согласно которой объёмный интеграл от дивергенции вектора равен потоку этого вектора через замкнутую граничную поверхность.
Ротор. Теорема Стокса
4.1. Ротор. В 1.2 было показано, что для полей потенциальных циркуляция при однозначности потенциала равна нулю (п. 4). Однако в общем случае циркуляция вектора 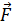 по некоторому контуру L не должна обязательно быть равной нулю. Подобно потоку вектора, циркуляция также может быть использована для локальной характеристики поля. При этом возникает понятие ротора вектора
по некоторому контуру L не должна обязательно быть равной нулю. Подобно потоку вектора, циркуляция также может быть использована для локальной характеристики поля. При этом возникает понятие ротора вектора 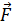 , обозначаемого символом rot
, обозначаемого символом rot 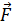 . По определению, rot
. По определению, rot 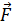 есть вектор, проекция которого на произвольное направление
есть вектор, проекция которого на произвольное направление 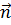 выражается следующим образом:
выражается следующим образом:
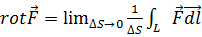 (4.1)
(4.1)
где Δ S - площадка, выбранная так, что 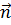 есть нормаль к ней, a L - контур этой площадки, направление обхода которого при интегрировании составляет с нормалью правовинтовую систему (если смотреть вдоль нормали, то обход производится по часовой стрелке).
есть нормаль к ней, a L - контур этой площадки, направление обхода которого при интегрировании составляет с нормалью правовинтовую систему (если смотреть вдоль нормали, то обход производится по часовой стрелке).
4.2. Ротор в декартовых координатах. Как и дивергенцию, ротор вектора нетрудно представить в виде дифференциального выражения в декартовой системе координат. Обратимся к рис. 4.1, на котором через произвольную точку М (х, у, z)проведены три координатные линии и построены элементарные площадки, лежащие в координатных плоскостях. Желая сначала найти проекцию вектора 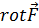 на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)
на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)
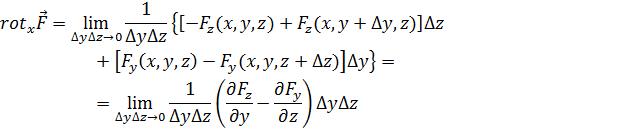
Таким образом,
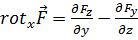 (4.2a)
(4.2a)
Совершенно аналогично получаем:
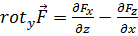 , (4.2б)
, (4.2б)
и
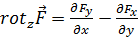 . (4.2в)
. (4.2в)
Эти три равенства удобно объединяются в форме определителя:
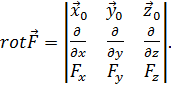 (4.3)
(4.3)
Нетрудно показать, что потенциальные поля являются обязательно «безвихревыми», т. е. для всякого вектора 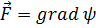 будет
будет 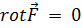 . Чтобы проверить тождество
. Чтобы проверить тождество
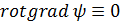 , (4.4)
, (4.4)
достаточно рассмотреть какую-либо одну его проекцию. Так, составляя по формулам (4.2 а)и (2.4 а)проекцию этого вектора на ось х, имеем:
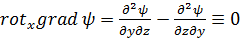 .
.
Другой важный факт заключается в том, что дивергенция вихревого поля тождественно равна нулю, т. е. такое векторное поле соленоидально (3.2):
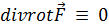 . (4.5)
. (4.5)
Действительно,
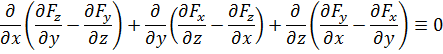
Из определения ротора, его можно трактовать в физическом смысле как вихрь.
4.3. Теорема Стокса. Перейдем, наконец, к теореме Стокса, содержание которой выражается равенством:
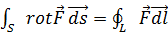 , (4.6)
, (4.6)
где S - некоторая поверхность, a L - её контур, направление обхода которого при интегрировании согласовано с направлением положительной нормали к S, как и ранее. Согласно теореме Стокса, поток ротора некоторого вектора F через поверхность S равен циркуляции самого вектора по соответствующему контуру L.
Чтобы убедиться в справедливости теоремы Стокса, разобьем произвольную поверхность S на достаточно малые элементарные площадки Δ si (рис. 4.3) и для определения ротора 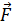 внутри Δs i воспользуемся приближённым соотношением
внутри Δs i воспользуемся приближённым соотношением
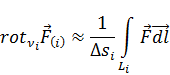
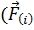 есть
есть 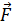 внутри Δ si) вместо (4.1). Поскольку точность этого равенства может быть как угодно велика (достаточно лишь взять соответственно малые размеры элемента Δ si), то
внутри Δ si) вместо (4.1). Поскольку точность этого равенства может быть как угодно велика (достаточно лишь взять соответственно малые размеры элемента Δ si), то
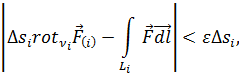
где ε – наперёд заданная сколь угодно малая положительная величина.
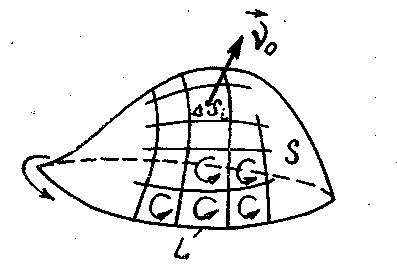
Рис. 4.3
Выбрав все элементы достаточно малыми, произведём суммирование по i и получим:
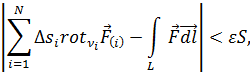
где фигурирует циркуляция 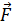 по граничному контуру L всей поверхности S, поскольку при суммировании части циркуляции по общим границам смежных элементов
по граничному контуру L всей поверхности S, поскольку при суммировании части циркуляции по общим границам смежных элементов 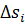 взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.
взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.
Неограниченно измельчая все элементы 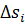 и переходя соответственно этому от суммы к интегралу (N →∞), а также учитывая произвольную малость ε, приходим от предыдущего равенства к формулировке теоремы Стокса (4.6).
и переходя соответственно этому от суммы к интегралу (N →∞), а также учитывая произвольную малость ε, приходим от предыдущего равенства к формулировке теоремы Стокса (4.6).




 , (3.1)
, (3.1) понимается как произведение обычного дифференциала ds на единичный вектор нормали
понимается как произведение обычного дифференциала ds на единичный вектор нормали  к поверхности, т.е.
к поверхности, т.е.  ; положительной считают внешнюю нормаль (что для замкнутой поверхности определяется однозначно). Процесс получения подынтегрального выражения при вычислении потока вектора поясняет рис. 3.2. Подынтегральное выражение, будучи скалярным произведением двух векторов, положительно, когда угол между ними острый, и отрицательно при тупом угле.
; положительной считают внешнюю нормаль (что для замкнутой поверхности определяется однозначно). Процесс получения подынтегрального выражения при вычислении потока вектора поясняет рис. 3.2. Подынтегральное выражение, будучи скалярным произведением двух векторов, положительно, когда угол между ними острый, и отрицательно при тупом угле. (3.1а)
(3.1а)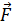 через поверхность S можно измерять, числом пересекающих её силовых линий при условии, что их густота характеризует интенсивность поля. Рассмотрим сначала векторный элемент поверхности
через поверхность S можно измерять, числом пересекающих её силовых линий при условии, что их густота характеризует интенсивность поля. Рассмотрим сначала векторный элемент поверхности  (элемент площади Δ s на рис. 3.2 заштрихован). Элементарный поток ΔФ, проходящий через Δs, равен
(элемент площади Δ s на рис. 3.2 заштрихован). Элементарный поток ΔФ, проходящий через Δs, равен , (3.2)
, (3.2) - проекция векторного элемента
- проекция векторного элемента  на направление вектора
на направление вектора  Как видно из рис. 3.2,
Как видно из рис. 3.2,  представляет собой площадку, через которую под прямым углом проходят все силовые линии вектора
представляет собой площадку, через которую под прямым углом проходят все силовые линии вектора  , а по условию последнее должно быть пропорционально абсолютному значению F вектора
, а по условию последнее должно быть пропорционально абсолютному значению F вектора  , (3.3)
, (3.3) , (3.4)
, (3.4)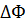 измеряется числом силовых линий, проходящих через соответствующий элемент поверхности. Складывая потоки элементарных площадок, на которые разбита поверхность S, находим:
измеряется числом силовых линий, проходящих через соответствующий элемент поверхности. Складывая потоки элементарных площадок, на которые разбита поверхность S, находим: . (3.5)
. (3.5) (3.6)
(3.6) в точке Р.
в точке Р. вне точки Р.
вне точки Р.
 равно нулю во всех точках. Поля с нулевым расхождением называются соленоидальными; их силовые линии нигде не начинаются и не кончаются: они или замкнуты, или уходят в бесконечность (они могут также оканчиваться на границе области, в которой задано векторное поле).
равно нулю во всех точках. Поля с нулевым расхождением называются соленоидальными; их силовые линии нигде не начинаются и не кончаются: они или замкнуты, или уходят в бесконечность (они могут также оканчиваться на границе области, в которой задано векторное поле). в некоторой точке М (х, у, z)проведём через неё координатные линии и построим, как это показано на рис. 3.5, элементарный параллелепипед. Теперь надо вычислить поток вектора
в некоторой точке М (х, у, z)проведём через неё координатные линии и построим, как это показано на рис. 3.5, элементарный параллелепипед. Теперь надо вычислить поток вектора 
 Рис. 3.5
Рис. 3.5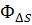 - поток через неё). Поступая так, учтём, что на гранях 1 и 1 ' -единичный вектор внешней нормали равен
- поток через неё). Поступая так, учтём, что на гранях 1 и 1 ' -единичный вектор внешней нормали равен  соответственно, а Δ S = Δ y Δz. Таким образом,
соответственно, а Δ S = Δ y Δz. Таким образом, .
.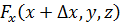 через
через
 ,
,

 (3.7)
(3.7)

 есть
есть 

 (3.8)
(3.8)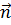 выражается следующим образом:
выражается следующим образом: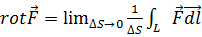 (4.1)
(4.1)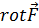 на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)
на ось х, мы должны вычислить циркуляцию вектора F по контуру первой площадки и перейти к пределу согласно (4.1). Действия при этом похожи на производившиеся в преыдущем разделе. Итак, на основании (4.1)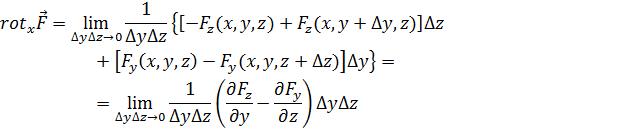
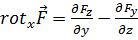 (4.2a)
(4.2a)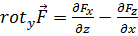 , (4.2б)
, (4.2б)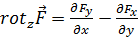 . (4.2в)
. (4.2в)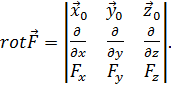 (4.3)
(4.3)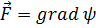 будет
будет 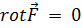 . Чтобы проверить тождество
. Чтобы проверить тождество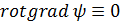 , (4.4)
, (4.4)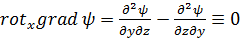 .
.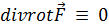 . (4.5)
. (4.5)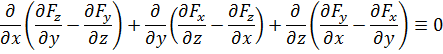
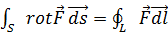 , (4.6)
, (4.6)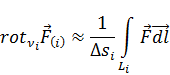
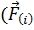 есть
есть 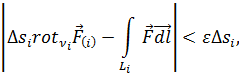

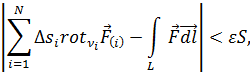
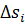 взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.
взаимно уничтожались; действительно, как видно из рис. 4.3, направления обходов общих участков границ смежных элементов противоположны.

