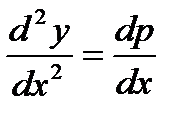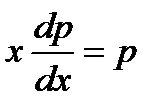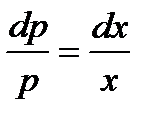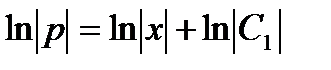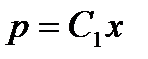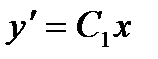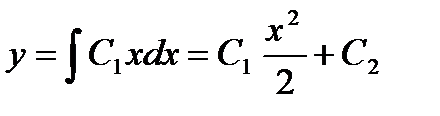Рассмотрим уравнения вида

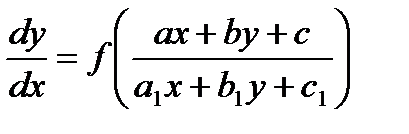
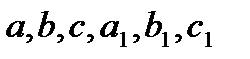 — постоянные
— постоянные
Если 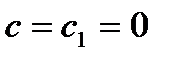 , то уравнение является однородным. Если хотя бы одно из чисел
, то уравнение является однородным. Если хотя бы одно из чисел 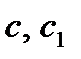 отлично от нуля, то следует различать два случая.
отлично от нуля, то следует различать два случая.
1) 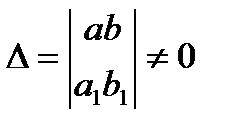
Вводя новые переменные 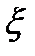 и
и  по формулам
по формулам 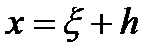 ,
, 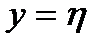 приведем уравнение к виду
приведем уравнение к виду 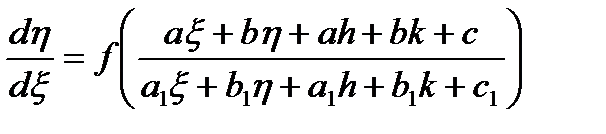
Выбирая h и k как решение системы линейных уравнений
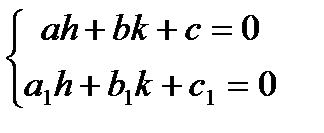
получаем однородное уравнение 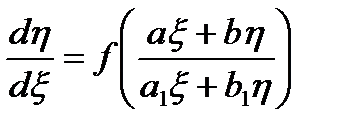 найдя его общий интеграл и заменив
найдя его общий интеграл и заменив 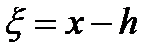 ,
, 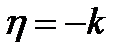 получаем общий интеграл уравнения
получаем общий интеграл уравнения
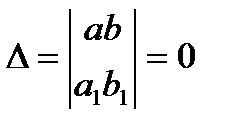 и уравнение имеет вид
и уравнение имеет вид
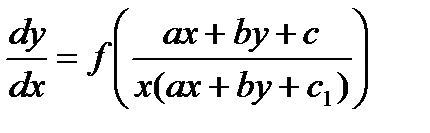
Подстановка 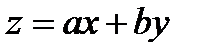 приводит его к уравнению с разделяющими переменными.
приводит его к уравнению с разделяющими переменными.
Пример 4.2. Решить уравнение 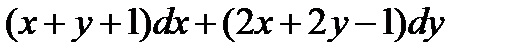
Решение. Система линейных алгебраических уравнений 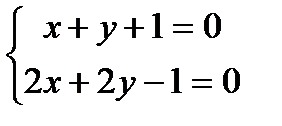 несовместна. В том случае метод, применённый в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку
несовместна. В том случае метод, применённый в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку 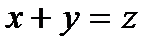 ,
, 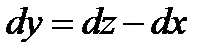 . Уравнение примет вид
. Уравнение примет вид
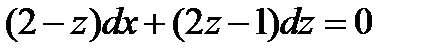
Разделяя, переменные получаем
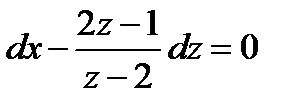 ,
, 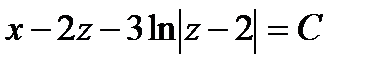
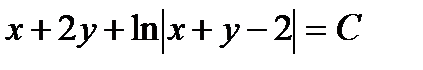
Линейные уравнения первого порядка.
Линейным дифференциальным уравнением 1-ого порядка называется уравнение, линейное относительно неизвестной функции и её производной
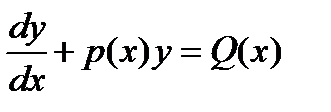 . (1)
. (1)
Решение линейного уравнения ищем в виде 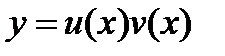
Подставляя в (1), после преобразования получаем 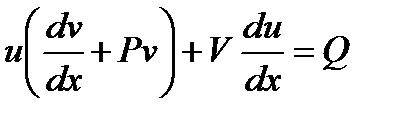
Выберем v такой чтобы 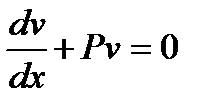 найдём
найдём 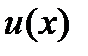 , и следовательно и решение
, и следовательно и решение 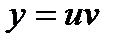
Пример 5.1. Решить задачу Коши
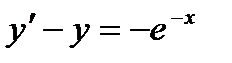 ,
, 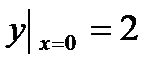
Решение. Это линейное уравнение. Ищем общее решение в виде 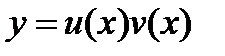 , имеем
, имеем 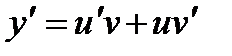 . Подставляя выражения для
. Подставляя выражения для 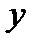 и
и 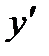 в данное уравнение, будем иметь
в данное уравнение, будем иметь
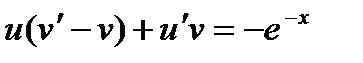
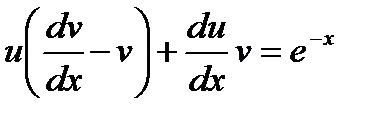
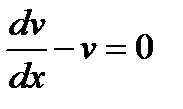 ,
, 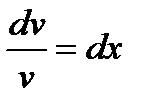 ,
, 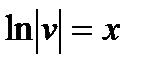 ,
, 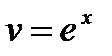
Для определения u имеем уравнение
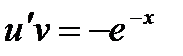 ,
,
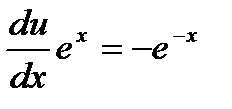 ,
, 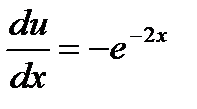 ,
, 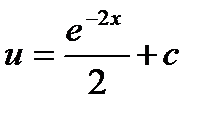
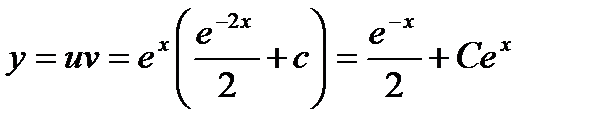
Найдём C: 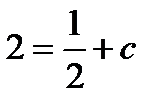 ,
, 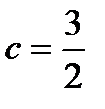 ;
;
Итак, решением поставленной задачи Коши будет
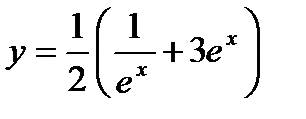 .
.
6. Уравнение Бернулли имеет вид 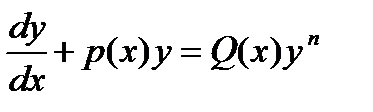 , где
, где 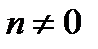
с помощью замены переменной 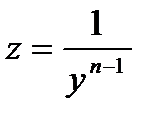 уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.
уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.
Пример 6.1. Решить уравнение 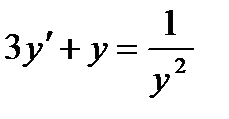
Решение. Умножим обе части уравнения на 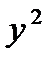
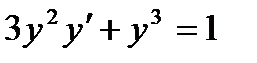
Положим 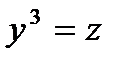 , тогда
, тогда 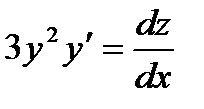 , подставим в уравнение
, подставим в уравнение
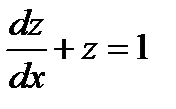
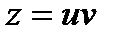 ,
, 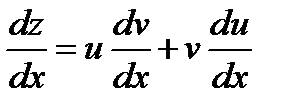
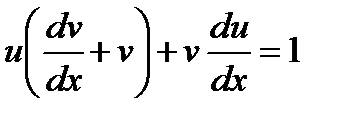 ,
, 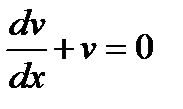 ,
, 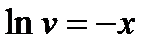 ,
, 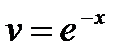
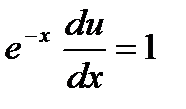 ,
, 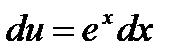 ,
, 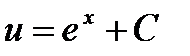
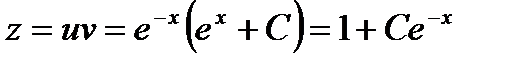
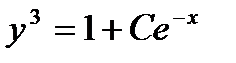
Уравнения в полных дифференциалах.
Дифференциальное уравнение вида 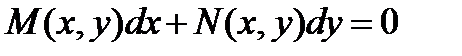 (1) называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции
(1) называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции 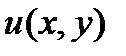 т.е.
т.е.
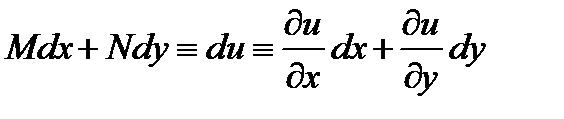
Для того чтобы (1) являлось уравнением в полных дифференциалах необходимо и достаточно, чтобы в некоторой области D изменения переменных x и y выполнялось условие 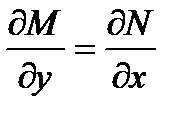
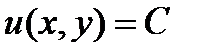
Общий интеграл уравнения (1) имеет вид 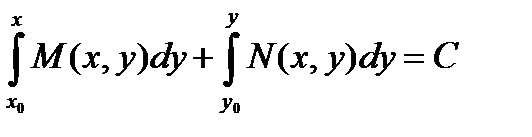
Пример 7.1. Решить уравнение
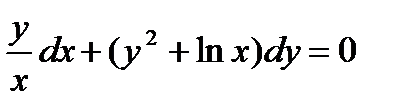
Решение. Проверим, что данное уравнение является уравнением в полных дифференциалах
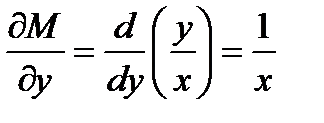 ,
, 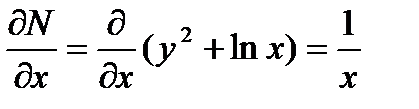 , так что
, так что 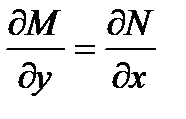
То данное уравнение есть уравнение в полных дифференциалах и 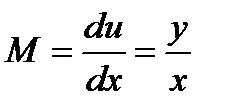 ,
, 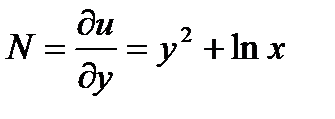 , поэтому
, поэтому 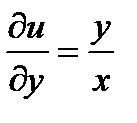 , проинтегрируем
, проинтегрируем 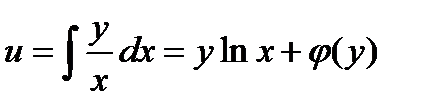
где 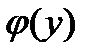 пока неопределённая функция.
пока неопределённая функция.
Частная производная 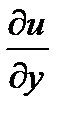 найденной функции
найденной функции 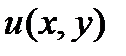 должна равняться
должна равняться
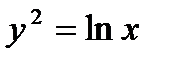 ,
,
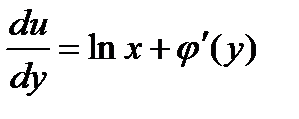 ,
,
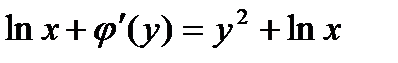
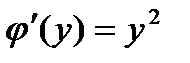
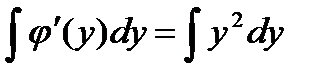
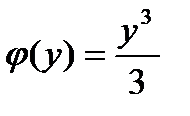
Общий интеграл имеет вид 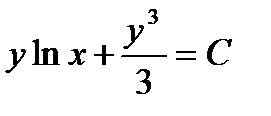
Интегрирующий множитель
В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удаётся подобрать функцию 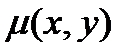 , после умножения на которую, левая часть (1) превращается в полный дифференциал
, после умножения на которую, левая часть (1) превращается в полный дифференциал 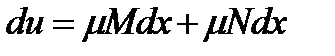 .
.
Такая функция 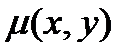 называется интегрирующим множителем из определения интегрирующего множителя
называется интегрирующим множителем из определения интегрирующего множителя 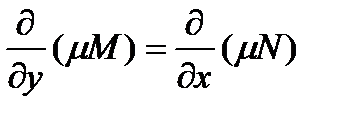 или
или 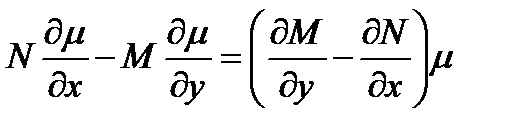
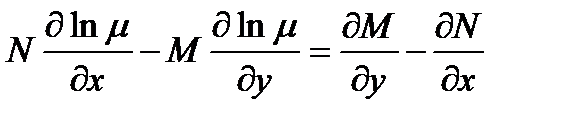 (2)
(2)
Некоторые частные случаи, когда удаётся легко найти интегрирующий множитель.
1. Если 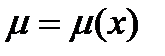 , то
, то 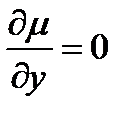 и уравнение (2) примет вид
и уравнение (2) примет вид
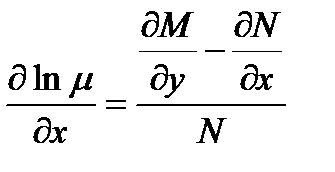 (3)
(3)
Для существования интегрирующего множителя, не зависящего от y, необходимо и достаточно, чтобы правая часть (3) была функцией только от x.
Пример 8.1. Решить уравнения
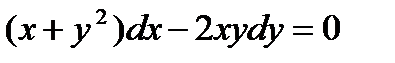
Решение. 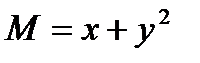 ,
, 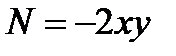 , имеем
, имеем 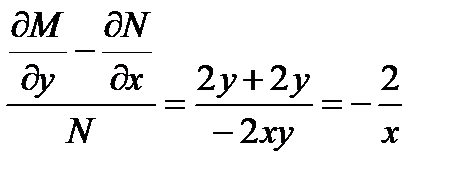 , следовательно
, следовательно 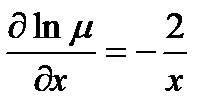 ,
, 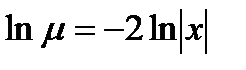 ,
, 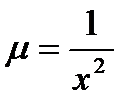
Уравнение 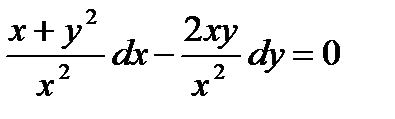 в полных дифференциалах
в полных дифференциалах
Его можно представить в виде 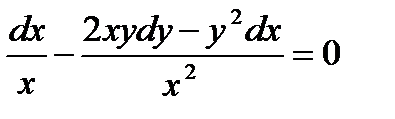 , откуда
, откуда 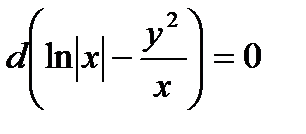 и общий интеграл данного уравнения
и общий интеграл данного уравнения
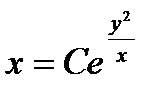
2. Аналогично, если 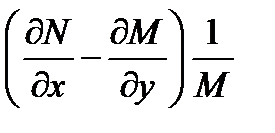 есть функция только y, то уравнение (1) имеет интегрирующий множитель
есть функция только y, то уравнение (1) имеет интегрирующий множитель 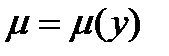 , зависящий только от y.
, зависящий только от y.
Интеграл уравнения (1)
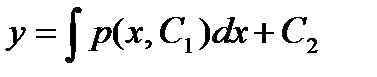
Пример 8.1. Решить уравнение
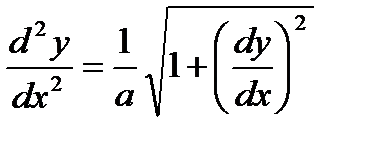
Решение. Положим 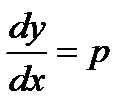 , тогда
, тогда
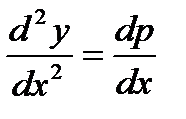
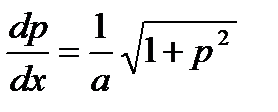
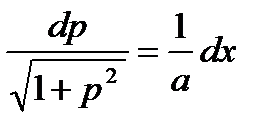
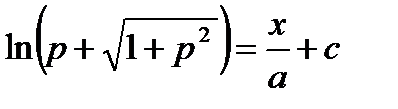
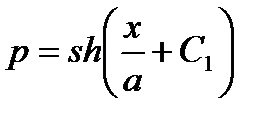
т.к. 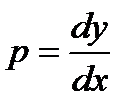 , интеграл последнее соотношение, получим уравнение цепной линии
, интеграл последнее соотношение, получим уравнение цепной линии
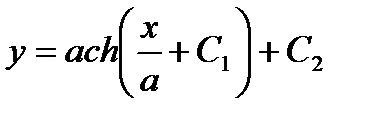
Найдём частное решение, удовлетворяющее начальным условиям
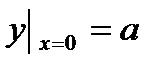 ,
, 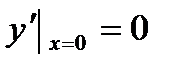
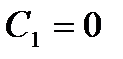 ,
, 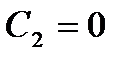 ,
, 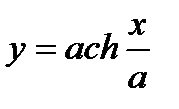
Замечание. Аналогично можно проинтегрировать уравнение
2. Уравнение вида
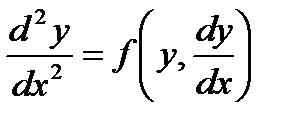 (2)
(2)
не содержит явным образом независимой переменной x.
Для его решения снова положим
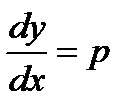 (3)
(3)
но теперь будем считать p функцией от y (а не от x, как прежде). Тогда
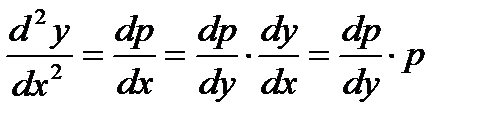
Подставляя выражение 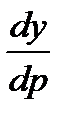 и
и 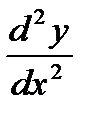 в уравнение (2), получим уравнение 1-ого порядка
в уравнение (2), получим уравнение 1-ого порядка 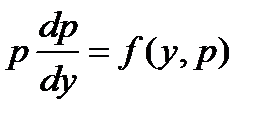
Интегрируя его, найдём p, как функцию y и производной постоянной 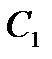 :
:
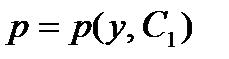
Подставляя это значение в соотношение (3), получим
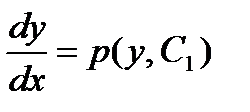
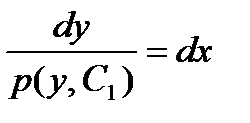
Интегрируя это уравнение, получим общий интеграл исходного уравнения
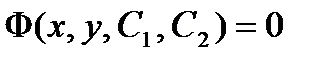
Пример 8.2. Найти общий интеграл уравнения
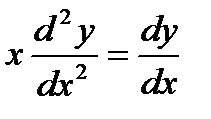
Решение. Пусть 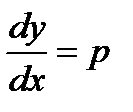 , тогда
, тогда 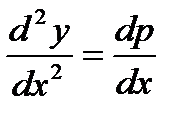
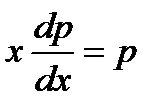
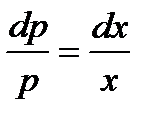
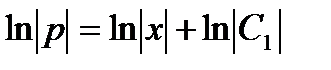
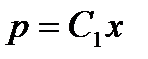
Возвратимся к переменной y: 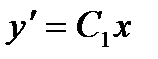
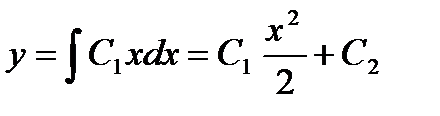




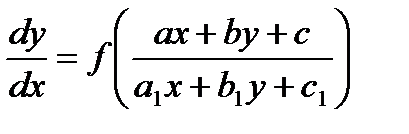
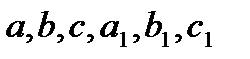 — постоянные
— постоянные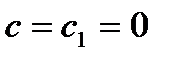 , то уравнение является однородным. Если хотя бы одно из чисел
, то уравнение является однородным. Если хотя бы одно из чисел 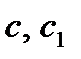 отлично от нуля, то следует различать два случая.
отлично от нуля, то следует различать два случая.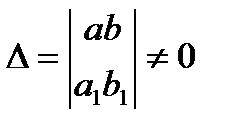
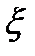 и
и  по формулам
по формулам 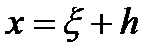 ,
, 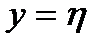 приведем уравнение к виду
приведем уравнение к виду 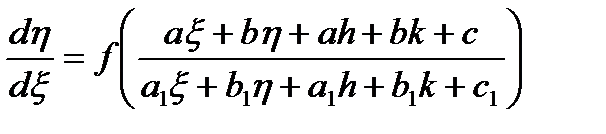
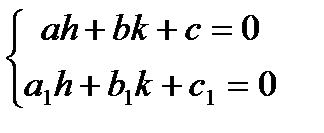
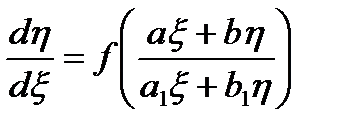 найдя его общий интеграл и заменив
найдя его общий интеграл и заменив 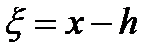 ,
, 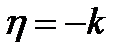 получаем общий интеграл уравнения
получаем общий интеграл уравнения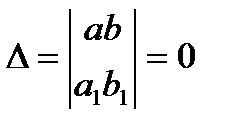 и уравнение имеет вид
и уравнение имеет вид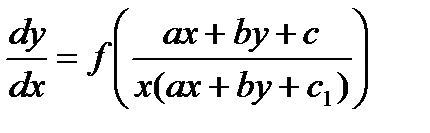
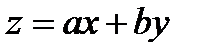 приводит его к уравнению с разделяющими переменными.
приводит его к уравнению с разделяющими переменными.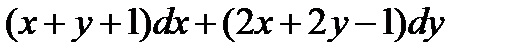
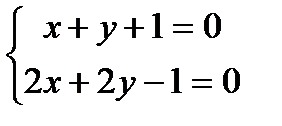 несовместна. В том случае метод, применённый в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку
несовместна. В том случае метод, применённый в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку 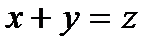 ,
, 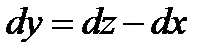 . Уравнение примет вид
. Уравнение примет вид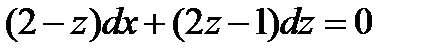
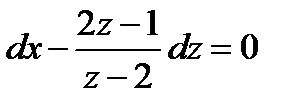 ,
, 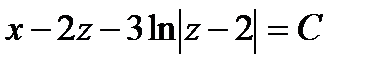
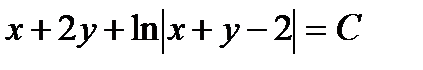
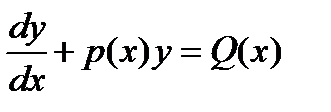 . (1)
. (1)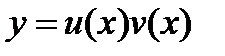
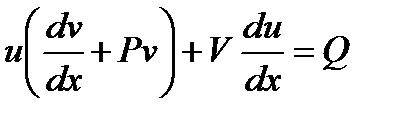
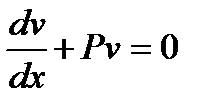 найдём
найдём 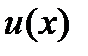 , и следовательно и решение
, и следовательно и решение 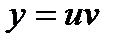
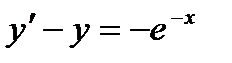 ,
, 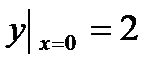
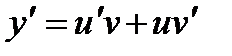 . Подставляя выражения для
. Подставляя выражения для 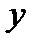 и
и 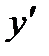 в данное уравнение, будем иметь
в данное уравнение, будем иметь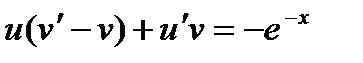
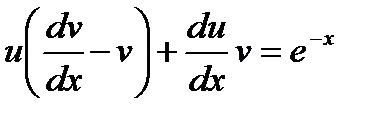
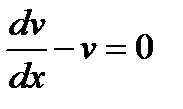 ,
, 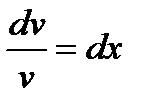 ,
, 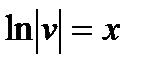 ,
, 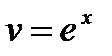
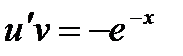 ,
,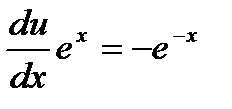 ,
, 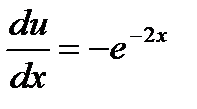 ,
, 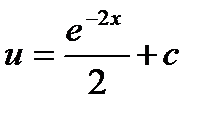
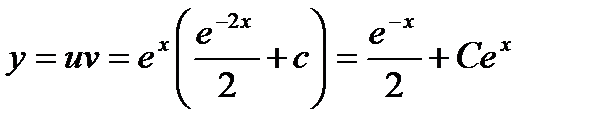
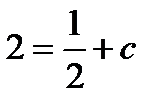 ,
, 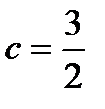 ;
;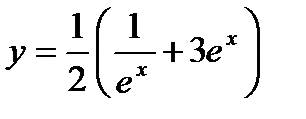 .
.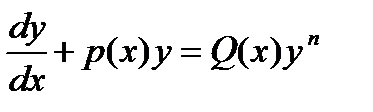 , где
, где 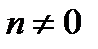
 уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.
уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.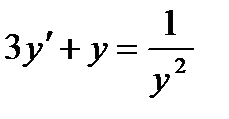
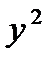
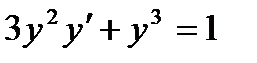
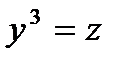 , тогда
, тогда 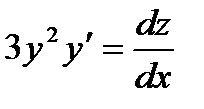 , подставим в уравнение
, подставим в уравнение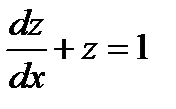
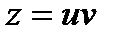 ,
, 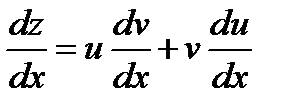
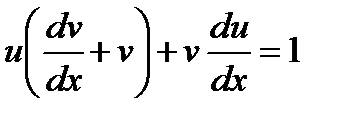 ,
, 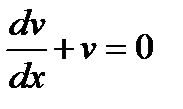 ,
, 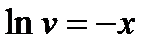 ,
, 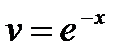
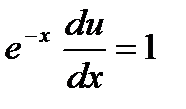 ,
, 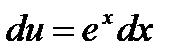 ,
, 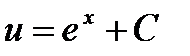
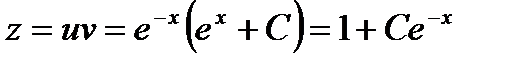
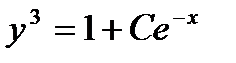
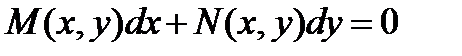 (1) называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции
(1) называется уравнением в полных дифференциалах, если его левая часть представляет полный дифференциал некоторой функции 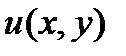 т.е.
т.е.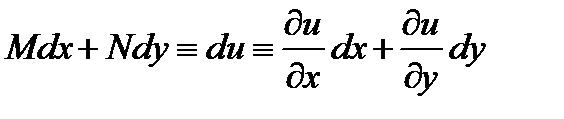
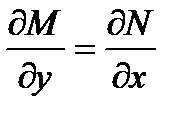
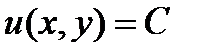
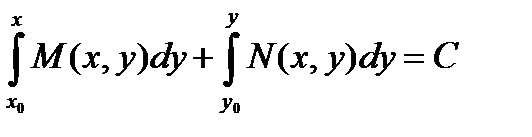
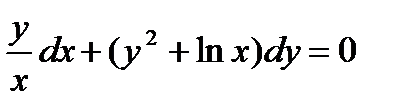
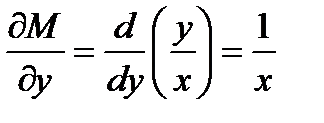 ,
, 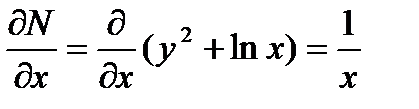 , так что
, так что 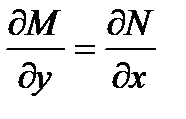
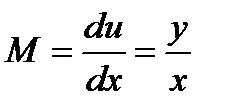 ,
, 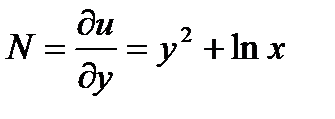 , поэтому
, поэтому 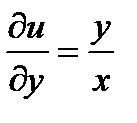 , проинтегрируем
, проинтегрируем 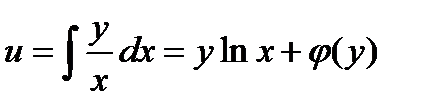
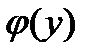 пока неопределённая функция.
пока неопределённая функция.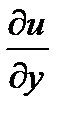 найденной функции
найденной функции 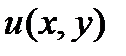 должна равняться
должна равняться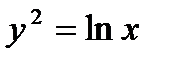 ,
,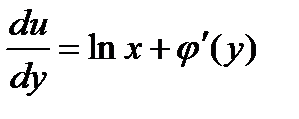 ,
,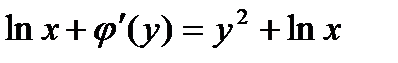
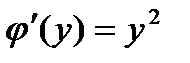
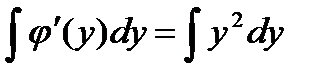
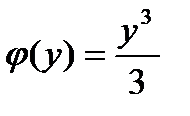
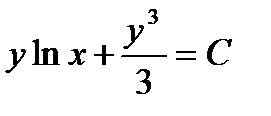
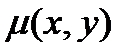 , после умножения на которую, левая часть (1) превращается в полный дифференциал
, после умножения на которую, левая часть (1) превращается в полный дифференциал 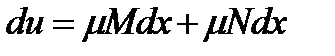 .
.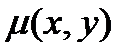 называется интегрирующим множителем из определения интегрирующего множителя
называется интегрирующим множителем из определения интегрирующего множителя 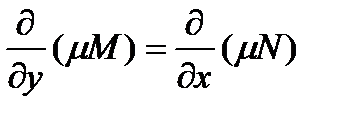 или
или 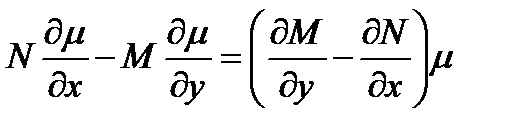
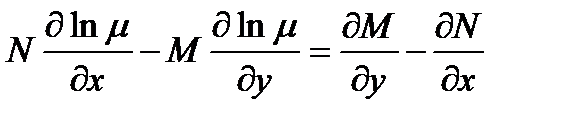 (2)
(2)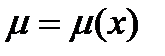 , то
, то 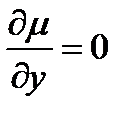 и уравнение (2) примет вид
и уравнение (2) примет вид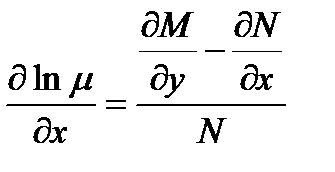 (3)
(3)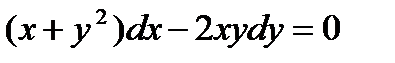
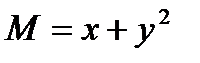 ,
, 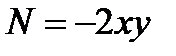 , имеем
, имеем 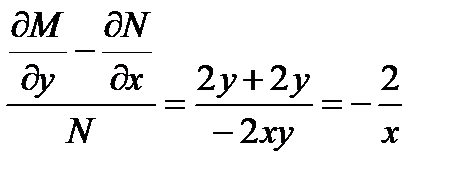 , следовательно
, следовательно 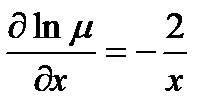 ,
, 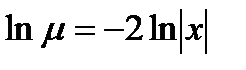 ,
, 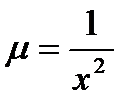
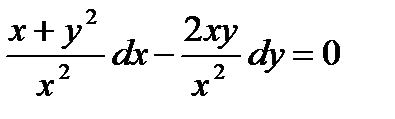 в полных дифференциалах
в полных дифференциалах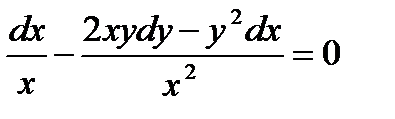 , откуда
, откуда 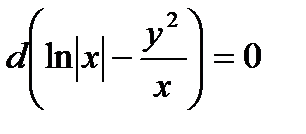 и общий интеграл данного уравнения
и общий интеграл данного уравнения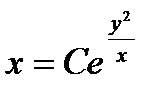
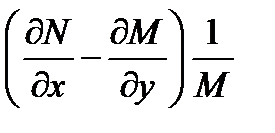 есть функция только y, то уравнение (1) имеет интегрирующий множитель
есть функция только y, то уравнение (1) имеет интегрирующий множитель 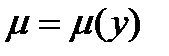 , зависящий только от y.
, зависящий только от y.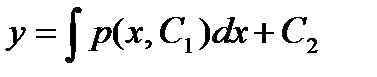
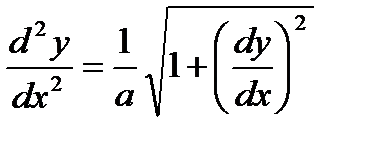
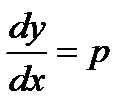 , тогда
, тогда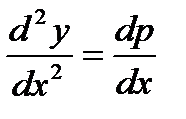
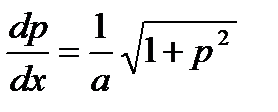
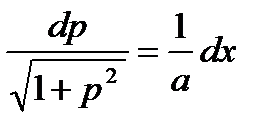
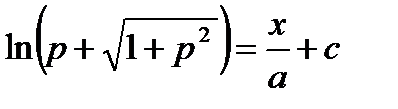
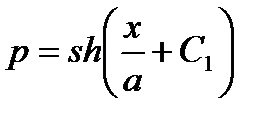
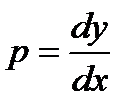 , интеграл последнее соотношение, получим уравнение цепной линии
, интеграл последнее соотношение, получим уравнение цепной линии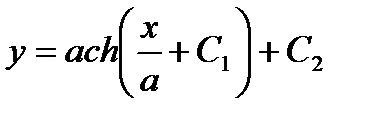
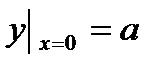 ,
, 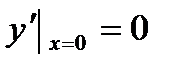
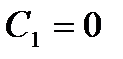 ,
, 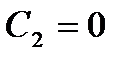 ,
, 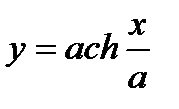
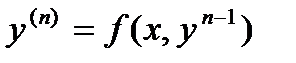
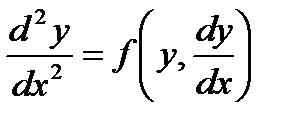 (2)
(2)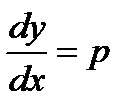 (3)
(3)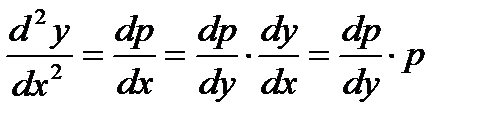
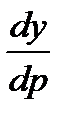 и
и 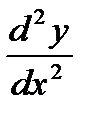 в уравнение (2), получим уравнение 1-ого порядка
в уравнение (2), получим уравнение 1-ого порядка 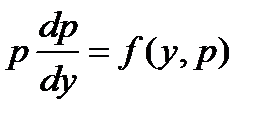
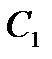 :
: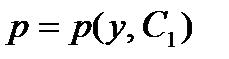
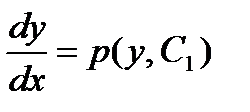
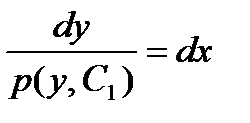
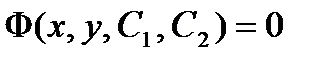
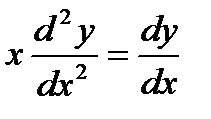
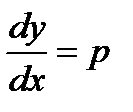 , тогда
, тогда