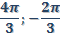Свойства степени с произвольным показателем.
a) Степень с натуральным показателем.
Определение:  , где n-любое натуральное число называется степенью с натуральным показателем.
, где n-любое натуральное число называется степенью с натуральным показателем.
 =a·a·a…·a
=a·a·a…·a
n-раз
 =2·2·2·2=4·4=16
=2·2·2·2=4·4=16
4 раза
a- основание степени
т-показатель степени
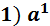 = a 5)
= a 5)  =
= 
 = 1 6)
= 1 6)  =
=  ·
· 
3)  ·
·  =
=  7)
7)  =
= 
4) 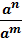 =
=  8)
8)  =
= 
б) Степень с рациональным показателем.
Определение: Под степенью с рациональным показателем  , где q
, где q  1 понимают
1 понимают  , т.е.
, т.е.  =
=  , a>0
, a>0  =
= 
Все свойства степени с натуральным показателем верны для степени с любым рациональным показателем и положительным основанием.
r и s –рациональные числа, т.е. числа вида  q
q  1
1
1)  = a 4)
= a 4) 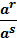 =
=  7)
7)  =
= 
2)  = 1 5)
= 1 5)  =
=  8)
8)  =
= 
3)  ·
·  =
= 
 =
=  ·
·  9)
9)  =
= 
Определение логарифма числа и его свойства. Натуральные и десятичные логарифмы.
Показательное уравнение вида 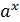 =b (при условии, что числа a и b положительны, где a
=b (при условии, что числа a и b положительны, где a  0; a
0; a  0 и b
0 и b  0) имеет решение, которое можно записать:
0) имеет решение, которое можно записать: 
 = b = b
| - Основное логарифмическое тождество.
|
Например,  = 7;
= 7; 
 ;
;  125 и т.д.
125 и т.д.
Определение: Логарифмом положительного числа b по положительному и отличному от единицы основанию a, называется показатель степени x, в которую нужно возвести число a, чтобы получить число b. Таким образом,  =x
=x
 b; a > 0; a < 0 и a
b; a > 0; a < 0 и a 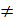 1
1
Операцию нахождение логарифма называют логарифмированием. Эта операция является обратной по отношению к операции возведение в степень соответствующим основаниям.
Возведение в степеньЛогарифмирование
 =25
=25  =2
=2
 =0,001
=0,001  =3
=3
 =ln3 =ln3
|
Определение: Логарифмом по основанию 10 называется десятичным логарифмом и обозначается символом lg (читается десятичный логарифм), т.е. вместо  пишут lg 5. Если в основании логарифма стоит число a = e
пишут lg 5. Если в основании логарифма стоит число a = e  2,71828… e
2,71828… e  2,7, то такой логарифм называется натуральным и обозначается символом:
2,7, то такой логарифм называется натуральным и обозначается символом:  (читается натуральный логарифм), т.е. вместо записи логарифм трёх по основанию e пишут
(читается натуральный логарифм), т.е. вместо записи логарифм трёх по основанию e пишут 
Особо выделим 3 формулы:
1) 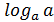 =1 (
=1 (  =1)
=1)
2) 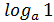 =0 (
=0 (  =0)
=0)
3) 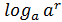 =r (
=r ( 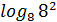 =2)
=2)
Свойства логарифмов.
Все свойства формулируются и доказываются только для положительных значений переменных, содержащихся под знаками логарифмов. Впрочем, два свойства доказательства не требуют, они представляют собой запись на математическом языке определения логарифма как показателя степени. Мы ими уже пользовались:
 = b = b
|
 = r = r
|
Теорема 1. Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:
Например, 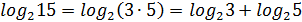 ;
;
 .
.
Доказательство: Введём следующие обозначения.
Подготовка к доказательству Перевод на более Доказательство
(введение новых переменных) простой язык
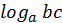 =x
=x  =bc
=bc  =
= 
 =y
=y  =b
=b  =
= 
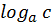 =z
=z  =c x=y+z
=c x=y+z
Доказать x=y+z
Теорема 2 .Если a,b,c-положительные числа, причём a  1, то справедливо равенство
1, то справедливо равенство
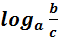 = = 
|
Краткая формулировка, которую удобнее использовать на практике: логарифм частного равен разности логарифмов делимого и делителя или логарифм дроби равен разности логарифмов числителя и знаменателя.
Например, 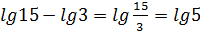
Доказательство:
Подготовка к доказательству Перевод на более Доказательство
(введение новых переменных) простой язык
 x
x 


 y
y  b
b 
 z
z  c x
c x  y-z
y-z
Доказать x 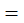 y-z
y-z
 r r 
|
Теорема 3 .Если a и b-положительные числа, причём a  1, то для любого числа r справедливо равенство
1, то для любого числа r справедливо равенство
Например, 
lg 
Краткая формулировка, которую удобнее использовать на практике: логарифм степени равен произведению показателя степени на логарифм основания степени.
Доказательство:
Подготовка к доказательству Перевод на более Доказательство
(введение новых переменных) простой язык
 x
x 


 y
y  b
b 
x 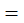 ry
ry
Доказать x=ry
3.Тригонометрические функции числового аргумента(определения, табличные значения).
Определение №1 : Если точка М числовой окружности соответствует числу t радиан, абсциссу точки М называют синусом числа t(cost),а ординату точки М называют синусом числа t.
x  cost cost
 sint sint
|
M(x;y)
t
Определение №2: Отношение синуса числа t к косинусу того же числа называется тангенсом числа t, т.е. tg t 
Определение №3 : Отношение косинуса t, к синусу t называется котангенсом, т.е. ctg t 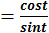
Каждому действительному числу t на числовой окружности можно поставить в соответствии определённое число cost (или sint, или tgt, или ctgt), таким образом, речь идёт о четырёх тригонометрических функциях числового аргумента, где t-любое действительное число.
Табличные значения
Тригонометрических функций

| 
| 
| 
| 
| 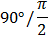
| 
| 
| 
|
| sint
| 0
| 
| 
| 
| 1
| 0
| -1
| 0
|
| cost
| 1
| 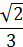
| 
| 
| 0
| -1
| 0
| 1
|
| tgt
| 0
| 
| 1
| 
| Не сущ.
| 0
| Не сущ.
| 0
|
| ctgt
| 0
| 
| 1
| 
| 0
| Не сущ.
| 0
| Не сущ.
|
Арккосинус
Определение: Арккосинусом числа a (arccos a), где a  , называется такое число t на окружности (или угол) t
, называется такое число t на окружности (или угол) t  , косинус которого равен числу a
, косинус которого равен числу a
arccosa  t t
|
cos t  a
a
0 
Свойство арккосинуса:
arccos(-a)  -arccosa -arccosa
|
Функция не является ни четной, ни нечётной
Арксинус
Определение: Арксинусом числа a(arcsina), где -1  a
a  1, называется такое число t на окружности (или угол) t
1, называется такое число t на окружности (или угол) t  синус которого равен числу a
sin t
синус которого равен числу a
sin t  a
a

Свойство арксинуса:
arcsin(-a)=  arcsina arcsina
|
Функция не чётная
Арктангенс
Определение: Арктангенсом числа a (arctga), где a-любое действительное число на линии tg, называется такое число t на окружности из интервала  , тангенс которого равен числу a
, тангенс которого равен числу a
tg t  a
a

Свойство арктангенса:
arctg(-a)=  arctga arctga
|
Функция не чётная
Арккотангенс
Определение: Арккотангенсом числа a (arcctga), где a-любое действительное число, называется такое число t на окружности (или угол), котангенс которого равен числу a
arcctga  t t
|
ctg t  a
a
0<t< 
t  (0;
(0;  )
)
Свойство арккотангенса:
arcctg(-a)=  -arcctga -arcctga
|
Функция не является не чётной, ни не чётной
Табличные значения арккотангенса
Вывод формул обратных
Тригонометрических функций.
arccos(-a) 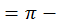 arccosa
arcsin(-a) arccosa
arcsin(-a)  arcsina
arctg(-a) arcsina
arctg(-a)  arctga
arcctg(-a) arctga
arcctg(-a) 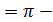 arcctga arcctga
|
Основные тригонометрические формулы (зависимость между тригонометрическими функциями одного и того же аргумента, суммы и разности аргументов, двойного аргументов, понижения степени, суммы и разности тригонометрических функций, формулы приведения).
Формулы двойного аргумента.
(1) sin 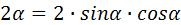
|
(2) cos 
|
(3) tg2 
|
Формулы суммы и разности
тригонометрических функций.
Формулы сложения тригонометрических функций позволяют преобразовывать сумму и разность функций в произведение этих функций.
cos 
|
sin 
|
sin 
|
cos 
|
Формулы приведения.
Значения тригонометрических функций острых углов вычисляют по таблице, либо по модели числовая окружность.
Значения функций любых углов можно вычислить с помощью формул приведения к острому углу. Формул приведения много, поэтому лучше запомнить правило написаний этих формул, а не сами формулы.
ПРАВИЛО НАПИСАНИЯ ФОРМУЛ ПРИВЕДЕНИЯ:
1) Если под знаком тригонометрической функции содержится (  , или (
, или (  , то наименование функции нужно изменить на родственное (sin cos; tg ctg)
, то наименование функции нужно изменить на родственное (sin cos; tg ctg)
2) Если под знаком тригонометрической функции содержится (  то наименование тригонометрической функции менять не нужно.
то наименование тригонометрической функции менять не нужно.
3)Перед полученной функцией от аргумента t нужно поставить тот знак, которая имела бы преобразуемая функция при условии, что
0<t<  (0
(0  <
<  <90
<90 
1) sin (  17) tg (
17) tg ( 
2) sin (  18) tg (
18) tg ( 
3) sin (  19) tg (
19) tg ( 
4) sin  20) tg
20) tg 
5) sin (  21) tg (
21) tg ( 
6) sin  22) tg
22) tg 
7) sin 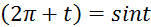 23) tg
23) tg 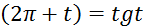
8) sin 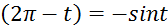 24) tg
24) tg 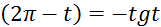
9) cos (  25) ctg (
25) ctg ( 
10) cos (  26) ctg (
26) ctg ( 
11) cos (  27) ctg (
27) ctg ( 
12) cos  28) ctg
28) ctg 
13) cos ( 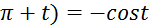 29) ctg (
29) ctg ( 
14) cos  30) ctg
30) ctg 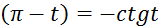
15) cos 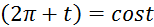 31) ctg
31) ctg 
16) cos  32) ctg
32) ctg 
6.Решение уравнения sinx=a.
(вывод формул корней уравнения sint=a)
Если  то уравнение sin =a имеет корни, если
то уравнение sin =a имеет корни, если  то уравнение корней не имеет. Например:
то уравнение корней не имеет. Например:
sint = 2
2  нет корней
нет корней
sint = -1,8
|-1,8|=1,8  нет корней
нет корней
Вывод формул корней

 0;
0; 
t= arcsina+  k k
|
Вывод: Уравнение sint  a имеет две серии решений: (1)
a имеет две серии решений: (1)
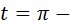 arcsina arcsina
|
(2)
Эти две формулы объединим в одну:
t  k
k
(1) t 
|
при любом k
(2) t 
|
t =   k k
|
Формула корней уравнения sin t=a
Свойство:
 (1) формула
(1) формула
 (2) формула
(2) формула
Три частных случая:
1) sint  t
t 
2) sint  t
t 
3) sin  t
t 
Например, Решить уравнение
sint 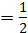
t 
t 
7.Решение уравнения cosx=a
(Вывод формул корней уравнения cost=a)
Решить тригонометрическое уравнение cost=a, значит найти все числа t на окружности cos, которых равен числу a.
y

a 
x |a|  1
1
Если |a|  то тригонометрическое уравнение cos t=a имеет корни.
то тригонометрическое уравнение cos t=a имеет корни.
Если |a|  то тригонометрическое уравнение cos t=a не имеет решений.
то тригонометрическое уравнение cos t=a не имеет решений.
cos t  1,5
1,5  нет корней
нет корней
cos t  |
|  |
|  нет корней
нет корней
y Вывод формул корней

(k 
x
 1
1

Вывод: Уравнение cost=a имеет две серии решений:
t=  k
k
t=  (k
(k  , которые можно объединить в одну формулу
, которые можно объединить в одну формулу
Формула корней уравнения cost=a
Свойство:
Но в трёх частных случаев предпочитают пользоваться не формулой корней, а более простыми соотношениями:
1) cos t  t
t 
2) cos t  t
t 
3) cos t 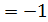 t
t 
Например, Решить уравнение
cos t 
|a| 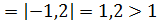 нет корней
нет корней
8.Решение уравнения tgx=a.
(Вывод формулы корней уравненияtgt=a),
y где a-любое действительное число на линии tg.
tg
a +
t=arctga
x

Формула корней уравнения tgt  a
a:
Свойство:
Частных случаев нет!
Например, Решить уравнение:
tgt=1,5
t=arctg1,5 
9.Решение уравнения ctg=a.
(Вывод формулы корней уравнения ctgt=a),
Где a-любое действительное число на линии ctg
y
ctgt 0 a ctgt
arcctga
x
arcctga+ 
t 
|
Формула корней уравнения ctgt=a
arcctg(-a) 
|
Свойство:
Например, Решить уравнение:
ctgt 
t 
tgt
0
 ctgt
ctgt  1
1  ctgt
ctgt

 0;2
0;2 


Свойства степени с произвольным показателем.
a) Степень с натуральным показателем.
Определение:  , где n-любое натуральное число называется степенью с натуральным показателем.
, где n-любое натуральное число называется степенью с натуральным показателем.
 =a·a·a…·a
=a·a·a…·a
n-раз
 =2·2·2·2=4·4=16
=2·2·2·2=4·4=16
4 раза
a- основание степени
т-показатель степени
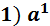 = a 5)
= a 5)  =
= 
 = 1 6)
= 1 6)  =
=  ·
· 
3)  ·
·  =
=  7)
7)  =
= 
4) 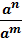 =
=  8)
8)  =
= 
б) Степень с рациональным показателем.
Определение: Под степенью с рациональным показателем  , где q
, где q  1 понимают
1 понимают  , т.е.
, т.е.  =
=  , a>0
, a>0  =
= 
Все свойства степени с натуральным показателем верны для степени с любым рациональным показателем и положительным основанием.
r и s –рациональные числа, т.е. числа вида  q
q  1
1
1)  = a 4)
= a 4) 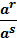 =
=  7)
7)  =
= 
2)  = 1 5)
= 1 5)  =
=  8)
8)  =
= 
3)  ·
·  =
= 
 =
=  ·
·  9)
9)  =
= 
|
|
|



 , где n-любое натуральное число называется степенью с натуральным показателем.
, где n-любое натуральное число называется степенью с натуральным показателем. =2·2·2·2=4·4=16
=2·2·2·2=4·4=16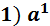 = a 5)
= a 5)  =
= 
 = 1 6)
= 1 6)  =
=  ·
· 
 =
=  7)
7)  =
= 
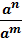 =
=  8)
8)  =
= 
 , где q
, где q  1 понимают
1 понимают  , т.е.
, т.е.  =
= 
 q
q  = a 4)
= a 4) 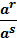 =
=  7)
7)  =
= 
 = 1 5)
= 1 5)  =
=  8)
8)  =
= 
 ·
·  =
= 
 =
=  ·
·  9)
9)  =
= 
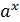 =b (при условии, что числа a и b положительны, где a
=b (при условии, что числа a и b положительны, где a  0; a
0; a 
 = b
= b
 = 7;
= 7; 
 ;
;  125 и т.д.
125 и т.д. =x
=x b; a > 0; a < 0 и a
b; a > 0; a < 0 и a 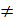 1
1 =25
=25  =2
=2 =0,001
=0,001  =3
=3 =ln3
=ln3
 пишут lg 5. Если в основании логарифма стоит число a = e
пишут lg 5. Если в основании логарифма стоит число a = e  2,71828… e
2,71828… e  (читается натуральный логарифм), т.е. вместо записи логарифм трёх по основанию e пишут
(читается натуральный логарифм), т.е. вместо записи логарифм трёх по основанию e пишут 
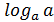 =1 (
=1 (  =1)
=1)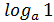 =0 (
=0 (  =0)
=0)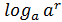 =r (
=r ( 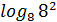 =2)
=2) = b
= b
 = r
= r
 =
=  +
+ 
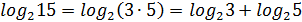 ;
; .
.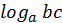 =x
=x  =bc
=bc 
 =y
=y  =b
=b 
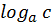 =z
=z  =c x=y+z
=c x=y+z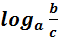 =
= 
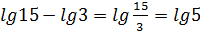
 x
x 


 y
y  b
b 
 z
z  c x
c x  y-z
y-z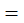 y-z
y-z r
r 




 y
y  b
b 
 cost
cost
 sint
sint
 cost
cost 
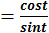





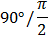






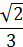


 , называется такое число t на окружности (или угол) t
, называется такое число t на окружности (или угол) t  , косинус которого равен числу a
, косинус которого равен числу a
 t
t

 -arccosa
-arccosa
 синус которого равен числу a
синус которого равен числу a

 arcsina
arcsina












 , тангенс которого равен числу a
, тангенс которого равен числу a
 t
t

 (0;
(0; 







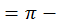 arccosa
arcsin(-a)
arccosa
arcsin(-a)  arcsina
arctg(-a)
arcsina
arctg(-a) 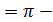 arcctga
arcctga
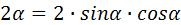






 , или (
, или (  , то наименование функции нужно изменить на родственное (sin cos; tg ctg)
, то наименование функции нужно изменить на родственное (sin cos; tg ctg) то наименование тригонометрической функции менять не нужно.
то наименование тригонометрической функции менять не нужно. (0
(0  <
<  <90
<90 
 17) tg (
17) tg ( 
 18) tg (
18) tg ( 
 19) tg (
19) tg ( 
 20) tg
20) tg 
 21) tg (
21) tg ( 
 22) tg
22) tg 
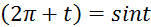 23) tg
23) tg 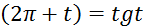
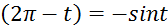 24) tg
24) tg 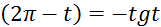
 25) ctg (
25) ctg ( 
 26) ctg (
26) ctg ( 
 27) ctg (
27) ctg ( 
 28) ctg
28) ctg 
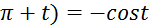 29) ctg (
29) ctg ( 
 30) ctg
30) ctg 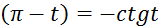
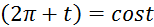 31) ctg
31) ctg 
 32) ctg
32) ctg 
 то уравнение sin =a имеет корни, если
то уравнение sin =a имеет корни, если  то уравнение корней не имеет. Например:
то уравнение корней не имеет. Например: нет корней
нет корней

 k
k
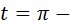 arcsina
arcsina
 k
k


 k
k

 (1) формула
(1) формула (2) формула
(2) формула t
t 
 t
t 
 t
t 
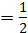




 1
1 то тригонометрическое уравнение cos t=a имеет корни.
то тригонометрическое уравнение cos t=a имеет корни. то тригонометрическое уравнение cos t=a не имеет решений.
то тригонометрическое уравнение cos t=a не имеет решений. 1,5
1,5  |
|  |
|  нет корней
нет корней


 k
k (k
(k 



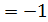 t
t 

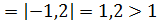 нет корней
нет корней


 a:
a:










 ctgt
ctgt  1
1 









 0;2
0;2