Существуют три характерных признака заряда. Во-первых, заряды могут быть положительными и отрицательными. Во-вторых, величина заряда не зависит от условий его определения. В частности, заряд не меняется при движении с релятивистскими скоростями. В-третьих, в изолированной системе заряды сохраняются (закон сохранения зарядов).
Взаимодействие зарядов осуществляется через поле. Это ставит задачи описания силового и энергетического проявления электрического поля при наличии или отсутствии как связанных, так и свободных, зарядов.
Взаимодействие зарядов. Закон Кулона.
Сила взаимодействия так называемых точечных зарядов определяется законом Кулона. Точечный заряд – заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями от этого тела до других тел, несущих электрический заряд.
Основное предположение Кулона: при соприкосновении двух одинаковых заряженных шариков заряд распределяется между обоими шариками поровну. Это, собственно, был способ дозировки зарядов в установке.
Результат измерений Кулона: сила взаимодействия двух точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними.
F=k(q1q2/r^2)
В случае одноименных зарядов сила, вычисленная по формуле (1), оказывается положительной (что соответствует отталкиванию между зарядами). В случае разноименных зарядов сила отрицательна (притяжение зарядов друг к другу
Сила взаимодействия между зарядами, сосредоточенными на телах конечных размеров определяется, если разбить каждый из зарядов на такие малые заряды d q, чтобы их можно было считать точечными.
Напряженность поля.
Пусть поле создается точечным зарядом q. На точечный пробный заряда q в точке, определяемой радиус-вектором r (рис.3), действует сила
F=q(1/4pi(e0)*(q/r^2)*(r/r)
Это отношение однозначно характеризует электрическое поле: E=F/q
Векторную величину E называют напряженностью электрического поля в в той точке, в которой пробный заряд испытывает действие силы f. Напряженность электрического поля численно равна силе, действующей на единичный точечный заряд, находящийся в данной точке поля. Векторы Е и f параллельны при условии положительного заряда q пp.
Таким образом, напряженность поля точечного заряда пропорциональна величине заряда q и обратно пропорциональна квадрату расстояния r от заряда до данной точки поля: E=(1/4pi(e0))(q/r^2)*(r/r)
Единица напряженности электрического поля – напряженность, при которой на заряд, равный 1 Кл действует сила равная 1Н. Эта единица напряженности электрического поля называется вольт на метр и обозначается в/м.
Сила, действующая на пробный заряд, равна f = q пp × E.
Суперпозиция полей.
Опытный факт: сила, с которой система зарядов действует на некоторый не входящий в систему заряд, равна векторной сумме сил, с которыми действует на данный заряд каждый из зарядов системы в отдельности. Следствие: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности: E=E1+E2+…En
Это утверждение называется принципом суперпозиции (наложения) электрических полей. Принцип суперпозиции позволяет вычислить напряженность поля любой системы зарядов, представимых в виде малых величин dq (точечных зарядов).
такому же закону, как и у поля точечного заряда.
Поле диполя.
Напряженность поля электрического диполя.
Посмотреть по Иродову. Электрический диполь – система двух одинаковых по величине разноименных точечных зарядов: + q и – q. Расстояние между ними значительно меньше, чем расстояние до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя.
напряженность поля диполя в произвольной точке определяется формулой
E=(1/4h(e0))*(p/r^3)(кор(1+3сos^2альфа)
где a – угол между осью диполя и направлением на данную точку
Линии напряженности.
Поток вектора напряженности.
Электрическое поле задается указанием для каждой точки величины и направления вектора Е. Совокупность этих векторов образует поле вектора напряженности электрического поля. В гидродинамике поле, например, вектора скорости, можно представить очень наглядно с помощью линий тока. Аналогично электрическое поле можно описать с помощью линий напряженности, которые называются сокращенно линиями Е.
Линию Е удобно выбрать так, чтобы касательная к ней в каждой точке была параллельна вектору Е. При этом густоту линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, можно приравнять численному значению модуля вектора Е. Тогда по картине линий напряженности можно судить о направлении и величине вектора Е в разных точках пространства (рис. 7).
 Рис. 7.
Рис. 7.
|  Рис. 8. Рис. 8.
|
Линии Е точечного заряда – радиальные прямые, направленные от заряда, если он положителен, и к заряду, если он отрицателен (рис. 8).
Можно доказать, что линии одним концом опираются на заряд, другим уходят в бесконечность.
В соответствии с приведенными выше соглашениями полное число линий N, пересекающих сферическую поверхность радиуса r, равно произведению густоты линий на поверхность сферы 4 π r 2. Густота линий по условию численно равна
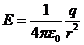
Следовательно, N численно равно

т. е. число линий на любом расстоянии от заряда одно и то же. Следовательно, линии нигде, кроме заряда, не начинаются и не заканчиваются. Это свойство линий Е является общим для всех электростатических полей, создаваемых любой системой неподвижных зарядов: линии напряженности могут начинаться или заканчиваться лишь на зарядах, либо уходить в бесконечность. Поскольку густота линий Е выбирается равной численному значению Е, количество линий, пронизывающих площадку d S, перпендикулярную к вектору Е, численно равно Е d S. Если нормаль площадки d S ориентирована под углом a к Е, количество линий, пронизывающих площадку, численно равно:
 , (8)
, (8)
где E n – составляющая вектора Е по направлению нормали к площадке (нормальная составляющая). Отсюда количество линий Е, пронизывающих произвольную поверхность, оказывается равным:
 (9)
(9)
Определение. Если имеется поле некоторого вектора А, то выражение
 (10)
(10)
где А n – нормальная составляющая вектора А по направлению к d S, называется потоком вектора А через поверхность S.
В зависимости от природы вектора А выражение (10) имеет различный физический смысл. Например, поток вектора плотности потока энергии равен потоку энергии через соответствующую поверхность. Поток вектора скорости жидкости
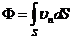
дает объем жидкости, протекающей в единицу времени через поверхность S.
Таким образом, поток вектора Е
 (11)
(11)
численно равен количеству линий Е, пронизывающих поверхность S.
Поток (11) есть алгебраическая величина. Знак его зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении Ф.
Изменение направления нормали на противоположное изменяет знак у E n, следовательно, и знак у потока Ф. В случае замкнутых поверхностей принято вычислять поток, выходящий
из охватываемой поверхностью области наружу. Поэтому под нормалью к d S в дальнейшем будет всегда подразумеваться обращенная наружу, т. е. внешняя, нормаль. В тех местах, где вектор Е направлен наружу (т. е. линия Е выходит из объема, охватываемого поверхностью), Е n и соответственно d Ф будут положительны; в тех же местах, где вектор Е направлен внутрь (т. е. линия Е входит в объем, охватываемый поверхностью), Е n и d Ф будут отрицательны (рис.9).
Теорема Гаусса
Окружающую точечный заряд q сферическую поверхность любого радиуса r пересекает 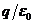 линий Е. То есть, из точечного заряда выходит (либо к нему сходится)
линий Е. То есть, из точечного заряда выходит (либо к нему сходится) 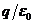 линий. В соответствии с (9) поток вектора Е через некоторую поверхность численно равен количеству линий Е, пересекающих эту поверхность. Следовательно, поток вектора Е через охватывающую заряд сферическую поверхность равен
линий. В соответствии с (9) поток вектора Е через некоторую поверхность численно равен количеству линий Е, пересекающих эту поверхность. Следовательно, поток вектора Е через охватывающую заряд сферическую поверхность равен 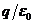 . Знак потока совпадает со знаком заряда.
. Знак потока совпадает со знаком заряда.
Независимость потока от поверхности. Поток вектора Е равен 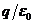 для поверхности любой другой формы, если она замкнута и заключает внутри себя точечный заряд q,. Для поверхности, не имеющей «морщин» (рис. 10,а), это утверждение очевидно. Действительно, такая поверхность, как и поверхность сферы, пересекается каждой линией Е только один раз.
для поверхности любой другой формы, если она замкнута и заключает внутри себя точечный заряд q,. Для поверхности, не имеющей «морщин» (рис. 10,а), это утверждение очевидно. Действительно, такая поверхность, как и поверхность сферы, пересекается каждой линией Е только один раз.
Поэтому число пересечений равно количеству линий, выходящих из заряда, т. е. 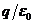 . При вычислении потока через поверхность с «морщинами» (на рис. 10,6 показана только одна из
. При вычислении потока через поверхность с «морщинами» (на рис. 10,6 показана только одна из 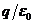 линий Е) нужно учесть, что число пересечений данной линии с поверхностью может быть в рассматриваемом случае только нечетным, причем эти пересечения будут вносить в общий поток попеременно то положительный, то отрицательный вклад. То есть, сколько бы раз данная линия не пересекала поверхность, результирующий вклад в поток будет равен либо плюс единице (для линии, выходящей в конечном счете наружу), либо минус единице (для линии, входящей внутрь). Таким образом, какова бы ни была форма замкнутой поверхности, охватывающей точечный заряд q, поток вектора Е сквозь эту поверхность оказывается равным
линий Е) нужно учесть, что число пересечений данной линии с поверхностью может быть в рассматриваемом случае только нечетным, причем эти пересечения будут вносить в общий поток попеременно то положительный, то отрицательный вклад. То есть, сколько бы раз данная линия не пересекала поверхность, результирующий вклад в поток будет равен либо плюс единице (для линии, выходящей в конечном счете наружу), либо минус единице (для линии, входящей внутрь). Таким образом, какова бы ни была форма замкнутой поверхности, охватывающей точечный заряд q, поток вектора Е сквозь эту поверхность оказывается равным 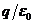 .
.
Пусть внутри некоторой замкнутой поверхности заключено несколько точечных зарядов произвольных знаков: q 1, q 2 и т. д. Поток вектора Е по определению равен
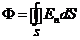 (12)
(12)
(кружок у знака интеграла указывает на то, что интегрирование производится по замкнутой поверхности). В силу принципа суперпозиции полей
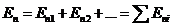 (13)
(13)
Подстановка (13) в выражение для потока дает

где  – нормальная составляющая напряженности поля, создаваемого i-м зарядом в отдельности. Последняя перестановка операции суммирования и интегрирования возможна, так как i относится к нумерации зарядов, интегрирование ведется по произвольной поверхности.
– нормальная составляющая напряженности поля, создаваемого i-м зарядом в отдельности. Последняя перестановка операции суммирования и интегрирования возможна, так как i относится к нумерации зарядов, интегрирование ведется по произвольной поверхности.
Выше было показано:
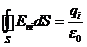
Следовательно,
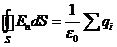 (14)
(14)
Это утверждение носит название теоремы Гаусса. Теорема может быть сформулирована следующим образом: поток вектора напряженности электрического поля через замкнутую
 Рис. 11.
Рис. 11.
|
поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e 0.
В частности. Если внутри поверхности заряды отсутствуют, поток равен нулю. В этом случае напряженность поля создавается зарядами, расположенными вне поверхности. Каждая линия напряженности пересекает поверхность четное число раз, выходя наружу столько же раз, сколько и входя внутрь (рис. 11). В итоге вклад, вносимый в поток каждой из линий, будет равен нулю. Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, теорема Гаусса должна быть записана следующим образом:
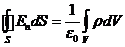 (15)
(15)
где интеграл справа берется по объему V, охватываемому поверхностью S.
6. Напряженность для различных конфигураций источников поля.
В случае удачной симметрии распределения зарядов теорема Гаусса позволяет найти напряженность поля гораздо проще, чем с использованием формулы для напряженности поля точечного заряда и принципа суперпозиции полей.
Определения.
Объемная плотность заряда аналогична обычной плотности: p=lim(dq/dV)
где d q – заряд, заключенный внутри малого объема dV.
Поверхностная плотность заряда: сигма=lim(dq/dS)
где D q – заряд, находящийся на отрезке цилиндрического тела, имеющем длину D l
Пользуясь теоремой Гаусса можно получить значения напряженностей для ряда часто используемых случаев распределения зарядов.
1. Поле бесконечной однородно заряженной плоскости. Плоскость заряжена с постоянной поверхностной плотностью (сигма). Из соображений симметрии следует, что Е в любой точке поля перпендикулярна к плоскости. В самом деле, поскольку плоскость бесконечна и заряжена однородно (т. е. с постоянной плотностью), нет никаких оснований к тому, чтобы сила, действующая на пробный заряд, отклонялась в какую-либо сторону от
нормали к плоскости.
Очевидно также, что в симметричных относительно плоскости точках Е одинакова по величине и противоположна по направлению.
откуда E=сигма/2(e0)
Таким образом, на любом расстоянии от плоскости напряженность одинакова по величине.
2. Поле двух разноименно заряженных плоскостей.
Поле двух параллельных бесконечных плоскостей, заряженных разноименно с одинаковой поверхностной плотностью сигма, определяется суперпозицией полей, создаваемых каждой из плоскостей в отдельности. В области между плоскостями (рис. 15) складываемые поля имеют одинаковое направление, так что результирующая напряженность равна E=сигма/e0
Вне объема, ограниченного плоскостями, складываемые поля имеют противоположные направления, так что результирующая напряженность равна нулю.
3. Поле бесконечного заряженного цилиндра.
Имеется бесконечная цилиндрическая поверхность радиуса R, заряженная с постоянной поверхностной плотностью сигма. Симметрия задачи подсказывает, что напряженность поля в любой точке направлена перпендикулярно к оси цилиндра, а величина напряженности определяется только расстоянием r от оси цилиндра. При этом на одинаковых расстояниях от центра цилиндра напряженность одинакова. E=сигма/e0
4. Поле заряженной сферической поверхности. Поле сферической поверхности радиуса R, заряженной с постоянной поверхностной плотностью s, очевидно, характеризуется центральной симметрией. То есть направление вектора Е в любой точке проходит через центр сферы, а величина напряженности является функцией только расстояния r от центра сферы.
E=сигма/e0
5. Поле объемно заряженной сферы радиуса R, заряженной с постоянной объемной плотностью r. Как и в предыдущем случае, поле такой сферы обладает центральной симметрией. Понятно, что для поля вне сферы получается тот же результат [в том числе и формула (17)]. Однако для точек внутри сферы результат будет иным. Сферическая поверхность радиуса r < R заключает в себе заряд,
E=(1/4pi(e0))*(q/R^3)*(r)
Таким образом, внутри сферы напряженность поля растет линейно с расстоянием r от центра сферы. Вне сферы напряженность убывает по такому же закону, как и у поля точечного заряда.
7. Работа сил электростатического поля
Сила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Из механики известно, что центральное поле сил потенциально. То есть, работа действительно зависит лишь от начального и конечного положений этого заряда (от r 1 и r 2) и не зависит от траектории перемещения заряда q '. Следовательно, силы, действующие на заряд q ' в поле неподвижного заряда q, потенциальны.
Этот вывод распространяется на поле любой системы неподвижных зарядов. Сила 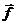 , действующая на точечный заряд q ', по принципу суперпозиции равна
, действующая на точечный заряд q ', по принципу суперпозиции равна
F=суммFi
где  – сила, обусловленная i-м зарядом системы источников поля. Работа равна сумме работ, совершаемых отдельными силами:
– сила, обусловленная i-м зарядом системы источников поля. Работа равна сумме работ, совершаемых отдельными силами:
A=суммAi
Каждое из слагаемых не зависит от пути. Следовательно, не зависит от пути и работа A.
Еще можно сказать о циркуляции и о том что циркуляция равна нуля в потенц поле
8. Потенциал
Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля.
Следовательно, работа (9.1) равна разности значений потенциальной энергии, которыми обладал заряд q ' в точках 1 и 2 поля заряда q:

Отсюда выражение для потенциальной энергии заряда q ' в поле заряда q
W=(1/4pi(e0))(qq/r)+C
Значение постоянной С выбирается таким, чтобы при удалении заряда на бесконечность (r = ¥) потенциальная энергия обращалась в нуль.
Величина фи=W/q
называется потенциалом поля в данной точке и является энергетической характеристикой электрического поля.
Потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. Следовательно потенциал поля точечного заряда равен: фи=(1/4pi(e0))(q/r)
Потенциал поля, создаваемого системой зарядов, равен сумме потенциалов, создаваемых каждым из зарядов в отдельности.
потенциальная энергия заряда q, находящегося в точке поля с потенциалом фи
W=qфи
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению величины заряда на разность потенциалов в начальной и конечной точках.
А=qфи
9. Связь между напряженностью электрического поля и потенциалом
Электрическое поле можно описать либо с помощью векторной величины Е, либо с помощью скалярной величины фи. Между этими величинами должна существовать связь. Так как Е пропорциональна силе, действующей на заряд, а фи – потенциальной энергии заряда, понятно, что эта связь должна быть аналогична связи между потенциальной энергией и силой.
Используя обозначение градиента, можно написать E = – gradфи
Напряженность электрического поля равна градиенту потенциала, взятому с обратным знаком.
Соотношение между напряженностью поля и потенциалом точечного заряда. Потенциал этого поля равен
Фи=
Проекция grad j на направление r равна
gradфи =(-1/4pi(e0))(q/r^2)
Разность потенциалов между двумя бесконечными разноименно заряженными плоскостями (однородное поле).
Фи1-фи2= E*d d-расстояние между пластинами конденастора
В частности, это выражение определяет связь разности потенциалов между пластинами конденсатора с напряженностью поля в конденсаторе. Расстояние между пластинами равно d.
Поле диполя.
Потенциал поля электрического диполя.
Посмотреть по Иродову. Электрический диполь – система двух одинаковых по величине разноименных точечных зарядов: + q и – q. Расстояние между ними значительно меньше, чем расстояние до тех точек, в которых определяется поле системы. Прямая, проходящая через оба заряда, называется осью диполя. Задача: найти напряженность поля на оси диполя, а также на прямой, проходящей через центр диполя и перпендикулярной к его оси (рис. 4).
Положение точек на этих прямых определим их расстоянием r от центра диполя.
Таким образом, Е ll = 2 Е ^. В общем случае рассмотрения напряженность поля диполя в произвольной точке определяется формулой
E=(1/4pi(e0)(p/r^3)(кор(1+3cos^2a)
где a – угол между осью диполя и направлением на данную



 Рис. 7.
Рис. 7.
 Рис. 8.
Рис. 8.
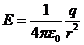

 , (8)
, (8) (9)
(9) (10)
(10)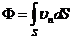
 (11)
(11)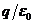 линий Е. То есть, из точечного заряда выходит (либо к нему сходится)
линий Е. То есть, из точечного заряда выходит (либо к нему сходится) 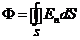 (12)
(12)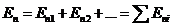 (13)
(13)
 – нормальная составляющая напряженности поля, создаваемого i-м зарядом в отдельности. Последняя перестановка операции суммирования и интегрирования возможна, так как i относится к нумерации зарядов, интегрирование ведется по произвольной поверхности.
– нормальная составляющая напряженности поля, создаваемого i-м зарядом в отдельности. Последняя перестановка операции суммирования и интегрирования возможна, так как i относится к нумерации зарядов, интегрирование ведется по произвольной поверхности.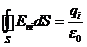
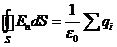 (14)
(14) Рис. 11.
Рис. 11.
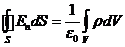 (15)
(15)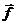 , действующая на точечный заряд q ', по принципу суперпозиции равна
, действующая на точечный заряд q ', по принципу суперпозиции равна – сила, обусловленная i-м зарядом системы источников поля. Работа равна сумме работ, совершаемых отдельными силами:
– сила, обусловленная i-м зарядом системы источников поля. Работа равна сумме работ, совершаемых отдельными силами:



