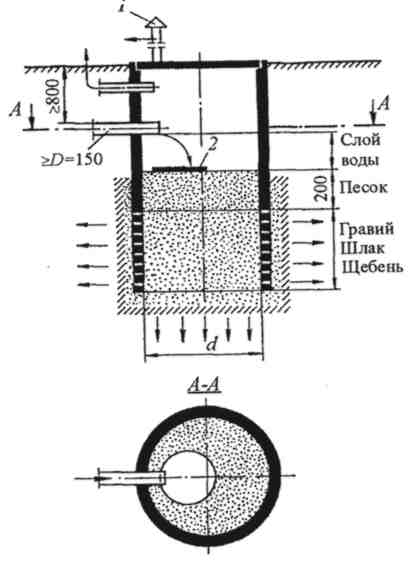
Понятие "уравнение линии" - есть основное понятие аналитической геометрии. Из него вытекают две основные задачи аналитической геометрии на плоскости:
А) Дана линия, рассматриваемая как множество точек. Составить алгебраическое уравнение этой линии.
Б) Дано уравнение некоторой линии. Изучить по этому уравнению её геометрические свойства: форму и расположение.
Линия называется линией n-го порядка (n=1, 2, 3, …), если она определяется уравнением n- ой степени относительно текущих прямоугольных координат.
Ax+By+C=0 - кривые первого порядка;
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0 - кривые второго порядка
.Кривая первого порядка - есть прямая линия.
Уравнение с угловым коэффициентом. 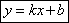
k= tg α – угловой коэффициент.Если b=0 то прямая проходит через начало координат. Уравнение примет вид
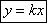
Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.
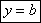
Если α=π/2, то уравнение теряет смысл. В этом случае уравнение приметвид
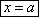
и пройдетпараллельно оси оу. Общее уравнение прямой.
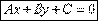
A, B, C – произвольные числа, причем А и В не равны нулю одновременно.· Если В=0, то уравнение имеет вид

или
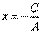
. Это уравнениепрямой, параллельной оси оу. и проходящей через точку
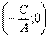
· Если В≠0, то получаем уравнение с угловым коэффициентом
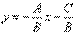
.· Если А=0, то уравнение имеет вид
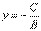
. Это уравнение прямой, параллельной оси ох.· Если С=0, то уравнение проходит через т. О (0;0). Уравнение прямой, проходящей через точку, в данном направлении.т М (х
0;у
0).Уравнение прямой записывается в виде
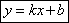
.Подставим в это уравнение точку М
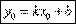
Решим систему:
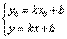
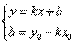
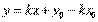
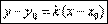
Уравнение прямой, проходящей через 2 точки.К (х
1;у
1) М (х
2;у
2)
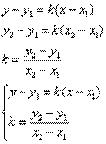
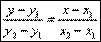
Уравнение прямой в отрезках.К (а;0); М (0;b)Подставим точки в уравнение прямой:
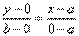
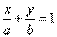
Уравнение прямой, проходящей через данную точку, перпендикулярно данному
вектору. М
0 (х
0;у
0).
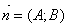
Возьмем произвольную точку М (х;у).
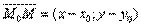
Т.к.
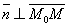
, то
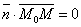
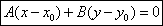
Нормальное уравнение прямой.Уравнение прямой можно записать в виде:
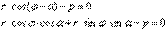
Т.к.
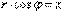
;
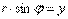
, то:
 Угол между прямыми.
Угол между прямыми. Дано: прямые L
1 и L
2 с угловыми коэффициентами
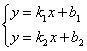
Требуется найти угол между прямыми:
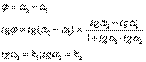
 15.Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями.
15.Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями. Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному
вектору. Пусть плоскость задана точкой M
0(x
0;y
0;z
0) и вектором
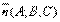
,перпендикулярной этой плоскости.Возьмем произвольную точку M(x;y;z) и составим вектор
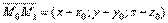
. При любом расположении точки М на плоскости Q
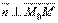
, поэтому
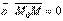
.
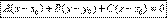
Общее уравнение плоскости.
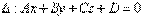
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)· Если С=0 то вектор
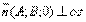
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – тоox.· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz.Аналогично при A=D=0 и B=D=0.· Если А=В=0 то уравнение примет вид
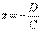
плоскость параллельна плоскости Oxy.· Если A=B=D=0, то уравнение имеет вид
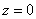
. Это уравнение плоскости Oxy. Уравнение плоскости, проходящей через три точкиК (х
1;у
1) М (х
2;у
2) N (x
3;y
3)Возьмем на плоскости точку P (x;y;z).Составим векторы:
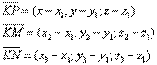
Эти векторы лежат в одной плоскости, следовательно они компланарны:

Уравнение плоскости в отрезках.Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
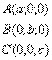
;
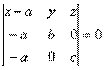
;
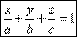
Нормальное уравнение плоскости.
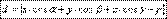 Угол между прямой и плоскостью. Расстояние от точки до плоскости.
Угол между прямой и плоскостью. Расстояние от точки до плоскости. 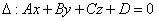
Прямая L:
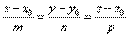
Пусть φ – угол между плоскостью и прямой.Тогда θ – угол между
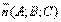
и
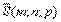
.
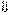
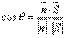
Найдем
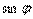
, если
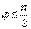
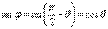
, т.к.
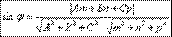
Расстояние от точки до плоскости.Дано:M
0 (x
0;y
0;z
0)
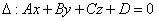
Расстояние d от точки М
0 до плоскости ∆ равно модулю проекциивектора
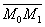
(где М
1(x1;y1;z1) - произвольная точкаплоскости) на направление нормального вектора
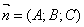

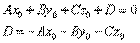
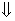

!!!Если плоскость задана уравнением:
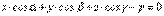
то расстояние до плоскости находится по формуле:
 16.Прямая в пространстве. Виды уравнений прямой. Угол между прямыми.
16.Прямая в пространстве. Виды уравнений прямой. Угол между прямыми. Векторное уравнение прямой.Положение прямой можно задать по точке и направляющему вектору.Пусть прямая L задана ее точкой M
0(x
0;y
0;z
0) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z).Обозначим радиус-векторы точек M и M
0 через r и r
0.
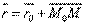
Тогда уравнение прямой запишется в виде:
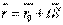
где t – скалярный множитель (параметр). Параметрические уравнения прямой.
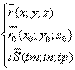
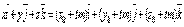
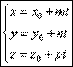
Канонические уравнения прямой.S(m;n;p) – направляющий вектор прямой L. M
0(x
0;y
0;z
0) – точка на прямой.
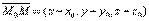
соединяет M
0 с произвольной точкой М.
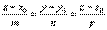
Уравнение прямой в пространстве, проходящей через две точки.M
1(x
1;y
1;z
1) M
2(x
2;y
2;z
2)В качестве направляющего вектора можно задать вектор
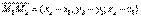
Следовательно:
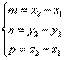
, тогда
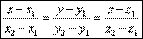
Общее уравнение прямой.Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:
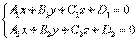
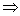
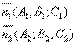
Т.к. прямая перпендикулярна векторам n
1 и n
2 тонаправляющий вектор запишется как векторное произведение:
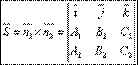 Угол между прямыми.
Угол между прямыми. 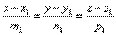
;
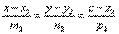
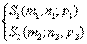
 18. Кривые второго порядка. Определения, канонические уравнения и свойства.
18. Кривые второго порядка. Определения, канонические уравнения и свойства. Кривой второго порядка на плоскости называется множество точек, удовлетворяющих уравнению
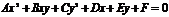 (1)
(1)
 В этом уравнении
В этом уравнении 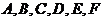 – заданные числа – параметры уравнения, для которых выполняется условие
– заданные числа – параметры уравнения, для которых выполняется условие 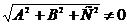 ,
, 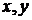 - координаты точки на плоскости.
- координаты точки на плоскости.
Уравнение (1) называют общим уравнением кривой второго порядка.
Различают три типа кривых второго порядка: эллиптический; гиперболический; параболический.
Как правило, кривые эллиптического типа – это окружности и эллипсы, кривые гиперболического типа – это гиперболы, а параболического типа – параболы.
Кроме этого, множество точек, удовлетворяющих уравнению (1), может оказаться пустым, состоять всего из одной точки, представлять собой две пересекающиеся прямые или даже одну прямую линию. Такие случаи называются вырожденными.
Примеры.
1. 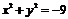 . Множество точек, удовлетворяющих этому уравнению пустое.
. Множество точек, удовлетворяющих этому уравнению пустое.
2. 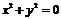 . Множество точек состоит из одной точки
. Множество точек состоит из одной точки 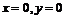 .
.
3. 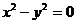 . Множество точек, удовлетворяющих этому уравнению, представляет собой две пересекающиеся прямые линии:
. Множество точек, удовлетворяющих этому уравнению, представляет собой две пересекающиеся прямые линии: 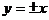 .
.
Остановимся более подробно на изучении свойств окружностей, эллипсов, гипербол и парабол.
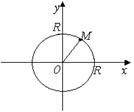
Уравнение окружности
Окружность – это множество точек, которые находятся на одинаковом расстоянии от одной заданной точки, называемой центром окружности.
 Введём систему координат так, чтобы начало координат совпадало с центром окружности. Выберем на окружности произвольную точку
Введём систему координат так, чтобы начало координат совпадало с центром окружности. Выберем на окружности произвольную точку  с координатами
с координатами  . Из определения окружности
. Из определения окружности  , где
, где 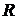 - расстояние от точек на окружности до центра. В координатной форме это условие примет вид:
- расстояние от точек на окружности до центра. В координатной форме это условие примет вид:
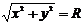 .
.
Возведя обе части уравнения в квадрат, получим каноническое уравнение окружности: 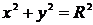 (2)
(2)
Если центр окружности расположить в точке с координатами 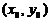 , то уравнение окружности примет вид:
, то уравнение окружности примет вид: 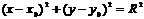 (3)
(3)
Уравнение (3) является нормальным уравнением окружности. После раскрытия скобок в этом уравнении получается общее уравнение окружности:
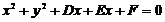 , (4)
, (4)
где 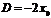 ,
, 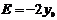 ,
,
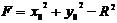 .
.
Пример 1. Найти координаты центра и радиус окружности, задаваемой уравнением: 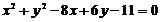 . Построить эту окружность.
. Построить эту окружность.
Решение. Сгруппируем члены, содержащие 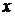 и
и 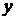 , и дополним каждую группу до полного квадрата суммы или разности:
, и дополним каждую группу до полного квадрата суммы или разности: 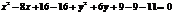 , или
, или 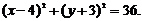
Ответ: координаты центра 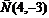 , радиус
, радиус 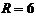 .
.
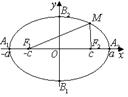
Уравнение эллипса
Эллипс – это множество точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, есть постоянная величина. Обозначим её 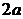 . Обозначим фокусы буквами
. Обозначим фокусы буквами 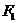 и
и 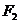 , расстояние между фокусами
, расстояние между фокусами 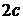 (
(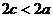 ), вершины эллипса буквами
), вершины эллипса буквами 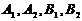 . Отрезки
. Отрезки 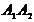 и
и 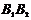 называют большой и малой осями эллипса соответственно.
называют большой и малой осями эллипса соответственно.
Введем систему координат, совместив начало координат с точкой пересечения осей 0, ось 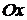 направим вдоль большой полуоси
направим вдоль большой полуоси 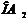 , а ось
, а ось 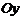 вдоль малой полуоси
вдоль малой полуоси 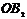 .
.
В такой системе координат уравнение эллипса примет вид:
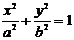 , где
, где 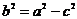 ,
, 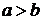 . (5)
. (5)
Уравнение (5) называют каноническим уравнением эллипса. В этом уравнении 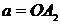 ;
; 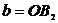 ;
; 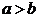 ; фокусы эллипса имеют координаты
; фокусы эллипса имеют координаты 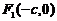 и
и 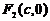 ,где
,где 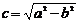 . Отношение
. Отношение 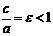 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.
 Если параллельным сдвигом центр эллипса разместить в точке с координатами
Если параллельным сдвигом центр эллипса разместить в точке с координатами 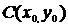 , то уравнение эллипса примет вид:
, то уравнение эллипса примет вид:
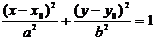 . (6)
. (6)
Пример 2. Найти координаты центра эллипса, величину большой и малой полуоси,
координаты фокусов, если эллипс задан уравнением
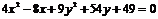 .
.
Решение. Сгруппируем члены, содержащие 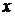 и
и 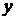 , и дополним каждую группу до полного квадрата суммы или разности:
, и дополним каждую группу до полного квадрата суммы или разности:
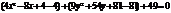 .Перегруппируем выражения в скобках, выделив полный квадрат:
.Перегруппируем выражения в скобках, выделив полный квадрат: 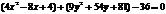 ;
; 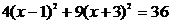 . Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса:
. Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса: 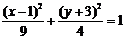 .
.
Ответ: координаты центра эллипса (1; -3), величина большой полуоси 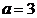 , малой полуоси
, малой полуоси
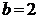 . Координаты фокусов:
. Координаты фокусов: 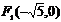 и
и 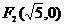 .
.
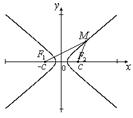
Уравнение гиперболы
Гипербола – это множество точек, разность расстояний от которых до двух данных точек (фокусов) есть постоянная величина.
Обозначим эту величину 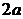 , а фокусы
, а фокусы 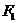 и
и 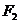 .
.
Пусть 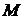 - точка на гиперболе, тогда из определения следует, что
- точка на гиперболе, тогда из определения следует, что 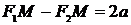 . О бозначим расстояние между фокусами
. О бозначим расстояние между фокусами 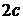 , причём
, причём 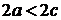 .
.
Каноническое уравнение гиперболы, симметричной относительно осей координат, примет вид
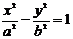 , где
, где 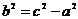 . (7)
. (7)
Обозначим вершины гиперболы буквами 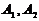 . Координаты фокусов и вершин имеют вид:
. Координаты фокусов и вершин имеют вид: 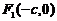 ;
; 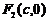 ;
; 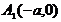 ;
; 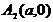 .
.
Параметр 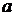 называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы, параметр
называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы, параметр 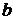 называют мнимой полуосью гиперболы, отношение
называют мнимой полуосью гиперболы, отношение 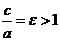 называется эксцентриситетом гиперболы. Прямые, заданные уравнениями,
называется эксцентриситетом гиперболы. Прямые, заданные уравнениями, 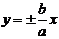 , называются асимптотами гиперболы.
, называются асимптотами гиперболы.
Если параллельным сдвигом центр гиперболы разместить в точке с координатами 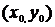 , то уравнение гиперболы примет вид:
, то уравнение гиперболы примет вид:
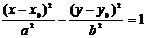 . (8)
. (8)
Пример 3. Найти координаты центра симметрии гиперболы, величину действительной и мнимой полуоси, координаты фокусов, уравнения асимптот, если гипербола задана уравнением
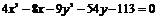 .
.
Решение. Аналогично предыдущим примерам, сгруппируем члены, содержащие 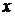 и
и 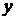 , и дополним каждую группу до полного квадрата суммы или разности:
, и дополним каждую группу до полного квадрата суммы или разности:
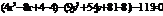 . Перегруппируем выражения в скобках, выделив полный квадрат:
. Перегруппируем выражения в скобках, выделив полный квадрат: 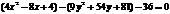 ;
; 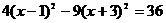 . Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса:
. Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса: 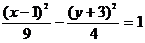 . Ответ: координаты центра гиперболы (1; -3); величина действительной полуоси
. Ответ: координаты центра гиперболы (1; -3); величина действительной полуоси 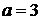 , мнимой полуоси
, мнимой полуоси 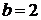 ; координаты фокусов:
; координаты фокусов: 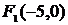 и
и 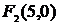 ; уравнения асимптот:
; уравнения асимптот: 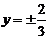
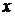 .
.
В школьном курсе математики изучаются функции 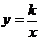 , графиками которых являются гиперболы. Асимптотами этих гипербол являются оси
, графиками которых являются гиперболы. Асимптотами этих гипербол являются оси  и
и  . Если
. Если 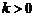 , то ветви гиперболы лежат в первой и третьей четверти декартовой системы координат. Можно показать, что фокусы и вершины этих гипербол имеют координаты вида:
, то ветви гиперболы лежат в первой и третьей четверти декартовой системы координат. Можно показать, что фокусы и вершины этих гипербол имеют координаты вида:
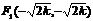 ;
; 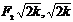 ;
; 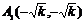 ;
; 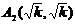 .
.
Если параллельным сдвигом центр гиперболы разместить в точке с координатами 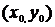 , то уравнение гиперболы примет вид
, то уравнение гиперболы примет вид 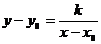 .
.
Пример 4. Доказать, что графиком дробно-линейной функции 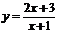 является гипербола, найти координаты центра симметрии, фокусов и вершин этой гиперболы.
является гипербола, найти координаты центра симметрии, фокусов и вершин этой гиперболы.
Решение. Выполним следующие преобразования:
\ 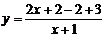 ;
; 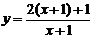 ;
; 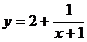 ;
; 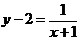 .
.
Мы получили уравнение гиперболы, центр симметрии которой имеет координаты (-1; 2), параметр 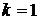 . Фокусы и вершины задаются координатами:
. Фокусы и вершины задаются координатами: 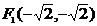 ;
; 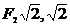 ;
; 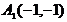 ;
; 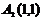 .
.
Заметим, что графиком любой дробно-линейной функции является гипербола.
Уравнение параболы
Парабола – это множество точек, одинаково удалённых от данной точки (фокуса) и от данной прямой (директрисы).
Обозначим расстояние от вершины параболы до фокуса буквой 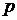 , фокус
, фокус 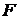 .
.
Из определения следует, что 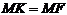 .
.
Каноническое уравнение параболы, вершина которой совпадает с началом координат, а ось симметрии с осью 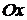 , имеет вид:
, имеет вид: 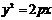 (9)
(9)
Уравнение директрисы 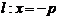 . Вершина данной параболы находится в начале координат. Фокус имеет координаты
. Вершина данной параболы находится в начале координат. Фокус имеет координаты 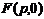 .Уравнение вида
.Уравнение вида
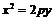 (10) описывает параболу, симметричную относительно оси
(10) описывает параболу, симметричную относительно оси 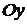 . В этом случае фокус параболы имеет координаты
. В этом случае фокус параболы имеет координаты 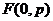 . Если параллельным сдвигом центр параболы разместить в точке с координатами
. Если параллельным сдвигом центр параболы разместить в точке с координатами 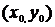 , то уравнение параболы будет иметь вид:
, то уравнение параболы будет иметь вид:
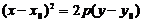 (11)
(11)
Замечание. Парабола, ось которой параллельна оси 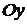 , описывается уравнением
, описывается уравнением 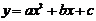 .
.
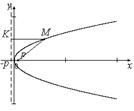 Пример 5. Уравнение параболы имеет вид:
Пример 5. Уравнение параболы имеет вид: 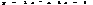 . Найти координаты вершины этой параболы, координаты фокуса и уравнение директрисы.
. Найти координаты вершины этой параболы, координаты фокуса и уравнение директрисы.
Решение. Преобразуем правую часть уравнения: 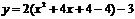 ;
; 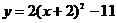 ;
; 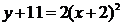 ;
; 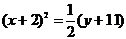 .
.
Сравнив полученное уравнение с уравнением (10), убеждаемся, что координаты вершины параболы (-2; -11); параметр 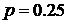 ; с учётом сдвига, координаты фокуса
; с учётом сдвига, координаты фокуса 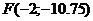 , а уравнение директрисы
, а уравнение директрисы 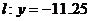 .
.
Ответ: координаты вершины параболы (-2; -11); координаты фокуса 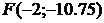 ; уравнение директрисы
; уравнение директрисы 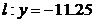 .
.
20.Линейное пространство. Определение и свойства
Определение линейного пространства
Пусть M —множество элементов произвольной природы, для которых определены операции сложения и умножения на действительное число:
· паре элементов множества 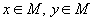 отвечает элемент
отвечает элемент 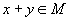 , называемый суммой x и y;
, называемый суммой x и y;
· паре 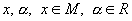 ,
, 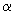 — любое действительное число, отвечает элемент
— любое действительное число, отвечает элемент 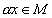 , называемый произведением числа
, называемый произведением числа 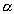 и элемента x.
и элемента x.
Будем называть множество M линейным пространством, если для всех его элементов определены операции сложения и умножения на действительное число и для любых элементов 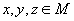 и произвольных чисел
и произвольных чисел 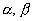 справедливо:
справедливо:
1. 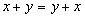 , сложение коммутативно;
, сложение коммутативно;
2. 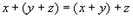 ,сложение ассоциативно;
,сложение ассоциативно;
3. существует единственный нулевой элемент 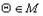 такой, что
такой, что 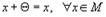 ;
;
4. для каждого элемента существует единственный противоположный элемент - x такой, что 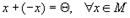 ,
,
5. 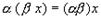 , умножение на число ассоциативно;
, умножение на число ассоциативно;
6. 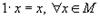 ;
;
7. 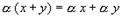 , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов;
8. 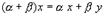 , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
Равенства 1—8 называют аксиомами линейного пространства.
Линейное пространство часто называют векторным пространством, а его элементы — векторами. Такое название, как будет показано в последующих лекциях, не случайно.
. Примеры линейных пространств
Пример 1. Нетрудно показать, что рассмотренное в п. пространство арифметических векторов R n является линейным пространством.
Пример 2. Рассмотрим множество M арифметических векторов из R n, компоненты которых — целые числа.
Это множество не является линейным пространством.
Действительно, рассмотрим вектор x = (1, 1, …, 1) и действительное число a= 0.5. Компоненты вектора x — целые числа, он принадлежит множеству M, но компоненты произведения
a x = (0.5, 0.5, …, 0.5) не являются целыми числами, и, следовательно, a x не принадлежит множеству M.
Пример 3. Рассмотрим множество M n многочленов с действительными коэффициентами относительно одного переменного, n-й степени, n >1, с определенными для многочленов операциями сложения и умножения на число.
M n = {Pn| Pn (t) = antn + an-1t n-1 + … + a1t + a0, an не равно 0}
Это множество не является линейным пространством.
Действительно., рассмотрим Pn = t n + t и Qn = - t n. Оба эти многочлена принадлежат множеству. Однако их сумма,
Pn + Qn = (t n + t)+ (- t n) = - t,
Не принадлежит M n, поскольку - t — многочлен первой степени, а множество M n содержит многочлены n -й степени,
n >1.
Пример 4. Рассмотрим множество M n многочленов с действительными коэффициентами относительно одного переменного, степени не выше n, n >1, с определенными для многочленов операциями сложения и умножения на число:
M n = {Pn| Pn (t) = antn + an-1t n-1 + … + a1t + a0},
В отличие от предыдущего примера не требуется, чтобы старший коэффициент был отличен от нуля.
Pn + Qn = Pn (t) + Qn (t) =
= (antn + an -1 t n -1 + … + a 1 t + a 0) + (bntn + bn -1 t n -1 + … + b 1 t + b 0)=
= (an + bn) tn + (an-1 + bn-1) t n -1 + … + (a 1+ b 1) t +(a 0+ b 0),
?Pn =?Pn (t) =? (antn + an-1t n-1 + … + a1t + a0) =?antn +?an-1t n-1 + … +?a1t +?a0.
Это множество является линейным пространством.
Действительно.
Во-первых, при сложении многочленов и умножении многочлена на число получается многочлен, степень которого не выше n. Т.е. каждой паре многочленов из M n соответствует их сумма — многочлен из M n. Точно так же, произведением произвольного многочлена на действительное число является многочлен той же степени, т.е. каждому многочлену из M n и каждому действительному числу? соответствует их призведение — многочлен из M n.
Во-вторых. Операции сложения многочленов и умножения многочлена на число — это операции с коэффициентами многочлена, которые являются действительными числами. А для сложения и умножения действительных чисел имеют место равенства 1-8. Нулевым элементом в M n является многочлен нулевой степени с нулевыми коэффициентами
q =q(t) =0· tn + 0· t n -1 + … + 0· t + 0 = 0
И для каждого многочлена
Pn = Pn (t) = antn + an-1t n-1 + … + a1t + a0
Определен противоположный многочлен:
-Pn = -Pn (t) = -antn - an-1t n-1 - … - a1t - a0



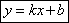 k= tg α – угловой коэффициент.Если b=0 то прямая проходит через начало координат. Уравнение примет вид
k= tg α – угловой коэффициент.Если b=0 то прямая проходит через начало координат. Уравнение примет вид 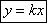 Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.
Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох. 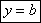 Если α=π/2, то уравнение теряет смысл. В этом случае уравнение приметвид
Если α=π/2, то уравнение теряет смысл. В этом случае уравнение приметвид 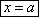 и пройдетпараллельно оси оу. Общее уравнение прямой.
и пройдетпараллельно оси оу. Общее уравнение прямой. 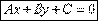 A, B, C – произвольные числа, причем А и В не равны нулю одновременно.· Если В=0, то уравнение имеет вид
A, B, C – произвольные числа, причем А и В не равны нулю одновременно.· Если В=0, то уравнение имеет вид  или
или 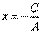 . Это уравнениепрямой, параллельной оси оу. и проходящей через точку
. Это уравнениепрямой, параллельной оси оу. и проходящей через точку 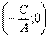 · Если В≠0, то получаем уравнение с угловым коэффициентом
· Если В≠0, то получаем уравнение с угловым коэффициентом 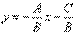 .· Если А=0, то уравнение имеет вид
.· Если А=0, то уравнение имеет вид 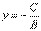 . Это уравнение прямой, параллельной оси ох.· Если С=0, то уравнение проходит через т. О (0;0). Уравнение прямой, проходящей через точку, в данном направлении.т М (х0;у0).Уравнение прямой записывается в виде
. Это уравнение прямой, параллельной оси ох.· Если С=0, то уравнение проходит через т. О (0;0). Уравнение прямой, проходящей через точку, в данном направлении.т М (х0;у0).Уравнение прямой записывается в виде 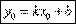 Решим систему:
Решим систему: 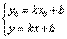
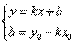
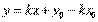
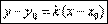 Уравнение прямой, проходящей через 2 точки.К (х1;у1) М (х2;у2)
Уравнение прямой, проходящей через 2 точки.К (х1;у1) М (х2;у2) 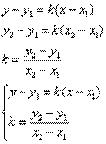
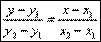 Уравнение прямой в отрезках.К (а;0); М (0;b)Подставим точки в уравнение прямой:
Уравнение прямой в отрезках.К (а;0); М (0;b)Подставим точки в уравнение прямой: 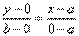
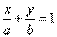 Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору. М0 (х0;у0).
Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору. М0 (х0;у0). 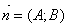 Возьмем произвольную точку М (х;у).
Возьмем произвольную точку М (х;у). 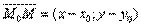 Т.к.
Т.к. 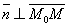 , то
, то 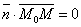
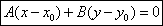 Нормальное уравнение прямой.Уравнение прямой можно записать в виде:
Нормальное уравнение прямой.Уравнение прямой можно записать в виде: 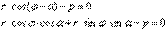 Т.к.
Т.к. 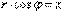 ;
; 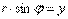 , то:
, то:  Угол между прямыми. Дано: прямые L1 и L2 с угловыми коэффициентами
Угол между прямыми. Дано: прямые L1 и L2 с угловыми коэффициентами 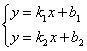 Требуется найти угол между прямыми:
Требуется найти угол между прямыми: 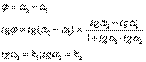
 15.Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями. Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному вектору. Пусть плоскость задана точкой M0(x0;y0;z0) и вектором
15.Плоскость в пространстве. Виды уравнения плоскостей. Угол между плоскостями. Уравнение плоскости, проходящей через заданную точку, перпендикулярно данному вектору. Пусть плоскость задана точкой M0(x0;y0;z0) и вектором 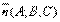 ,перпендикулярной этой плоскости.Возьмем произвольную точку M(x;y;z) и составим вектор
,перпендикулярной этой плоскости.Возьмем произвольную точку M(x;y;z) и составим вектор 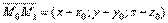 . При любом расположении точки М на плоскости Q
. При любом расположении точки М на плоскости Q 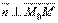 , поэтому
, поэтому 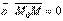 .
. 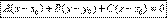 Общее уравнение плоскости.
Общее уравнение плоскости. 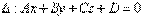 · Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)· Если С=0 то вектор
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)· Если С=0 то вектор 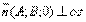 . Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – тоox.· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz.Аналогично при A=D=0 и B=D=0.· Если А=В=0 то уравнение примет вид
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – тоox.· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz.Аналогично при A=D=0 и B=D=0.· Если А=В=0 то уравнение примет вид 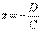 плоскость параллельна плоскости Oxy.· Если A=B=D=0, то уравнение имеет вид
плоскость параллельна плоскости Oxy.· Если A=B=D=0, то уравнение имеет вид 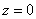 . Это уравнение плоскости Oxy. Уравнение плоскости, проходящей через три точкиК (х1;у1) М (х2;у2) N (x3;y3)Возьмем на плоскости точку P (x;y;z).Составим векторы:
. Это уравнение плоскости Oxy. Уравнение плоскости, проходящей через три точкиК (х1;у1) М (х2;у2) N (x3;y3)Возьмем на плоскости точку P (x;y;z).Составим векторы: 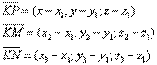 Эти векторы лежат в одной плоскости, следовательно они компланарны:
Эти векторы лежат в одной плоскости, следовательно они компланарны:  Уравнение плоскости в отрезках.Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
Уравнение плоскости в отрезках.Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки: 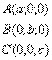 ;
; 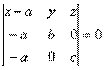 ;
; 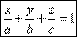 Нормальное уравнение плоскости.
Нормальное уравнение плоскости. 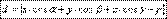 Угол между прямой и плоскостью. Расстояние от точки до плоскости.
Угол между прямой и плоскостью. Расстояние от точки до плоскости. 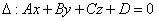 Прямая L:
Прямая L: 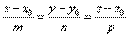 Пусть φ – угол между плоскостью и прямой.Тогда θ – угол между
Пусть φ – угол между плоскостью и прямой.Тогда θ – угол между 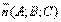 и
и 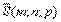 .
. 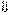
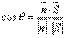 Найдем
Найдем 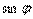 , если
, если 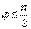
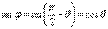 , т.к.
, т.к. 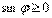
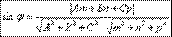 Расстояние от точки до плоскости.Дано:M0 (x0;y0;z0)
Расстояние от точки до плоскости.Дано:M0 (x0;y0;z0) 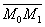 (где М1(x1;y1;z1) - произвольная точкаплоскости) на направление нормального вектора
(где М1(x1;y1;z1) - произвольная точкаплоскости) на направление нормального вектора 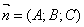

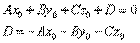
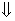
 !!!Если плоскость задана уравнением:
!!!Если плоскость задана уравнением: 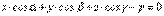 то расстояние до плоскости находится по формуле:
то расстояние до плоскости находится по формуле:  16.Прямая в пространстве. Виды уравнений прямой. Угол между прямыми. Векторное уравнение прямой.Положение прямой можно задать по точке и направляющему вектору.Пусть прямая L задана ее точкой M0(x0;y0;z0) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z).Обозначим радиус-векторы точек M и M0 через r и r0.
16.Прямая в пространстве. Виды уравнений прямой. Угол между прямыми. Векторное уравнение прямой.Положение прямой можно задать по точке и направляющему вектору.Пусть прямая L задана ее точкой M0(x0;y0;z0) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z).Обозначим радиус-векторы точек M и M0 через r и r0. 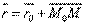 Тогда уравнение прямой запишется в виде:
Тогда уравнение прямой запишется в виде: 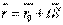 где t – скалярный множитель (параметр). Параметрические уравнения прямой.
где t – скалярный множитель (параметр). Параметрические уравнения прямой. 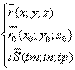
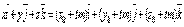
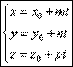 Канонические уравнения прямой.S(m;n;p) – направляющий вектор прямой L. M0(x0;y0;z0) – точка на прямой.
Канонические уравнения прямой.S(m;n;p) – направляющий вектор прямой L. M0(x0;y0;z0) – точка на прямой. 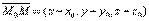 соединяет M0 с произвольной точкой М.
соединяет M0 с произвольной точкой М. 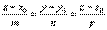 Уравнение прямой в пространстве, проходящей через две точки.M1(x1;y1;z1) M2(x2;y2;z2)В качестве направляющего вектора можно задать вектор
Уравнение прямой в пространстве, проходящей через две точки.M1(x1;y1;z1) M2(x2;y2;z2)В качестве направляющего вектора можно задать вектор 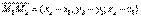 Следовательно:
Следовательно: 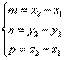 , тогда
, тогда  Общее уравнение прямой.Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:
Общее уравнение прямой.Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим: 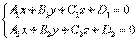
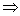
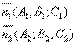 Т.к. прямая перпендикулярна векторам n1 и n2 тонаправляющий вектор запишется как векторное произведение:
Т.к. прямая перпендикулярна векторам n1 и n2 тонаправляющий вектор запишется как векторное произведение:  Угол между прямыми.
Угол между прямыми. 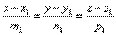 ;
; 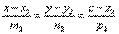
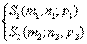
 18. Кривые второго порядка. Определения, канонические уравнения и свойства.
18. Кривые второго порядка. Определения, канонические уравнения и свойства. 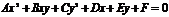 (1)
(1) В этом уравнении
В этом уравнении 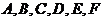 – заданные числа – параметры уравнения, для которых выполняется условие
– заданные числа – параметры уравнения, для которых выполняется условие 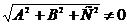 ,
, 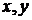 - координаты точки на плоскости.
- координаты точки на плоскости.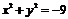 . Множество точек, удовлетворяющих этому уравнению пустое.
. Множество точек, удовлетворяющих этому уравнению пустое.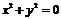 . Множество точек состоит из одной точки
. Множество точек состоит из одной точки 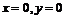 .
.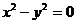 . Множество точек, удовлетворяющих этому уравнению, представляет собой две пересекающиеся прямые линии:
. Множество точек, удовлетворяющих этому уравнению, представляет собой две пересекающиеся прямые линии: 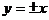 .
. Введём систему координат так, чтобы начало координат совпадало с центром окружности. Выберем на окружности произвольную точку
Введём систему координат так, чтобы начало координат совпадало с центром окружности. Выберем на окружности произвольную точку  с координатами
с координатами 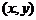 . Из определения окружности
. Из определения окружности  , где
, где 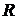 - расстояние от точек на окружности до центра. В координатной форме это условие примет вид:
- расстояние от точек на окружности до центра. В координатной форме это условие примет вид: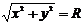 .
.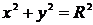 (2)
(2)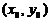 , то уравнение окружности примет вид:
, то уравнение окружности примет вид: 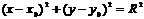 (3)
(3)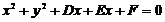 , (4)
, (4)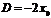 ,
, 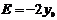 ,
,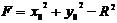 .
.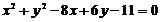 . Построить эту окружность.
. Построить эту окружность. и
и  , и дополним каждую группу до полного квадрата суммы или разности:
, и дополним каждую группу до полного квадрата суммы или разности: 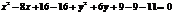 , или
, или 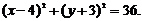
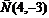 , радиус
, радиус 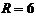 .
.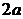 . Обозначим фокусы буквами
. Обозначим фокусы буквами 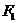 и
и 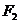 , расстояние между фокусами
, расстояние между фокусами 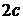 (
(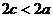 ), вершины эллипса буквами
), вершины эллипса буквами 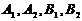 . Отрезки
. Отрезки 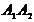 и
и 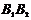 называют большой и малой осями эллипса соответственно.
называют большой и малой осями эллипса соответственно.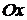 направим вдоль большой полуоси
направим вдоль большой полуоси 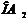 , а ось
, а ось 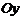 вдоль малой полуоси
вдоль малой полуоси 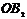 .
.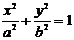 , где
, где 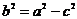 ,
, 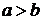 . (5)
. (5)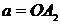 ;
; 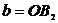 ;
; 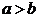 ; фокусы эллипса имеют координаты
; фокусы эллипса имеют координаты 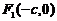 и
и 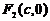 ,где
,где 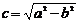 . Отношение
. Отношение 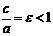 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса. Если параллельным сдвигом центр эллипса разместить в точке с координатами
Если параллельным сдвигом центр эллипса разместить в точке с координатами 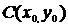 , то уравнение эллипса примет вид:
, то уравнение эллипса примет вид: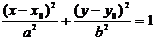 . (6)
. (6)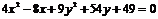 .
.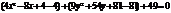 .Перегруппируем выражения в скобках, выделив полный квадрат:
.Перегруппируем выражения в скобках, выделив полный квадрат: 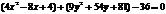 ;
; 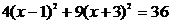 . Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса:
. Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса: 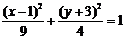 .
.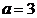 , малой полуоси
, малой полуоси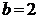 . Координаты фокусов:
. Координаты фокусов: 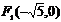 и
и 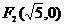 .
.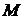 - точка на гиперболе, тогда из определения следует, что
- точка на гиперболе, тогда из определения следует, что 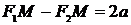 . О бозначим расстояние между фокусами
. О бозначим расстояние между фокусами 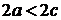 .
.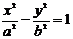 , где
, где 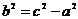 . (7)
. (7)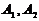 . Координаты фокусов и вершин имеют вид:
. Координаты фокусов и вершин имеют вид: 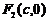 ;
; 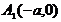 ;
; 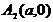 .
.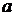 называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы, параметр
называют вещественной полуосью гиперболы, и представляет собой расстояние от начала координат до вершины гиперболы, параметр 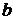 называют мнимой полуосью гиперболы, отношение
называют мнимой полуосью гиперболы, отношение 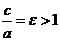 называется эксцентриситетом гиперболы. Прямые, заданные уравнениями,
называется эксцентриситетом гиперболы. Прямые, заданные уравнениями, 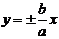 , называются асимптотами гиперболы.
, называются асимптотами гиперболы.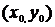 , то уравнение гиперболы примет вид:
, то уравнение гиперболы примет вид: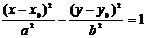 . (8)
. (8)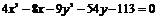 .
.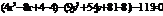 . Перегруппируем выражения в скобках, выделив полный квадрат:
. Перегруппируем выражения в скобках, выделив полный квадрат: 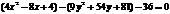 ;
; 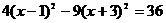 . Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса:
. Разделив левую и правую части выражения на 36, получим каноническое уравнение эллипса: 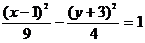 . Ответ: координаты центра гиперболы (1; -3); величина действительной полуоси
. Ответ: координаты центра гиперболы (1; -3); величина действительной полуоси 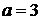 , мнимой полуоси
, мнимой полуоси 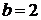 ; координаты фокусов:
; координаты фокусов: 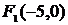 и
и 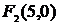 ; уравнения асимптот:
; уравнения асимптот: 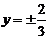
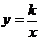 , графиками которых являются гиперболы. Асимптотами этих гипербол являются оси
, графиками которых являются гиперболы. Асимптотами этих гипербол являются оси 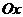 и
и 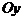 . Если
. Если 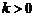 , то ветви гиперболы лежат в первой и третьей четверти декартовой системы координат. Можно показать, что фокусы и вершины этих гипербол имеют координаты вида:
, то ветви гиперболы лежат в первой и третьей четверти декартовой системы координат. Можно показать, что фокусы и вершины этих гипербол имеют координаты вида: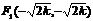 ;
; 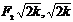 ;
; 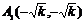 ;
; 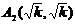 .
.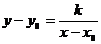 .
.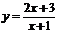 является гипербола, найти координаты центра симметрии, фокусов и вершин этой гиперболы.
является гипербола, найти координаты центра симметрии, фокусов и вершин этой гиперболы.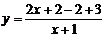 ;
; 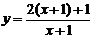 ;
; 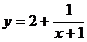 ;
; 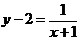 .
.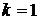 . Фокусы и вершины задаются координатами:
. Фокусы и вершины задаются координатами: 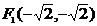 ;
; 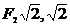 ;
; 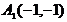 ;
; 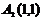 .
.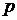 , фокус
, фокус 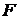 .
.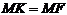 .
.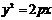 (9)
(9)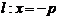 . Вершина данной параболы находится в начале координат. Фокус имеет координаты
. Вершина данной параболы находится в начале координат. Фокус имеет координаты 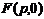 .Уравнение вида
.Уравнение вида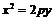 (10) описывает параболу, симметричную относительно оси
(10) описывает параболу, симметричную относительно оси 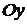 . В этом случае фокус параболы имеет координаты
. В этом случае фокус параболы имеет координаты 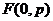 . Если параллельным сдвигом центр параболы разместить в точке с координатами
. Если параллельным сдвигом центр параболы разместить в точке с координатами 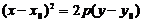 (11)
(11)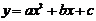 .
. Пример 5. Уравнение параболы имеет вид:
Пример 5. Уравнение параболы имеет вид: 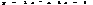 . Найти координаты вершины этой параболы, координаты фокуса и уравнение директрисы.
. Найти координаты вершины этой параболы, координаты фокуса и уравнение директрисы.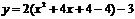 ;
; 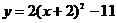 ;
; 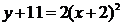 ;
; 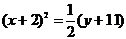 .
.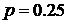 ; с учётом сдвига, координаты фокуса
; с учётом сдвига, координаты фокуса 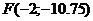 , а уравнение директрисы
, а уравнение директрисы 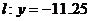 .
.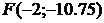 ; уравнение директрисы
; уравнение директрисы 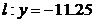 .
.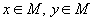 отвечает элемент
отвечает элемент 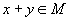 , называемый суммой x и y;
, называемый суммой x и y;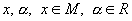 ,
, 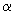 — любое действительное число, отвечает элемент
— любое действительное число, отвечает элемент 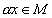 , называемый произведением числа
, называемый произведением числа 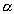 и элемента x.
и элемента x.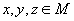 и произвольных чисел
и произвольных чисел 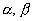 справедливо:
справедливо: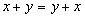 , сложение коммутативно;
, сложение коммутативно;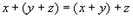 ,сложение ассоциативно;
,сложение ассоциативно;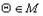 такой, что
такой, что 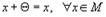 ;
;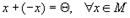 ,
,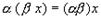 , умножение на число ассоциативно;
, умножение на число ассоциативно;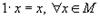 ;
;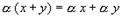 , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов;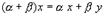 , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.