Геометрическим вектором называют направленный отрезок. Для описания векторов используют обозначения 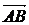 ;
;  .
.

Длиной вектора называют расстояние между начальной точкой и точкой конца вектора. Длину вектора будем обозначать  ,
, 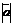 или просто АВ, а.
или просто АВ, а.
Вектор называют нулевым, если его начало и конец совпадают. Такой вектор не имеет направления, его длина равна нулю, обозначают его как  .
.
Векторы называют коллинеарными, если они лежат на одной прямой или на параллельных прямых. Обозначают это как  .
.

Векторы называют компланарными, если они лежат в одной плоскости.
Два вектора называют равными, если они коллинеарны, имеют одинаковую длину и направление.
Свободным называют вектор, который можно перемещать в пространстве параллельно его направлению.
Отметим, что для свободного вектора его начало можно совмещать с любой точкой пространства.
В дальнейшем будем иметь дело лишь со свободными векторами.
Линейные операции над векторами и их свойства
Линейными операциями над векторами являются сложение векторов и умножение вектора на число.
Суммой двух геометрических векторов  и
и  называется вектор
называется вектор  , который можно построить или по правилу треугольника или по правилу параллелограмма.
, который можно построить или по правилу треугольника или по правилу параллелограмма.
1.По правилу треугольника
Параллельным переносом совместим конец вектора  с началом вектора
с началом вектора  . Тогда суммой
. Тогда суммой  +
+  будем называть вектор
будем называть вектор 
 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  , а конец с концом вектора
, а конец с концом вектора  .
.
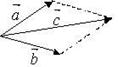
2. По правилу параллелограмма
Параллельным переносом совместим начало вектора  и начало вектора
и начало вектора  . Достроим параллелограмм на концах векторов. Суммой векторов
. Достроим параллелограмм на концах векторов. Суммой векторов  и
и  будем называть вектор
будем называть вектор  , являющийся диагональю параллелограмма, начало которого совпадает с началом векторов
, являющийся диагональю параллелограмма, начало которого совпадает с началом векторов  и
и  .
.
Свойства сложения векторов.
1. Коммутативность
 +
+  =
=  +
+ 
2.Ассоциативность 
3.Существование нулевого вектора  такого, что
такого, что
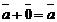
4. Для любого вектора  существует противоположный вектор (
существует противоположный вектор ( )такой, что
)такой, что

С помощью свойств сложения векторов также можно доказать, что для любых векторов  и
и  существует такой вектор
существует такой вектор  , который, будучи сложен с
, который, будучи сложен с  , даст вектор
, даст вектор  .
.

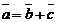
Такой вектор  называют геометрической разностью векторов
называют геометрической разностью векторов  и
и  :
: 
Произведением 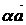 вектора
вектора  на вещественное число
на вещественное число  называется вектор
называется вектор  , имеющий длину, равную произведению чисел
, имеющий длину, равную произведению чисел  и направление, совпадающее с направлением вектора
и направление, совпадающее с направлением вектора  , если
, если  , и противоположное, если
, и противоположное, если  .
.
Свойства произведения вектора на число.
5. Ассоциативность сомножителей

6. Дистрибутивность суммы векторов относительно умножения на вещественное число

7. Дистрибутивность относительно суммы чисел 
8. Существование числа 1, не меняющего вектора при умножении

Все восемь свойств линейных операций получены из геометрических свойств векторов.
Можно поступить иначе. Положить эти восемь свойств в основу определения векторов.
Определение.
Любая совокупность объектов, для которых введено соотношение равенства, а также операции сложения и умножения на число, удовлетворяющие свойствам 1-8, называется линейным векторным пространством.
Элементы такого пространства называют векторами или точками этого пространства.
Примеры линейных векторных пространств
1. Множество всех геометрических векторов.
2. Множество всех вещественных чисел. Обозначим его  или
или 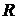 .
.
3. Множество всевозможных пар вещественных чисел. Обозначим его  .
.
Пусть 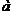 =
=  и
и  =
=  – элементы этого множества. Будем называть числа
– элементы этого множества. Будем называть числа  и
и  координатами векторов
координатами векторов  и
и  . Векторы
. Векторы  и
и  считаются равными, если равны их координаты, т.е.
считаются равными, если равны их координаты, т.е.  и
и 
Суммой векторов  и
и 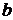 будем называть вектор
будем называть вектор  , имеющий координаты
, имеющий координаты  и
и  .
.
Произведением вектора  на число
на число  будем считать вектор
будем считать вектор  , имеющий координаты
, имеющий координаты  и
и  .
.
При таком введении линейных операций выполняются все свойства 1-8 и пространство  можно считать линейным векторным пространством.
можно считать линейным векторным пространством.
4. Множество всевозможных наборов из n вещественных чисел. Будем обозначать это множество 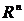 . Элементами этого множества являются наборы из
. Элементами этого множества являются наборы из  чисел.
чисел.
10. Скалярное произведение векторов и его свойства
В качестве нелинейных операций над векторами рассмотрим скалярное произведение и векторное произведение, наиболее часто встречающиеся в приложениях.
Углом между двумя векторами будем называть угол, который не превосходит p.
Угол между векторами будем обозначать 
Скалярным произведением двух геометрических векторов называется число, равное произведению длин этих векторов на косинус угла между ними: 
Если  ,то
,то  ,т.к.
,т.к.  ,
,
если  ,то
,то  ,т.к.
,т.к.  ,
,
если  ,то
,то 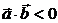 ,т.к.
,т.к.  .
.
а)Ортогональной проекцией вектора  на направление, задаваемое вектором
на направление, задаваемое вектором  , будем называть число
, будем называть число 

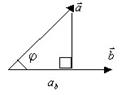
б) Аналогично число  =
=  является ортогональной проекцией вектора
является ортогональной проекцией вектора  на направление
на направление  .
.

Из определения скалярного произведения следует, что

Следствие.
Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы ортогональны (угол между ними равен  ).
).
Свойства скалярного произведения.
Коммутативность

1) Ассоциативность
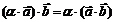
2) Дистрибутивность относительно суммы векторов

4)  , если
, если  и
и  , если
, если 
Свойства 1-4 доказываются исходя из геометрических свойств векторов.
Угол между векторами.
Зная длины векторов и их скалярное произведение можно найти угол между векторами. Действительно, т.к.  , то
, то

11. Векторное произведение и его свойства, вычисление через координаты
Векторным произведением  вектора
вектора  на вектор
на вектор  называется вектор (обозначим его
называется вектор (обозначим его  ), удовлетворяющий следующим условиям.
), удовлетворяющий следующим условиям.
1.  , где
, где 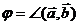 .
.
2.  и
и 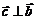 .
.
3. Направление вектора  выбрано так, что со стороны вектора
выбрано так, что со стороны вектора  поворот от
поворот от  к
к  происходит против часовой стрелки.
происходит против часовой стрелки.
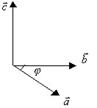
Свойства векторного произведения.
1. 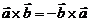
2.  ,
,  - вещественное число
- вещественное число
3. 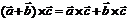
Пример
Найти площадь параллелограмма и угол  между его диагоналями, если длина сторон параллелограмма
между его диагоналями, если длина сторон параллелограмма 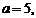
 и угол между ними
и угол между ними  .
.

Решение.
Пусть  и
и  - векторы, построенные на сторонах параллелограмма. Площадь параллелограмма
- векторы, построенные на сторонах параллелограмма. Площадь параллелограмма  .
.  Заметим, что
Заметим, что  . Диагонали параллелограмма – это векторы
. Диагонали параллелограмма – это векторы  и
и  .
.
Пусть  - угол между диагоналями. Тогда
- угол между диагоналями. Тогда
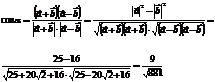
Ответ:  ;
;  .
.
Векторное произведение векторов.
Определение: Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что
- | [ a, b ] |=S a , b , где S a , b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то S a , b =0.)
- a
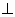 [a,b]
[a,b] 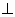 b.
b. - a, b, [a,b] – правая тройка.
Свойства векторного произведения:
- [ a, b ] = -[ b, a ]
- [ a, b ] = θ ó a || b
- [ a1 + a2, b ] = [ a1, b ]+[ a2, b ]
- λ·[ a, b ] = [λ ·a,b ] = [ a,λ ·b ]
 λ
λ  R.
R.
Утверждение 2: В декартовой системе координат (базис i, j, k), a={ x1, y1, z1 }, b={ x2, y2, z2 }
=> [ a, b ] = 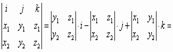
= 
12. Смешанное произведение векторов.
Определение: Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c).
Утверждение: <a,b,c>=V a , b , c, если a,b,c – правая тройка, или <a,b,c>= -V a , b , c, если a,b,c – левая тройка. Здесь V a , b , c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то Va,b,c=0.)
Утверждение: В декартовой системе координат, если a={ x1, y1, z1 }, b={ x2, y2, z2 },
с={ x3, y3, z3 }, => <a,b,c>= 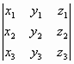 .
.



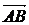 ;
;  .
.
 ,
, 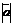 или просто АВ, а.
или просто АВ, а. .
. .
.
 и
и  называется вектор
называется вектор  , который можно построить или по правилу треугольника или по правилу параллелограмма.
, который можно построить или по правилу треугольника или по правилу параллелограмма. . Тогда суммой
. Тогда суммой 
 , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора  . Достроим параллелограмм на концах векторов. Суммой векторов
. Достроим параллелограмм на концах векторов. Суммой векторов 

 такого, что
такого, что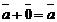
 )такой, что
)такой, что
 .
.
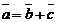

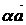 вектора
вектора  на вещественное число
на вещественное число  называется вектор
называется вектор  и направление, совпадающее с направлением вектора
и направление, совпадающее с направлением вектора  , и противоположное, если
, и противоположное, если  .
.



 или
или 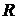 .
. .
.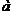 =
=  и
и  =
=  – элементы этого множества. Будем называть числа
– элементы этого множества. Будем называть числа  и
и  координатами векторов
координатами векторов  и
и  . Векторы
. Векторы  и
и  считаются равными, если равны их координаты, т.е.
считаются равными, если равны их координаты, т.е.  и
и 
 и
и 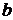 будем называть вектор
будем называть вектор  , имеющий координаты
, имеющий координаты  и
и  .
. будем считать вектор
будем считать вектор  , имеющий координаты
, имеющий координаты  и
и  .
.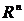 . Элементами этого множества являются наборы из
. Элементами этого множества являются наборы из  чисел.
чисел.

 ,то
,то  ,т.к.
,т.к.  ,
, ,то
,то  ,т.к.
,т.к.  ,
, ,то
,то 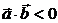 ,т.к.
,т.к.  .
. на направление, задаваемое вектором
на направление, задаваемое вектором  , будем называть число
, будем называть число 


 =
=  является ортогональной проекцией вектора
является ортогональной проекцией вектора  на направление
на направление  .
.

 ).
).
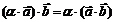

 , если
, если  и
и  , если
, если 
 , то
, то
 вектора
вектора  на вектор
на вектор  ), удовлетворяющий следующим условиям.
), удовлетворяющий следующим условиям. , где
, где 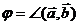 .
. и
и 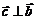 .
.
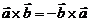
 ,
,  - вещественное число
- вещественное число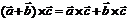
 между его диагоналями, если длина сторон параллелограмма
между его диагоналями, если длина сторон параллелограмма 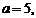
 и угол между ними
и угол между ними  .
.
 .
.  Заметим, что
Заметим, что  . Диагонали параллелограмма – это векторы
. Диагонали параллелограмма – это векторы  и
и  .
.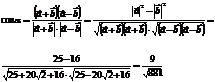
 ;
;  .
.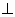 [a,b]
[a,b]  λ
λ  R.
R. 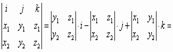

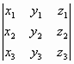 .
.


