Аналитическая геометрия на плоскости
Координаты точки на прямой и на плоскости.
Деление отрезка в данном отношении.
■ Деление отрезка в данном отношении. Пусть даны точки 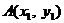 и
и  . Координаты точки
. Координаты точки  , делящей отрезок АВ в отношении
, делящей отрезок АВ в отношении 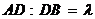 , определяются по формулам
, определяются по формулам
 ,
,  .
.
В частности, координаты середины отрезка (т.е. точки  , делящей отрезок АВ в отношении
, делящей отрезок АВ в отношении  ) находятся по формулам
) находятся по формулам
 ,
,  .
.
Пример 1. Найти точку  , делящую отрезок АВ в отношении
, делящую отрезок АВ в отношении 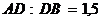 , если даны координаты точек
, если даны координаты точек 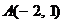 и
и  .
.
Решение. Находим
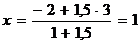 ,
,  .
.
Ответ: 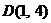 .
.
Пример 2. Найти середину  отрезка АВ из Примера 1.
отрезка АВ из Примера 1.
Решение. Находим
 ,
,  .
.
Ответ:  .
.
Примеры уравнений кривых в полярных координатах
Уравнения некоторых кривых в полярных координатах выглядят значительно проще, чем в декартовой системе координат. Приведем примеры (для простоты на всех рисунках предполагается, что параметр а положителен).
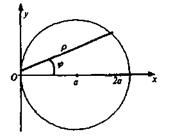 Окружность
Окружность  или или 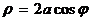 Рис. 8
Рис. 8
|  Кардиоида
Кардиоида 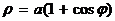 Рис. 9
Рис. 9
|
 Спираль Архимеда
Спираль Архимеда  Рис. 10
Рис. 10
| 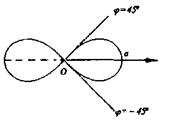 Лемниската Бернулли
Лемниската Бернулли  Рис. 11
Рис. 11
|
Прямая линия на плоскости. Различные виды уравнения прямой
■ Уравнение прямой с угловым коэффициентом. Если прямая не параллельна оси Оу, то ее уравнение можно записать в виде
 .
.
Это уравнение называется уравнением прямой с угловым коэффициентом; в нем  , а b – ордината точки пересечения прямой с осью Оу.
, а b – ордината точки пересечения прямой с осью Оу.
При  имеем
имеем  – уравнение прямой, проходящей через начало координат.
– уравнение прямой, проходящей через начало координат.
■ Общее уравнение прямой. Любая прямая на плоскости определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
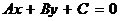
(где А и В не равны нулю одновременно) определяет некоторую прямую. Это уравнение называется общим уравнением прямой. В отличие от уравнения  оно может определять всевозможные прямые на плоскости без исключения.
оно может определять всевозможные прямые на плоскости без исключения.
Частные случаи.
а) при 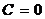 прямая проходит через начало координат;
прямая проходит через начало координат;
б) при 
 уравнение примет вид
уравнение примет вид 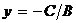 – прямая параллельна оси Ох (в частности,
– прямая параллельна оси Ох (в частности,  – уравнение самой оси Ох);
– уравнение самой оси Ох);
в) при 
 уравнение примет вид
уравнение примет вид  – прямая параллельна оси Оу (в частности,
– прямая параллельна оси Оу (в частности, 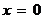 – уравнение самой оси Оу).
– уравнение самой оси Оу).
Из общего уравнения прямой при  можно получить уравнение
можно получить уравнение  , т.е. уравнение прямой с угловым коэффициентом
, т.е. уравнение прямой с угловым коэффициентом  .
.
 2) подставляем в левую часть нормального уравнения прямой координаты
2) подставляем в левую часть нормального уравнения прямой координаты  ,
, 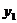 данной точки М.
данной точки М.
Тогда искомое расстояние равно абсолютной величине полученного при этом числа h.
Замечание. Если 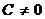 , т.е. если прямая не проходит через начало координат, то при
, т.е. если прямая не проходит через начало координат, то при  точка М и начало координат лежат по одну сторону от данной прямой, а при
точка М и начало координат лежат по одну сторону от данной прямой, а при  – по разные стороны (при
– по разные стороны (при  , очевидно, точка М лежит на прямой).
, очевидно, точка М лежит на прямой).
Пример __. Найти расстояние от точки  до прямой
до прямой  .
.
Решение. Нормальное уравнение прямой имеет вид  , поэтому
, поэтому  .
.
Ответ: искомое расстояние равно  .
.
Аналитическая геометрия на плоскости
Координаты точки на прямой и на плоскости.
Расстояние между двумя точками
■ Числовая ось. Интервалы. Числовой осью называется прямая, на которой заданы: а) некоторая точка О – начало отсчета; б) направление, которое считается положительным; в) единичный отрезок (масштаб).
Каждое действительное число изображается точкой числовой оси (число х изображается точкой А). Устанавливается взаимно однозначное соответствие между множеством действительных чисел и множеством точек числовой прямой.
Число х называется координатой точки А. Расстояние от начала отсчета до точки А равно | х |, расстояние между двумя точками  и
и  (т.е. длина отрезка АВ) равно
(т.е. длина отрезка АВ) равно 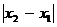 .
.
Пример 1. Для точек А (2), В (-3) имеем: длина отрезка АВ равна  , серединой отрезка АВ является точка
, серединой отрезка АВ является точка 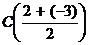 , т.е. точка
, т.е. точка  .
.
Окрестностью точки  числовой оси называется любой интервал, содержащий эту точку. В частности,
числовой оси называется любой интервал, содержащий эту точку. В частности, 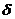 -окрестность точки
-окрестность точки  – симметричный интервал вида
– симметричный интервал вида  или множество чисел х, удовлетворяющих условию
или множество чисел х, удовлетворяющих условию 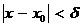 (где
(где 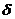 – заданное положительное число).
– заданное положительное число).
■ Декартова прямоугольная система координат на плоскости задается фиксированной точкой О (называемой началом координат) и парой пересекающихся в этой точке взаимно перпендикулярных прямых (называемых осями координат). Каждая из этих осей рассматривается как числовая ось с началом отсчета в точке О.
Имеет место взаимно однозначное соответствие между точками плоскости и парами действительных чисел  – координатами точек (см. рис. 1). Координата х называется абсциссой, а координата у – ординатой точки.
– координатами точек (см. рис. 1). Координата х называется абсциссой, а координата у – ординатой точки.
■ Расстояние d между двумя точками плоскости  и
и  (т.е. длина отрезка АВ) вычисляется по формуле
(т.е. длина отрезка АВ) вычисляется по формуле
 .
.
В частности, расстояние от точки  до начала координат равно
до начала координат равно  .
.
■ Полярные координаты. Рассмотрим произвольную (фиксированную) точку плоскости О ("полюс") и проведем из нее полупрямую, называемую полярной осью (с определенным масштабом). Зададим направление отсчета углов вокруг точки О против часовой стрелки. Тогда каждой точке М плоскости соответствуют два числа: полярный радиус  и полярный угол
и полярный угол  , где
, где  представляет собой расстояние от точки М до полюса О, а
представляет собой расстояние от точки М до полюса О, а  – угол, образуемый полярной осью с отрезком ОМ (рис. 2).
– угол, образуемый полярной осью с отрезком ОМ (рис. 2).
Эти числа  и
и  называются полярными координатами точки М. При этом полярный радиус
называются полярными координатами точки М. При этом полярный радиус  определен однозначно, а значение полярного угла
определен однозначно, а значение полярного угла  определяется с точностью до слагаемого
определяется с точностью до слагаемого  (где n – любое целое число).
(где n – любое целое число).

При этом у точки О полярный радиус  , а полярный угол
, а полярный угол  не имеет определенного значения (ему можно приписать любое значение).
не имеет определенного значения (ему можно приписать любое значение).
Чтобы соответствие между точками плоскости (отличными от полюса) и парами полярных координат 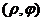 было взаимно однозначным, иногда ограничивают возможные значения полярного угла
было взаимно однозначным, иногда ограничивают возможные значения полярного угла  ; например, часто берут
; например, часто берут  или
или  .
.
Декартовы координаты точки (х, у) выражаются через полярные координаты 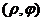 той же точки по формулам
той же точки по формулам
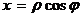 ,
, 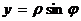
(здесь считается, что полюс совпадает с началом координат, а полярная ось совпадает с положительной полуосью абсцисс). Например, для точки М на рис. 2 значения полярных координат  ,
,  , значения декартовых координат
, значения декартовых координат
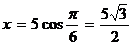 ,
,  .
.
Для выражения полярных координат через декартовы пользуются формулами
 ,
,  .
.
Чтобы найти из нее значение  , нужно учитывать, в какой координатной четверти лежит рассматриваемая точка М (x, y).
, нужно учитывать, в какой координатной четверти лежит рассматриваемая точка М (x, y).
Пример. Найти полярные координаты точки  .
.
Решение. Находим  ;
; 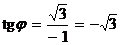 . Так как точка М лежит во второй четверти, то угол
. Так как точка М лежит во второй четверти, то угол  .
.
Ответ:  .
.



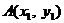 и
и  . Координаты точки
. Координаты точки  , делящей отрезок АВ в отношении
, делящей отрезок АВ в отношении 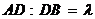 , определяются по формулам
, определяются по формулам ,
,  .
. , делящей отрезок АВ в отношении
, делящей отрезок АВ в отношении  ) находятся по формулам
) находятся по формулам ,
,  .
.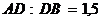 , если даны координаты точек
, если даны координаты точек 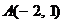 и
и  .
.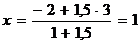 ,
,  .
.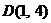 .
. ,
,  .
. .
. Окружность
Окружность  или
или 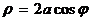 Рис. 8
Рис. 8
 Кардиоида
Кардиоида 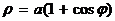 Рис. 9
Рис. 9
 Спираль Архимеда
Спираль Архимеда  Рис. 10
Рис. 10
 Лемниската Бернулли
Лемниската Бернулли  Рис. 11
Рис. 11
 .
. , а b – ордината точки пересечения прямой с осью Оу.
, а b – ордината точки пересечения прямой с осью Оу. имеем
имеем  – уравнение прямой, проходящей через начало координат.
– уравнение прямой, проходящей через начало координат.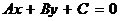
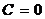 прямая проходит через начало координат;
прямая проходит через начало координат;
 уравнение примет вид
уравнение примет вид 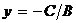 – прямая параллельна оси Ох (в частности,
– прямая параллельна оси Ох (в частности,  – уравнение самой оси Ох);
– уравнение самой оси Ох);
 уравнение примет вид
уравнение примет вид  – прямая параллельна оси Оу (в частности,
– прямая параллельна оси Оу (в частности, 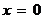 – уравнение самой оси Оу).
– уравнение самой оси Оу). можно получить уравнение
можно получить уравнение  , т.е. уравнение прямой с угловым коэффициентом
, т.е. уравнение прямой с угловым коэффициентом  .
. 2) подставляем в левую часть нормального уравнения прямой координаты
2) подставляем в левую часть нормального уравнения прямой координаты  ,
, 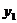 данной точки М.
данной точки М.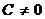 , т.е. если прямая не проходит через начало координат, то при
, т.е. если прямая не проходит через начало координат, то при  точка М и начало координат лежат по одну сторону от данной прямой, а при
точка М и начало координат лежат по одну сторону от данной прямой, а при  – по разные стороны (при
– по разные стороны (при  , очевидно, точка М лежит на прямой).
, очевидно, точка М лежит на прямой). до прямой
до прямой  .
. , поэтому
, поэтому  .
. .
. и
и  (т.е. длина отрезка АВ) равно
(т.е. длина отрезка АВ) равно 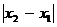 .
. , серединой отрезка АВ является точка
, серединой отрезка АВ является точка 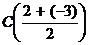 , т.е. точка
, т.е. точка  .
. числовой оси называется любой интервал, содержащий эту точку. В частности,
числовой оси называется любой интервал, содержащий эту точку. В частности, 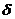 -окрестность точки
-окрестность точки  или множество чисел х, удовлетворяющих условию
или множество чисел х, удовлетворяющих условию 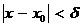 (где
(где  – координатами точек (см. рис. 1). Координата х называется абсциссой, а координата у – ординатой точки.
– координатами точек (см. рис. 1). Координата х называется абсциссой, а координата у – ординатой точки. и
и  (т.е. длина отрезка АВ) вычисляется по формуле
(т.е. длина отрезка АВ) вычисляется по формуле .
. .
. и полярный угол
и полярный угол  , где
, где  (где n – любое целое число).
(где n – любое целое число).
 , а полярный угол
, а полярный угол 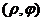 было взаимно однозначным, иногда ограничивают возможные значения полярного угла
было взаимно однозначным, иногда ограничивают возможные значения полярного угла  или
или  .
.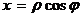 ,
, 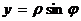
 ,
,  , значения декартовых координат
, значения декартовых координат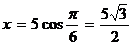 ,
,  .
. ,
,  .
. .
. ;
; 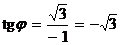 . Так как точка М лежит во второй четверти, то угол
. Так как точка М лежит во второй четверти, то угол  .
. .
.

