Нормальной генеральной совокупности.
Пусть по выборке объемом n из генеральной совокупности определены выборочное среднее значение m* и выборочное среднее квадратическое отклонение s. Кроме того задана требуемая надежность g.
Пусть также известно, что для выборки объема n из нормальной генеральной совокупности случайная величина:
 (8.5.1)
(8.5.1)
распределена по закону Стьюдента.
Здесь:
 - выборочное среднее (найденное по выборке);
- выборочное среднее (найденное по выборке);
s – выборочное среднее квадратическое отклонение;
m – истинное значение математического ожидания генеральной совокупности (измерений) при нормальном законе распределения случайной величины;
n – объем выборки.
Вероятность того, что математическое ожидание m входит в интервал, ограниченный значениями (8.5.1) равна:
 (8.5.2)
(8.5.2)
где fn-1(x) – плотность распределения вероятностей Стьюдента (функция четная);
Fn-1(x) – функция распределения случайной величины по закону Стьюдента с n-1 степенями свободы.
По таблице распределения Стьюдента (Приложение 8.2) с n-1 степенями свободы находим квантиль порядка  и получаем искомый доверительный интервал для m:
и получаем искомый доверительный интервал для m:

где W(A) – вероятность реализации события А.
Пример 8.5.1.
Произведено n=30 измерений концентрации газа в резервуаре перед его очисткой. Сделано предположение о нормальном распределении результатов измерений в генеральной совокупности. Выборочное среднее и выборочное среднее квадратическое отклонение соответственно равны:
 ,
, 
Требуется с достоверностью 0.95 определить интервал значений истинного математического ожидания концентрации газа в резервуаре.
Решение.
По таблице распределения Стьюдента (Приложение 8.2) находим квантиль порядка 0.975 для 29 степеней свободы:

Тогда значение искомого математического ожидания с требуемой надежностью находится в интервале:

Или вероятность того, что 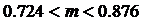 равна 0.95.
равна 0.95.
8.6. Доверительный интервал для среднего квадратического отклонения нормальной генеральной совокупности.
Если произведена выборка объемом n из генеральной совокупности, где по предположению случайная величина распределена по нормальному закону, вычислено выборочное среднее квадратическое отклонение s и задана требуемая надежность g, то соответствующий доверительный интервал, в котором содержится среднее квадратическое отклонение s, может быть определен с помощью c2 – распределения (Приложение 8.4) с n-1 степенями свободы порядков (1-g)/2 и (1+g)/2:
 (8.6.1)
(8.6.1)
Замечание. В знаменателе под знаком радикала не произведение c2 на (n-1), а c2 с (n-1) степенями свободы.
Пример 8.6.1.
По исходным данным примера 8.5.1 найти истинное среднее квадратическое отклонение концентрации газа в резервуаре.
По таблице распределения c2 находим соответствующие квантили:


Вычисляется доверительный интервал:
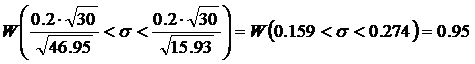
где W(А) – вероятность реализации события А.



 (8.5.1)
(8.5.1) - выборочное среднее (найденное по выборке);
- выборочное среднее (найденное по выборке); (8.5.2)
(8.5.2) и получаем искомый доверительный интервал для m:
и получаем искомый доверительный интервал для m:
 ,
, 


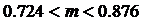 равна 0.95.
равна 0.95. (8.6.1)
(8.6.1)