Формула полной вероятности
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают.
Если событие может произойти с вероятностью и опыт повторяют раз, то вероятность, что оно наступит хотя бы один раз, есть:, где.
Если A1 + A2 +... + An = D,
т.е. если хотя бы одно из событий A1, A2,..., An непременно должно осуществиться, то говорят, что события A1, A2,..., An образуют полную группу событий.
Если при этом Ai попарно несовместимы (т. е. достоверное событие D подразделяется на частные случаи A1, A2,..., An), то говорят что события A1, A2,..., An образуют полную систему событий.
Таким образом, если A1, A2,..., An — полная система событий, то при каждом испытании обязательно происходит одно и только одно из событий A1, A2,..., An.
Пример. При бросании игральной кости события B, E2, E4, E6,, состоящие соответственно в выпадении нечетного числа очков, 2, 4 и 6 очков образуют полную систему.
Полную систему составляют также события E1, E2, E3, E4, E5, E6, со- стоящие соответственно в выпадении 1, 2, 3, 4, 5 и 6 очков.
9. Условная вероятность
Пусть и — зависимые события. Условной вероятностью события называется вероятность события, найденная в предположении, что событие уже наступило.
Теорема. Вероятность произведения двух зависимых событий и равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:.
Теорема. Вероятность суммы двух совместных событий и равна сумме вероятностей этих событий минус вероятность их произведения:.
Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.
Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.
10. Пусть вероятность события В не зависит от появления события А.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности: РA (В) = Р (В). (*)
Подставив (*) в соотношение (***) предыдущего параграфа, получим Р (A) Р (В) = Р (В) РB (A).
Отсюда РB (A) = Р (A), т. е. условная вероятность события A в предположении что наступило событие В, равна его безусловной вероятности. Другими словами, событие A не зависит от события В.
Итак, если событие В не зависит от события A, то событие A не зависит от события В; это означает, что с в о й с т в о н е з а в и с и м о с т и с о б ы т и й в з а и м н о.
Для независимых событий теорема умножения Р (АВ) = Р (А) РA (В) имеет вид Р (АВ) = Р (А) Р (В), (**)т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Равенство (**) принимают в качестве определения независимых событий. Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми. На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.
11. Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Р (A) = 1 — q 1 q 2... q n.(*)
Доказательство Обозначим через А событие, состоящее в появлении хотя бы одного из событий А1,А2,...,An. События А и
(ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:
Отсюда, пользуясь теоремой умножения, получим
или
Ч а с т н ы й с л у ч а й. Если события А1, А2,..., Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий P (A) = l — q n. (**)
12. теорема сложения для совместных событий
Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.
Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p (A + B)= p (A)+ p (B)− p (AB)
Доказательство:
A + B = AB + AB + AB (сумма несовместных пар)
Тогда p (A + B)= p (AB)+ p (AB)+ p (AB)
Событие A = AB + AB,
Событие B = AB + AB
p (A + B)= p (A)− p (AB)+ p (B)− p (AB)+ p (AB)= p (A)+ p (B)− p (AB)
Замечание: в этой теореме может существовать 2 различные ситуации.
p (A + B)= p (A)+ p (B)− p (A) p (B), где A и B - независимые;
p (A + B)= p (A)+ p (B)− p (A) p (B ∖ A), где A и B - зависимые;
13. Формула полной вероятности позволяет вычислить вероятность интересующего события через условные вероятности этого события в предположении неких гипотез, а также вероятностей этих гипотез.
Формулировка
Пусть дано вероятностное пространство, и полная группа попарно несовместных событий, таких что. Пусть — интересующее нас событие. Тогда.
Замечание
Формула полной вероятности также имеет следующую интерпретацию. Пусть N — случайная величина, имеющая распределение
.
Тогда, т.е. априорная вероятность события равна среднему его апостериорной вероятности.
14. Вероятность гипотез. Формулы Байеса
| Пусть событие А может наступить при условии появления одного из несовместных событий B1, B2,...,Bn образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности.
Допустим, что произведено испытание, в результате которого появилось событие А. Поставим своей задачей определить, как изменилось (в связи с тем, что событие А уже наступило) вероятность гипотез. Другими словами, будем искать условные вероятности:
PA(B1),PA(B2),...,PA(Bn)
Найдем сначала условную вероятность PA(B1). По теореме умножения имеем: P(AB1)=P(A)•PA(B1)=P(B1)•PB1(A) Отсюда. Заменив здесь Р(А) по формуле, получим:
Аналогично выводятся формулы, определяющие условные вероятности остальных гипотез, т.е. условная вероятность любой гипотезы Bi (i=1,2,...,n) может быть вычислена по формуле:
(*)
Формулу (*) называют формулой Байеса (от имени английского математика, который их вывел; опубликованы в 1764). Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
|
15. При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е., а вероятность противоположного события (событие А не наступило) - буквой.
Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли
Распределение числа успехов (появлений события) носит название биномиального распределения.
16. Локальная та интегральная теоремы Лапласа.
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых Р(А)= р, событие А состоится m раз, подается такой приближенной зависимостью:
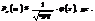
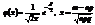
Локальная теорема Лапласа дает возможность вычислять вероятности, если n > 10 и p > 0,1.
17. Интегральная теорема Лапласа. Вероятность того, что событие А состоится от 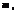 к раз при проведении n независимых испытаний, в каждом из которых событие А происходит с вероятностью р, подается формулой:
к раз при проведении n независимых испытаний, в каждом из которых событие А происходит с вероятностью р, подается формулой:
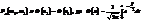 —функція Лапласа;
—функція Лапласа;
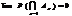
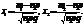
Значения функции Лапласа наводятся в специальных таблицах.
Плотность распределения
Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.
Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.
Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.
Определение. Случайная величина Х называется непрерывной, если ее функция распределенияF(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением(может быть, конечного числа точек.
Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.
Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.
№ 31. Равномерное распределение НСВ: ф-я распр-я, плотность расп-я, график, мат ожидание, дисперсия
Функция надежности
Будем называть элементом некоторое устройство независимо от того, "простое" оно или "сложное".
Пусть элемент начинает работать в момент времени t0=0, а по истечении времени длительностью t происходит отказ. Обозначим через Т непрерывную случайную величину - длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t то, следовательно, за время длительностью t наступит отказ.
Таким образом, функция распределения F (t)=P(T<t) определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т. е. вероятность противоположного события Т > t, равна 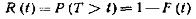
Функцией надежности R (t) называют функцию, определяющую надежность работы элемента за время длительностью t:
Свойства функции расп-я
1.Значения ф-и расп-я удовлетв. Неравенству 0< F(x;y)<1
2. Ф-я F(x;y) явл. Неубывающей ф-ей.
3. Имеют место след соотношения:1)F(-∞; y)=0 2) F(x;-∞)=0 3) F(-∞;-∞)=0 4) F(+∞;+∞)=1
4. При у=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей х. При х=∞, ф-я расп-я с-мы становиться ф-ей расп-я составляющей у
№ 45 Система двух случайных величин: плотность совместного расп-я вероятностей, нахождение ф-и расп-я по плотности расп-я, свойства двумерной плотности расп-я
Плотность совм.расп-я вероятностей назв частную производную второго порядка, смешанная по переменным х, у
Доверительный интервал
Доверительный интервал - это допустимое отклонение наблюдаемых значений от истинных. Размер этого допущения определяется исследователем с учетом требований к точности информации. Если увеличивается допустимая ошибка, размер выборки уменьшается, даже если уровень доверительной вероятности останется равным 95%.
Доверительный интервал показывает, в каком диапазоне расположатся результаты выборочных наблюдений (опросов). Если мы проведем 100 одинаковых опросов в одинаковых выборках из единой генеральной совокупности (например, 100 выборок по 1000 человек в каждой в городе с населением 5 миллионов человек), то при 95%-й доверительной вероятности, 95 из 100 результатов попадут в пределы доверительного интервала (например, от 28% до 32% при истинном значении 30%).
53. ТОЧЕЧНАЯ ОЦЕНКА
- статистическая оценка, значения к-рой суть точки во множестве значений оцениваемой величины.
Пусть по реализации 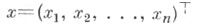 случайного вектора
случайного вектора 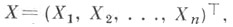 принимающего значения в выборочном пространстве
принимающего значения в выборочном пространстве 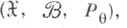
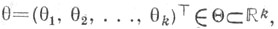 надлежит оценить неизвестный параметр
надлежит оценить неизвестный параметр 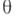 (или нек-рую функцию
(или нек-рую функцию  Тогда любая статистика Т n=Т п (Х), осуществляющая отображение множества
Тогда любая статистика Т n=Т п (Х), осуществляющая отображение множества 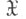 в
в 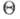 (или в множество значений функции
(или в множество значений функции 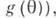 наз. точечной оценкой параметра
наз. точечной оценкой параметра 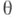 (оцениваемой функции
(оцениваемой функции 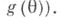 Важными характеристиками Т. о. Т п являются ее математич. ожидание
Важными характеристиками Т. о. Т п являются ее математич. ожидание
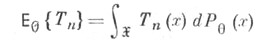
и дисперсионная матрица (ковариационная матрица)
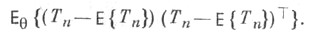
Вектор 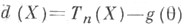 наз. вектором ошибок Т. о. Т п. Если
наз. вектором ошибок Т. о. Т п. Если
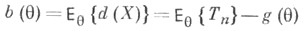
- нулевой вектор при всех  то говорят, что Т п является несмещенной оценкой функции
то говорят, что Т п является несмещенной оценкой функции 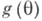 или что Т п лишена систематич. ошибки, в противном случае Т. о. Т п наз. смещенной, а вектор
или что Т п лишена систематич. ошибки, в противном случае Т. о. Т п наз. смещенной, а вектор 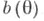 - смещением или систематической ошибкой Т. <о. Качество Т. о. определяется с помощью функции риска.
- смещением или систематической ошибкой Т. <о. Качество Т. о. определяется с помощью функции риска.
Введем понятие интервальной оценки неизвестного параметра
генеральной совокупности (или случайной величины, определенной на
множестве объектов этой генеральной совокупности). Обозначим этот
параметр через. По сделанной выборке по определенным правилам
найдем числа 1 и 2, так чтобы выполнялось условие:
P(1< < 2) =P ((1; 2)) =
Числа 1 и 2 называются доверительными границами, интервал (1, 2)
— доверительным интервалом для параметра. Число называется
доверительной вероятностью или надежностью сделанной оценки.
Сначала задается надежность. Обычно ее выбирают равной 0.95,
0.99 или 0.999. Тогда вероятность того, что интересующий нас параметр
попал в интервал (1, 2) достаточно высока. Число (1 + 2) / 2 – середина
доверительного интервала – будет давать значение параметра с
точностью (2 – 1) / 2, которая представляет собой половину длины
доверительного интервала.
Границы 1 и 2 определяются из выборочных данных и являются
функциями от случайных величин x1, x2,..., xn
, а следовательно – сами
случайные величины. Отсюда – доверительный интервал (1, 2) тоже
случаен. Он может покрывать параметр или нет. Именно в таком смысле
нужно понимать случайное событие, заключающееся в том, что
доверительный интервал покрывает число
54. Выборочный коэффициент корреляции рассчитывается по формуле
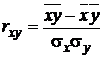
Здесь
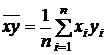 ,
, 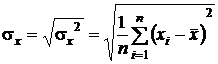 ,
,
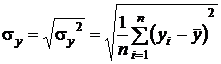 .
.
Выборочный коэффициент корреляции можно рассматривать как точечную оценку коэффициента корреляции rxh, характеризующего генеральную совокупность.
Ошибки I и II рода..
При проверке гипотез могут быть совершены ошибки 2-х родов:
1) Ошибкой I рода наз. такая ошибка, кот. совершается, если будет отвергнута правильная нулевая гипотеза. Вероятность ошибки I рода обозначается a и наз. уровнем значимости:
a £ 0,1
Отклонения нулевой гип. на уровне a = 0,05 означ, что мы не ошибаемся в 95 случаях из 100 или совершаем всё таки ошибку, принимая правильную гипотезу за ложную в 5 случаях из 100.
2) Ошибка II рода состоит в том, что будет принята неправильная нулевая гипотеза H0 . Вер-сть ошибки II рода обозначается b.
Стат. критерием (значимости) наз. СВ X, кот. является ф-цией выборки K=К(х1, х2, х3,…,хn) (статистической) и служит для проверки гипотезы, с ее помощью принимается решение о принятии или отвержении гипотезы Н0.
Критическая область – совок – ть значений критерия, при которых нулевую гипотезу отвергают.
Точки, разделяющие критическую область и область допустимых значений, называются критическими точками (или границами критической области).
57. Мощностью критерия k наз. вер-сть М несовершения ошибки II рода: М= 1-b. Др. словами, мощность критерия – это вер-сть того, что нулевая гип. будет отвергнута, если верна конкурируюшая гип. H1.
 Если n®¥, b®1, то критерий наз. критерием согласия.
Если n®¥, b®1, то критерий наз. критерием согласия.
При данном уровне значимости a из всех критериев лучшим будет тот, у кот. вер-сть ошибки II рода b будет минимальной.
 После выбора критерия k множ-во всех его значений распадается на 2 непересекающихся подмножеств: критическую область W и О.Д.З. (или обл. принятия гипотезы).
После выбора критерия k множ-во всех его значений распадается на 2 непересекающихся подмножеств: критическую область W и О.Д.З. (или обл. принятия гипотезы).
ОДЗ W

 k Если значение критерия kнабл. попадает в критич.
k Если значение критерия kнабл. попадает в критич.
область, то нулевая гипотеза отвергается в пользу конкурирующей гип. H1. Если kнабл. попадает в О.Д.З., то нет оснований отвергнуть нулевую гипотезу, т.е. рез-ты опыта согласовываются с гипотезой.
| Отыскание правосторонней критической области
|
Как найти критическую область? Для определения начнем с нахождения правосторонней критической области, которая определяется неравенством К > Ккр, где Ккр > 0.
Для отыскания правосторонней критической области достаточно найти критическую точку. Следовательно, возникает новый вопрос: как ее найти?
С этой целью задаются достаточно малой вероятностью – уровнем значимости. Затем ищут критическую точку Ккр, исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий К примет значение, большее Ккр, была равна принятому значению уровня значимости: Р (К > Ккр) = 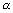 .
Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию.
Когда критическая точка уже найдена, вычисляют по данным выборок наблюденное значение критерия и, если окажется, что
Кнабл > Ккр, то нулевую гипотезу отвергают; если же Кнабл < Ккр, то нет оснований, чтобы отвергнуть нулевую гипотезу.
Почему правосторонняя критическая область была определена, исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение Р (К > Ккр) = .
Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию.
Когда критическая точка уже найдена, вычисляют по данным выборок наблюденное значение критерия и, если окажется, что
Кнабл > Ккр, то нулевую гипотезу отвергают; если же Кнабл < Ккр, то нет оснований, чтобы отвергнуть нулевую гипотезу.
Почему правосторонняя критическая область была определена, исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение Р (К > Ккр) = 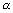 .
Поскольку вероятность события К > Ккр мала ( .
Поскольку вероятность события К > Ккр мала ( 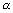 – малая вероятность), такое событие при справедливости нулевой гипотезы в силу принципа практической невозможности маловероятных событий в единичном испытании не должно наступить. Если все же оно произошло, т. е. наблюдаемое значение критерия оказалось больше Ккр, то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование Р (К > Ккр) = – малая вероятность), такое событие при справедливости нулевой гипотезы в силу принципа практической невозможности маловероятных событий в единичном испытании не должно наступить. Если все же оно произошло, т. е. наблюдаемое значение критерия оказалось больше Ккр, то это можно объяснить тем, что нулевая гипотеза ложна и, следовательно, должна быть отвергнута. Таким образом, требование Р (К > Ккр) = 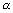 определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они составляют правостороннюю критическую область.
Наблюдаемое значение критерия может оказаться большим Ккр не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости определяет такие значения критерия, при которых нулевая гипотеза отвергается, а они составляют правостороннюю критическую область.
Наблюдаемое значение критерия может оказаться большим Ккр не потому, что нулевая гипотеза ложна, а по другим причинам (малый объем выборки, недостатки методики эксперимента и др.). В этом случае, отвергнув правильную нулевую гипотезу, совершают ошибку первого рода. Вероятность этой ошибки равна уровню значимости 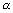 . .
|
| Отыскание левосторонней и двусторонней критических областей
|
Отыскание левосторонней и двусторонней критических областей сводится (так же как и для правосторонней) к нахождению соответствующих критических точек.
Левосторонняя критическая область определяется неравенством:
К < Ккр (Ккр < 0).
Критическую точку находят, исходя из требования, чтобы при справедливости нулевой гипотезы вероятность того, что критерий имеет значение, меньшее Ккр, была равна принятому уровню значимости: Р (К < Ккр) = 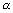 .
Двусторонняя критическая область определяется неравенствами:
К< К1, К > К2.
Критические точки находят, исходя из требования, чтобы при справедливости нулевой гипотезы сумма вероятностей того, что критерий примет значение, меньшее К1 и большее К2, была равна принятому уровню значимости: Р (К < К1) + Р (К > К2) = .
Двусторонняя критическая область определяется неравенствами:
К< К1, К > К2.
Критические точки находят, исходя из требования, чтобы при справедливости нулевой гипотезы сумма вероятностей того, что критерий примет значение, меньшее К1 и большее К2, была равна принятому уровню значимости: Р (К < К1) + Р (К > К2) = 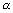 .
Ясно, что критические точки могут быть выбраны множеством способов. Если распределение критерия симметрично относительно нуля и имеются основания выбирать симметричные относительно нуля точки Ккр и Ккр (К > 0), то Р (К < -Ккр) = Р (К > Ккр).
Зная Р (К < К1) + Р (К > К2) = .
Ясно, что критические точки могут быть выбраны множеством способов. Если распределение критерия симметрично относительно нуля и имеются основания выбирать симметричные относительно нуля точки Ккр и Ккр (К > 0), то Р (К < -Ккр) = Р (К > Ккр).
Зная Р (К < К1) + Р (К > К2) = 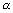 , получим Р (К > Ккр) = , получим Р (К > Ккр) = 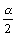 .
Это соотношение и служит для отыскания критических точек двусторонней критической области. Критические точки находят по соответствующим таблицам. .
Это соотношение и служит для отыскания критических точек двусторонней критической области. Критические точки находят по соответствующим таблицам.
|
58.. Критерий Фишера.
Критерий используется для сравнения дисперсий двух выборок с нормальным распределением.
Сравнения дисперсий двух выборок производятся по отношению большей по величине дисперсии(записывается в числителе) к меньшей (записывается в знаменателе). Поэтому значения критерия больше или равно 1,0.
Гипотезы
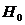 : Дисперсия выборке 1 не отличается от дисперсии в выборке 2
: Дисперсия выборке 1 не отличается от дисперсии в выборке 2
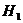 : Дисперсия выборке 1 отличается от дисперсии в выборке 2
: Дисперсия выборке 1 отличается от дисперсии в выборке 2
Ограничения
Данные в выборках должны быть измерены по шкале интервалов или по шкале отношений.
Обе сравниваемые выборки должны иметь нормальный закон распределения.
Алгоритм.
- Предварительно проверяется нормальность закона распределения по одному из критериев согласия.
- Рассчитывается средне арифметические значения
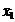 и
и 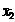 для каждой выборки по формуле
для каждой выборки по формуле 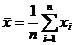 где
где 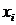 – значение i -го результата наблюдения
– значение i -го результата наблюдения - Рассчитываются значение
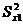 и
и 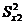 –дисперсии для каждой выборке по формуле
–дисперсии для каждой выборке по формуле 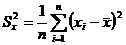
- Определяется число степеней свободы по выборкам:
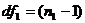 - по первой выборке и
- по первой выборке и 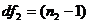 по второй выборке.
по второй выборке.
- Рассчитывается
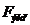 - эмпирическое значение критерия по одной из формул:
- эмпирическое значение критерия по одной из формул:
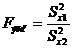 или
или 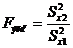 с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.
с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.
- Найденное эмпирическое значение критерия Фишера
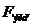 сравнивается критическим значением
сравнивается критическим значением 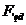 (по таблице 2 приложения) для данного числа степеней свободы
(по таблице 2 приложения) для данного числа степеней свободы 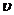 .
.
Если эмпирическое значение 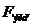 <
< 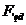 , то нулевая гипотеза
, то нулевая гипотеза 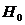 о равенстве дисперсий в выборках при заданном уровне значимости
о равенстве дисперсий в выборках при заданном уровне значимости 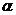 принимается.
принимается.
59. Проверка гипотез о законе распределения (критерии Пирсона)
Существует несколько критериев согласия для проверки законов распределения случайной величины. Это критерии Колмогорова, Смирнова, Пирсона и др. Мы остановимся лишь на критерии Пирсона это наиболее часто употребляемый критерий для проверки закона распределения случайной величины.
Достоинством критерия Пирсона является его универсальность: с его помощью можно проверять гипотезы о различных законах распределения.
Проверка гипотезы о нормальном распределении.
Пусть получена выборка достаточно большого объема п с большим количеством различных значений вариант. Доя удобства ее обработки разделим интервал от наименьшего до наибольшего из значений вариант на s равных частей и будем считать, что значения вариант, попавших в каждый интервал, приближенно равны числу, задающему середину интервала. Подсчитав число вариант, попавших в каждый интервал, составим так называемую сгруппированную выборку:
варианты..х1 х2 хs
частоты.п1 п2 пs,
где хi значения середин интервалов, а пi число вариант, попавших в i-й интервал (эмпирические частоты).
По полученным данным можно вычислить выборочное среднее и выборочное среднее квадратическое отклонение?В. Проверим предположение, что генеральная совокупность распределена по нормальному закону с параметрами M(X) =, D(X) =. Тогда можно найти количество чисел из выборки объема п, которое должно оказаться в каждом интервале при этом предположении (то есть теоретические частоты). Для этого по таблице значений функции Лапласа найдем вероятность попадания в i-й интервал:
,
где аi и bi- границы i-го интервала. Умножив полученные вероятности на объем выборки п, найдем теоретические частоты: пi =n?pi. Наша цель сравнить эмпирические и теоретические частоты, которые, конечно, отличаются друг от друга, и выяснить, являются ли эти различия несущественными, не опровергающими гипотезу о нормальном распределении исследуемой случайной величины, или они настолько велики, что противоречат этой гипотезе. Для этого используется критерий в виде случайной величины
. (1)
Смысл ее очевиден: суммируются части, которые квадраты отклонений эмпирических частот от теоретических составляют от соответствующих теоретических частот. Можно доказать, что вне зависимости от реального закона распределения генеральной совокупности закон распределения случайной величины (1) при стремится к закону распределения с числом степеней свободы k = s 1 r, где r число параметров предполагаемого распределения, оцененных по данным выборки. Нормальное распределение характеризуется двумя параметрами, поэтому k = s 3. Для выбранного критерия строится правосторонняя критическая область, определяемая условием
(2)
где? уровень значимости. Следовательно, критическая область задается неравенством а область принятия гипотезы -.
Итак, для проверк
Формула полной вероятности
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Вероятности противоположных событий в сумме дают.
Если событие может произойти с вероятностью и опыт повторяют раз, то вероятность, что оно наступит хотя бы один раз, есть:, где.
Если A1 + A2 +... + An = D,
т.е. если хотя бы одно из событий A1, A2,..., An непременно должно осуществиться, то говорят, что события A1, A2,..., An образуют полную группу событий.
Если при этом Ai попарно несовместимы (т. е. достоверное событие D подразделяется на частные случаи A1, A2,..., An), то говорят что события A1, A2,..., An образуют полную систему событий.
Таким образом, если A1, A2,..., An — полная система событий, то при каждом испытании обязательно происходит одно и только одно из событий A1, A2,..., An.
Пример. При бросании игральной кости события B, E2, E4, E6,, состоящие соответственно в выпадении нечетного числа очков, 2, 4 и 6 очков образуют полную систему.
Полную систему составляют также события E1, E2, E3, E4, E5, E6, со- стоящие соответственно в выпадении 1, 2, 3, 4, 5 и 6 очков.
9. Условная вероятность
Пусть и — зависимые события. Условной вероятностью события называется вероятность события, найденная в предположении, что событие уже наступило.
Теорема. Вероятность произведения двух зависимых событий и равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:.
Теорема. Вероятность суммы двух совместных событий и равна сумме вероятностей этих событий минус вероятность их произведения:.
Теорема. (Умножения вероятностей) Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило.
Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события.
10. Пусть вероятность события В не зависит от появления события А.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности: РA (В) = Р (В). (*)
Подставив (*) в соотношение (***) предыдущего параграфа, получим Р (A) Р (В) = Р (В) РB (A).
Отсюда РB (A) = Р (A), т. е. условная вероятность события A в предположении что наступило событие В, равна его безусловной вероятности. Другими словами, событие A не зависит от события В.
Итак, если событие В не зависит от события A, то событие A не зависит от события В; это означает, что с в о й с т в о н е з а в и с и м о с т и с о б ы т и й в з а и м н о.
Для независимых событий теорема умножения Р (АВ) = Р (А) РA (В) имеет вид Р (АВ) = Р (А) Р (В), (**)т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Равенство (**) принимают в качестве определения независимых событий. Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми. На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.
11. Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.
Теорема. Вероятность появления хотя бы одного из событий А1, А2,..., Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Р (A) = 1 — q 1 q 2... q n.(*)
Доказательство Обозначим через А событие, состоящее в появлении хотя бы одного из событий А1,А2,...,An. События А и
(ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:
Отсюда, пользуясь теоремой умножения, получим
или
Ч а с т н ы й с л у ч а й. Если события А1, А2,..., Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий P (A) = l — q n. (**)
12. теорема сложения для совместных событий
Суммой 2-х совместных событий называют событие, состоящее в появлении либо события A, либо события B, либо обоих сразу.
Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p (A + B)= p (A)+ p (B)− p (AB)
Доказательство:
A + B = AB + AB + AB (сумма несовместных пар)
Тогда p (A + B)= p (AB)+ p (AB)+ p (AB)
Событие A = AB + AB,
Событие B = AB + AB
p (A + B)= p (A)− p (AB)+ p (B)− p (AB)+ p (AB)= p (A)+ p (B)− p (AB)
Замечание: в этой теореме



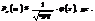
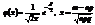
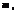 к раз при проведении n независимых испытаний, в каждом из которых событие А происходит с вероятностью р, подается формулой:
к раз при проведении n независимых испытаний, в каждом из которых событие А происходит с вероятностью р, подается формулой: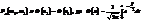 —функція Лапласа;
—функція Лапласа;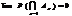
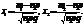
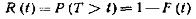
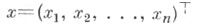 случайного вектора
случайного вектора 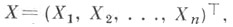 принимающего значения в выборочном пространстве
принимающего значения в выборочном пространстве 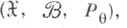
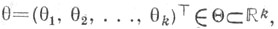 надлежит оценить неизвестный параметр
надлежит оценить неизвестный параметр 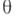 (или нек-рую функцию
(или нек-рую функцию  Тогда любая статистика Т n=Т п (Х), осуществляющая отображение множества
Тогда любая статистика Т n=Т п (Х), осуществляющая отображение множества 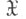 в
в 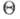 (или в множество значений функции
(или в множество значений функции 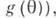 наз. точечной оценкой параметра
наз. точечной оценкой параметра 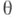 (оцениваемой функции
(оцениваемой функции 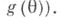 Важными характеристиками Т. о. Т п являются ее математич. ожидание
Важными характеристиками Т. о. Т п являются ее математич. ожидание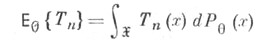
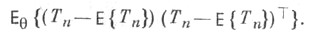
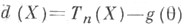 наз. вектором ошибок Т. о. Т п. Если
наз. вектором ошибок Т. о. Т п. Если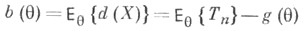
 то говорят, что Т п является несмещенной оценкой функции
то говорят, что Т п является несмещенной оценкой функции 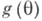 или что Т п лишена систематич. ошибки, в противном случае Т. о. Т п наз. смещенной, а вектор
или что Т п лишена систематич. ошибки, в противном случае Т. о. Т п наз. смещенной, а вектор 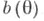 - смещением или систематической ошибкой Т. <о. Качество Т. о. определяется с помощью функции риска.
- смещением или систематической ошибкой Т. <о. Качество Т. о. определяется с помощью функции риска.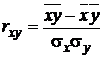
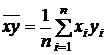 ,
, 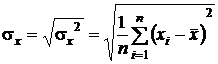 ,
,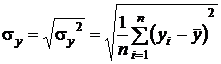 .
. Если n®¥, b®1, то критерий наз. критерием согласия.
Если n®¥, b®1, то критерий наз. критерием согласия. После выбора критерия k множ-во всех его значений распадается на 2 непересекающихся подмножеств: критическую область W и О.Д.З. (или обл. принятия гипотезы).
После выбора критерия k множ-во всех его значений распадается на 2 непересекающихся подмножеств: критическую область W и О.Д.З. (или обл. принятия гипотезы).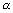 .
Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию.
Когда критическая точка уже найдена, вычисляют по данным выборок наблюденное значение критерия и, если окажется, что
Кнабл > Ккр, то нулевую гипотезу отвергают; если же Кнабл < Ккр, то нет оснований, чтобы отвергнуть нулевую гипотезу.
Почему правосторонняя критическая область была определена, исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение Р (К > Ккр) =
.
Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию.
Когда критическая точка уже найдена, вычисляют по данным выборок наблюденное значение критерия и, если окажется, что
Кнабл > Ккр, то нулевую гипотезу отвергают; если же Кнабл < Ккр, то нет оснований, чтобы отвергнуть нулевую гипотезу.
Почему правосторонняя критическая область была определена, исходя из требования, чтобы при справедливости нулевой гипотезы выполнялось соотношение Р (К > Ккр) = 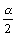 .
Это соотношение и служит для отыскания критических точек двусторонней критической области. Критические точки находят по соответствующим таблицам.
.
Это соотношение и служит для отыскания критических точек двусторонней критической области. Критические точки находят по соответствующим таблицам.
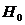 : Дисперсия выборке 1 не отличается от дисперсии в выборке 2
: Дисперсия выборке 1 не отличается от дисперсии в выборке 2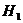 : Дисперсия выборке 1 отличается от дисперсии в выборке 2
: Дисперсия выборке 1 отличается от дисперсии в выборке 2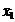 и
и 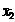 для каждой выборки по формуле
для каждой выборки по формуле 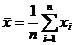 где
где 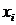 – значение i -го результата наблюдения
– значение i -го результата наблюдения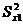 и
и 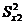 –дисперсии для каждой выборке по формуле
–дисперсии для каждой выборке по формуле 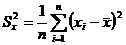
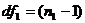 - по первой выборке и
- по первой выборке и 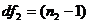 по второй выборке.
по второй выборке.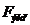 - эмпирическое значение критерия по одной из формул:
- эмпирическое значение критерия по одной из формул: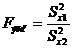 или
или 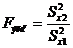 с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.
с учетом того, что дисперсия в числителе должна быть больше дисперсии в знаменателе.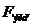 сравнивается критическим значением
сравнивается критическим значением 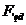 (по таблице 2 приложения) для данного числа степеней свободы
(по таблице 2 приложения) для данного числа степеней свободы 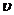 .
.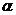 принимается.
принимается.


