Свойства сходящихся числовых рядов
1°. Пусть ряд 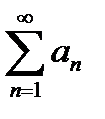 сходится и
сходится и 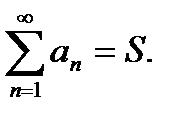 Тогда для любого
Тогда для любого 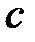 (
(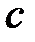 = const) сходится ряд
= const) сходится ряд 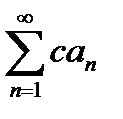 и имеет сумму
и имеет сумму 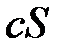 .{Пусть
.{Пусть 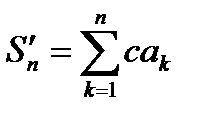 .
. 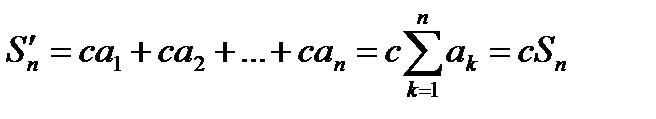 ,
, 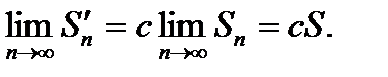 }.
}.
2°. Если сходятся ряды 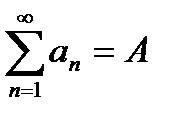 и
и 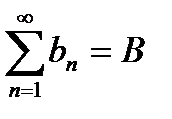 , то сходится ряд
, то сходится ряд 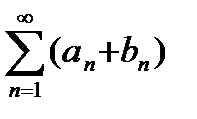 и имеет сумму A+B.
и имеет сумму A+B.
{Пусть 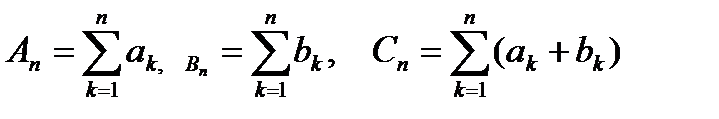 . =>
. => 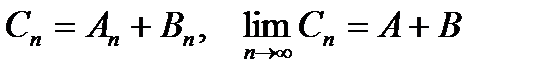 }.
}.
3°. Если 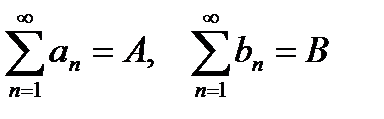 , то для любых чисел
, то для любых чисел  и
и 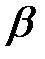
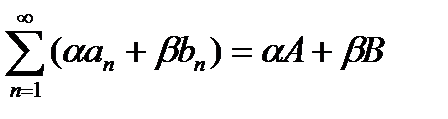 . {Следует из 1° и 2°}
. {Следует из 1° и 2°}
4°. Если сходится ряд 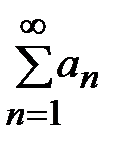 , то сходится и любой его остаток. Если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
, то сходится и любой его остаток. Если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
{Обозначим m-ый остаток ряда  , его p-ую частичную сумму
, его p-ую частичную сумму 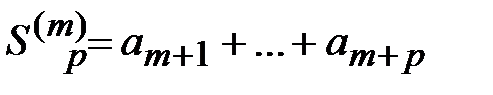 . Пусть
. Пусть 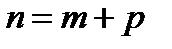 .
. 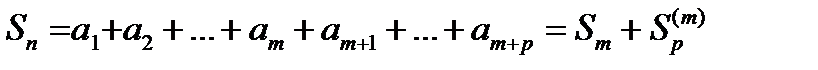 ;
; 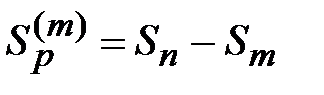 (*) Зафиксируем
(*) Зафиксируем 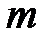 , а
, а 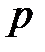 устремим к бесконечности. Тогда
устремим к бесконечности. Тогда 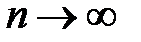 .
. 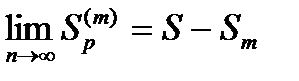 и остаток ряда
и остаток ряда 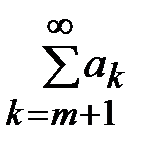 сходится.
сходится.
Если же известно, что сходится остаток ряда  , то из (*) следует:
, то из (*) следует: 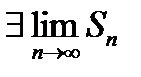 и ряд
и ряд 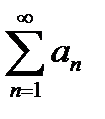 сходится.
сходится.
Обозначим 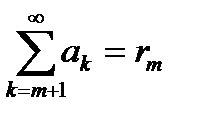 . Тогда из (*) следует:
. Тогда из (*) следует:  (**) или
(**) или 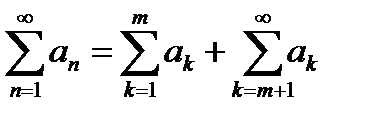 .} Выводы: 1. Переходя в (**) к пределу при
.} Выводы: 1. Переходя в (**) к пределу при 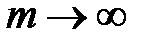 , получаем
, получаем 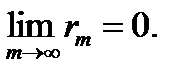 2.Отбрасывание конечного числа начальных членов ряда или присоединение в начале его нескольких новых членов не отражается на поведении ряда (в смысле его сходимости или расходимости).
2.Отбрасывание конечного числа начальных членов ряда или присоединение в начале его нескольких новых членов не отражается на поведении ряда (в смысле его сходимости или расходимости).
Критерий Коши сходимости числовых рядов. Необходимое условие сходимости
Теорема (критерий Коши): Для того чтобы ряд 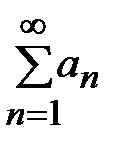 сходился, необходимо и достаточно, чтобы
сходился, необходимо и достаточно, чтобы  и
и 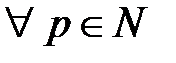 выполнялось бы:
выполнялось бы:  .{Сходимость числового ряда определяется сходимостью числовой последовательности {
.{Сходимость числового ряда определяется сходимостью числовой последовательности {  }. Ранее доказано: для того чтобы последовательность {
}. Ранее доказано: для того чтобы последовательность {  } сходилась, необходимо и достаточно, чтобы
} сходилась, необходимо и достаточно, чтобы  и
и  выполнялось бы:
выполнялось бы: 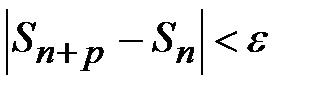 или
или  .}
.}
Теорема (необходимое условие сходимости):  . Переходя к пределу при
. Переходя к пределу при 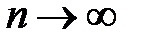 , получим:
, получим:  . Тот же результат можно получить из критерия Коши, полагая p = 1. Очевидно, условие
. Тот же результат можно получить из критерия Коши, полагая p = 1. Очевидно, условие  является необходимым, но не достаточным условием сходимости числового ряда. (НО: Ряд
является необходимым, но не достаточным условием сходимости числового ряда. (НО: Ряд  расходится, однако
расходится, однако  )
)
Признаки сравнения числовых рядов
Теорема 1 (признак сравнения): Пусть даны два ряда:  (1) и
(1) и  (2). Если, начиная с некоторого номера выполняется:
(2). Если, начиная с некоторого номера выполняется:  (3),
(3),  , то из сходимости ряда (2)
, то из сходимости ряда (2)  сходимость ряда (1); из расходимости ряда (1)
сходимость ряда (1); из расходимости ряда (1)  расходимость ряда (2).
расходимость ряда (2).
{ Не ограничивая общности, будем считать, что неравенство  выполняется для всех n. Пусть
выполняется для всех n. Пусть  . Очевидно, последовательности {
. Очевидно, последовательности { 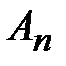 } и {
} и { 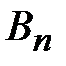 } – монотонные неубывающие. Пусть ряд (2) сходится. Тогда {
} – монотонные неубывающие. Пусть ряд (2) сходится. Тогда {  } ограничена:
} ограничена:  . Но тогда, в силу (3),
. Но тогда, в силу (3),  и ряд (1) – также сходится.
и ряд (1) – также сходится.
Пусть ряд (1) расходится. Если бы ряд (2) сходился, то, по доказанному выше, сходился бы и ряд (1). Т.е. получили бы противоречие. Таким образом, ряд (2) также расходится.}
Теорема 2 (признак сравнения в предельной форме): Пусть  Если существует
Если существует  то ряды (1) и (2) сходятся либо расходятся одновременно. { Пусть ряд (2) сходится.Из существования
то ряды (1) и (2) сходятся либо расходятся одновременно. { Пусть ряд (2) сходится.Из существования  :
:  , откуда получаем:
, откуда получаем:  или
или  следует сходимость ряда (1). Пусть ряд (2) расходится.Существует
следует сходимость ряда (1). Пусть ряд (2) расходится.Существует  , откуда аналогичным образом получаем:
, откуда аналогичным образом получаем: 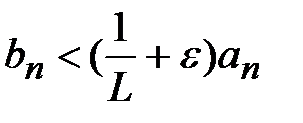 . Если бы сходился ряд (1), а вместе с ним и ряд
. Если бы сходился ряд (1), а вместе с ним и ряд  , то по теореме 1 сходился бы и ряд (2). А это не так. Значит, ряд (1) также расходится.}
, то по теореме 1 сходился бы и ряд (2). А это не так. Значит, ряд (1) также расходится.}
 . Так как
. Так как  , а ряд
, а ряд  - расходится (
- расходится ( то расходится и ряд
то расходится и ряд  .
.
Признак Коши и Даламбера
Теорема (признак Коши в предельной форме): Если существует  , то при
, то при  ряд (1) сходится; при
ряд (1) сходится; при  расходится, при
расходится, при  этот признак не даёт возможности судить о поведении ряда.
этот признак не даёт возможности судить о поведении ряда.
{ 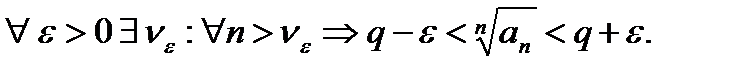
a)  начиная с некоторого номера
начиная с некоторого номера  <
<  1. Ряд сходится.
1. Ряд сходится.
б) 
 начиная с некоторого номера
начиная с некоторого номера  >1. Ряд расходится. }
>1. Ряд расходится. }
Теорема (признак Даламбера): Пусть  Если, начиная с некоторого номера
Если, начиная с некоторого номера 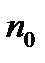 ,
,  для всех
для всех  , то ряд (1) сходится. Если же
, то ряд (1) сходится. Если же  , то ряд (1) расходится. { Пусть
, то ряд (1) расходится. { Пусть  . Для
. Для 
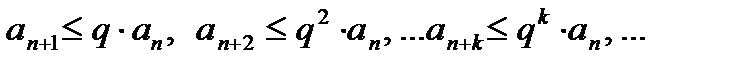 Т.к. ряд
Т.к. ряд  - сходится, то, по признаку сравнения, сходится и остаток ряда
- сходится, то, по признаку сравнения, сходится и остаток ряда  , а значит, сходится ряд
, а значит, сходится ряд  (1). Пусть для
(1). Пусть для 
 . Т.е.
. Т.е. 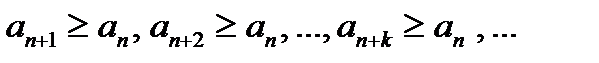 и
и  , не выполняется необходимое условие сходимости ряда. Ряд расходится. }
, не выполняется необходимое условие сходимости ряда. Ряд расходится. }
Теорема (признак Даламбера в предельной форме): Если 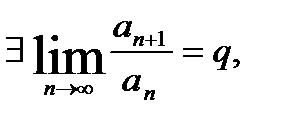 то при
то при  ряд (1) сходится, при
ряд (1) сходится, при  расходится, при
расходится, при  этот признак не даёт возможности судить о поведении ряда.
этот признак не даёт возможности судить о поведении ряда.
{  a)
a)  начиная с некоторого номера
начиная с некоторого номера  Ряд сх.
Ряд сх.
б) 
 начиная с некоторого номера
начиная с некоторого номера  >1. Ряд расх. }
>1. Ряд расх. }
5.Интегральный признак сходимости (Признак Коши - Маклорена)
Теорема (Коши - Маклорена): Пусть функция у = f(x) определена при х≥1, неотрицательна и монотонно убывает на 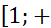 ∞). Тогда ряд
∞). Тогда ряд  , где
, где  сходится тогда и только тогда, когда сходится несобственный интеграл
сходится тогда и только тогда, когда сходится несобственный интеграл  (2)
(2)
[Так как f(x) монотонна на 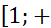 ∞), то она интегрируема по Риману на любом отрезке [1,
∞), то она интегрируема по Риману на любом отрезке [1,  ], поэтому имеет смысл
], поэтому имеет смысл  . Так как f(x)-убывает на
. Так как f(x)-убывает на 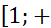 ∞), то для
∞), то для  f(k+1)
f(k+1)  . Проинтегрируем последнее неравенство по отрезку
. Проинтегрируем последнее неравенство по отрезку  :
:  , k=1,2,3.4...
, k=1,2,3.4...
Просуммируем по к:
 Обозначим,
Обозначим,  Тогда
Тогда

Пусть несобственный интеграл (2) сходится. Последовательность  монотонна (
монотонна ( ) и ограничена. Тогда ограничена и последовательность
) и ограничена. Тогда ограничена и последовательность  . А поскольку она монотонно возрастает, то является сходящейся.
. А поскольку она монотонно возрастает, то является сходящейся.
Пусть сходится ряд (1). Покажем, что сходится несобственный интеграл (2). Последовательность  – монотонная, сходящаяся последовательность, следовательно, ограничена.
– монотонная, сходящаяся последовательность, следовательно, ограничена.
Тогда из (3) следует ограниченность возрастающей последовательности  , а следовательно, её сходимость. То есть существует конечный
, а следовательно, её сходимость. То есть существует конечный  ; интеграл (2) сходится.}
; интеграл (2) сходится.}
Пример:  , s>0, Рассмотрим f(x)=
, s>0, Рассмотрим f(x)=  на [1,
на [1, 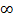 );
);

Значит, ряд сходится при s>1 и расходится при s 
Следствие.
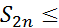 S
S 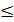 S2n-1
S2n-1
S- 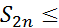 S2n+1-S2n =
S2n+1-S2n =  , S2n-1-S
, S2n-1-S 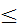 S2n-1-S
S2n-1-S  =
= 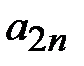 , тоесть
, тоесть 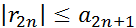 . Таким образом, во всех случаях остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине.
. Таким образом, во всех случаях остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине.
Признак Дирихле-Абеля
Теорема (Признак Дирихле-Абеля): Пусть числовой ряд имеет вид  nbn. Если {an} монотонная и
nbn. Если {an} монотонная и 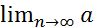 n=0,а последовательность частичных сумм {Bn}, Bn=
n=0,а последовательность частичных сумм {Bn}, Bn=  n – ограничена, то ряд сходится.
n – ограничена, то ряд сходится.
Следствие.
Признак Лейбница следует из признака Дирихле: {an} монотонна и 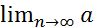 n=0, a|
n=0, a| 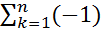 k-1|≤1.
k-1|≤1.
Пример. 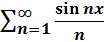 , x≠2
, x≠2 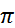 k.
k.
an=  - монотонно убывающая,
- монотонно убывающая, 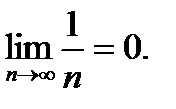
Bn= 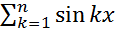 =
= 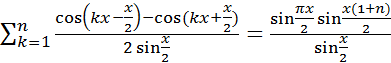 ; |Bn|≤
; |Bn|≤  и ряд сходится по признаку Дирихле.
и ряд сходится по признаку Дирихле.
Непрерывность суммы РСФР
Теорема (Непрерывность суммы равномерно сходящихся ФР): Пусть члены  ФР
ФР 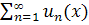 непрерывны на [a,b], ряд равномерно сходится к S(x) на [a,b]. Тогда сумма ряда S(x) непрерывна на [a,b].
непрерывны на [a,b], ряд равномерно сходится к S(x) на [a,b]. Тогда сумма ряда S(x) непрерывна на [a,b].
( Докажем  [a,b]
[a,b]  S(x0), т.е.
S(x0), т.е.
 >0
>0  >0:
>0:  .
.
Рассмотрим 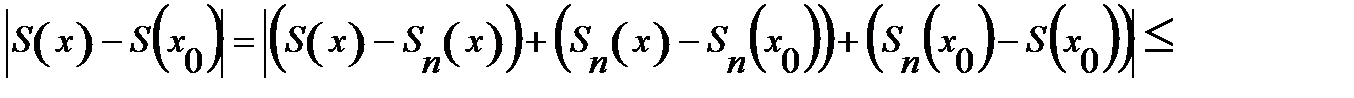
 (*).
(*).
Так как:
а) ФР 
 >0
>0  ,
,  [a,b]
[a,b]  (в том числе для
(в том числе для  );
);
в)  =u1(x)+...+un(x)- непрерывна на[a,b]
=u1(x)+...+un(x)- непрерывна на[a,b]
 >0
>0  >0:
>0:  [a,b]:
[a,b]:  <
<  , то в силу (*) при
, то в силу (*) при  выполняется
выполняется  .)
.)
Замечание. 
 =
=  =
= 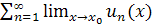
Замечание. Условия теоремы носят достаточный, но не обходимый характер (т.е. есть ряды составленные из непрерывных функций сходятся неравномерно, но имеют непрерывную сумму)
Основные элементарные ФКП
1) линейная w=az+b – непрерывна на z
2) степенная w=zn
3) дробнолинейная 

 0
0
4) w=ez=ex(cosy+isiny)
5) логорифмическая w=Lnz=ln|z|+iargz+2nki
6) тригонометрические 

7) обратные тригонометрические cosiz=chsiniz=ish
+ 21.Дифференцирование ФКП. Условия Коши-Римана.
Пусть 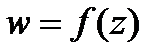 определена и одназн. в
определена и одназн. в  .Если
.Если 
 ,то ф-я дифф-ма в
,то ф-я дифф-ма в  .
.
Т.е. 

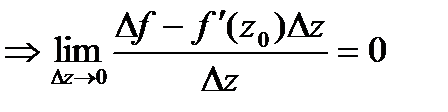 .
.  (*).
(*).
Если ф-я диф-ма в  ,то её приращение представимо в виде (*). Пусть представимо так:
,то её приращение представимо в виде (*). Пусть представимо так:  (**),
(**),  не зависит от
не зависит от  . Тогда
. Тогда  Чтобы
Чтобы  была диф-ма в
была диф-ма в  чтобы её приращ. в
чтобы её приращ. в  было в виде (*).
было в виде (*).
Если  -диф-мы в
-диф-мы в  1)
1) 
2)  3)
3)  4)
4)  -диф-ма.в
-диф-ма.в 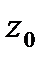
 Если
Если 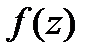 -диф. в
-диф. в 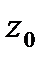 ,то
,то  -непрерывна в
-непрерывна в 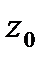 .
.
□по св-ву 1:  непрер. ■ Если
непрер. ■ Если  -диф. в
-диф. в 
 -диф-мы в
-диф-мы в  . Обратное не всегда верно.
. Обратное не всегда верно.
+21Теорема Коши-Римана. Пусть  -определена и однозн.в
-определена и однозн.в  .Чтобы
.Чтобы 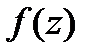 была диф-ма в
была диф-ма в  были диф-мы в
были диф-мы в 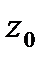 и выполнялись:
и выполнялись:  в
в 
 .
.
□ Необ. Пусть  .
.
а)  .
. 

 .
.
б)  .
. 

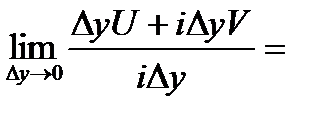
 .
. 
 (***).
(***).
Дост.  -диф-мы в
-диф-мы в  и выполняется (***).
и выполняется (***). 


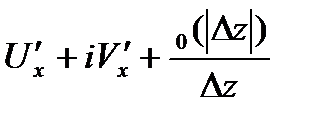 при
при  . Т.е.
. Т.е. 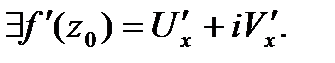 ■
■
Теорема Морера.
Пусть 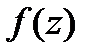 -непрерывная в односв.области
-непрерывная в односв.области 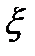 и
и 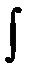 от
от 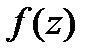
 замкнутому контуру, целиком
замкнутому контуру, целиком 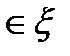 ,равен 0. Тогда
,равен 0. Тогда  -аналитическая в обл-ти
-аналитическая в обл-ти 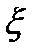 .
.
□При условиях теоремы 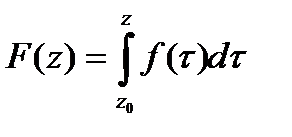 ,где
,где 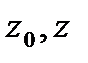 -произвольные
-произвольные  области
области 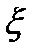 , а
, а 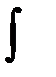 берётся по
берётся по  пути, соединяющему эти
пути, соединяющему эти  в обл-ти
в обл-ти 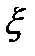 ,является аналитической в этой обл-ти ф-ей, причём
,является аналитической в этой обл-ти ф-ей, причём 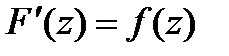 . Но, как было только что установлено, производная аналитической ф-ии также является анал.ф-ей, т.е.
. Но, как было только что установлено, производная аналитической ф-ии также является анал.ф-ей, т.е. 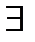 нерерывная производная ф-ии
нерерывная производная ф-ии 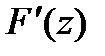 , а именно ф-ия
, а именно ф-ия 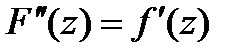 ,что и доказывает теорему.■
,что и доказывает теорему.■
Эта теорема в определённом смысле явл. обратной по отношении к т.Коши. Её легко обобщить на многосвязные области.
Принцип максимума модуля.
Пусть 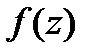 -анал-ая в обл.
-анал-ая в обл. 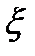 и непрерыв. в замкн. обл.
и непрерыв. в замкн. обл. 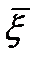 .Тогда или
.Тогда или 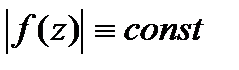 или максимальные знач-я
или максимальные знач-я 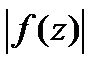 достигаются только на границе области.
достигаются только на границе области.
□ 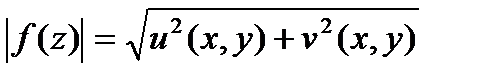 по условию непрерывная в замкн.области.Она достигает своего макс.значения
по условию непрерывная в замкн.области.Она достигает своего макс.значения 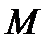 в какой-то
в какой-то 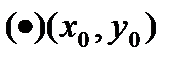 данной обл-ти.Т.е.
данной обл-ти.Т.е. 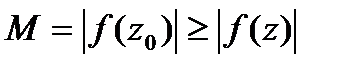 ,
, 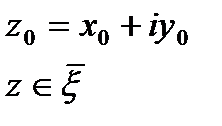 (*). Пусть
(*). Пусть 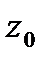 -внутр.точкаобл-ти
-внутр.точкаобл-ти 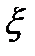 . Построим в
. Построим в 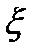 круг
круг 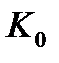 радиуса
радиуса 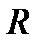 с центром в
с центром в 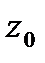 .Пишем ф-лу среднего для
.Пишем ф-лу среднего для 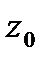 и
и 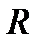 учитвая (*):
учитвая (*): 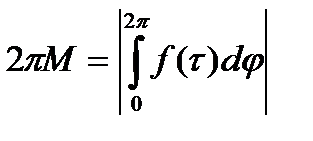

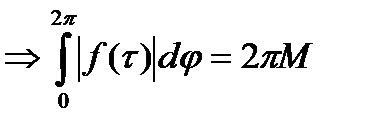 (**).
(**).
Т.к. 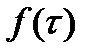 непрерывна на контуре интегрирования и из (*)
непрерывна на контуре интегрирования и из (*) 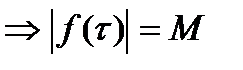 при
при 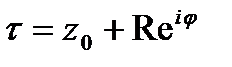 (***). По (*)
(***). По (*) 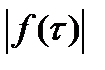 не может быть
не может быть 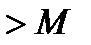 . Если предположим, что в какой-то
. Если предположим, что в какой-то 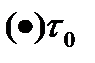 интегрирования модуль
интегрирования модуль 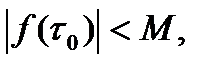 то из непрерыв.
то из непрерыв. 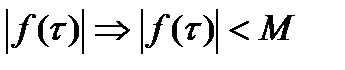 и в некой
и в некой 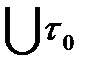 , т.е. можно указать отрезок инт-ия
, т.е. можно указать отрезок инт-ия 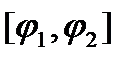 , на котором
, на котором 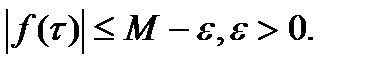 Тогда
Тогда 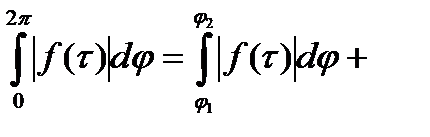
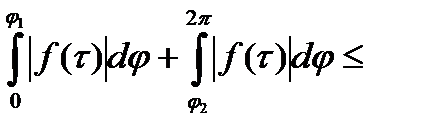
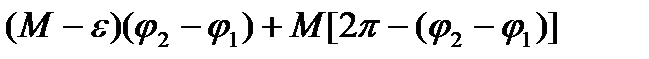
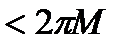 ,что противоречит (**).Значит (***) имеет место.■
,что противоречит (**).Значит (***) имеет место.■
Теорема Лиувилля.
Пусть на всей компл.пл-ти ф-ия 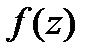 аналитическая, а
аналитическая, а 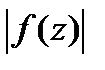 равномерно ограничен. Тогда
равномерно ограничен. Тогда 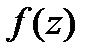 тождественно = постоянной. □Пишем
тождественно = постоянной. □Пишем 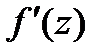 в
в 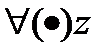 :
: 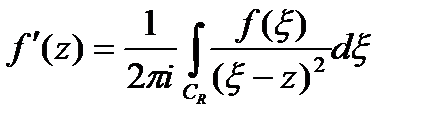 ,интегрирование будем вести по окружности
,интегрирование будем вести по окружности 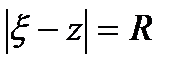 . Из условия
. Из условия 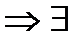 такая
такая 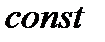
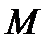 ,что
,что 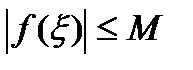 независимо от
независимо от 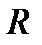 . Поэтому
. Поэтому 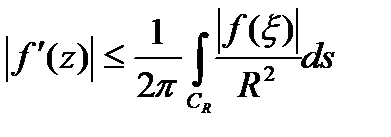
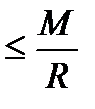 . Т.к.
. Т.к. 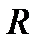 можно выбрать сколь угодно большим, а
можно выбрать сколь угодно большим, а 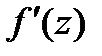 не зависит от
не зависит от 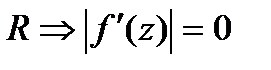 . Т.к. выбираем
. Т.к. выбираем 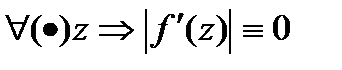 на всей компл.пл-ти.
на всей компл.пл-ти. 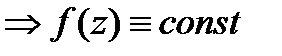 . ■
. ■
Основная теорема алгебры
Полином 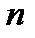 -ой степени имеет на компл.пл-ти ровно
-ой степени имеет на компл.пл-ти ровно 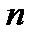 нулей (с учётом их кратности).
нулей (с учётом их кратности).
□Представим полином 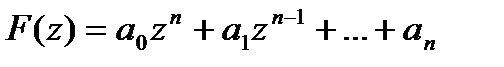 в виде
в виде 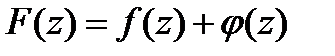 , где
, где 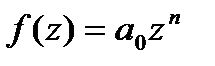 ,
, 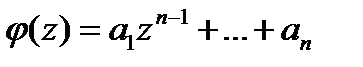 . Составим
. Составим 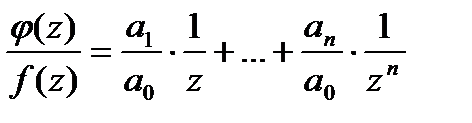 . При
. При  заданных значениях
заданных значениях 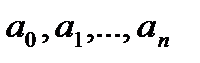 всегда найдётся такое знач.
всегда найдётся такое знач. 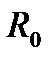 , что для всех знач.
, что для всех знач. 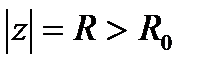 имеет место:
имеет место: 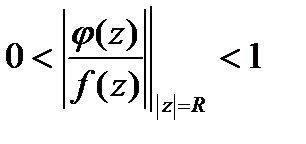 . По теор.Руше
. По теор.Руше 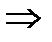 , что полное число нулей ф-ии
, что полное число нулей ф-ии 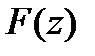 в
в 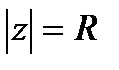 равно числу нулей в этом круге ф-ии
равно числу нулей в этом круге ф-ии 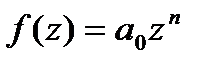 . Но
. Но 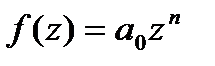 на всей компл.пл-ти имеет!
на всей компл.пл-ти имеет! 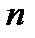 -кратный нуль -
-кратный нуль - 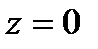 .Отсюда в силу произвольности
.Отсюда в силу произвольности 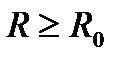 и следует утверждение теоремы.■
и следует утверждение теоремы.■
Я теорема Вейерштрасса.
Пусть ф-ии 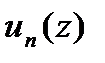 -аналит-ие в обл.
-аналит-ие в обл.  ,непрерывные в
,непрерывные в 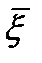 и ряд
и ряд
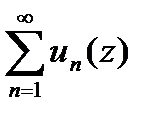 сход.равномерно на границе
сход.равномерно на границе 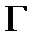 этой обл-ти.Тогда ряд
этой обл-ти.Тогда ряд 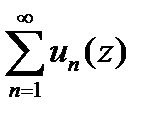 равном.сход. и в
равном.сход. и в 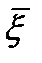 .
.
□Разность частичных сумм данного ряда, ф-я 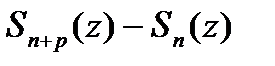 ,как конечная сумма аналит-их ф-ий, явл.аналитической в
,как конечная сумма аналит-их ф-ий, явл.аналитической в  и непрер.в
и непрер.в 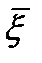 .Из равном.сход.
.Из равном.сход. 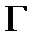
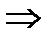

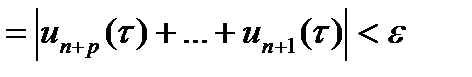 ,при
,при 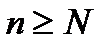 для
для  натурального
натурального 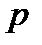 и всех
и всех 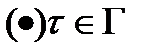 одновременно.
одновременно.
По теор.о максимуме аналит-ой ф-ии  при
при 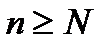 для
для  натурального
натурального 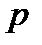 и для всех
и для всех 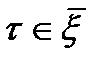 . Выполнен кр.Коши, что и доказывает теорему.■
. Выполнен кр.Коши, что и доказывает теорему.■
Теорема Абеля.
Если степенной ряд 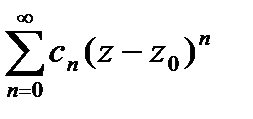 сход. в некот.
сход. в некот. 
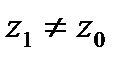 ,то он абсолютно сходится в
,то он абсолютно сходится в 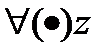 ,удовлетворяющую
,удовлетворяющую 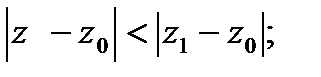 причём в
причём в 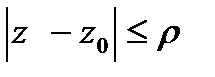 радиуса
радиуса 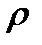
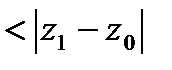 , ряд сходится равномерно.
, ряд сходится равномерно.
□Обозначим 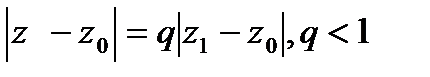 . Т.к.
. Т.к. 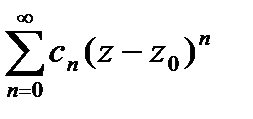 должен сходится, то при
должен сходится, то при 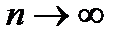 его члены
его члены 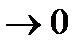
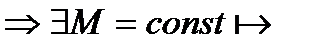
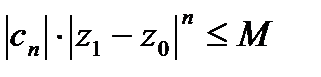 .
. 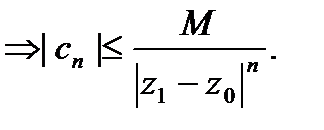
Тогда 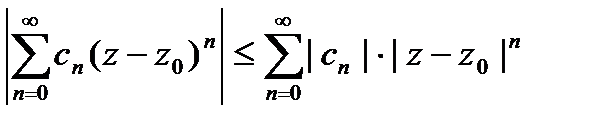
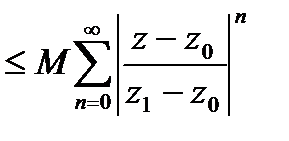 (*).
(*).
По условию 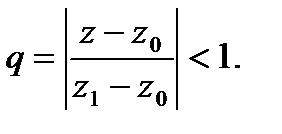
 сходится. Из (*)
сходится. Из (*) 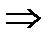 сходимость рассматриваемого ряда. Чтобы доказать равномерную сход-ть
сходимость рассматриваемого ряда. Чтобы доказать равномерную сход-ть 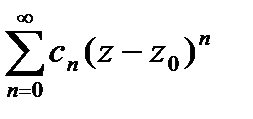 в круге
в круге 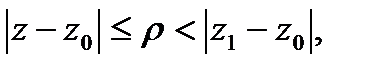 достаточно, по приз. Вайерштр., построить сходящийся числовой ряд, мажорирующий данный ряд в рассматриваемой области. Такой ряд – это
достаточно, по приз. Вайерштр., построить сходящийся числовой ряд, мажорирующий данный ряд в рассматриваемой области. Такой ряд – это 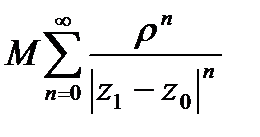 , тоже представляюет сумму бескон.геом. прогрессии со знаменателем
, тоже представляюет сумму бескон.геом. прогрессии со знаменателем 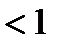 ■
■
Теорема Тейлора.
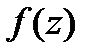 , аналитическая внутри
, аналитическая внутри 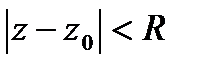 , может быть представлена в этом круге степ.рядом
, может быть представлена в этом круге степ.рядом 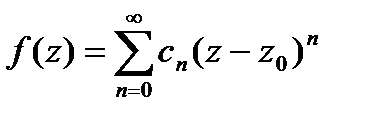 , причём он определён однозначно.
, причём он определён однозначно.
□Выберем 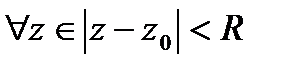 , построим окружность
, построим окружность 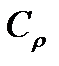 с центром в
с центром в 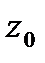 радиуса
радиуса 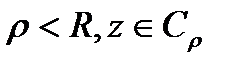 . Имеем
. Имеем 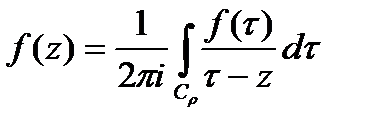 (*). Преобразуем:
(*). Преобразуем: 
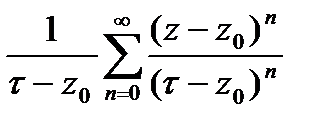 (**).
(**).
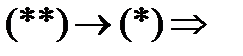
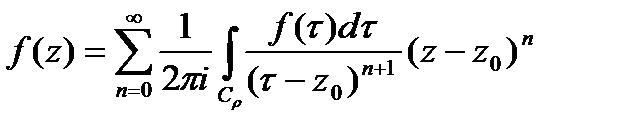

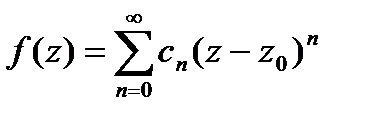 .
. 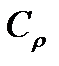 по теор. Коши можно заменить на
по теор. Коши можно заменить на  замкн.контур
замкн.контур 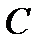 ,лежащим в
,лежащим в  .
.
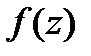 , аналитическая внутри
, аналитическая внутри 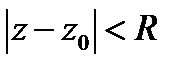 , разлаг.в нём в сходящийся степ. ряд. Коэф-ты разложения
, разлаг.в нём в сходящийся степ. ряд. Коэф-ты разложения 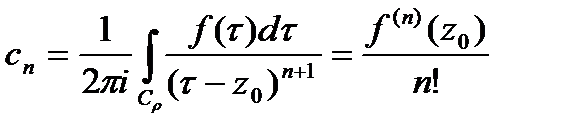 .
.
Докажем! разложения. Пусть есть другое: 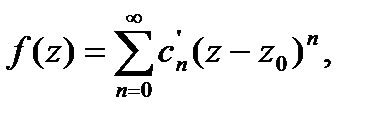 где хотя бы один
где хотя бы один 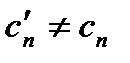 . Ряд сход-ся в
. Ряд сход-ся в 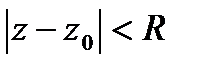 . Из всего
. Из всего  .?!?
.?!?  ! доказана. ■
! доказана. ■
Теорема Лорана.
(1) 
Ряд Лорана сход-ся, если сход-ся правильная и главная части. 
Теорема. Если ряд Лорана сх-ся, то он сх-ся в некотором кольце.
f(z)= 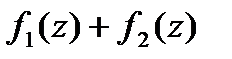
Теорема Лорана. Если f(z)-аналит. в r<  ,
,
то f(z)= 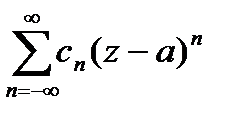
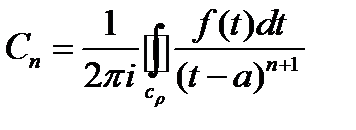 ,
, 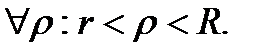
Неравенство Коши.
f(z) огран. в 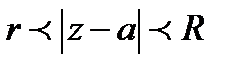 :
: 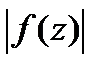
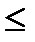 M
M
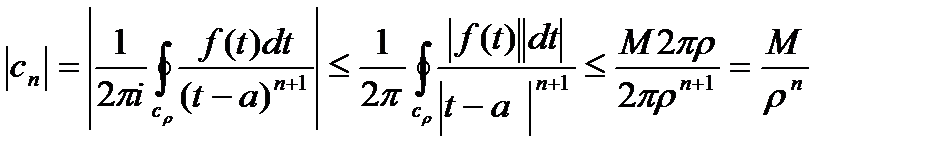
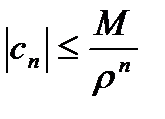 -неравенство Коши
-неравенство Коши
Теорема Сохоцкого.
Если a -с.о.т., то для любого комплексного числа a, в том числе и для 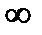 , найдётся
, найдётся 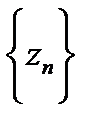

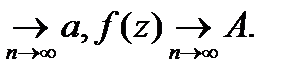
Теорема единственности.
F(z) и g(z) – аналитичны в некоторой области D и их значения совпадают на некоторой последовательности точек
F(zn)=g(zn) zn 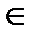 Dzn
Dzn 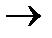 a
a  D при n
D при n 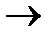
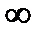
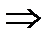 f(z)
f(z)  g(z) во всей области D
g(z) во всей области D
□ Берем 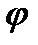 (z)=f(z)-g(z)
(z)=f(z)-g(z) 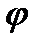 (zn)=f(zn)-g(zn)=0 zn – нули функций по условию
(zn)=f(zn)-g(zn)=0 zn – нули функций по условию
zn 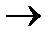 a при n
a при n 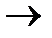
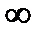 и по теореме о нулях функции
и по теореме о нулях функции 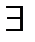 U(a) такая что
U(a) такая что 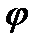 (z)=0
(z)=0
для z1 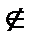 D
D 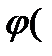 z1)=0
z1)=0  окружности t1 бесконечно много нулей
окружности t1 бесконечно много нулей 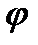 (z)
(z)  t1-предельнаяточка множества
t1-предельнаяточка множества 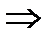
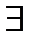 U(t1) такой что
U(t1) такой что 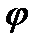 (z)
(z)  0 и так далее
0 и так далее
z1 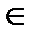 U(tk)
U(tk) 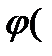 z1)=0
z1)=0 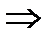
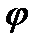 (z)
(z)  0 в области D ■
0 в области D ■
Свойства сходящихся числовых рядов
1°. Пусть ряд 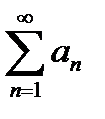 сходится и
сходится и 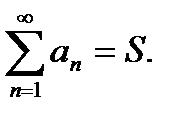 Тогда для любого
Тогда для любого 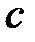 (
(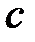 = const) сходится ряд
= const) сходится ряд 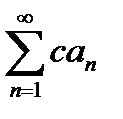 и имеет сумму
и имеет сумму 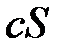 .{Пусть
.{Пусть 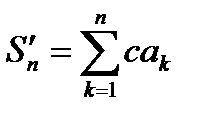 .
. 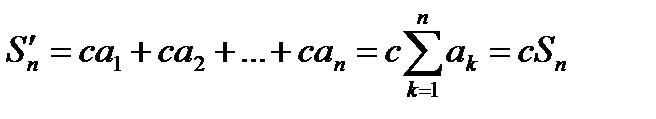 ,
, 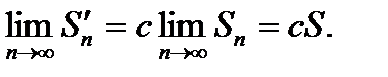 }.
}.
2°. Если сходятся ряды 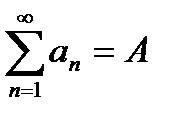 и
и 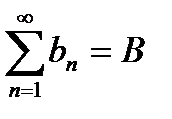 , то сходится ряд
, то сходится ряд 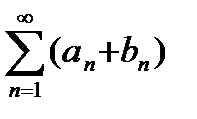 и имеет сумму A+B.
и имеет сумму A+B.
{Пусть 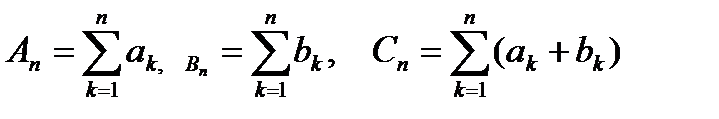 . =>
. => 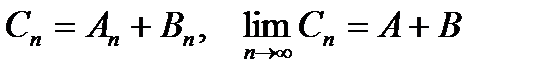 }.
}.
3°. Если 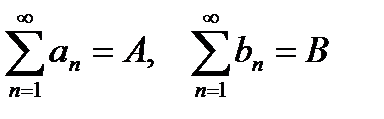 , то для любых чисел
, то для любых чисел  и
и 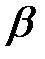
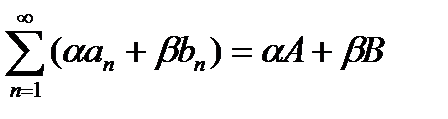 . {Следует из 1° и 2°}
. {Следует из 1° и 2°}
4°. Если сходится ряд 
|
|
|



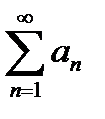 сходится и
сходится и 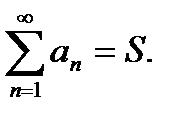 Тогда для любого
Тогда для любого 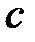 (
(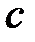 = const) сходится ряд
= const) сходится ряд 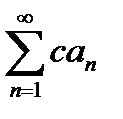 и имеет сумму
и имеет сумму 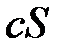 .{Пусть
.{Пусть 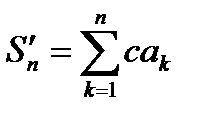 .
. 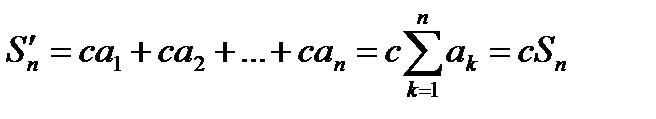 ,
, 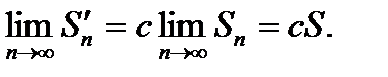 }.
}.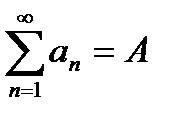 и
и 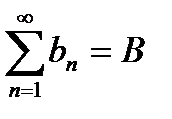 , то сходится ряд
, то сходится ряд 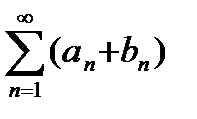 и имеет сумму A+B.
и имеет сумму A+B.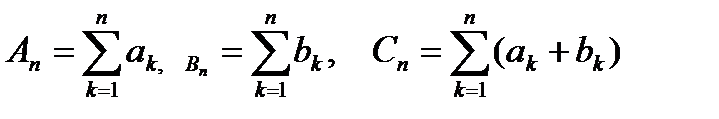 . =>
. => 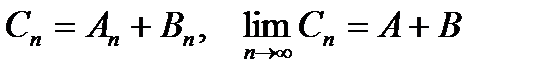 }.
}.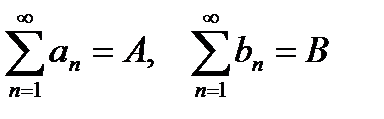 , то для любых чисел
, то для любых чисел  и
и 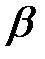
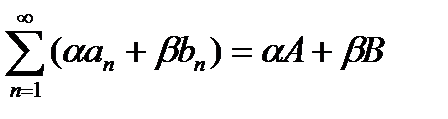 . {Следует из 1° и 2°}
. {Следует из 1° и 2°}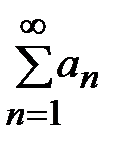 , то сходится и любой его остаток. Если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
, то сходится и любой его остаток. Если сходится какой-нибудь остаток ряда, то сходится и сам ряд. , его p-ую частичную сумму
, его p-ую частичную сумму 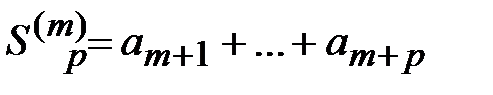 . Пусть
. Пусть 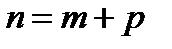 .
. 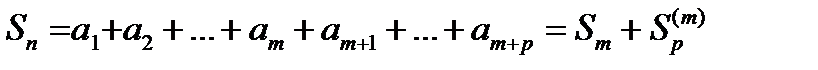 ;
; 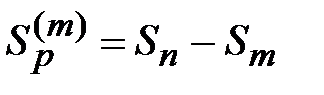 (*) Зафиксируем
(*) Зафиксируем 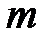 , а
, а 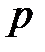 устремим к бесконечности. Тогда
устремим к бесконечности. Тогда 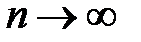 .
. 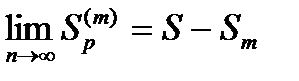 и остаток ряда
и остаток ряда 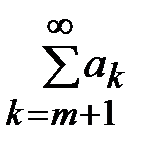 сходится.
сходится. , то из (*) следует:
, то из (*) следует: 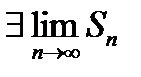 и ряд
и ряд 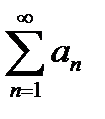 сходится.
сходится.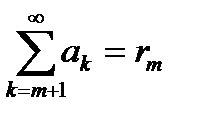 . Тогда из (*) следует:
. Тогда из (*) следует:  (**) или
(**) или 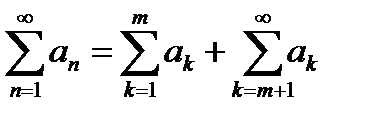 .} Выводы: 1. Переходя в (**) к пределу при
.} Выводы: 1. Переходя в (**) к пределу при 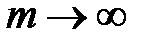 , получаем
, получаем 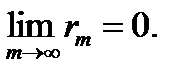 2.Отбрасывание конечного числа начальных членов ряда или присоединение в начале его нескольких новых членов не отражается на поведении ряда (в смысле его сходимости или расходимости).
2.Отбрасывание конечного числа начальных членов ряда или присоединение в начале его нескольких новых членов не отражается на поведении ряда (в смысле его сходимости или расходимости).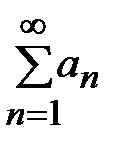 сходился, необходимо и достаточно, чтобы
сходился, необходимо и достаточно, чтобы  и
и 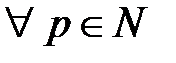 выполнялось бы:
выполнялось бы:  .{Сходимость числового ряда определяется сходимостью числовой последовательности {
.{Сходимость числового ряда определяется сходимостью числовой последовательности {  }. Ранее доказано: для того чтобы последовательность {
}. Ранее доказано: для того чтобы последовательность {  и
и  выполнялось бы:
выполнялось бы: 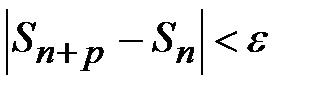 или
или  .}
.} . Переходя к пределу при
. Переходя к пределу при 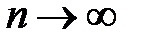 , получим:
, получим:  . Тот же результат можно получить из критерия Коши, полагая p = 1. Очевидно, условие
. Тот же результат можно получить из критерия Коши, полагая p = 1. Очевидно, условие  является необходимым, но не достаточным условием сходимости числового ряда. (НО: Ряд
является необходимым, но не достаточным условием сходимости числового ряда. (НО: Ряд  расходится, однако
расходится, однако  )
) (1) и
(1) и  (2). Если, начиная с некоторого номера выполняется:
(2). Если, начиная с некоторого номера выполняется:  (3),
(3),  , то из сходимости ряда (2)
, то из сходимости ряда (2)  сходимость ряда (1); из расходимости ряда (1)
сходимость ряда (1); из расходимости ряда (1)  расходимость ряда (2).
расходимость ряда (2). выполняется для всех n. Пусть
выполняется для всех n. Пусть  . Очевидно, последовательности {
. Очевидно, последовательности { 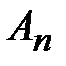 } и {
} и { 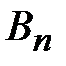 } – монотонные неубывающие. Пусть ряд (2) сходится. Тогда {
} – монотонные неубывающие. Пусть ряд (2) сходится. Тогда {  } ограничена:
} ограничена:  . Но тогда, в силу (3),
. Но тогда, в силу (3),  и ряд (1) – также сходится.
и ряд (1) – также сходится. Если существует
Если существует  то ряды (1) и (2) сходятся либо расходятся одновременно. { Пусть ряд (2) сходится.Из существования
то ряды (1) и (2) сходятся либо расходятся одновременно. { Пусть ряд (2) сходится.Из существования  :
:  , откуда получаем:
, откуда получаем:  или
или  следует сходимость ряда (1). Пусть ряд (2) расходится.Существует
следует сходимость ряда (1). Пусть ряд (2) расходится.Существует  , откуда аналогичным образом получаем:
, откуда аналогичным образом получаем: 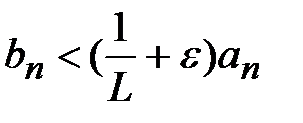 . Если бы сходился ряд (1), а вместе с ним и ряд
. Если бы сходился ряд (1), а вместе с ним и ряд  , то по теореме 1 сходился бы и ряд (2). А это не так. Значит, ряд (1) также расходится.}
, то по теореме 1 сходился бы и ряд (2). А это не так. Значит, ряд (1) также расходится.} . Так как
. Так как  , а ряд
, а ряд  - расходится (
- расходится ( то расходится и ряд
то расходится и ряд  .
. , то при
, то при  ряд (1) сходится; при
ряд (1) сходится; при  расходится, при
расходится, при  этот признак не даёт возможности судить о поведении ряда.
этот признак не даёт возможности судить о поведении ряда.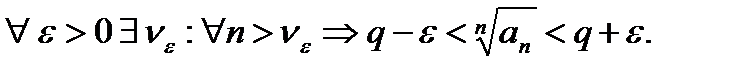
 начиная с некоторого номера
начиная с некоторого номера  <
<  1. Ряд сходится.
1. Ряд сходится.
 начиная с некоторого номера
начиная с некоторого номера  >1. Ряд расходится. }
>1. Ряд расходится. } Если, начиная с некоторого номера
Если, начиная с некоторого номера 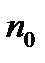 ,
,  для всех
для всех  , то ряд (1) сходится. Если же
, то ряд (1) сходится. Если же  , то ряд (1) расходится. { Пусть
, то ряд (1) расходится. { Пусть  . Для
. Для 
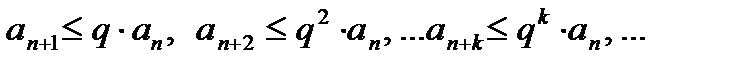 Т.к. ряд
Т.к. ряд  - сходится, то, по признаку сравнения, сходится и остаток ряда
- сходится, то, по признаку сравнения, сходится и остаток ряда  , а значит, сходится ряд
, а значит, сходится ряд  (1). Пусть для
(1). Пусть для 
 . Т.е.
. Т.е. 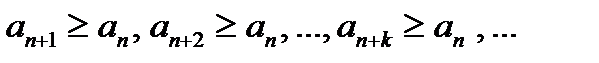 и
и  , не выполняется необходимое условие сходимости ряда. Ряд расходится. }
, не выполняется необходимое условие сходимости ряда. Ряд расходится. }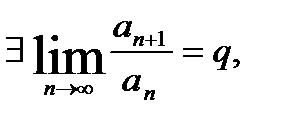 то при
то при  ряд (1) сходится, при
ряд (1) сходится, при  расходится, при
расходится, при  этот признак не даёт возможности судить о поведении ряда.
этот признак не даёт возможности судить о поведении ряда. a)
a)  начиная с некоторого номера
начиная с некоторого номера  Ряд сх.
Ряд сх.
 начиная с некоторого номера
начиная с некоторого номера  >1. Ряд расх. }
>1. Ряд расх. }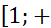 ∞). Тогда ряд
∞). Тогда ряд  , где
, где  сходится тогда и только тогда, когда сходится несобственный интеграл
сходится тогда и только тогда, когда сходится несобственный интеграл  (2)
(2) ], поэтому имеет смысл
], поэтому имеет смысл  . Так как f(x)-убывает на
. Так как f(x)-убывает на  f(k+1)
f(k+1)  . Проинтегрируем последнее неравенство по отрезку
. Проинтегрируем последнее неравенство по отрезку  :
:  , k=1,2,3.4...
, k=1,2,3.4... Обозначим,
Обозначим,  Тогда
Тогда
 монотонна (
монотонна ( ) и ограничена. Тогда ограничена и последовательность
) и ограничена. Тогда ограничена и последовательность  . А поскольку она монотонно возрастает, то является сходящейся.
. А поскольку она монотонно возрастает, то является сходящейся. – монотонная, сходящаяся последовательность, следовательно, ограничена.
– монотонная, сходящаяся последовательность, следовательно, ограничена. ; интеграл (2) сходится.}
; интеграл (2) сходится.} , s>0, Рассмотрим f(x)=
, s>0, Рассмотрим f(x)=  на [1,
на [1, 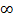 );
);

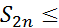 S
S 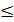 S2n-1
S2n-1 , S2n-1-S
, S2n-1-S 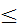 S2n-1-S
S2n-1-S  =
= 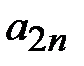 , тоесть
, тоесть 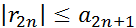 . Таким образом, во всех случаях остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине.
. Таким образом, во всех случаях остаток ряда Лейбница имеет знак своего первого члена и меньше его по абсолютной величине. nbn. Если {an} монотонная и
nbn. Если {an} монотонная и 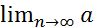 n=0,а последовательность частичных сумм {Bn}, Bn=
n=0,а последовательность частичных сумм {Bn}, Bn=  n – ограничена, то ряд сходится.
n – ограничена, то ряд сходится.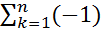 k-1|≤1.
k-1|≤1.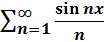 , x≠2
, x≠2 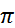 k.
k. - монотонно убывающая,
- монотонно убывающая, 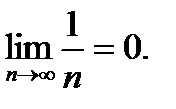
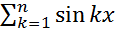 =
= 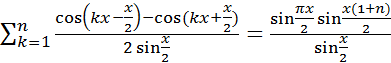 ; |Bn|≤
; |Bn|≤  и ряд сходится по признаку Дирихле.
и ряд сходится по признаку Дирихле. ФР
ФР 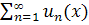 непрерывны на [a,b], ряд равномерно сходится к S(x) на [a,b]. Тогда сумма ряда S(x) непрерывна на [a,b].
непрерывны на [a,b], ряд равномерно сходится к S(x) на [a,b]. Тогда сумма ряда S(x) непрерывна на [a,b]. [a,b]
[a,b]  S(x0), т.е.
S(x0), т.е. >0
>0  >0:
>0:  .
.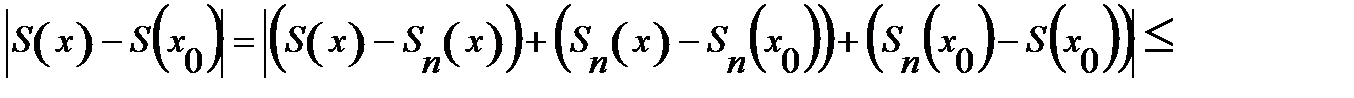
 (*).
(*).
 >0
>0  ,
,  [a,b]
[a,b]  (в том числе для
(в том числе для  );
); =u1(x)+...+un(x)- непрерывна на[a,b]
=u1(x)+...+un(x)- непрерывна на[a,b] <
<  , то в силу (*) при
, то в силу (*) при  выполняется
выполняется  .)
.)
 =
=  =
= 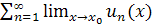


 0
0

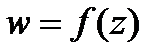 определена и одназн. в
определена и одназн. в  .Если
.Если 
 ,то ф-я дифф-ма в
,то ф-я дифф-ма в  .
.

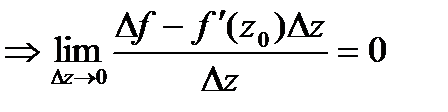 .
.  (*).
(*). ,то её приращение представимо в виде (*). Пусть представимо так:
,то её приращение представимо в виде (*). Пусть представимо так:  (**),
(**),  не зависит от
не зависит от  . Тогда
. Тогда  Чтобы
Чтобы  была диф-ма в
была диф-ма в  чтобы её приращ. в
чтобы её приращ. в  было в виде (*).
было в виде (*). -диф-мы в
-диф-мы в  1)
1) 
 3)
3)  4)
4)  -диф-ма.в
-диф-ма.в 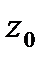
 Если
Если 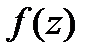 -диф. в
-диф. в  -непрерывна в
-непрерывна в  непрер. ■ Если
непрер. ■ Если  -диф. в
-диф. в 
 -диф-мы в
-диф-мы в  . Обратное не всегда верно.
. Обратное не всегда верно. -определена и однозн.в
-определена и однозн.в 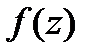 была диф-ма в
была диф-ма в  были диф-мы в
были диф-мы в 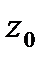 и выполнялись:
и выполнялись:  в
в 
 .
. .
. .
. 

 .
. .
. 

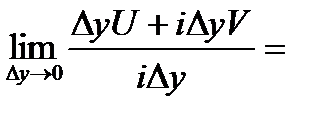
 .
. 
 (***).
(***). -диф-мы в
-диф-мы в  и выполняется (***).
и выполняется (***). 


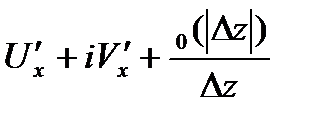 при
при  . Т.е.
. Т.е. 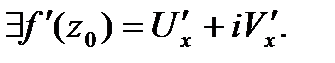 ■
■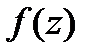 -непрерывная в односв.области
-непрерывная в односв.области 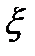 и
и 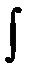 от
от 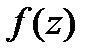
 замкнутому контуру, целиком
замкнутому контуру, целиком 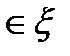 ,равен 0. Тогда
,равен 0. Тогда  -аналитическая в обл-ти
-аналитическая в обл-ти 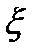 .
.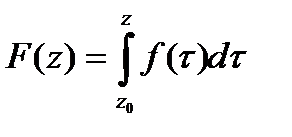 ,где
,где 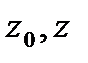 -произвольные
-произвольные  области
области 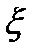 , а
, а 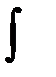 берётся по
берётся по  пути, соединяющему эти
пути, соединяющему эти 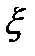 ,является аналитической в этой обл-ти ф-ей, причём
,является аналитической в этой обл-ти ф-ей, причём 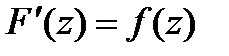 . Но, как было только что установлено, производная аналитической ф-ии также является анал.ф-ей, т.е.
. Но, как было только что установлено, производная аналитической ф-ии также является анал.ф-ей, т.е. 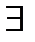 нерерывная производная ф-ии
нерерывная производная ф-ии 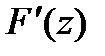 , а именно ф-ия
, а именно ф-ия 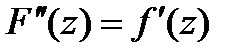 ,что и доказывает теорему.■
,что и доказывает теорему.■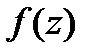 -анал-ая в обл.
-анал-ая в обл. 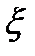 и непрерыв. в замкн. обл.
и непрерыв. в замкн. обл. 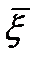 .Тогда или
.Тогда или 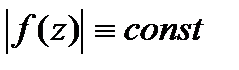 или максимальные знач-я
или максимальные знач-я 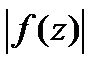 достигаются только на границе области.
достигаются только на границе области.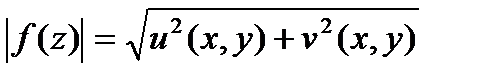 по условию непрерывная в замкн.области.Она достигает своего макс.значения
по условию непрерывная в замкн.области.Она достигает своего макс.значения 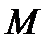 в какой-то
в какой-то 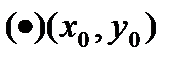 данной обл-ти.Т.е.
данной обл-ти.Т.е. 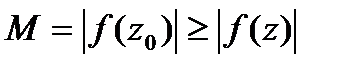 ,
, 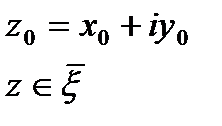 (*). Пусть
(*). Пусть 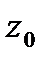 -внутр.точкаобл-ти
-внутр.точкаобл-ти 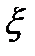 . Построим в
. Построим в 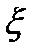 круг
круг 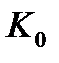 радиуса
радиуса 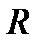 с центром в
с центром в 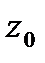 .Пишем ф-лу среднего для
.Пишем ф-лу среднего для 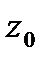 и
и 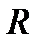 учитвая (*):
учитвая (*): 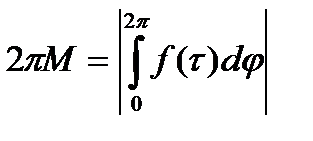

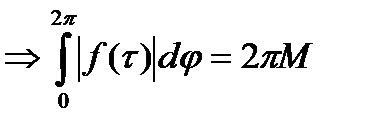 (**).
(**).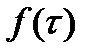 непрерывна на контуре интегрирования и из (*)
непрерывна на контуре интегрирования и из (*) 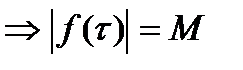 при
при 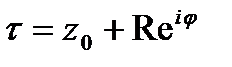 (***). По (*)
(***). По (*) 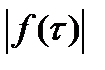 не может быть
не может быть 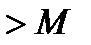 . Если предположим, что в какой-то
. Если предположим, что в какой-то 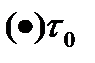 интегрирования модуль
интегрирования модуль 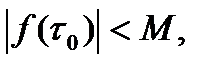 то из непрерыв.
то из непрерыв. 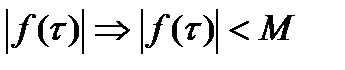 и в некой
и в некой 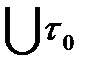 , т.е. можно указать отрезок инт-ия
, т.е. можно указать отрезок инт-ия 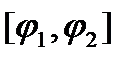 , на котором
, на котором 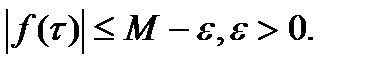 Тогда
Тогда 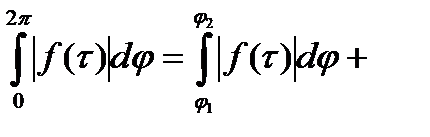
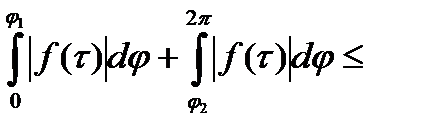
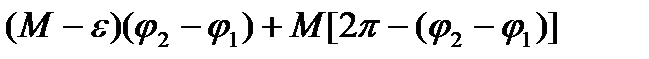
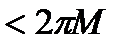 ,что противоречит (**).Значит (***) имеет место.■
,что противоречит (**).Значит (***) имеет место.■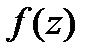 аналитическая, а
аналитическая, а 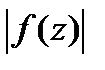 равномерно ограничен. Тогда
равномерно ограничен. Тогда 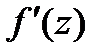 в
в 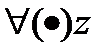 :
: 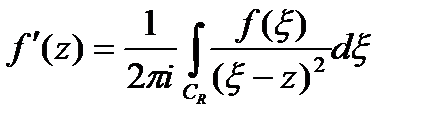 ,интегрирование будем вести по окружности
,интегрирование будем вести по окружности 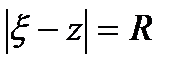 . Из условия
. Из условия 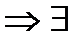 такая
такая 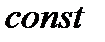
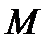 ,что
,что 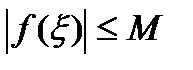 независимо от
независимо от 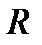 . Поэтому
. Поэтому 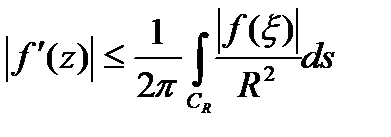
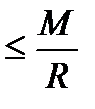 . Т.к.
. Т.к. 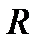 можно выбрать сколь угодно большим, а
можно выбрать сколь угодно большим, а 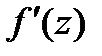 не зависит от
не зависит от 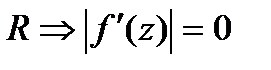 . Т.к. выбираем
. Т.к. выбираем 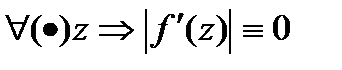 на всей компл.пл-ти.
на всей компл.пл-ти. 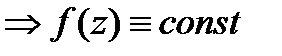 . ■
. ■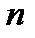 -ой степени имеет на компл.пл-ти ровно
-ой степени имеет на компл.пл-ти ровно 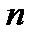 нулей (с учётом их кратности).
нулей (с учётом их кратности).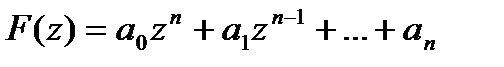 в виде
в виде 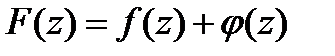 , где
, где 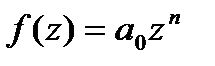 ,
, 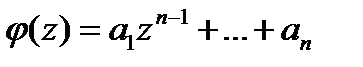 . Составим
. Составим 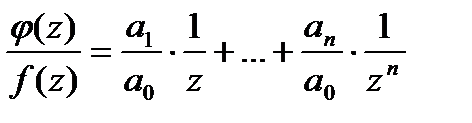 . При
. При  заданных значениях
заданных значениях 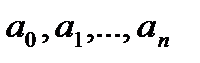 всегда найдётся такое знач.
всегда найдётся такое знач. 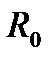 , что для всех знач.
, что для всех знач. 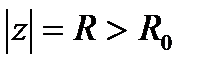 имеет место:
имеет место: 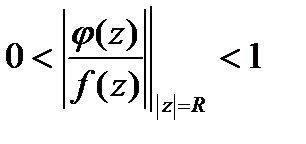 . По теор.Руше
. По теор.Руше 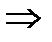 , что полное число нулей ф-ии
, что полное число нулей ф-ии 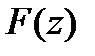 в
в 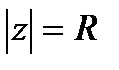 равно числу нулей в этом круге ф-ии
равно числу нулей в этом круге ф-ии 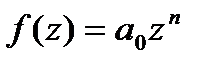 . Но
. Но 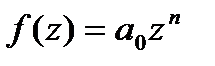 на всей компл.пл-ти имеет!
на всей компл.пл-ти имеет! 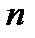 -кратный нуль -
-кратный нуль - 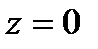 .Отсюда в силу произвольности
.Отсюда в силу произвольности 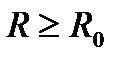 и следует утверждение теоремы.■
и следует утверждение теоремы.■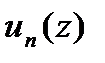 -аналит-ие в обл.
-аналит-ие в обл.  ,непрерывные в
,непрерывные в 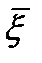 и ряд
и ряд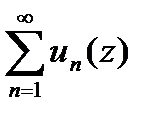 сход.равномерно на границе
сход.равномерно на границе 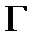 этой обл-ти.Тогда ряд
этой обл-ти.Тогда ряд 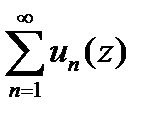 равном.сход. и в
равном.сход. и в 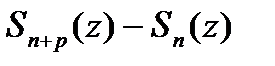 ,как конечная сумма аналит-их ф-ий, явл.аналитической в
,как конечная сумма аналит-их ф-ий, явл.аналитической в 

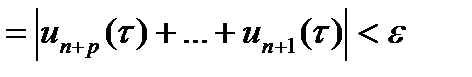 ,при
,при 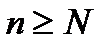 для
для  натурального
натурального 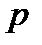 и всех
и всех 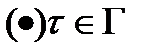 одновременно.
одновременно. при
при 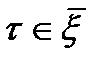 . Выполнен кр.Коши, что и доказывает теорему.■
. Выполнен кр.Коши, что и доказывает теорему.■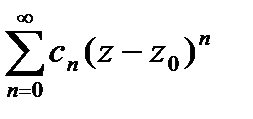 сход. в некот.
сход. в некот. 
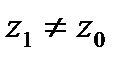 ,то он абсолютно сходится в
,то он абсолютно сходится в 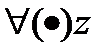 ,удовлетворяющую
,удовлетворяющую 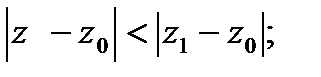 причём в
причём в 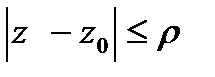 радиуса
радиуса 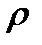
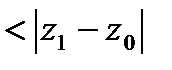 , ряд сходится равномерно.
, ряд сходится равномерно.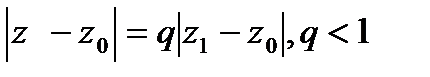 . Т.к.
. Т.к. 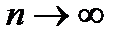 его члены
его члены 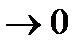
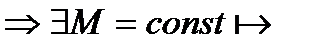
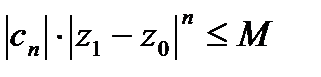 .
. 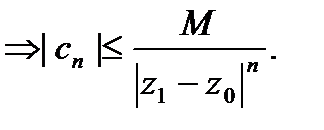
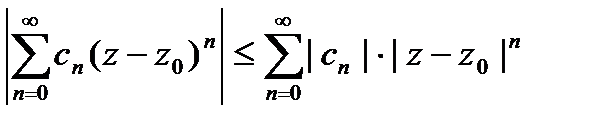
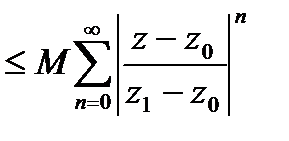 (*).
(*).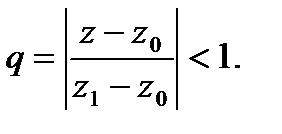
 сходится. Из (*)
сходится. Из (*) 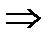 сходимость рассматриваемого ряда. Чтобы доказать равномерную сход-ть
сходимость рассматриваемого ряда. Чтобы доказать равномерную сход-ть 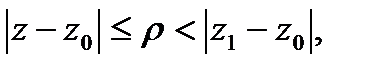 достаточно, по приз. Вайерштр., построить сходящийся числовой ряд, мажорирующий данный ряд в рассматриваемой области. Такой ряд – это
достаточно, по приз. Вайерштр., построить сходящийся числовой ряд, мажорирующий данный ряд в рассматриваемой области. Такой ряд – это 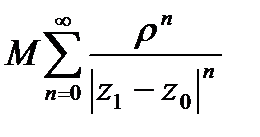 , тоже представляюет сумму бескон.геом. прогрессии со знаменателем
, тоже представляюет сумму бескон.геом. прогрессии со знаменателем 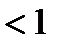 ■
■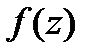 , аналитическая внутри
, аналитическая внутри 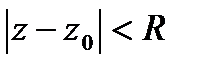 , может быть представлена в этом круге степ.рядом
, может быть представлена в этом круге степ.рядом 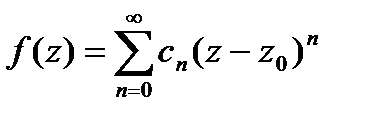 , причём он определён однозначно.
, причём он определён однозначно.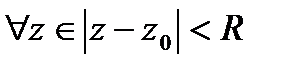 , построим окружность
, построим окружность 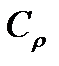 с центром в
с центром в 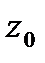 радиуса
радиуса 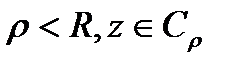 . Имеем
. Имеем 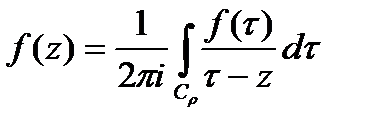 (*). Преобразуем:
(*). Преобразуем: 
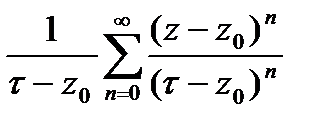 (**).
(**).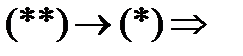
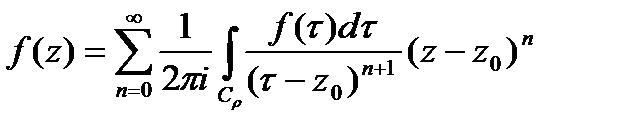

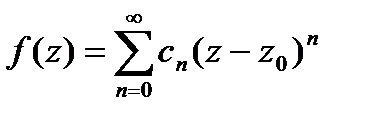 .
.  замкн.контур
замкн.контур 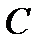 ,лежащим в
,лежащим в  .
.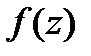 , аналитическая внутри
, аналитическая внутри 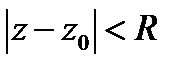 , разлаг.в нём в сходящийся степ. ряд. Коэф-ты разложения
, разлаг.в нём в сходящийся степ. ряд. Коэф-ты разложения 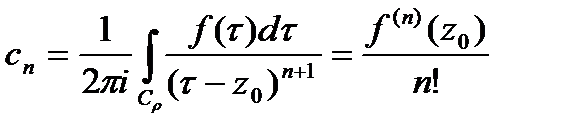 .
.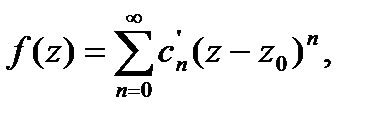 где хотя бы один
где хотя бы один 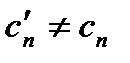 . Ряд сход-ся в
. Ряд сход-ся в 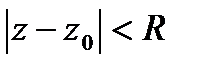 . Из всего
. Из всего  .?!?
.?!? 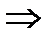 ! доказана. ■
! доказана. ■

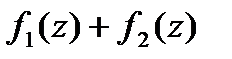
 ,
,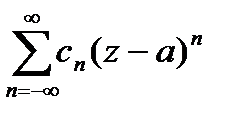
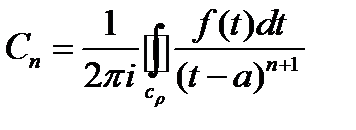 ,
, 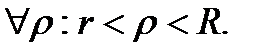
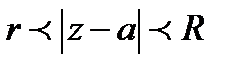 :
: 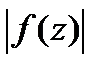
 M
M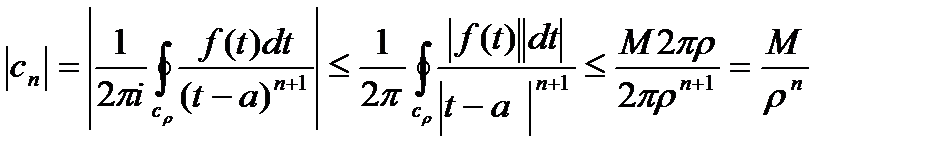
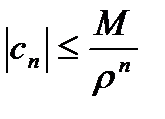 -неравенство Коши
-неравенство Коши , найдётся
, найдётся 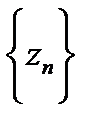
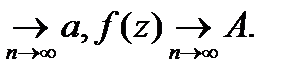
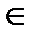 Dzn
Dzn 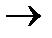 a
a  D при n
D при n 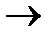
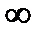
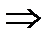 f(z)
f(z)  g(z) во всей области D
g(z) во всей области D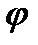 (z)=f(z)-g(z)
(z)=f(z)-g(z) 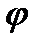 (zn)=f(zn)-g(zn)=0 zn – нули функций по условию
(zn)=f(zn)-g(zn)=0 zn – нули функций по условию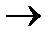 a при n
a при n 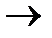
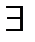 U(a) такая что
U(a) такая что 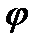 (z)=0
(z)=0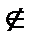 D
D 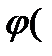 z1)=0
z1)=0  окружности t1 бесконечно много нулей
окружности t1 бесконечно много нулей 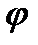 (z)
(z)  t1-предельнаяточка множества
t1-предельнаяточка множества 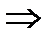
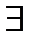 U(t1) такой что
U(t1) такой что  0 и так далее
0 и так далее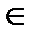 U(tk)
U(tk) 

