Рассмотрим на плоскости декартову прямоугольную систему координат  . Каждому комплексному числу
. Каждому комплексному числу  можно сопоставить точку с координатами
можно сопоставить точку с координатами 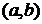 , и наоборот, каждой точке с координатами
, и наоборот, каждой точке с координатами 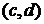 можно сопоставить комплексное число
можно сопоставить комплексное число  . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.
. Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.
Пример. Изобразим на комплексной плоскости числа  :
:

Рис. 9. Изображение комплексных чисел точками плоскости
Однако чаще комплексные числа изображают в виде вектора с началом в точке  , а именно, комплексное число
, а именно, комплексное число  изображается радиус-вектором точки с координатами
изображается радиус-вектором точки с координатами 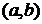 . В этом случае изображение комплексных чисел из предыдущего примера будет таким:
. В этом случае изображение комплексных чисел из предыдущего примера будет таким:

Рис. 10. Изображение комплексных чисел векторами
Отметим, что изображением суммы двух комплексных чисел  является вектор, равный сумме векторов, изображающих числа
является вектор, равный сумме векторов, изображающих числа 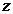 и
и  . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 11).
. Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 11).

Рис. 11. Изображение суммы комплексных чисел
Пусть комплексное число  изображается радиус-вектором. Тогда длина этого вектора называется модулем числа
изображается радиус-вектором. Тогда длина этого вектора называется модулем числа 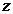 и обозначается
и обозначается  . Из рисунка 12 очевидно, что
. Из рисунка 12 очевидно, что 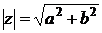 .
.

Рис. 12.Модуль и аргумент
Угол, образованный радиус-вектором числа 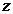 с осью
с осью  , называется аргументом числа
, называется аргументом числа 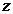 и обозначается
и обозначается  . Аргумент числа определяется не однозначно, а с точностью до числа, кратного
. Аргумент числа определяется не однозначно, а с точностью до числа, кратного  . Однако, обычно аргумент указывают в диапазоне от
. Однако, обычно аргумент указывают в диапазоне от  до
до 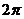 или в диапазоне от
или в диапазоне от  до
до  . Кроме того у числа
. Кроме того у числа  аргумент не определен.
аргумент не определен.
На рис. 9  равен углу
равен углу  . Из того же рисунка очевидно, что
. Из того же рисунка очевидно, что  .
.
С помощью этого соотношения можно находить аргумент комплексного числа:
 или
или  ,
,
причем первая формула действует, если изображение числа 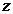 находится в первой или четвертой четверти, а вторая, если - во второй или третьей. Если
находится в первой или четвертой четверти, а вторая, если - во второй или третьей. Если  , то комплексное число изображается вектором на оси
, то комплексное число изображается вектором на оси  и его аргумент равен или.
и его аргумент равен или.
Тригонометрическая форма комплексного числа
Пусть  . Положим
. Положим  . Из рисунка 9 очевидно, что
. Из рисунка 9 очевидно, что  .
.
Тогда  . Это выражение запишем в виде
. Это выражение запишем в виде
 .
.
Последняя запись называется тригонометрической формой комплексного числа. В отличие от нее запись числа в виде  называют иногда алгебраической формой комплексного числа.
называют иногда алгебраической формой комплексного числа.
Пример. Запишите в тригонометрической форме числа  .
.
Решение. Находим модуль, аргумент, а затем выписываем тригонометрическую форму:






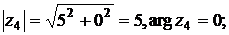
 .
.
Для возведения комплексного числа  в степень
в степень  , где
, где  - натуральное число применяется формула Муавра
- натуральное число применяется формула Муавра
 .
.
Пример. Вычислите  , если
, если  .
.
Решение. Находим тригонометрическую форму числа 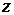 :
:
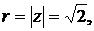
 ,
,  .
.
По формуле Муавра
 .
.
Переходим к алгебраической форме, вычисляя косинус и синус:  .
.
Ответ.  .
.



 . Каждому комплексному числу
. Каждому комплексному числу  можно сопоставить точку с координатами
можно сопоставить точку с координатами 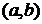 , и наоборот, каждой точке с координатами
, и наоборот, каждой точке с координатами 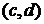 можно сопоставить комплексное число
можно сопоставить комплексное число  . Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью.
. Таким образом, между точками плоскости и множеством комплексных чисел устанавливается взаимно однозначное соответствие. Поэтому комплексные числа можно изображать как точки плоскости. Плоскость, на которой изображают комплексные числа, обычно называют комплексной плоскостью. :
:
 , а именно, комплексное число
, а именно, комплексное число 
 является вектор, равный сумме векторов, изображающих числа
является вектор, равный сумме векторов, изображающих числа 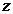 и
и  . Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 11).
. Иными словами, при сложении комплексных чисел складываются и векторы, их изображающие (рис. 11).
 . Из рисунка 12 очевидно, что
. Из рисунка 12 очевидно, что 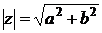 .
.
 , называется аргументом числа
, называется аргументом числа  . Аргумент числа определяется не однозначно, а с точностью до числа, кратного
. Аргумент числа определяется не однозначно, а с точностью до числа, кратного  . Однако, обычно аргумент указывают в диапазоне от
. Однако, обычно аргумент указывают в диапазоне от 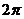 или в диапазоне от
или в диапазоне от  до
до  . Кроме того у числа
. Кроме того у числа  аргумент не определен.
аргумент не определен. . Из того же рисунка очевидно, что
. Из того же рисунка очевидно, что  .
. или
или  ,
, , то комплексное число изображается вектором на оси
, то комплексное число изображается вектором на оси  и его аргумент равен или.
и его аргумент равен или. . Из рисунка 9 очевидно, что
. Из рисунка 9 очевидно, что  .
. . Это выражение запишем в виде
. Это выражение запишем в виде .
. называют иногда алгебраической формой комплексного числа.
называют иногда алгебраической формой комплексного числа. .
.





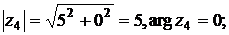
 .
. в степень
в степень  , где
, где  .
. , если
, если  .
.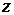 :
: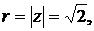
 ,
,  .
. .
. .
. .
.


