

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Подбор подходящих уравнений для поверхности отклика в подавляющем большинстве случаев можно произвести без составления и решения нормальных уравнений типа (1.90) в общем виде. С этой целью можно воспользоваться готовыми формулами. Наиболее характерные формулы и примеры их практического использования, заимствованные из [23], рассмотрены ниже.
Линейная аппроксимация в случае двух переменных. Пусть даны N пар точек хi и уi, приближенно представляющих зависимость
 (1.93)
(1.93)
где b0 - отрезок, отсекаемый данной прямой на оси y, a b1 - угловой коэффициент этой прямой.
Коэффициенты b0 и b1 оцениваются из следующих уравнений
 (1.94)
(1.94)
 (1.95)
(1.95)
Пример. Найти уравнение прямой, аппроксимирующей следующее множество точек:
| x | 2,0 | 4,0 | 6,0 | 8,0 | 10,0 |
| y | 5,5 | 6,3 | 7,2 | 8,0 | 8,6 |
Решение. Пусть уравнение прямой есть  Для вычисления коэффициентов согласно формулам (1.94), (1.95) находим следующие значения:
Для вычисления коэффициентов согласно формулам (1.94), (1.95) находим следующие значения:

Подставляя эти значения в (1.94) и (1.95), находим:
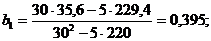

Таким образом, искомое уравнение есть y = 4,75+0,395 x.
Линейная аппроксимация в случае многих переменных. Используем линейную форму для определения соотношения между переменной у и несколькими другими переменными х1, x2, х3,..., хn, записав ее в виде
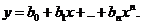 (1.96)
(1.96)
Коэффициенты регрессии b0, bt, b2,..., bn находят из следующих уравнений, связывающих отклонения каждой из величин от их математических ожиданий:


(1.97)

Здесь 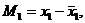

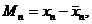


Нелинейная аппроксимация. Между двумя переменными может существовать простая зависимость вида
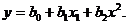 (1.98)
(1.98)
Коэффициенты этого уравнения b0, b1, bsоценивают на основании уравнений

 (1.99)
(1.99)

Пример. Определить уравнение вида y = b0+b1 x+ b2 x2, аппроксимирующее следующее множество точек:
|
|
| x | 2,00 | 4,00 | 6,00 | 8,00 | 10,00 | 12,00 | 14,00 |
| y | 3,76 | 4,44 | 5,04 | 5,56 | 6,00 | 6,36 | 6,64 |
Решение. Вычисляя коэффициенты согласно уравнениям (1.99), найдем:

Подставляя эти значения в соотношения (1.99), получим уравнения:
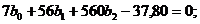
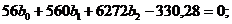
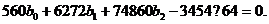
Решая их, определяем b 0 = 3,0; b1 = 0,4; b2 = - 0,01. Искомое уравнение имеет вид

Логарифмическая аппроксимация. Будем отыскивать связь между переменными х, у в виде
 (1.100)
(1.100)
Коэффициенты b0 и b1 находят из уравнений:

(1.101)

Пример. Необходимо аппроксимировать следующее множество точек логарифмической кривой вида (1.100):
| x | ||||||
| y |
Решение. Воспользуемся выражениями (1.101), для которых при N=6 вычисляем:
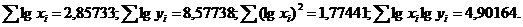
Подставляя эти выражения в соответствующие уравнения, находим


Таким образом, уравнение, соответствующее заданному множеству точек, есть y= 3 x2, где 3 – антилогарифм числа 0,477.
Экспоненциальная аппроксимация. Простейшая экспоненциальная зависимость двух переменных записывается в виде
 . (1.102)
. (1.102)
Коэффициенты b0 и b1 определяются из уравнений:

 (1.103)
(1.103)
где lg e =0,4343.
Один из простых видов экспоненциальной зависимости может быть записан также в форме
 (1.104)
(1.104)
Оценки параметров b0 и b1 эти зависимости могут быть определены из уравнений

(1.105)

Для графического определения типа уравнения наилучшего приближения и значений его коэффициентов строят график по множеству заданных точек, наносимых на бумагу с логарифмической, полулогарифмической или обычной прямоугольной системой координат. Линейный характер графика в какой-либо из перечисленных систем координат говорит об определенном типе аппроксимирующей зависимости.

Рис. 1.26. К примеру.
При необходимости нелинейную функцию можно предварительно привести к линейному виду путем соответствующего преобразования (или разложения в ряд), в частности:
для дробно-линейной зависимости
 (1.106)
(1.106)
для экспоненциальной зависимости
|
|
 (1.107)
(1.107)
или
 (1.108)
(1.108)
где т, ln а и п - постоянные величины;
для тригонометрической зависимости
 (1.109)
(1.109)
где а = A sin α; b =A cos α.
Соответствие между различными системами координат и типами уравнений, изображающимися в них прямой линией, следующее:
| Система координат | Вид уравнения |
| Прямоугольная декартова | у=b0+b1 x |
| Полулогарифмическая | 
|

| |
| Логарифмическая | 
|

| |

|
|
|
|

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!