Метод координат на плоскости.

3.1.1. Найти точку, симметричную точке А (-2;4) относительно биссектрисы первого координатного угла.

Решение:

Рис. 6

Проведем через точку А прямую , перпендикулярную биссектрисе l первого координатного угла (рис.6). Пусть . Нa прямой отложим отрезок , равный отрезку AC. Прямоугольные треугольники АСО и равны между собой (по двум катетам). Отсюда следует, что, . Треугольники ADO и также равны между собой (по гипотенузе и острому углу). Заключаем, что , , т.е. точка 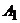имеет координаты х=4, у=-2, т.е. 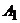(4;-2).

Отметим, что имеет место обще утверждение: точка 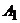, симметричная точке А(a;b) относительно биссектрисы первого и третьего координатных углов, имеет координаты (b;a), т.е.

3.1.2. Дана точка А (3;-2). Найти координаты точек, симметричных точке А относительно оси Ох, оси Оу, начала координат.

3.1.3. Найти координаты точки 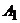, симметричной точке А (2;4) относительно биссектрисы:

1) второго и четвертого координатных углов;

2) первого и третьего координатных углов.

3.1.4. В треугольнике с вершинами А (2;3), В (6;3), С (6;-5) найти длину биссектрисы ВМ.

Решение: По свойству биссектрисы внутреннего угла треугольника (рис.7)

Находим, используя формулу длины сторон ВС и ВА треугольника АВС: , . Следовательно,

 

= = , т.е. =2. Находим координаты и точки

М: = , = ,

рис.7

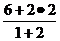т.е. = , = , т.е. М .

Находим длину биссектрисы ВМ: ВМ= 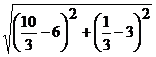= = , т.е.

ВМ= .

 

3.1.5. Доказать, что треугольник с вершинами А(-2;-1), В(6;1),

С(3;4) – прямоугольный.

3.1.6. Точки А(2;4), В(-3;7) и С(-6;6) – три вершины параллелограмма,

причем А и С – противоположные вершины. Найти

четвертую вершину.

3.1.7. Дан треугольник с вершинами А(-2;4), В(-6;8), С(5;-6).

Найти площадь этого треугольника.

3.1.8. Найти точку, в которой прямая, проходящая через точки А(5;5)

и В(1;3), пересечет ось Ох.

Решение: Координаты искомой точки С есть (х;0). А так как точки А, В и С

лежат на одной прямой, то должно выполняться условие

=0 (формула (1.4), площадь

треугольника АВС равна нулю!), где - координаты

точки А, 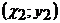- точки В, - точки С. Получаем

(1-5)(0-5)-(х-5)(3-5)=0, т.е. 20+2(х-5)=0, х-5= -10, х= -5.

Следовательно, точка С имеет координаты х= -5, у=0, т.е. С(-5;0).

3.1.9. Доказать, что три точки (2;3), (5;7), (11;15) лежат на одной

прямой.

3.1.10. Разделить отрезок между точками (0;2) и (8;0) в таком же отношении,

в каком находятся расстояния этих точек от начала координат.

3.1.11. На оси ординат найти точку, отстоящую от точки А(3;-8) на

расстоянии 5 единиц.

 

Разное.

3.1.12. Найти длину вектора , соединяющего точки А(-4;5) и В(-6;7), и

угол между этим вектором и положительным направлением оси Ох.

3.1.13. Отрезок с концами А(1;-5) и В(4;3) разделен на три равные части.

Найти координаты точек деления.

3.1.14. Найти координаты центра тяжести однородной пластинки, имеющей

форму треугольника с вершинами в точках А , В(x₂;y₂), C(x₃;y₃) (центр тяжести треугольника находится в точке пересечения его медиан).

3.1.15. Центр тяжести треугольника АВС лежит на оси Ох. Найти координаты вершин С, зная координаты вершин А(3;1) и В(1;-3); площадь треугольника равна 3.

3.1.16. На оси абсцисс найти точку М, расстояние от которой до точки А(1;4) равно 5.

3.1.17. Найти координаты точки, одинаково удаленной от осей координат и от координаты точки А(1;8).

3.1.18. Определить, есть ли среди внутренних углов треугольника с вершинами А(1;1), В(0;2) и С(2;-1) тупой угол.

3.1.19 Даны вершины треугольника: А(7;2), В(1;9), С(-8;-11). Найти расстояние от точки О пересечения медиан треугольника до вершины В.

3.1.20. Две противоположные вершины квадрата находятся в точках А(3;5) и С(1;-3). Найти его площадь.

3.1.21. Найти площадь четырехугольника с вершинами А(-3;2), B(3;4), С(6;1), D(5;-2).

3.1.22. Даны вершины треугольника А(-3;6), В(9;-10), С(-5;4). Найти координаты центра и радиус, описанного около него круга.

3.1.23. Даны вершины А(2;1), В(-2;-2), С(-8;6) треугольника АВС. Найти длину высоты, опущенной из вершины В.

3.1.24. Даны две смежные вершины параллелограмма А(-2;6), В(2;8) и точка пересечения его диагоналей М(2;2). Найти координаты двух других вершин.

3.1.25. Даны середины сторон треугольника М(-1;5), N(1;1), P(4;3). Найти координаты его вершин.

3.1.26. В треугольнике с вершинами О(0;0), А(8;0), В(0;6) определить длины медианы ОС и биссектрисы ОD.

3.1.27. Отрезок с концами А(-8;-8) и В(-2;-4) разделен на 4 равные части. Найти координаты точек деления. До какой точки надо продолжить отрезок АВ, чтобы его длина увеличилась в 3 раза?

3.1.28. Даны точки А(1;2) и В(4;4). На оси Ох найти точку С так, чтобы площадь треугольника АВС была равна 5.

3.1.29. Даны две противоположные вершины квадрата А(3;0) и С(-4;1). Найти координаты двух его других вершин.

3.1.30. Дан треугольник с вершинами А(-√3;1), В(0;2), С(-2√3;2). Найти его внешний угол при вершине А.

3.1.31 Прямая проходит через точки А(2;-3) и В(-6;5). На этой прямой найти абсциссу точки, ордината которой равна -5.

 

3.1.32. Определить центр тяжести однородной пластинки, изображенной на рисунке 8.

 

Рис. 8

 

3.1.33. Определить площадь параллелограмма, три вершины которого – точки A(-2;3), B(4;-5), C(-3;1).

 

3.1.34. В точках М₁(х₁;у₁), М₂(х₂;у₂), М₃(х₃;у₃) помещены массы m₁, m₂, m₃ соответственно. Найти центр тяжести системы. Указание, центр тяжести системы двух масс делит отрезок на части, обратно пропорциональные массам, сосредоточенным на концах отрезка.

3.1.35. Найти положение центра тяжести проволочного треугольника, вершины которого расположены в точках (0;0), (0;3) и (4;0).

3.1.36. Даны вершины однородной треугольной пластинки А (х₁;у₁), В (х₂;у₂), С (х₃;у₃). Если соединить середины ее сторон, то образуется новая треугольная пластинка. Доказать, что центры тяжести обеих пластинок совпадают.

3.1.37. Даны две смежные вершины квадрата А (2;-1) и В (-1;3). Найти координаты двух его других вершин.

3.1.38. Найти координаты центра правильного шестиугольника, зная две его смежные вершины: А(2;0) и В(5;3 ).

3.1.39. Показать, что точки А(-3;8), В(1;5) и С(4;1) могут служить тремя вершинами ромба, вычислить площадь этого ромба.

3.1.40. Прямая линия отсекает на оси Ох отрезок ОА=4 и на оси Оу отрезок ОВ=7. Найти координаты основания перпендикуляра, опущенного из начала координат на данную прямую.

Указание.

3.1.41 В каких четвертях могут быть расположены точки , если

1)

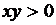
2)

3)

4)

5) ?

3.1.42. Проведем отрезок от точки А(1;-1) до точки (-4;5). Найти координаты точки, до которой нужно продлить его в том же направлении, чтобы длина его удвоилась?

3.1.43. Доказать, что во всяком прямоугольном треугольнике длина медианы,

соединяющей вершину прямого угла с серединой гипотенузы, равна

половине гипотенузы.

3.1.44. Точки А(х₁;у₁) и В(х₂;у₂) служат смежными вершинами ромба, диагонали

которого параллельны осям координат. Как выразить координаты остальных вершин через координаты данных точек?

3.1.45. Как расположены точки, имеющие одну и ту же проекцию на ось Ох? на ось Оу?

3.1.46. Найти прямоугольные координаты точки М с полярными координатами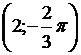

Решение: Имеем Находим: Итак, ).

3.1.47. Найти прямоугольные координаты точек А, В, С, D, E для которых известны полярные координаты А(3;0), ),

3.1.48. Найти полярные координаты точки М с прямоугольными координатами .

Решение: Имеем По формулам (1.6) находим Точка М лежит в III четверти, следовательно, с учетом того, что получаем Итак,

 

3.1.49. Найти полярные координаты точек A, B, C, D, E для которых известны прямоугольные координаты: A(-3;3), B(0;-5), C(-2;-2), D(-4;0), E(;2).

3.1.50. В полярной системе координат заданы точки M₁ (, M₂ (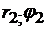). Найти:

а) расстояние между точками M₁ и M₂;

б) площадь треугольника OM₁M₂ (O – полюс).

Решение: а) Найдем расстояние между точками М₁ и М₂ (используем х=rcosφ, y=rsinφ):

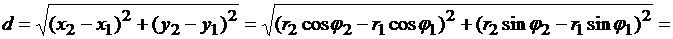
т.е. ;

б) пользуясь формулой для площади треугольника со сторонами a и b и углом между ними , находим площадь треугольника OM₁M_2:

3.1.51. Сторона правильного шестиугольника равна 1. Приняв за полюс одну из его вершин, а за полярную ось – сторону, через нее проходящую, найти полярные координаты остальных пяти вершин.

3.1.52. В полярной системе координат точка пересечения диагоналей параллелограмма ABCD совпадает с полюсом. Зная вершины и найти другие вершины параллелограмма.

 

 

Разное.

3.1.53. В полярной системе координат даны две противоположные вершины квадрата и Найти его площадь.

3.1.54. Одна из вершин треугольника лежит в полюсе полярной системы координат, а другие в точках A(2;0) и Найти радиус вписанной в треугольник окружности.

3.1.55. В полярной системе координат даны точки и Найти полярные координаты середины отрезка, соединяющего эти точки.

3.1.61. Составить управление линии, точки которой равноотстоят от двух заданных точек А (-2;0) и В (4;2).

3.1.62. Найти геометрическое место точек, одинаково удаленных от прямой х =2 и точки F(4;0).

3.1.63. Стержень АВ скользит своими концами по координатным осям. Точка М делит стержень на две части АМ = a и ВМ = b. Найти параметрические управления траектории точки М, приняв в качестве параметра угол .

Решение: Рассмотрим треугольник МСВ (рис.9): в нем 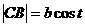, . Очевидно, . Стало быть , 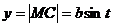. Таким образом, получаем уравнения искомой линии:

 

.

b

Уравнение траектории точки М можно записать виде F (х;у)=0. Для этого перепишем найденные уравнения линии в виде , . Возводя в квадрат полученное равенства и складывая их почленно, получаем:

B

C

O

Рис. 9

x

 

 

Линия, определяемая этим уравнением, называется эллипсом.

3.1.64. Составить уравнение линии, для каждой точки которой расстояние до оси Ох в три раза меньше, чем до оси Оу.

3.1.65. Найти уравнение траектории перемещения точки М, которая движется так, что расстояние от неё до точки всегда равно 5.

3.1.66. В полярной системе координат составить уравнение окружность диаметром а, если полюс системы координат лежит на окружности, а полярная ось проходит через её центр.

		Рис. 10

A

Решение: Пусть – произвольная точка данной окружности. Рассмотрим 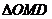(см. рис. 10).

 

в нем |ОМ| = r, <МОА = φ, < МОА = (вписанный угол, опирающийся на диаметр). Поэтому cosφ = . отсюда находим r = acos φ – искомое уравнение окружности.

3.1.67. Составить параметрические уравнения окружности. В качестве параметра t использовать угол между осью Ох и вектором .

3.1.68. Составить уравнение окружности радиуса R, центр которой лежит на прямой, перпендикулярной полярной оси, а полюс системы координат лежит на окружности.

3.1.69. Луч выходит из полюса и наклонен к полярной оси под углом . Составить уравнение этого луча в полярных координатах.

3.1.70. Дана окружность х² +у² = 9. Лежат ли на ней точки М₁ (2√2;1), М₂ (2;3)? Пересекается ли эта окружность с прямой у = 3?

Решение: подставляем координаты точки М₁ в уравнение окружности. Получаем тождество (2√2)²+ 1 = 9. Значит, точка М₁ лежит на окружности. Точка М₂ не лежит на окружности, так как 2² + 3² 9.

Для ответа на второй вопрос решим систему

откуда получаем х = 0 и у = 3. таким образом, окружность и прямая имеют одну общую точку (0;3) – прямая касается окружности.

3.1.71. Указать, какие из данных точек А₁(1;1), А₂ (2;2), А₃ (√3;-1), А₄(; ) лежат на кривой у = 2 – х².

3.1.72. Найти точки пересечения кривой у = 6+5х-х² с осями координат.

3.1.73. Найти точки пересечения линий х + 7у = 25 и х² + у² =25.

3.1.74. На окружности х²+у²=25 найти точки:

а)с абсциссой х=3

б) с ординатой у=у₀

 

3.1.75.В прямоугольных координатах даны параметрические уравнения кривых

а) .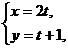

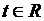б) .

в) .

Найти уравнения заданных кривых в виде F(x;y)=0

3.1.76. Написать уравнение кривой, сумма расстояний от каждой точки которой до точек F₁(-2;0)и F₂(2;0) равна 2 .

3.1.77. Вывести уравнение геометрического места точек, для которых модуль разности расстояний до точек F₁(-4;0) и F₂(4;0) равен 4.

 

 

Прямая на плоскости.

 

3.2.1. Записать уравнение прямой у=2х-3 в отрезках и построить ее.

3.2.2. Определить при каком значении α прямая (α²- α)х+(2+α)у-3α+1=0

а)параллельна оси Ох;

б) проходит через начало координат.

3.2.3. Найти k из условия, что прямая у=kх+2 удалена от начала координат на расстояние .

3.2.4. Написать уравнение прямой, проходящей через точку А и образующей с осью Ох угол, равный аrctg 3.

3.2.5. Уравнение прямой 4х-3у+12=0 представить в различных видах (с угловым коэффициентом, в отрезках, в виде нормального уравнения).

Решение: Для получения уравнения прямой с угловым коэффициентом разрешим заданное уравнение относительно у. Получим 3у=4х+12 и далее у уравнение прямой с угловым коэффициентом; здесь k b=4. Для получения уравнения прямой в отрезках перенесем свободный член С = 12 вправо и разделим обе части уравнения на –12. В результате получим уравнение в отрезках на осях; здесь α =-3, b=4. Приведем исходное уравнение к нормальному виду. Для этого умножим обе части уравнения 4х-3у+12=0 на нормирующий множитель т.е. Перед корнем взят знак «минус», т.к. свободный член (С=12) имеет знак «плюс». Получим т.е. здесь cosα = sinα =

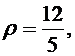
т.е. расстояние от О(0;0) до прямой равно 2,4.

 

3.2.6. Записать уравнение с угловым коэффициентом, в отрезках и нормальное для заданных прямых и определить на каком расстоянии от начала координат они находятся:

а)2х-3у+6=0;

б)х+2,5=0;

в)у=х-1;

г)х+5у=0.

 

3.2.7. Написать уравнение прямой, проходящей через точки:

а) А(0;2),В(-3;7)

б) А(2;1),В(4;1).

Решение: а) Используем уравнение: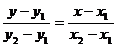

Полагая в нем х =0,у =2, х =-3,

у =7, получим ,

или , т.е

или .

б) Решаем аналогично: . Так как , заключаем что , есть уравнение прямо, проходящей через точки А и В.(Для наглядности построим точки и прямую в системе О - см. рис. 11).

3.2.8. Найти угловой коэффициент к прямой и ординату точки ее пересечения с осью Оу, зная, что прямая проходит через точки А(21;1),В(-2;1).

3.2.9 Прямая проходит через точки А(2;3),В(-4;-1), пересекает ось Оу в точке С. Найти координаты точки С.

3.2.10. Какую абсциссу имеет точка М, лежащая на прямой, проходящей через точки А(-2;-2), В(-1;6), и имеющая ординату, равную 22?

3.2.11 Из пучка прямых, определяемых уравнением y+3=k(x-2)

выделить ту, которая проходит через точку А(-2;5)

Решение: Поставим координат точки А в уравнении прямой:

5+3= к(-2-2), получим к=8: (-4) = -2. Следовательно, искомое

уравнение прямой есть у+3=-2(х-2), т.е. 2х+у-1=0

3.2.12. Найти уравнение прямой:

а) образующей с осью Ох угол 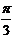и пересекающей ось Оу в точке (0; -6);

б)параллельной оси Ох и отсекающей на оси Оу отрезок, равный 2;

в) отсекающей на осях координат отрезки, равные 3 и 4.

 

3.2.13. Составить уравнение прямой, если точка М (4; 2) является серединой ее отрезка, заключенного между осями координат.

 

3.2.14. Составить уравнение прямой, отсекающей на положительных полуосях координат равные отрезки, если длина отрезка, заключенного между осями координат, равна .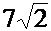

 

3.2.15. Луч света, пройдя через точку А (2; 3) под углом к оси Ох, отразился от нее и прошел через точку В (-5; 4). Найти угол .

 

3.2.16. Луч света направлен по прямой х-у-1=0. Определить точку встречи луча с осью Ох и уравнение прямой, по которой направлен отраженный луч.

 

3.2.17. При каких значениях и прямая отсекает на оси Ох отрезок, равный , а на оси Оу – отрезок, равный (единиц масштаба).

 

3.2.18. Составить уравнение прямой, проходящей через точку А(4;4) и отсекающей от координатного угла треугольник площадью S = 4.

 

3.2.19. Составить уравнение биссектрисы внутреннего угла А треугольника АВС с вершинами А(1;-2), В(5;4), С(-2;0).

 

3.2.20. Составить уравнение прямой, проходящей через точку А(3;-4), являющуюся основанием перпендикуляра, опущенного из начала координат на прямую.

 

3.2.21. Дан треугольник с вершинами А(3;2), В(3;8), С(6;2). Написать уравнение сторон треугольника.

 

3.2.22. Составить уравнение прямой, зная, что расстояние от нее до начала координат равно , а угол между перпендикуляром, опущенным из начала координат на прямую, и осью Ох, равен .

 

3.2.23. Найти площадь треугольника, заключенного между осями координат и прямой

2х-5у+10=0.

3.2.24. Составить (в полярных координатах) уравнение прямой, проходящей через точки и .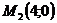

3.2.25. Равнобедренная трапеция с основаниями 10 и 4 имеет острый угол . Написать уравнение сторон трапеции, приняв за ось Ох большее основание, за ось Оу -ось симметрии трапеции.

3.2.26. Через середину отрезка АВ, где А(4; 0), В(0;6), провести прямую, отсекающую на оси Ох отрезок вдвое больший, чем на оси Оу и написать ее уравнение.

3.2.27. Написать уравнение прямой, параллельной биссектрисе второго координатного угла и отсекающей на оси Оу отрезок, равный 3.

3.2.28. При каком значении С прямая 2х-3у+С=0 пересекает ось Оу в точках с ординатами ?

3.2.29. Написать уравнение прямой, проходящей через точку А(2;-1) и параллельной биссектрисе второго координатного угла.

3.2.30. Найти прямую, проходящую через точку пересечения прямых х-2у+3=0 и 2х+у+5=0 и параллельную оси ординат и написать ее уравнения.

3.2.31. Через точку пересечения прямых х+у-6=0 и 2х+у-13=0 провести прямую (несовпадающую с данными), отсекающую на осях равные отрезки и написать ее уравнение.

3.2.32. Составить уравнение прямой, которая проходит через точку М(2;-6) и отсекает на осях Ох и Оу отрезки одинаковой длины(считая каждый отрезок направленным на начала координат).

3.2.33. Через точку М(4;3) проведена прямая, отсекающая от координатного угла треугольник, площадь которого равна 3. Найти точки пересечения этой прямой с осями координат.

3.3.34. Найти угол между прямыми:

1) y=2x-3 и y= x+5;

2) 2x-3y+10=0 и 5x-y+4=0;

3) y= x-2 и 8х+6у+5=0;

4) у=5х+1 и у=5х-2.

1) Воспользуемся формулой: tg . Подставляя в нее значения k₁ = 2 и k_{2 = 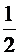,} находим tg φ = , φ = arctg (φ 37⁰);

2) Подставим значение А_{1 =} 2, В₁ = -3, А₂ = 5, В_{2 =} -1 в формулу tg : tg φ = , φ= ;

3) Здесь k₁ = , найдем k₂. Для этого перейдем от 6y = -8x – 5 к эквивалентному равенству

у = - . Здесь к₂ = - . Так как к₁·к₂ = - 1,то данные прямые перпендикулярны.

По формуле: tg получаем:

tg φ = , φ = .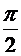

4) к₁ = 5, к₂ = 5, tg φ = 0, φ = 0.

 

3.2.35. Найти угол между двумя прямыми:

1)3х+2у – 1 = 0 и 5х –у + 4=0

2)у=3,5х-3 и 7х-2у+2=0

3) х+4у+10=0 и 5у-3=0

4) 3х-2у+0,1=0 и 2х+3у-5=0

3.2.36. Найти угол между прямыми:

а) х-2=0 и х-у+1=0

б) 2х-3у=0 и прямой, проходящей через точки (5;0) и (0;3).

3.2.37. Исследовать взаимное расположение следующих пар прямых:

1) 3х+5у-9=0 и 10х-6у+4=0

2) 2y+5x-2=0 и х+у+4=0

3) 2х=у-1 и 4у-2х+2=0

4) х+8=0 и 2х-3=0

5) =1 и у =

6) х+у=0 и х-у=0

7) у+3=0 и 2х+у-1=0

8) у=3-6х и 12х+2у-5=0

9) 2х+3у=8 и х+у+3=0

 

10) 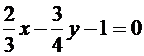и х +

 

3.2.38. При каких значениях α следующие пары прямых: а)паралленльны; б) перпендикурярны?

1)2х – 3у +4 = 0 и αх – 6у + 7 = 0;

2)αх -4у +1 = 0 и -2х + у + 2 =0;

3) 4х+у-6=0 и 3х+aу-2=0

4) х-aу+5=0 и 2х+3у+3=0

3.2.39. Через точку пересечения прямых 3х-2у+5=0, х+2у-9=0 проведена прямая, параллельная прямой 2х+у+6=0. Составить ее уравнение.

Решение: Найдем сначала точку М пересечения данных прямых. Для этого решим систему уравнений:

Отсюда 4х=4. и далее, х=1, у=4, т.е М(1;4). Угловой коэффициент прямой 2х+у-6=0 есть к₁=-2. следовательно, угловой коэффициент к=-2. По направлению прямой (к=-2) и точке М(1;4), ей принадлежащей, запишем уравнение искомой прямой: у-4=-2(х-1), т.е. 2х+у-6=0

3.2.40. Найти уравнение прямой, проходящей через точку А(-1;2):

а) параллельно прямой у=2х-7;

б) перпендикулярно прямой х+3у-2=0

3.2.41. Найти уравнение прямой, проходящей через точку В(2;-3):

а) параллельно прямой, соединяющей точки М₁(-4;0) и М₂(2;2);

б) перпендикулярно прямой х-у=0

3.2.42 Показать, что уравнение прямой, проходящей через точку (х0;у0), и параллельной прямой Ах+Ву+С=0, имеет вид А(х-х0)+В(у-у0)=0.

3.2.43. Показать, что уравнение прямой. проходящей через точку Ах+Ву+С=0, имеет вид А(х-х0)-В(у-у0)=0.

3.2.44. Найти координаты точки М₂, симметричной точке М₁ (-3;4), относительно прямой 4х-у- 1=0.

Рис.12

Решение: Точки М₁и М₂ лежат на прямой М₁,М₂, перпендикулярно прямой 4х-у-1=0, и одинаково удалены от (см.рис. 12, прямая 1). Найдем уравнение прямой М₁М₂. Так как

угловой коэффициент к₁ данной прямой равен 4, то угловой коэффициент к прямой М₁М₂ определяется

 

 

равенствами . Поэтому уравнение прямой М₁М₂

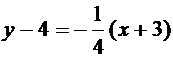, т.е. x+4y-13=0. Найдём координаты точки М – точка пересечения прямой М₁М₂ и данной прямой:

 

 

Отсюда x=1, y=3,т.е. М(1;3). Точка М(1;3) делит отрезок М₁М₂ пополам. Из соотношений и 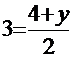находим координаты x и y искомой точки М₂ : x=5,y=2 и М₂ (5;2).

 

3.2.45 Точка А(2;-5) является вершиной квадрата, одна из сторон которого лежит на прямой x-2y-7=0. Найти площадь этого квадрата.

3.2.46 Две стороны квадрата лежат на прямых 5x-12y-65=0 и 5x-12y+26=0. Найти площадь этого квадрата.

3.2.47 Найти уравнение прямой, проходящей через точку A (1;2) так, чтобы расстояние от этой прямой до точек М₁ (2;3) и М₂ (4;-5) были бы равны.

3.2.48 Найти геометрическое место точек, расстояние от которых до прямой 5x-12y-13=0 равно 3.

3.2.49 Написать уравнение прямой l₂ , проходящей через точку A(0;2) под углом к прямой l₁: x-2y+3=0.

Решение: Угловой коэффициент l₁ равен , т.е. k₁= . Обозначим через k угловой коэффициент прямой l₂. Тогда, по формуле tg , имеем tg =1= . Из этого уравнения находим k₂=3 и к₃= - (х-0), т.е. 3х –y+2=0 и x+3y-6=0.

3.2.50 Найти расстояние между параллельными прямыми 3х+4у-20=0 и 6х+8у+5=0

Решение: Возьмем на первой прямой произвольную точку А. Пусть например, х=0, тогда у=5, т.е. А(0;5). Находим расстояние d от точки А до второй прямой:

3.2.51 Найти расстояние между прямыми 2х-3у+8=0 и 4х-6у=10.

3.3.52 Найти длину высоту BD в треугольнике с вершинами А(4;-3), В(-2;6) и С(5;4)

Разное.

3.2.53. Даны уравнения оснований трапеции: 3х – 4у – 15 = 0, 3х - 4у – 35 =0. Найти длину ее высоты.

 

3.2.54 Написать уравнение прямой, проходящей через точку А (1;5) на расстоянии пяти единиц от начала координат.

3.2.55 Найти координаты точки, равноудаленной от двух точек (5;4) и (-3;20 и лежащей на прямой х – 3у + 8 = 0.

3.2.56 Даны две вершины треугольника А (2;-2), В(-6;2) и точка О(1;2) пересечения ее высот. Найти координаты третьей вершины С.

3.2.57 Составить уравнения прямой, содержащей высоту BD в треугольнике с вершинами А(-3;2), В (5;-2), C (0;4).

3.2.58 Найти координаты проекций точки А(1;-3) на прямую 2х – у + 5 = 0.

3.2.59 Найти координаты точки, симметричной точке А(-2;2)относительно прямой х + у = 0.

 

Смешанные задачи на прямую.

 

3.2.60 Найти площадь треугольника, образованного прямыми:2х + у + 4 = 0, х + 7у – 11 =0 и 3х – 5у – 7 = 0.

3.2.61 Составить уравнение прямой, проходящей через точку А (-2;1):

а)параллельно оси Оу;

б)образующей с осью Ох угол ;

в)перпендикулярно вектору ά = (4;2);

г)параллельно биссектрисе первого координатного угла;

д)перпендикулярно прямой 6х – у + 2 = 0;

е)отсекающей от оси Оу отрезок длиной 5.

3.2.62. Через точку пересечения прямых 3х + 2у – 4 =0 и х – 5у + 8 =0 проведены прямые, одна из которых проходит через начало координат, а другая параллельна оси Ох. Составить их уравнения.

3.2.63. Какой угол образует с осью Ох прямая, проходящая через точку D(1;3) и точку пересечения медиан треугольника с вершинами А9-1;4), В (2;3), С(5;8)?

3.2.64. Дан четырехугольник АВСD с вершинами А(3;5), В(6;6), С(5;3), D(1;1). Найти:

а) координаты точки пересечения диагоналей;

б) угол между диагоналями.

 

3.2.65. Луч света, пройдя через точки А(4;6) и В(5;8), упал на прямую х-2у+2=0 и отразился от нее. Составить уравнения прямой, по которой направлен отраженный луч.

 

3.2.66. Известны вершины треугольника А(-2;-4), В(0;1), С(2;-1). Найти расстояние от начала координат до точки пересечения медианы, проведенной из вершина В.

 

3.2.67. Написать уравнения прямых, на которых лежат стороны треугольника АВС, если задана его вершина А(1;3) и уравнения медиан х-2у+1=0 и у-1=0.

 

3.2.68. Найти координаты основания перпендикуляра, опущенного из точки А(-1;2) на прямую 3х-5у-21=0.

 

3.2.69. Дан треугольник с вершинами в точках А(2;5), В(5;-1), С(8;3). составить уравнение прямой, проходящей через точку пересечения медиан треугольника перпендикулярно к прямой х+у+4=0.

 

3.2.70. Известны уравнения прямых, на которых лежат две стороны ромба: х+2у-4=0, х+2у-10=0 и уравнение одного из его диагоналей х-у+2=0. Найти координаты вершин ромба.

 

3.2.71. Дан треугольник с вершинами в точках А(1;-2), В(0;5), С(-6;5). Найти координаты центра описанной около треугольника окружности.

 

3.2.72. Даны две вершины равностороннего треугольника АВС: А(-6;0), В(0;0). Найти координаты:

а) третьей вершины С;

б) центра вписанной в треугольник окружности.

 

3.2.73. Найти уравнения прямых, на которых лежат три стороны квадрата, зная, зная, что четвертой стороной является отрезок прямой 4х+3у-12=0, концы которого лежат на осях координат.

 

3.2.74. Написать уравнение траектории движения точки М(х;у), движущейся так, что сумма расстояний от нее до прямых 2х-у=0 и х+2у=0 остается постоянной и равно .

 

3.2.75. Написать уравнения прямых, на котор<