НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
СОДЕРЖАНИЕ
Введение……………………………………………………
- Частные производные. ……………………………………………………
Указания к задаче 1……………………………………………………
- Производные неявной функции……………………………………………
Указания к задаче 2……………………………………………………
- Дифференциал……………………………………………
Указания к задаче 3……………………………………………………
- Применение дифференциала в приближенных вычислениях значений функций……………………………………………
Указания к задаче 4……………………………………………………
- Формулы Тейлора и Маклорена…………………
Указания к задаче 5……………………………………………………
- Касательная плоскость и нормаль к поверхности…………………
Указания к задаче 6……………………………………………………
- Градиент и производная по направлению…………………
Указания к задаче 7……………………………………………………
- Экстремум функции нескольких переменных …………………
Указания к задаче 8……………………………………………………
Указания к задаче 9……………………………………………………
- Условный экстремум функции нескольких переменных…………………
Указания к задаче 10……………………………………………………
- Наименьшее и наибольшее значение функции…………………
Указания к задаче 11……………………………………………………
- Метод наименьших квадратов……………………………………
Указания к задаче 12……………………………………………………
Указания к задаче 13……………………………………………………
- Расчетные задания………………………………………………
Список литературы…………………………………………………………
Частные производные
Пусть 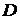 - множество пар
- множество пар 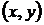 значений независимых переменных
значений независимых переменных 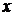 и
и 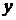 .
.
Определение. Если каждой паре 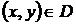 поставлено в соответствие некоторое значение переменной величины
поставлено в соответствие некоторое значение переменной величины 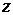 , то говорят, что
, то говорят, что 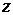 - функция двух независимых переменных
- функция двух независимых переменных 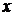 и
и 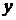 , определенная на множестве
, определенная на множестве 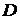 . Множество
. Множество 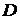 называется областью определения функции
называется областью определения функции 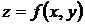 .
.
Определение. Если каждой совокупности 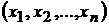 значений независимых переменных
значений независимых переменных 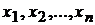 из некоторого множества
из некоторого множества 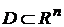 соответствует определенное значение переменной
соответствует определенное значение переменной 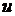 , то говорят, что
, то говорят, что 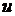 - функция
- функция 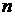 переменных, определенная на множестве
переменных, определенная на множестве 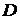 (
( ).
).
Определение. Частной производной функции  по переменной
по переменной 
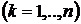 в точке
в точке 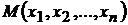 называется предел (если он существует)
называется предел (если он существует)
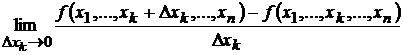 .
.
Обозначается 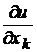 или
или 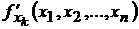 .
.
Для функции 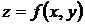 двух переменных по определению имеем
двух переменных по определению имеем
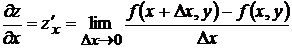 - частная производная по
- частная производная по 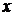 ,
,
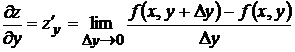 - частная производная по
- частная производная по 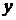 .
.
Замечание. Частные производные вычисляются по обычным правилам и формулам дифференцирования (при этом все переменные, кроме  , рассматриваются как постоянные).
, рассматриваются как постоянные).
Определение. Частными производными 2-го порядка функции  называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Производные второго порядка обозначаются следующим образом:
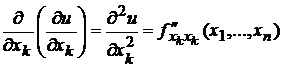 ,
,
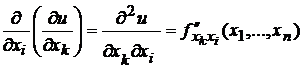 и т.д.
и т.д.
Аналогично определяются и обозначаются частные производные порядка выше второго.
Замечание. Результат многократного дифференцирования функции по различным переменным не зависит от очередности дифференцирования при условии, что возникающие при этом смешанные частные производные непрерывны.
Указания к задаче 1.
Дана функция 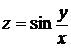 . Показать, что
. Показать, что 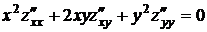 .
.
Решение. Найдем частные производные
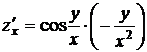 ;
; 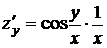 ;
;
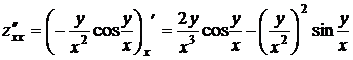 ;
;
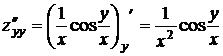 ;
;
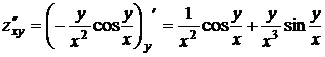 .
.
Подставляя найденные частные производные в левую часть данного уравнения, получим тождество
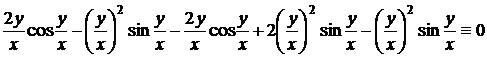 ,
,
что и требовалось доказать.
Производные неявной функции
Частные производные неявной функции  , заданной с помощью уравнения
, заданной с помощью уравнения 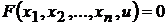 , вычисляются по формулам
, вычисляются по формулам
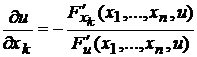
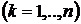 , (2.1)
, (2.1)
при условии, что 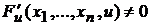 .
.
Производная неявной функции 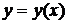 , заданной с помощью уравнения
, заданной с помощью уравнения 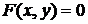 , может быть вычислена по формуле:
, может быть вычислена по формуле:
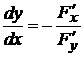 при условии, что
при условии, что 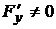 . (2.2)
. (2.2)
Указания к задаче 2.
2.1. Найти первые производные неявной функции, заданной уравнением 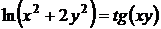 .
.
Решение. Производная неявной функции 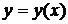 , заданной с помощью уравнения
, заданной с помощью уравнения 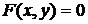 , может быть вычислена по формуле (2.2):
, может быть вычислена по формуле (2.2): 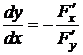 при условии, что
при условии, что 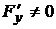 .
.
В данном случае 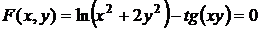 .
. 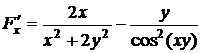 ,
, 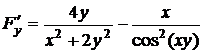 .
.
Найдем производную неявной функции:
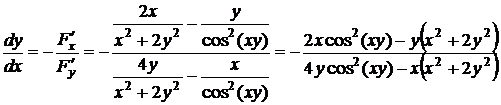 .
.
2.2. Найти первые производные неявной функции, заданной уравнением 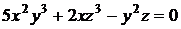 .
.
Решение. Производные неявной функции 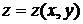 , заданной с помощью уравнения
, заданной с помощью уравнения 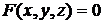 , могут быть вычислены по формуле (2.1):
, могут быть вычислены по формуле (2.1): 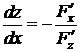 ,
, 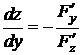 при условии, что
при условии, что 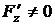 .
.
В данном случае 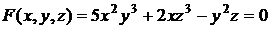 ,
, 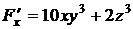 ,
, 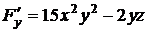 ,
, 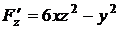 .
.
Найдем производные неявной функции:
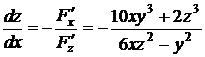 ,
, 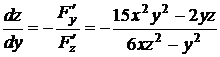 .
.
Дифференциал
Определение. Полным приращением функции  в точке
в точке 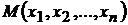 , соответствующим приращениям аргументов
, соответствующим приращениям аргументов  называется разность
называется разность 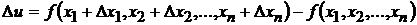 .
.
Определение. Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 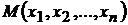 , если в некоторой окрестности этой точки полное приращение функции может быть представлено в виде
, если в некоторой окрестности этой точки полное приращение функции может быть представлено в виде
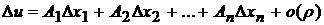 ,
,
где 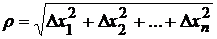 ,
, 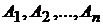 - числа, не зависящие от
- числа, не зависящие от  .
.
Определение. Дифференциалом 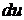 первого порядка функции
первого порядка функции  в точке
в точке 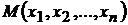 называется главная часть полного приращения этой функции в рассматриваемой точке
называется главная часть полного приращения этой функции в рассматриваемой точке
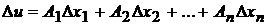 .
.
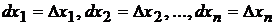 .
.
Для дифференциала функции  справедлива формула
справедлива формула
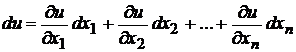 . (3.1)
. (3.1)
Для функции 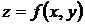 двух переменных имеем
двух переменных имеем
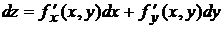 .
.
Дифференциал 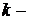 го порядка функции
го порядка функции  выражается символической формулой
выражается символической формулой
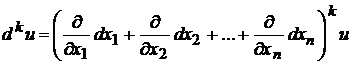 . (3.2)
. (3.2)
Например, в случае функции 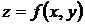 двух переменных для дифференциалов 2-го и 3-го порядков справедливы формулы
двух переменных для дифференциалов 2-го и 3-го порядков справедливы формулы
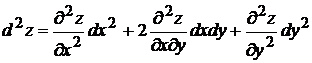 , (3.3)
, (3.3)
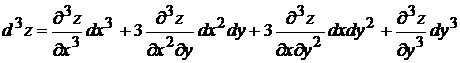 . (3.4)
. (3.4)
Указания к задаче 3.
3.1. Найти дифференциал третьего порядка 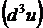 функции
функции 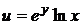 .
.
Решение. Найдем все частные производные до третьего порядка включительно:
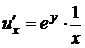 ,
, 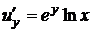 ,
,
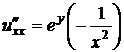 ,
, 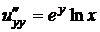 ,
,
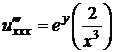 ,
, 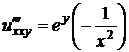 ,
, 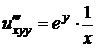 ,
, 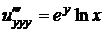 .
.
Найдем дифференциал третьего порядка функции 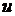 двух переменных по формуле (3.4):
двух переменных по формуле (3.4):
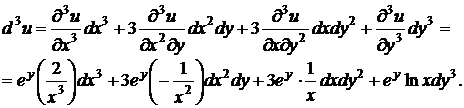
3.2. Найти дифференциал второго порядка 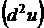 функции
функции  .
.
Решение. Для нахождения дифференциала второго порядка функции трех переменных воспользуемся формулой (3.2):
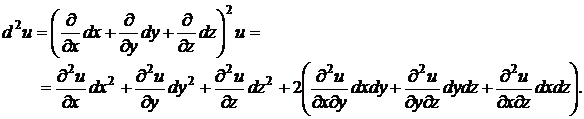
Найдем все частные производные до второго порядка включительно:
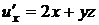 ,
, 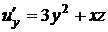 ,
, 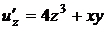 ,
,
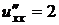 ,
, 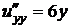 ,
, 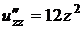 ,
,
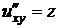 ,
, 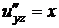 ,
, 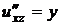 .
.
Найдем дифференциал второго порядка функции 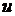 трех переменных:
трех переменных:
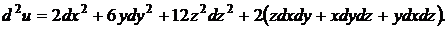
Указания к задаче 4.
Вычислить приближенное значение функции 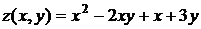 в точке А (3,94; 2,01) .
в точке А (3,94; 2,01) .
Решение. Приближенное значение функции 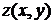 в точке А вычислим, используя формулу (4.1):
в точке А вычислим, используя формулу (4.1):
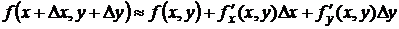
или 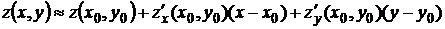 .
.
Вычислим значение функции в точке с координатами 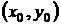 . Если
. Если 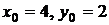 , то
, то 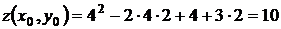 .
.
Так как 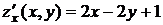 , то
, то 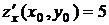 ,
,
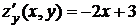 , то
, то 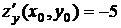 .
.
Подставим в формулу: 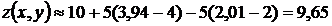 .
.
Формулы Тейлора и Маклорена
Для функции 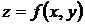 двух переменных формула Тейлора имеет вид
двух переменных формула Тейлора имеет вид
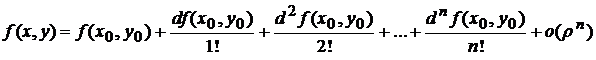 , (5.1)
, (5.1)
где 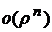 - остаточный член
- остаточный член 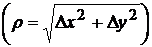 .
.
В частном случае, при 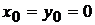 , формула (5.1) называется формулой Маклорена.
, формула (5.1) называется формулой Маклорена.
Указания к задаче 5.
Разложить функцию 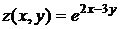 в окрестности точки М(2,1), ограничиваясь членами второго порядка включительно
в окрестности точки М(2,1), ограничиваясь членами второго порядка включительно
Решение. В данном случае формула Тейлора (5.1) принимает вид 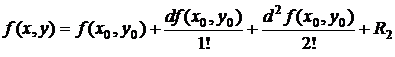 , где
, где 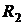 - дополнительный член формулы Тейлора.
- дополнительный член формулы Тейлора.
Найдем значения всех частных производных функции до второго порядка включительно в точке М:
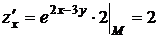 ,
, 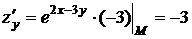 ,
, 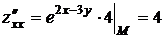 ,
, 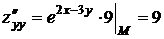 ,
, 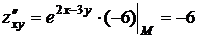 .
.
Составим дифференциалы функции до второго порядка включительно
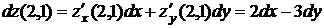 ,
,
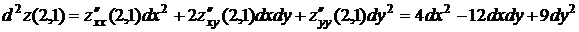 .
.
Учитывая, что 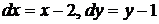 , получим:
, получим:
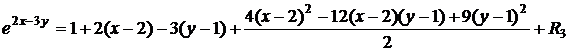 .
.
Указания к задаче 6.
6.1. Составить уравнение касательной плоскости и уравнения нормали к поверхности 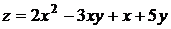 в точке А(1,2,7).
в точке А(1,2,7).
Решение. Если уравнение поверхности задано в явной форме 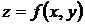 , то уравнение касательной плоскости в точке
, то уравнение касательной плоскости в точке 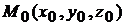 имеет вид (6.1)
имеет вид (6.1)
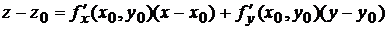 ,
,
а уравнение нормали (6.2) –
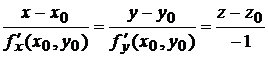 .
.
Найдем значения частных производных 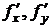 в точке М:
в точке М:
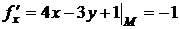 ,
, 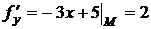 .
.
Подставляя найденные значения в уравнения касательной плоскости и нормали, получим
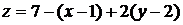 или
или 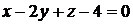 - уравнение касательной плоскости,
- уравнение касательной плоскости, 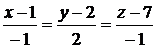 - уравнение нормали.
- уравнение нормали.
6.2. Составить уравнение касательной плоскости и уравнения нормали к поверхности 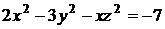 в точке А(1,0,3).
в точке А(1,0,3).
Решение. Если уравнение поверхности задано в неявной форме 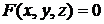 , то уравнение касательной плоскости в точке
, то уравнение касательной плоскости в точке 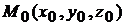 имеет вид (6.3)
имеет вид (6.3)
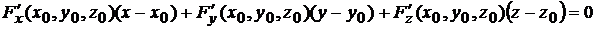 .
.
Уравнение нормали (6.4)
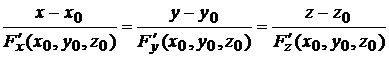 .
.
Найдем значения частных производных 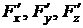 в точке М:
в точке М:
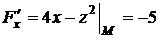 ,
, 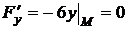 ,
, 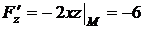 .
.
Подставляя найденные значения в уравнения касательной плоскости и нормали, получим
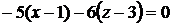 или
или 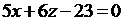 - уравнение касательной плоскости,
- уравнение касательной плоскости, 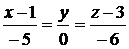 - уравнение нормали.
- уравнение нормали.
Указания к задаче 7.
Даны: функция 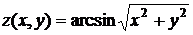 , точка
, точка 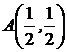 и вектор
и вектор 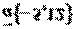 .
.
Найти: 1) 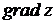 в точке А;
в точке А;
2) производную в точке А по направлению вектора 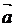 .
.
Решение.
Найдем 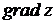 в точке А, для этого вычислим
в точке А, для этого вычислим 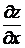 и
и 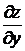 в точке А. Имеем:
в точке А. Имеем:
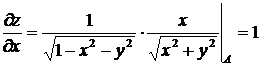 ,
,
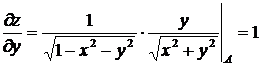 .
.
Таким образом, 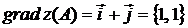 .
.
Для нахождения производной функции 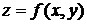 в направлении вектора
в направлении вектора 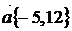 воспользуемсяформулой (7.1). Для этого найдем единичный вектор
воспользуемсяформулой (7.1). Для этого найдем единичный вектор 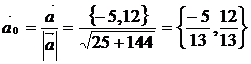 , тогда
, тогда
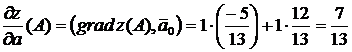 .
.
8. Экстремум функции нескольких переменных
Пусть функция 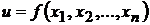 определена в некоторой окрестности точки
определена в некоторой окрестности точки 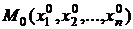 .
.
Определение. Функция  имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 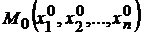 , если существует такая окрестность точки
, если существует такая окрестность точки 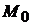 , в которой для всех точек
, в которой для всех точек 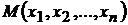 (
(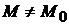 ) выполняется неравенство
) выполняется неравенство 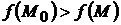 (соответственно
(соответственно 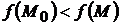 ).
).
Максимум или минимум функции называется ее экстремумом, а точки, в которых функция имеет экстремум, называются точками экстремума (максимума или минимума).
Необходимое условие экстремума. Если функция  имеет экстремум в точке
имеет экстремум в точке 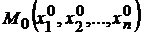 , то в этой точке
, то в этой точке
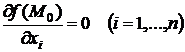 .
.
Точки, в которых выполняются эти условия, называются стационарными точками функции  .
.
Достаточное условие экстремума. Пусть 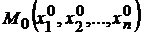 - стационарная точка функции
- стационарная точка функции  , причем эта функция дважды дифференцируема в некоторой окрестности точки
, причем эта функция дважды дифференцируема в некоторой окрестности точки 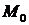 и все ее вторые частные производные непрерывны в точке
и все ее вторые частные производные непрерывны в точке 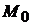 . Тогда:
. Тогда:
 если второй дифференциал
если второй дифференциал 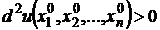
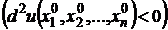 при любых значениях
при любых значениях  , не равных одновременно нулю, то функция
, не равных одновременно нулю, то функция  имеет в точке
имеет в точке 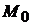 минимум (максимум);
минимум (максимум);
 если
если 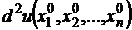 принимает значения разных знаков в зависимости от
принимает значения разных знаков в зависимости от  , то экстремума в точке
, то экстремума в точке 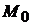 нет;
нет;
 если
если  для набора значений
для набора значений  , не равных нулю одновременно, то требуются дополнительные исследования.
, не равных нулю одновременно, то требуются дополнительные исследования.
Рассмотрим случай функции двух переменных.
Определение. Функция 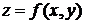 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 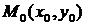 , если существует такая окрестность точки
, если существует такая окрестность точки 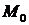 , в которой для всех точек
, в которой для всех точек 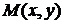 отличных от
отличных от 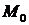 , выполняется неравенство
, выполняется неравенство 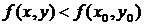
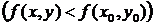 .
.
Необходимое условие экстремума функции двух переменных. Если дифференцируемая функция 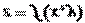 достигает экстремума в точке
достигает экстремума в точке 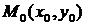 , то в этой точке частные производные первого порядка равны нулю, т.е.
, то в этой точке частные производные первого порядка равны нулю, т.е.
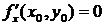 ,
,
 . (8.1)
. (8.1)
Введем обозначения:
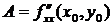 ,
, 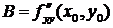 ,
, 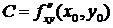 ,
, 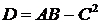 . (8.2)
. (8.2)
Достаточное условие экстремума функции двух переменных. Пусть 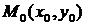 - стационарная точка функции
- стационарная точка функции 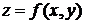 и пусть в окрестности точки
и пусть в окрестности точки 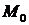 функция имеет непрерывные частные производные второго порядка. Тогда:
функция имеет непрерывные частные производные второго порядка. Тогда:
 если
если 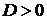 , то функция
, то функция 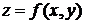 имеет в точке
имеет в точке 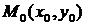 экстремум, а именно максимум при
экстремум, а именно максимум при 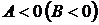 и минимум при
и минимум при 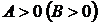 ;
;
 если
если 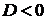 , то экстремум в точке
, то экстремум в точке 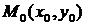 отсутствует;
отсутствует;
 если
если 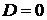 , то требуются дополнительные исследования.
, то требуются дополнительные исследования.
Рассмотрим случай функции 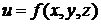 трех переменных.
трех переменных.
Критерий Сильвестра. 1) Для того, чтобы выполнялось неравенство 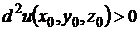 при любых значениях
при любых значениях 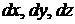 , не равных нулю одновременно, необходимо и достаточно, чтобы:
, не равных нулю одновременно, необходимо и достаточно, чтобы:
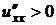 ,
, 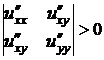 ,
, 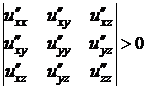 .
.
2) Для того, чтобы выполнялось неравенство  при любых значениях
при любых значениях 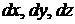 , не равных нулю одновременно, необходимо и достаточно, чтобы:
, не равных нулю одновременно, необходимо и достаточно, чтобы:
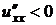 ,
, 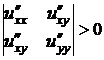 ,
, 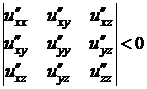 .
.
Следует помнить, что все производные здесь вычислены в точке 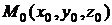 .
.
Указания к задаче 8.
Найти экстремумы функции двух переменных 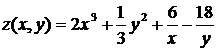 .
.
Решение.
По необходимому условию экстремума, если дифференцируемая функция 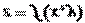 достигает экстремума в точке
достигает экстремума в точке 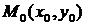 , то в этой точке частные производные первого порядка равны нулю.
, то в этой точке частные производные первого порядка равны нулю.
Найдем стационарные точки функции 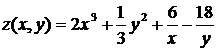 :
:
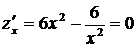 ,
, 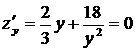 .
.
Решая данную систему, получаем две стационарные точки 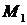 (1,-3),
(1,-3), 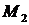 (-1,-3).
(-1,-3).
Воспользуемся достаточным условием экстремума функции двух переменных. По формулам (8.2) найдем 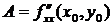 ,
, 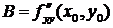 ,
, 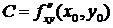 ,
, 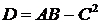 .
.
Рассмотрим точку 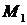 (1,-3):
(1,-3): 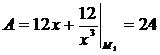 ,
, 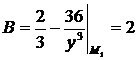 ,
, 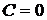 . Так как
. Так как 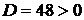 , то точка
, то точка 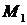 (1,-3) является точкой экстремума, а именно минимума, так как
(1,-3) является точкой экстремума, а именно минимума, так как 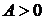 . Найдем минимум функции:
. Найдем минимум функции: 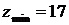 .
.
Рассмотрим точку 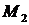 (-1,-3):
(-1,-3): 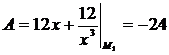 ,
, 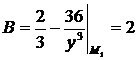 ,
, 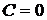 . Так как
. Так как 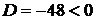 , то в точке
, то в точке 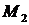 (-1,-3) экстремума нет.
(-1,-3) экстремума нет.
Условный экстремум
Пусть требуется найти экстремум функции 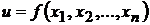 при условии, что
при условии, что 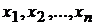 связаны уравнением
связаны уравнением
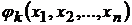 ,
, 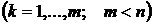 . (9.1)
. (9.1)
Уравнения (9.1) называются уравнениями связи.
Определение. Функция  имеет условный максимум (условный минимум) в точке
имеет условный максимум (условный минимум) в точке 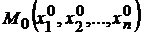 , если существует такая окрестность точки
, если существует такая окрестность точки 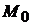 , в которой для всех точек
, в которой для всех точек 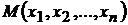 (
(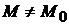 ), удовлетворяющих уравнениям связи, выполняется неравенство
), удовлетворяющих уравнениям связи, выполняется неравенство 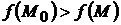 (соответственно
(соответственно 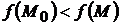 ).
).
Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лагранжа
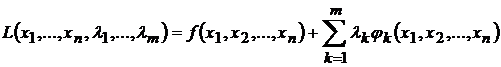 ,
,
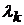
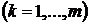 называются множителями Лагранжа.
называются множителями Лагранжа.
Необходимое условие условного экстремума. Если функция  имеет условный экстремум в точке
имеет условный экстремум в точке 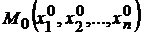 , то в этой точке
, то в этой точке
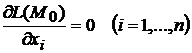 .
.
Для нахождения точки, в которой возможен условный экстремум, составим систему 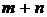 уравнений:
уравнений:
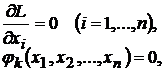 , (9.2)
, (9.2)
из которой найдем неизвестные 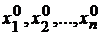 ,
, 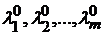 .
.
Достаточное условие условного экстремума. Пусть 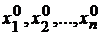 ,
, 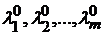 решения системы (9.2), удовлетворяющие уравнениям
решения системы (9.2), удовлетворяющие уравнениям 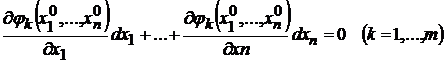 при
при 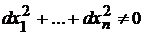 . Функция
. Функция  имеет в точке
имеет в точке 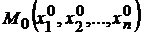 условный максимум, если
условный максимум, если
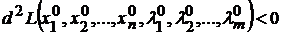
и условный минимум, если
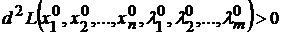 .
.
В случае функции 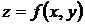 двух переменных при уравнении связи
двух переменных при уравнении связи 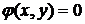 функция Лагранжа примет вид
функция Лагранжа примет вид
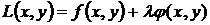 .
.
Система (9.2) запишется в виде
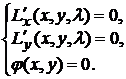
Пусть 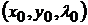 - любое из решений этой системы и
- любое из решений этой системы и
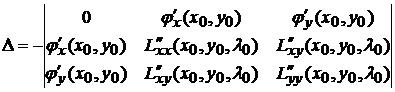 .
.
Тогда, если 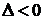 , то функция
, то функция 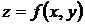 имеет в точке
имеет в точке 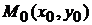 условный максимум; если
условный максимум; если 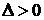 – условный минимум.
– условный минимум.
Указания к задаче 11.
Найти наименьшее и наибольшее значения функции 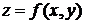 в ограниченной замкнутой области
в ограниченной замкнутой области 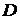 , заданной системой неравенств.
, заданной системой неравенств.
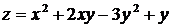 ,
, 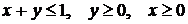 .
.
Решение.
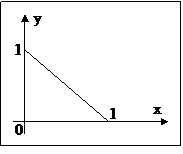 Область
Область 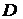 представляет собой треугольник, ограниченный координатными осями и прямой
представляет собой треугольник, ограниченный координатными осями и прямой 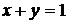 .
.
1) Найдем стационарные точки функции внутри области 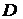 . В этих точках частные производные равны нулю:
. В этих точках частные производные равны нулю:
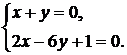
Решая данную систему, получим точку 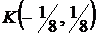 . Эта точка не принадлежит области
. Эта точка не принадлежит области 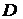 , следовательно, в области
, следовательно, в области 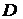 стационарных точек не имеем.
стационарных точек не имеем.
2) Исследуем функцию на границе области. Поскольку граница состоит из трех участков, описываемых тремя различными уравнениями, то будем исследовать функцию на каждом участке отдельно:
· 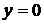 . На этом участке
. На этом участке 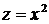
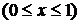 . Так как
. Так как 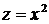 - возрастающая функция переменной
- возрастающая функция переменной 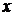 при
при  , то на отрезке
, то на отрезке 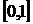 наименьшее значение функции
наименьшее значение функции 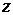 будет в точке (0,0):
будет в точке (0,0): 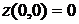 , а наибольшее – в точке (1,0):
, а наибольшее – в точке (1,0): 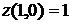 .
.
· 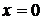 . На этом участке
. На этом участке 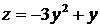
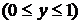 . Найдем производную
. Найдем производную 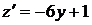 . Из уравнения
. Из уравнения 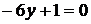 получаем
получаем 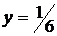 . Таким образом, наибольшее и наименьшее значения функции
. Таким образом, наибольшее и наименьшее значения функции 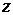 на границе
на границе 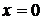 находятся среди ее значений в точках (0,0), (0,1),
находятся среди ее значений в точках (0,0), (0,1), 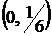 . Найдем эти значения:
. Найдем эти значения:  ,
, 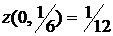 .
.
· 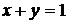 или
или 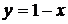 ,
, 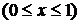 . На этом участке
. На этом участке 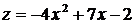 . Решая уравнение
. Решая уравнение 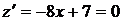 , получим
, получим 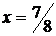 , следовательно,
, следовательно, 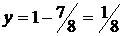 . Значение функции в этой точке равно
. Значение функции в этой точке равно 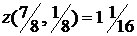 , а на концах отрезка
, а на концах отрезка 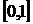 значение функции найдены выше.
значение функции найдены выше.
3) Сравнивая полученные значения 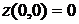 ,
, 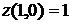 ,
,  ,
, 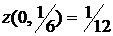 ,
, 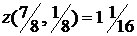 , заключаем, что наибольшее и наименьшее значения функции в замкнутой области
, заключаем, что наибольшее и наименьшее значения функции в замкнутой области 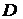 равны соответственно
равны соответственно 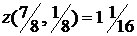 и
и  .
.
11. Метод наименьших квадратов
В различных исследованиях на основании эксперимента требуется установить аналитическую зависимость 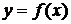 между двумя переменными величинами
между двумя переменными величинами 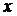 и
и 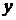 . Широко распространенным методом решения этой задачи является метод наименьших квадратов.
. Широко распространенным методом решения этой задачи является метод наименьших квадратов.
Пусть в результате эксперимента получено 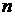 значений функции
значений функции 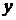 при соответствующих значениях аргумента
при соответствующих значениях аргумента 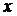 . Результаты сведены в таблицу
. Результаты сведены в таблицу
Вид аппроксимирующей функции 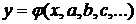 устанавливается или из теоретических соображений, или на основании характера расположения на плоскости точек, соответствующих экспериментальным значениям.
устанавливается или из теоретических соображений, или на основании характера расположения на плоскости точек, соответствующих экспериментальным значениям.
При выбранном виде функции остается подобрать входящие в нее параметры 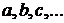 так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.
так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.
Метод наименьших квадратов заключается в следующем. Рассмотрим сумму квадратов разностей значений 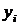 , даваемых экспериментом, и функции
, даваемых экспериментом, и функции 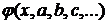 в соответствующих точках:
в соответствующих точках:
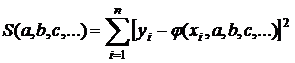 . (11.1)
. (11.1)
Подбираем параметры 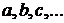 так, чтобы эта сумма имела наименьшее значение. Таким образом, задача свелась к исследованию функции
так, чтобы эта сумма имела наименьшее значение. Таким образом, задача свелась к исследованию функции 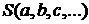 на экстремум.
на экстремум.
Из необходимого условия экстремума функции нескольких переменных следует, что эти значения 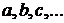 удовлетворяют системе уравнений
удовлетворяют системе уравнений
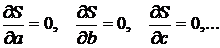 .
.
Или в развернутом виде
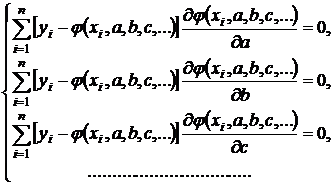 (11.2)
(11.2)
Если требуется найти функцию вида 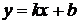 , то функция
, то функция 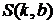 в этом случае имеет вид
в этом случае имеет вид
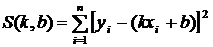 .
.
Это функция с двумя переменными 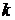 и
и 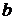 . Исследуем ее на экстремум. Запишем необходимые условия экстремума:
. Исследуем ее на экстремум. Запишем необходимые условия экстремума:
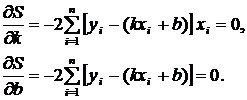
Отсюда получаем следующую систему уравнений относительно неизвестных 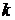 и
и 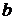
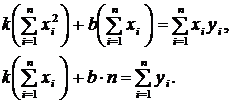 (11.3)
(11.3)
Можно показать, что система (11.3) имеет единственное решение, и при найденных значениях 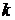 и
и 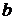 функция
функция 
|
|
|



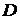 - множество пар
- множество пар 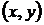 значений независимых переменных
значений независимых переменных 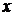 и
и 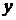 .
.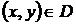 поставлено в соответствие некоторое значение переменной величины
поставлено в соответствие некоторое значение переменной величины 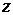 , то говорят, что
, то говорят, что 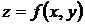 .
.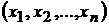 значений независимых переменных
значений независимых переменных 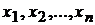 из некоторого множества
из некоторого множества 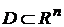 соответствует определенное значение переменной
соответствует определенное значение переменной 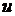 , то говорят, что
, то говорят, что 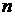 переменных, определенная на множестве
переменных, определенная на множестве  ).
).
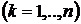 в точке
в точке 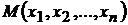 называется предел (если он существует)
называется предел (если он существует)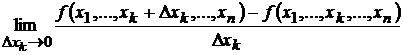 .
.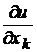 или
или 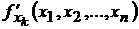 .
.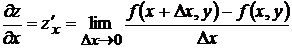 - частная производная по
- частная производная по 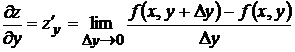 - частная производная по
- частная производная по 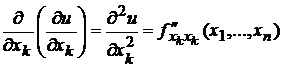 ,
,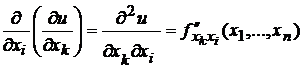 и т.д.
и т.д.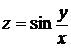 . Показать, что
. Показать, что 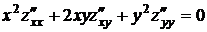 .
.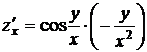 ;
; 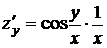 ;
;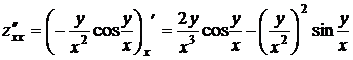 ;
;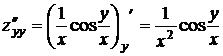 ;
;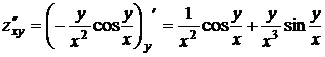 .
.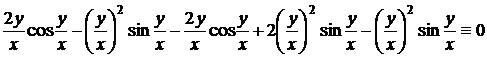 ,
,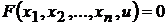 , вычисляются по формулам
, вычисляются по формулам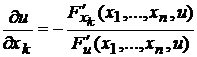
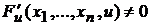 .
.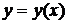 , заданной с помощью уравнения
, заданной с помощью уравнения 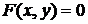 , может быть вычислена по формуле:
, может быть вычислена по формуле: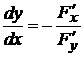 при условии, что
при условии, что 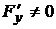 . (2.2)
. (2.2)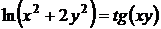 .
.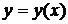 , заданной с помощью уравнения
, заданной с помощью уравнения 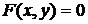 , может быть вычислена по формуле (2.2):
, может быть вычислена по формуле (2.2): 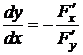 при условии, что
при условии, что 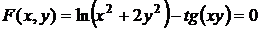 .
. 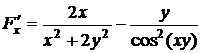 ,
, 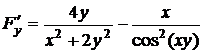 .
.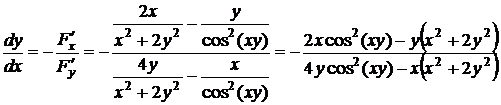 .
.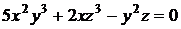 .
.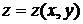 , заданной с помощью уравнения
, заданной с помощью уравнения 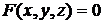 , могут быть вычислены по формуле (2.1):
, могут быть вычислены по формуле (2.1): 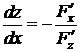 ,
, 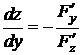 при условии, что
при условии, что 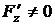 .
.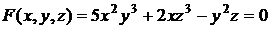 ,
, 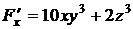 ,
, 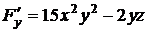 ,
, 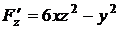 .
.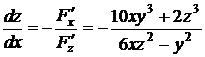 ,
, 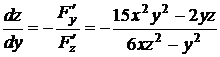 .
. называется разность
называется разность 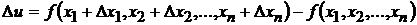 .
.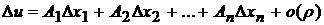 ,
,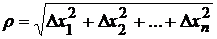 ,
, 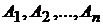 - числа, не зависящие от
- числа, не зависящие от 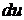 первого порядка функции
первого порядка функции 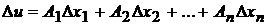 .
.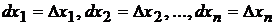 .
.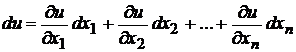 . (3.1)
. (3.1)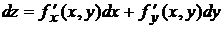 .
.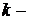 го порядка функции
го порядка функции 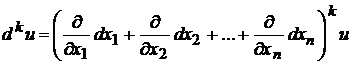 . (3.2)
. (3.2)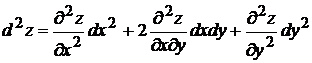 , (3.3)
, (3.3)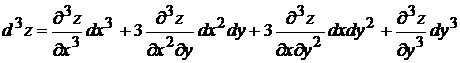 . (3.4)
. (3.4)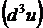 функции
функции 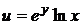 .
.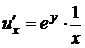 ,
, 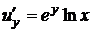 ,
,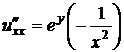 ,
, 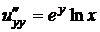 ,
,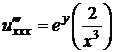 ,
, 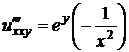 ,
, 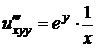 ,
, 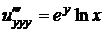 .
.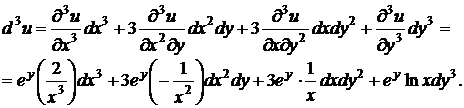
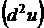 функции
функции  .
.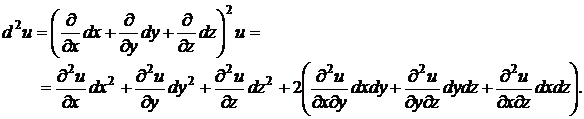
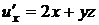 ,
, 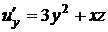 ,
, 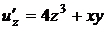 ,
,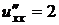 ,
, 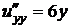 ,
, 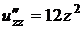 ,
,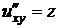 ,
, 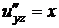 ,
, 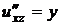 .
.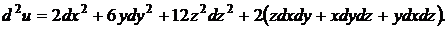
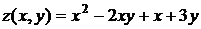 в точке А (3,94; 2,01) .
в точке А (3,94; 2,01) .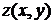 в точке А вычислим, используя формулу (4.1):
в точке А вычислим, используя формулу (4.1):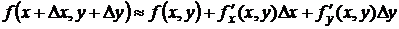
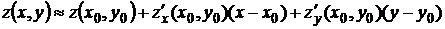 .
.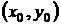 . Если
. Если 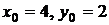 , то
, то 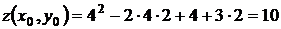 .
.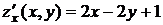 , то
, то 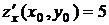 ,
,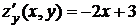 , то
, то 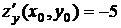 .
.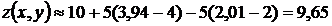 .
.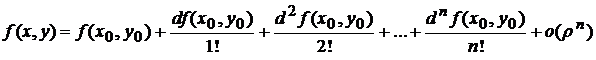 , (5.1)
, (5.1)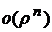 - остаточный член
- остаточный член 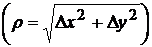 .
.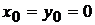 , формула (5.1) называется формулой Маклорена.
, формула (5.1) называется формулой Маклорена.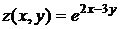 в окрестности точки М(2,1), ограничиваясь членами второго порядка включительно
в окрестности точки М(2,1), ограничиваясь членами второго порядка включительно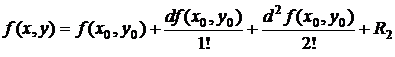 , где
, где 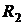 - дополнительный член формулы Тейлора.
- дополнительный член формулы Тейлора.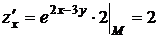 ,
, 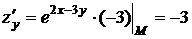 ,
, 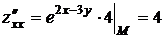 ,
, 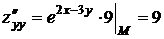 ,
, 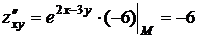 .
.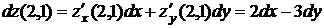 ,
,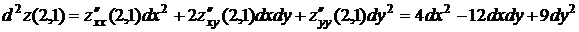 .
.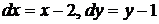 , получим:
, получим: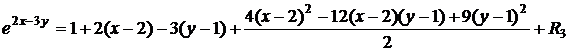 .
.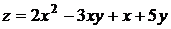 в точке А(1,2,7).
в точке А(1,2,7).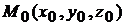 имеет вид (6.1)
имеет вид (6.1)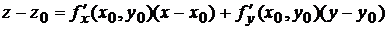 ,
,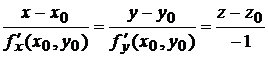 .
.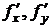 в точке М:
в точке М: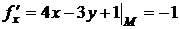 ,
, 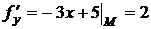 .
.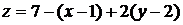 или
или 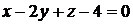 - уравнение касательной плоскости,
- уравнение касательной плоскости, 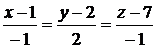 - уравнение нормали.
- уравнение нормали.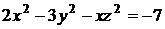 в точке А(1,0,3).
в точке А(1,0,3).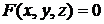 , то уравнение касательной плоскости в точке
, то уравнение касательной плоскости в точке 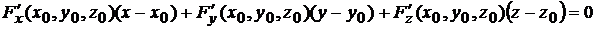 .
.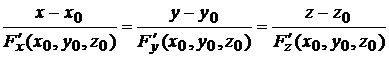 .
.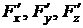 в точке М:
в точке М: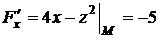 ,
, 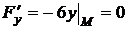 ,
, 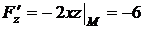 .
.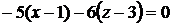 или
или 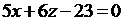 - уравнение касательной плоскости,
- уравнение касательной плоскости, 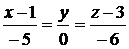 - уравнение нормали.
- уравнение нормали.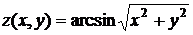 , точка
, точка 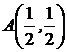 и вектор
и вектор 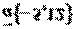 .
.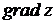 в точке А;
в точке А;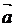 .
.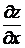 и
и 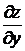 в точке А. Имеем:
в точке А. Имеем: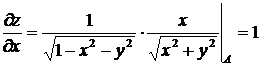 ,
,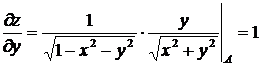 .
.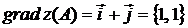 .
.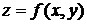 в направлении вектора
в направлении вектора 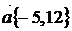 воспользуемсяформулой (7.1). Для этого найдем единичный вектор
воспользуемсяформулой (7.1). Для этого найдем единичный вектор 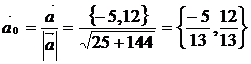 , тогда
, тогда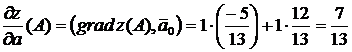 .
.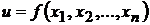 определена в некоторой окрестности точки
определена в некоторой окрестности точки 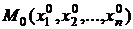 .
.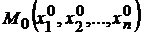 , если существует такая окрестность точки
, если существует такая окрестность точки 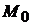 , в которой для всех точек
, в которой для всех точек 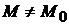 ) выполняется неравенство
) выполняется неравенство 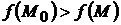 (соответственно
(соответственно 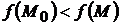 ).
).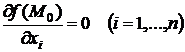 .
.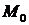 и все ее вторые частные производные непрерывны в точке
и все ее вторые частные производные непрерывны в точке  если второй дифференциал
если второй дифференциал 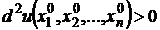
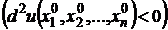 при любых значениях
при любых значениях  , не равных одновременно нулю, то функция
, не равных одновременно нулю, то функция 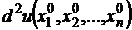 принимает значения разных знаков в зависимости от
принимает значения разных знаков в зависимости от  для набора значений
для набора значений 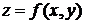 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 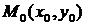 , если существует такая окрестность точки
, если существует такая окрестность точки 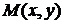 отличных от
отличных от 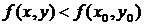
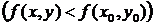 .
.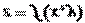 достигает экстремума в точке
достигает экстремума в точке 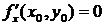 ,
, . (8.1)
. (8.1)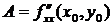 ,
, 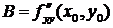 ,
, 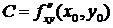 ,
, 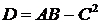 . (8.2)
. (8.2)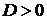 , то функция
, то функция 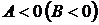 и минимум при
и минимум при 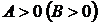 ;
;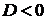 , то экстремум в точке
, то экстремум в точке 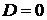 , то требуются дополнительные исследования.
, то требуются дополнительные исследования.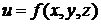 трех переменных.
трех переменных.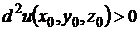 при любых значениях
при любых значениях 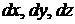 , не равных нулю одновременно, необходимо и достаточно, чтобы:
, не равных нулю одновременно, необходимо и достаточно, чтобы: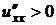 ,
, 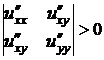 ,
, 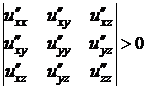 .
. при любых значениях
при любых значениях 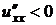 ,
, 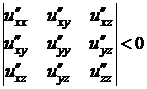 .
.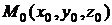 .
.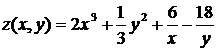 .
.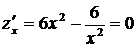 ,
, 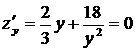 .
.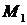 (1,-3),
(1,-3), 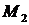 (-1,-3).
(-1,-3).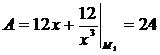 ,
, 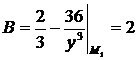 ,
, 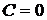 . Так как
. Так как 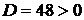 , то точка
, то точка 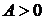 . Найдем минимум функции:
. Найдем минимум функции: 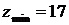 .
.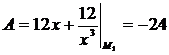 ,
, 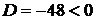 , то в точке
, то в точке 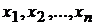 связаны уравнением
связаны уравнением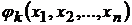 ,
, 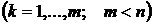 . (9.1)
. (9.1)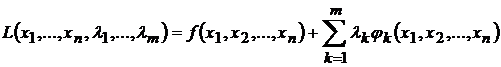 ,
,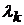
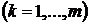 называются множителями Лагранжа.
называются множителями Лагранжа.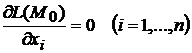 .
.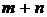 уравнений:
уравнений: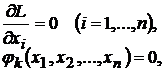 , (9.2)
, (9.2)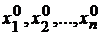 ,
, 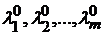 .
.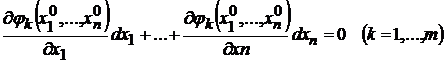 при
при 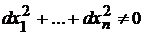 . Функция
. Функция 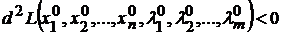
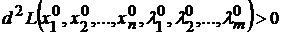 .
.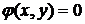 функция Лагранжа примет вид
функция Лагранжа примет вид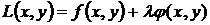 .
.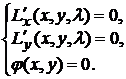
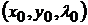 - любое из решений этой системы и
- любое из решений этой системы и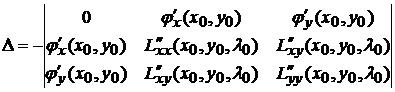 .
.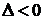 , то функция
, то функция 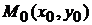 условный максимум; если
условный максимум; если 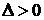 – условный минимум.
– условный минимум.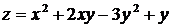 ,
, 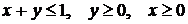 .
. Область
Область 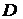 представляет собой треугольник, ограниченный координатными осями и прямой
представляет собой треугольник, ограниченный координатными осями и прямой 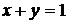 .
.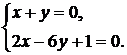
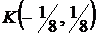 . Эта точка не принадлежит области
. Эта точка не принадлежит области 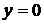 . На этом участке
. На этом участке 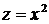
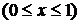 . Так как
. Так как  , то на отрезке
, то на отрезке 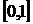 наименьшее значение функции
наименьшее значение функции 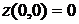 , а наибольшее – в точке (1,0):
, а наибольшее – в точке (1,0): 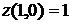 .
.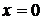 . На этом участке
. На этом участке 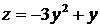
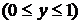 . Найдем производную
. Найдем производную 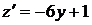 . Из уравнения
. Из уравнения 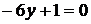 получаем
получаем 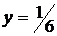 . Таким образом, наибольшее и наименьшее значения функции
. Таким образом, наибольшее и наименьшее значения функции 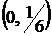 . Найдем эти значения:
. Найдем эти значения:  ,
, 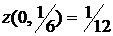 .
.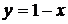 ,
, 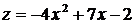 . Решая уравнение
. Решая уравнение 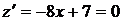 , получим
, получим 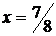 , следовательно,
, следовательно, 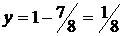 . Значение функции в этой точке равно
. Значение функции в этой точке равно 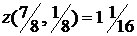 , а на концах отрезка
, а на концах отрезка 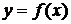 между двумя переменными величинами
между двумя переменными величинами 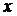 и
и 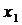
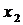
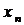
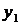
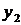
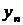
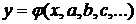 устанавливается или из теоретических соображений, или на основании характера расположения на плоскости точек, соответствующих экспериментальным значениям.
устанавливается или из теоретических соображений, или на основании характера расположения на плоскости точек, соответствующих экспериментальным значениям.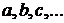 так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.
так, чтобы в каком-то смысле она наилучшим образом описывала рассматриваемый процесс.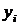 , даваемых экспериментом, и функции
, даваемых экспериментом, и функции 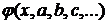 в соответствующих точках:
в соответствующих точках: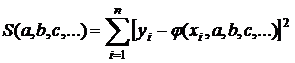 . (11.1)
. (11.1)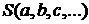 на экстремум.
на экстремум.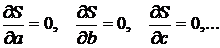 .
.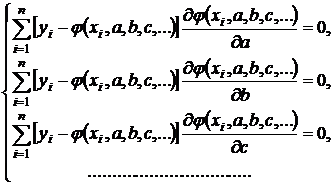 (11.2)
(11.2)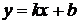 , то функция
, то функция 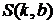 в этом случае имеет вид
в этом случае имеет вид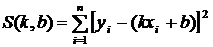 .
.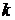 и
и 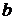 . Исследуем ее на экстремум. Запишем необходимые условия экстремума:
. Исследуем ее на экстремум. Запишем необходимые условия экстремума: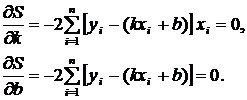
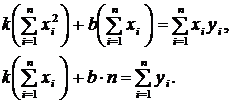 (11.3)
(11.3)

