Произведение равно нулю, если хотя бы один из множителей равен нулю

Примечание: часто разложить на множители удается, если применить формулы преобразования суммы или разности одноименных тригонометрических функций в произведение:
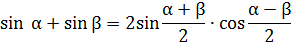
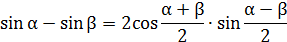
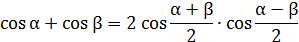


1. Решить уравнение: 
Решение:
Применим формулу: 
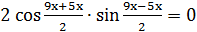 ,
,
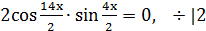 получим
получим  ,
,  отсюда
отсюда




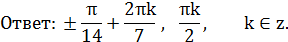
2. Решить уравнение: 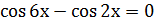
Решение:
Применим формулу: 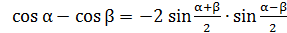 ,
,

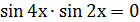 , тогда
, тогда




 , то есть корни , то есть корни  содержатся среди корней содержатся среди корней  . . 
| |

Заметим, что

Методические указания и примеры типового расчёта
Практической работы №7 по теме
«Векторы и координаты. Прямая и её уравнение на плоскости»
Теория
1) Длина стороны треугольника и длина медианы могут быть найдены по формуле расстояние между двумя точками:

Где А 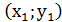 и В
и В  - координаты двух заданных точек.
- координаты двух заданных точек.
2) Координаты вектора 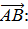
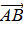 = (
= (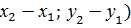
3) Длина вектора равна корню квадратному из суммы квадратов его координат:
 , где
, где  .
.
4) Центром тяжести треугольника является точка пересечения его медиан. Точка пересечения медиан любого треугольника делит каждую медиану в отношении 2:1.
Тогда из формул «деление отрезка в данном отношении»:
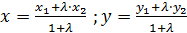 , где
, где 
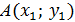





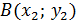

При 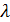 = 2 получим формулы для определения координат точки пересечения медиан треугольника:
= 2 получим формулы для определения координат точки пересечения медиан треугольника:

5) Площадь треугольника находится по формуле: 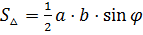
Косинус угла 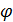 при вершине треугольника можно найти исходя из определения скалярного произведения двух векторов:
при вершине треугольника можно найти исходя из определения скалярного произведения двух векторов:
 , откуда
, откуда 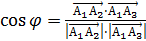
Скалярное произведение двух векторов равно сумме произведений их одноименных координат:

 , где
, где  ,
,  - координаты векторов.
- координаты векторов.
Из основного тригонометрического тождества
 следует, что
следует, что 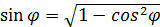
6) Для составления уравнений сторон и медиан треугольника нужно применить уравнение прямой, проходящей через две заданные точки 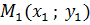 и
и 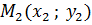 :
:
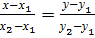 , а затем, преобразовав это уравнение,
, а затем, преобразовав это уравнение,
получить общее уравнение прямой 
Координаты середины отрезка находят по формулам (при  :
:
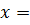
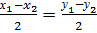
7) Для составления высоты  нужно применить уравнение прямой, проходящей через заданную точку
нужно применить уравнение прямой, проходящей через заданную точку  с заданным нормальным вектором
с заданным нормальным вектором 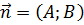 :
:

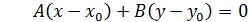
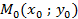

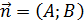
8) Для нахождения длины высоты  можно применить формулу: расстояние от точки до прямой:
можно применить формулу: расстояние от точки до прямой:
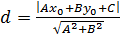 , где
, где 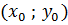 - координаты точки;
- координаты точки;
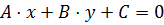 - общее уравнение прямой.
- общее уравнение прямой.
Пример 1: Дан 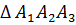 c вершинами
c вершинами 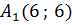 ,
, 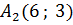 ,
, 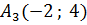 .
.
Найти: 1) Длины сторон треугольника; 2) Длины его медиан; 3) Координаты центра тяжести; 4) Площадь треугольника; 5) Угол при вершине 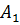 ; 6) Составить уравнения сторон треугольника; 7) составить уравнения медиан треугольника; 8) составить уравнение высоты
; 6) Составить уравнения сторон треугольника; 7) составить уравнения медиан треугольника; 8) составить уравнение высоты  , опущенной из вершины
, опущенной из вершины 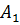 треугольника; 9) найти длину высоты
треугольника; 9) найти длину высоты  . Сделать чертёж.
. Сделать чертёж.
Решение:
1) Найдем длины сторон  по формуле
по формуле  :
:
 = 3 (ед.дл.);
= 3 (ед.дл.);
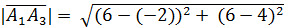 =
= 
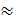 8,25 (ед.дл.);
8,25 (ед.дл.);
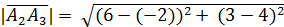 =
= 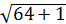 =
=  7,69 (ед.дл.).
7,69 (ед.дл.).
2)Найдем координаты середин сторон треугольника по формуле M 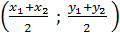
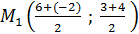 ,
, 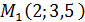 ;
;
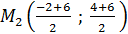 ,
, 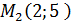 ;
;
 ,
, 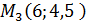 .
.
Тогда длины медиан: 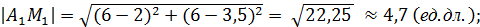


3) Координаты центра тяжести, т.е.координаты точки пересечения медиан треугольника, найти по формулам: 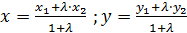 , где
, где 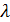 =2:1=2, тогда
=2:1=2, тогда
 ;
;  .
.
Возьмём медиану 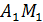 :
:  ,
, 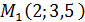 , тогда
, тогда
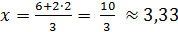 ;
; 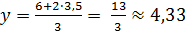 ; значит, координаты центра тяжести треугольника:
; значит, координаты центра тяжести треугольника:

4)Площадь  найдем по формуле:
найдем по формуле:  .
.
Здесь 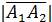 =3,
=3, 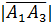 =
= 
Найти 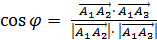 .
.
Координаты векторов найдем по формуле 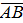 = (
= (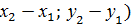 :
:
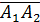 =
= 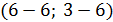 = (0;-3);
= (0;-3);
 =
= 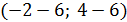 = (-8;-2).
= (-8;-2).
Скалярное произведение векторов находим по формуле:  .
.
Тогда, 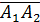
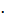
 = 0
= 0 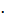 (-8)+ (-3)
(-8)+ (-3) 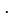 (-2)= 6
(-2)= 6
Значит,  . Отсюда
. Отсюда 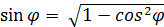 ,
,
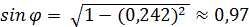
Следовательно, 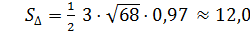 (кв. ед. дл).
(кв. ед. дл).
5) Найдем угол при вершине  . Он заключен между векторами
. Он заключен между векторами 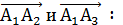
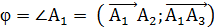 ,
, 
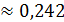 ,
,
Тогда  arccos 0,242
arccos 0,242  .
.
6) Составим уравнение сторон ∆  . Применим уравнение прямой, проходящей через две заданные точки:
. Применим уравнение прямой, проходящей через две заданные точки:  .
.
Сторона  :
:  (6;6),
(6;6),  (6;3), тогда
(6;3), тогда
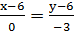 ; x-6=0, x=6 –общее уравнение стороны
; x-6=0, x=6 –общее уравнение стороны 
Сторона  :
: 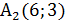 ,
, 
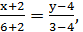 отсюда
отсюда  -1(x+2)=8(y-4), -x-2=8y-32,
-1(x+2)=8(y-4), -x-2=8y-32,
-x-2-8y+32=0, -x-8y+30=0, умножить обе части уравнения на (-1):
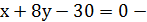 общее уравнение стороны
общее уравнение стороны 

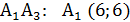 ,
, 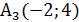
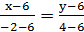 , отсюда
, отсюда  – общее уравнение стороны
– общее уравнение стороны 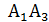 .
.
7) Составим уравнение медиан ∆ 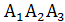 :
:
Медиана 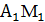 : подставим координаты точки
: подставим координаты точки  ),
), 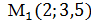 в уравнение прямой, проходящей через две заданные точки:
в уравнение прямой, проходящей через две заданные точки:  =
= 
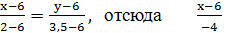 =
= 
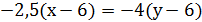 ,
,
 , умножим обе части ур. на (-2):
, умножим обе части ур. на (-2):
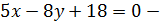 общее уравнение медианы
общее уравнение медианы 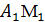 .
.
Медиана 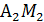 :
: 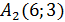 ,
, 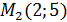
 =
=  отсюда
отсюда 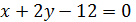 - общее уравнение медианы
- общее уравнение медианы 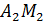
Медиана 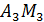 :
: 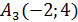 ,
, 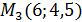
 , отсюда
, отсюда 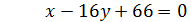 - общее уравнение медианы
- общее уравнение медианы 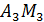
8) Для высоты  опущенной из вершины
опущенной из вершины 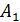 треугольника, нормальнымвектором является вектор
треугольника, нормальнымвектором является вектор  Найдем его координаты:
Найдем его координаты:
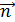 =
= 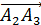 = (-2-6; 4-3)=(-8;1)
= (-2-6; 4-3)=(-8;1)
Подставим координаты нормального вектора  =(-8;1) и координаты точки
=(-8;1) и координаты точки 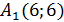 в уравнении прямой с заданным нормальным вектором
в уравнении прямой с заданным нормальным вектором
А(x- 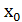 )+B(y-
)+B(y- 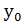 )=0:
)=0:
-8(x-6)+1(y-6)=0, отсюда-8x+y+42=0, умножим части уравнения на (-1):
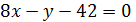 - общее уравнение высоты
- общее уравнение высоты 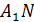 .
.
9) Длина высоты  равна расстоянию от точки
равна расстоянию от точки 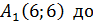 прямой
прямой  , общее уравнение которой имеет видx+8y-30=0.Подставим эти данные вформулу нахождения расстояния от точки
, общее уравнение которой имеет видx+8y-30=0.Подставим эти данные вформулу нахождения расстояния от точки 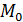 (
(  ;
;  ) до прямой Ax+By+С=0:
) до прямой Ax+By+С=0:
d=  , имеем d=
, имеем d= 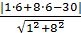 =
=  ( ед.дл.)
( ед.дл.)
Длину высоты 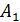 N можно найти и другим способом. Найдем координаты точки
N можно найти и другим способом. Найдем координаты точки 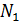 , которая является точкой пересечения прямых
, которая является точкой пересечения прямых 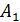 N и
N и 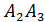 .
.
Для этого решимсистему двух линейных уравнений:
 ,
,  ,
, 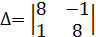 =64+1=65,
=64+1=65,
 =
= 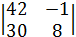 =336+30=366,
=336+30=366,
∆y= 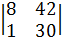 =240-42=198; по формулам Крамера: x=
=240-42=198; по формулам Крамера: x= 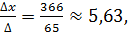
y= 
Итак, N (5,63;3,05).
Длину высоты  N найдем по формуле "расстояние между двумя точками": |AB|=
N найдем по формуле "расстояние между двумя точками": |AB|= 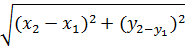 , тогда получим:
, тогда получим:
d=| 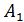 N|=
N|= 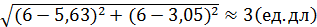
Ответ: 1) 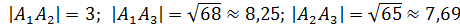 ;
;
2)  ;
; 
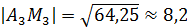 ;
;
3)  ;
;
4)  ;
;
5) 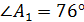 ;
;
6)  уравнение стороны
уравнение стороны 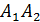 ;
;
 уравнение стороны
уравнение стороны  ;
;
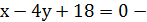 уравнение стороны
уравнение стороны 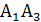 ;
;
7)  уравнение медианы
уравнение медианы 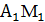 ;
;
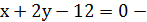 уравнение медианы
уравнение медианы 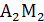 ;
;
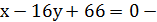 уравнение медианы
уравнение медианы  ;
;
8) 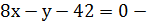 уравнение высоты
уравнение высоты 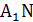 ;
;
9) d=  .
.
Пример 2. Дано:  АВС, А(6;5), В(1;-3), С(-4;2).
АВС, А(6;5), В(1;-3), С(-4;2).
Составить: 1)уравнение стороны ВС; 2)уравнение медианы AF; 3) Уравнение высоты СЕ. Найти: 4) угол между медианой AF и высотой СЕ.
Сделать чертеж.
Решение:
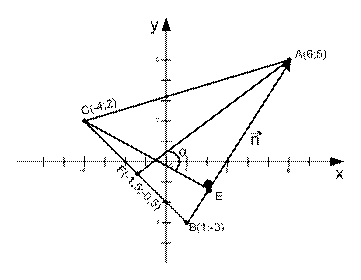
1) Составим уравнение стороны ВС, применим уравнение прямой проходящей через две заданные точки:
 , где В(1;-3), С(-4;2). Тогда
, где В(1;-3), С(-4;2). Тогда


5(x-1)=-5(y+3),
5x-5=-5y+15,
5x-5+5y+15=0:/5,
x+y+2=0 – общее уравнение стороны ВС.
2)Найдем координаты точки F- середины отрезка ВС по формуле середина отрезка:
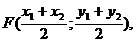 где В(1;-3), С(-4;2).
где В(1;-3), С(-4;2). 
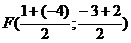 , F(-1,5;-0,5).
, F(-1,5;-0,5).
Составим уравнение медианы AF, применим уравнение прямой проходящей через две заданные точки:
 , где A(6;5), F(-1,5;-0,5). Тогда
, где A(6;5), F(-1,5;-0,5). Тогда
 ,
,
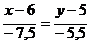 ,
,
-5,5⋅(x-6)=-7,5(y-5),
-5,5x+33=-7,5y+37,5,
-5,5x+ 33 +7,5y- 37,5 =0,
-5,5x+7,5y-4,5=0⋅/-2
11x-15y+9=0-общее уравнение медианы AF
3) Составим уравнение высоты СЕ треугольника, применим уравнение прямой, проходящей через заданную точку с заданным нормальном вектором:
А⋅(x-x0)+B⋅(y-y0)=0, где заданной точкой является точка С(-4;2).
Нормальным вектором для высоты СЕ является вектор  .
.
Найдем его координаты:
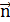 =
=  =
= 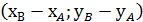
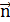 =
=  =(1-6;-3-5)
=(1-6;-3-5)
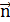 = (-5;-8), значит A= -5; В= -8. Тогда получим
= (-5;-8), значит A= -5; В= -8. Тогда получим
-5⋅(x-(-4))+(-8)⋅(y-2)=0,
-5⋅(х+4)-8⋅(у-2)=0,
-5x -20-8y+16=0,
-5x-8y-4=0⋅/-1
5x+8y+4=0 – общее уравнение высоты СЕ.
4) Чтобы найти угол между медианой AF и СЕ, нужно сначала перевести их уравнения из общего уравнения прямой в уравнение прямой с угловым коэффициентом k:
AF: 11x – 15y + 9 =0, отсюда:
-15y=-11x-9:/-15
у =  ,
,
у = 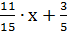 , k1 =
, k1 =  - угловой коэффициент медианы AF.
- угловой коэффициент медианы AF.
Для СЕ:
5x +8y+4=0, отсюда
8y=-5x-4:/8
y= 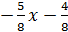 , k2=
, k2= 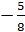 - угловой коэффициент высоты CE.
- угловой коэффициент высоты CE.
Находим угол по формуле:
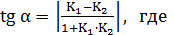 k1=
k1=  , k2=
, k2= 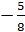


Ответ: 1) х+у+2=0; 2) 11х-15у+9=0; 3) 5х+8у+4=0; 4)  .
.
Методические указания и примеры типового расчёта




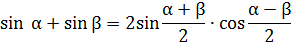
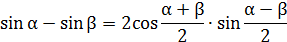
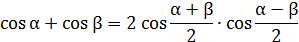




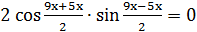 ,
,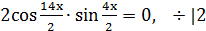 получим
получим  ,
,  отсюда
отсюда



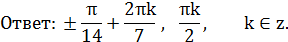
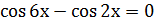
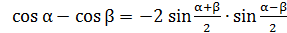 ,
,
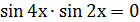 , тогда
, тогда



 , то есть корни
, то есть корни  содержатся среди корней
содержатся среди корней  .
. 
 Заметим, что
Заметим, что


 и В
и В  - координаты двух заданных точек.
- координаты двух заданных точек.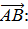
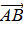 = (
= (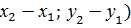
 , где
, где  .
.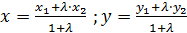 , где
, где 
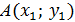




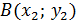

 = 2 получим формулы для определения координат точки пересечения медиан треугольника:
= 2 получим формулы для определения координат точки пересечения медиан треугольника:
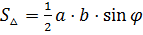
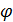 при вершине треугольника можно найти исходя из определения скалярного произведения двух векторов:
при вершине треугольника можно найти исходя из определения скалярного произведения двух векторов: , откуда
, откуда 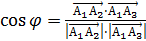
 , где
, где  ,
,  - координаты векторов.
- координаты векторов. следует, что
следует, что 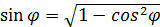
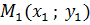 и
и 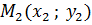 :
: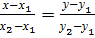 , а затем, преобразовав это уравнение,
, а затем, преобразовав это уравнение,
 :
: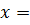
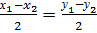
 нужно применить уравнение прямой, проходящей через заданную точку
нужно применить уравнение прямой, проходящей через заданную точку  с заданным нормальным вектором
с заданным нормальным вектором 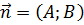 :
:

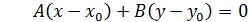
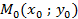

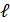
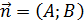
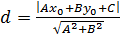 , где
, где 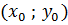 - координаты точки;
- координаты точки;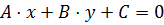 - общее уравнение прямой.
- общее уравнение прямой.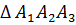 c вершинами
c вершинами 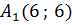 ,
, 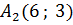 ,
, 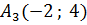 .
.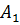 ; 6) Составить уравнения сторон треугольника; 7) составить уравнения медиан треугольника; 8) составить уравнение высоты
; 6) Составить уравнения сторон треугольника; 7) составить уравнения медиан треугольника; 8) составить уравнение высоты  , опущенной из вершины
, опущенной из вершины  по формуле
по формуле  :
: = 3 (ед.дл.);
= 3 (ед.дл.);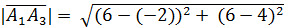 =
= 
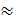 8,25 (ед.дл.);
8,25 (ед.дл.);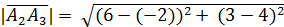 =
= 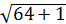 =
=  7,69 (ед.дл.).
7,69 (ед.дл.).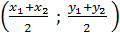
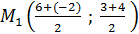 ,
, 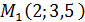 ;
;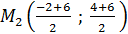 ,
, 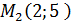 ;
; ,
, 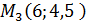 .
.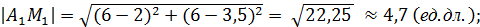


 ;
;  .
.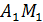 :
:  ,
, 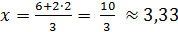 ;
; 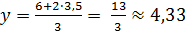 ; значит, координаты центра тяжести треугольника:
; значит, координаты центра тяжести треугольника:
 .
.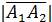 =3,
=3, 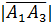 =
= 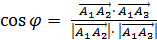 .
.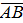 = (
= (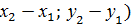 :
: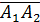 =
= 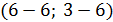 = (0;-3);
= (0;-3); =
= 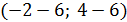 = (-8;-2).
= (-8;-2).
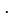 (-2)= 6
(-2)= 6 . Отсюда
. Отсюда 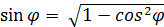 ,
,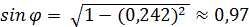
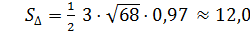 (кв. ед. дл).
(кв. ед. дл). . Он заключен между векторами
. Он заключен между векторами 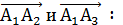
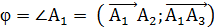 ,
, 
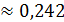 ,
, arccos 0,242
arccos 0,242  .
.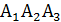 . Применим уравнение прямой, проходящей через две заданные точки:
. Применим уравнение прямой, проходящей через две заданные точки:  .
. :
:  (6;3), тогда
(6;3), тогда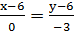 ; x-6=0, x=6 –общее уравнение стороны
; x-6=0, x=6 –общее уравнение стороны 
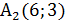 ,
, 
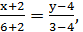 отсюда
отсюда  -1(x+2)=8(y-4), -x-2=8y-32,
-1(x+2)=8(y-4), -x-2=8y-32,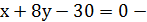 общее уравнение стороны
общее уравнение стороны 

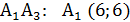 ,
, 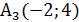
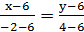 , отсюда
, отсюда  – общее уравнение стороны
– общее уравнение стороны 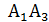 .
.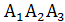 :
: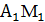 : подставим координаты точки
: подставим координаты точки  ),
), 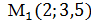 в уравнение прямой, проходящей через две заданные точки:
в уравнение прямой, проходящей через две заданные точки:  =
= 
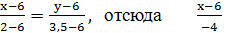 =
= 
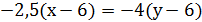 ,
, , умножим обе части ур. на (-2):
, умножим обе части ур. на (-2):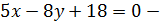 общее уравнение медианы
общее уравнение медианы  .
.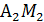 :
: 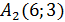 ,
, 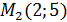
 =
=  отсюда
отсюда 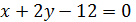 - общее уравнение медианы
- общее уравнение медианы 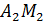
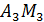 :
: 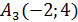 ,
, 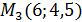
 , отсюда
, отсюда 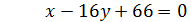 - общее уравнение медианы
- общее уравнение медианы  опущенной из вершины
опущенной из вершины 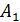 треугольника, нормальнымвектором является вектор
треугольника, нормальнымвектором является вектор  Найдем его координаты:
Найдем его координаты: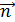 =
= 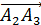 = (-2-6; 4-3)=(-8;1)
= (-2-6; 4-3)=(-8;1) =(-8;1) и координаты точки
=(-8;1) и координаты точки 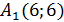 в уравнении прямой с заданным нормальным вектором
в уравнении прямой с заданным нормальным вектором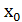 )+B(y-
)+B(y- 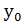 )=0:
)=0: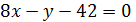 - общее уравнение высоты
- общее уравнение высоты 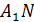 .
. равна расстоянию от точки
равна расстоянию от точки 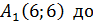 прямой
прямой  , общее уравнение которой имеет видx+8y-30=0.Подставим эти данные вформулу нахождения расстояния от точки
, общее уравнение которой имеет видx+8y-30=0.Подставим эти данные вформулу нахождения расстояния от точки  (
(  ;
;  ) до прямой Ax+By+С=0:
) до прямой Ax+By+С=0: , имеем d=
, имеем d= 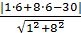 =
=  ( ед.дл.)
( ед.дл.)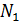 , которая является точкой пересечения прямых
, которая является точкой пересечения прямых 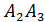 .
. ,
,  ,
, 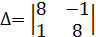 =64+1=65,
=64+1=65, =
= 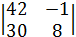 =336+30=366,
=336+30=366,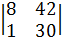 =240-42=198; по формулам Крамера: x=
=240-42=198; по формулам Крамера: x= 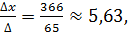

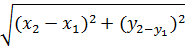 , тогда получим:
, тогда получим: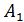 N|=
N|= 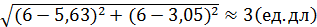
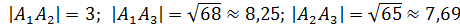 ;
; ;
; 
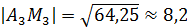 ;
; ;
; ;
;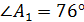 ;
; уравнение стороны
уравнение стороны 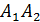 ;
; уравнение стороны
уравнение стороны  ;
;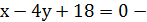 уравнение стороны
уравнение стороны 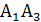 ;
; уравнение медианы
уравнение медианы 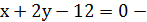 уравнение медианы
уравнение медианы 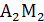 ;
;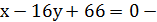 уравнение медианы
уравнение медианы  ;
;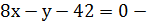 уравнение высоты
уравнение высоты 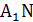 ;
; .
.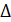 АВС, А(6;5), В(1;-3), С(-4;2).
АВС, А(6;5), В(1;-3), С(-4;2).
 , где В(1;-3), С(-4;2). Тогда
, где В(1;-3), С(-4;2). Тогда

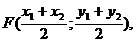 где В(1;-3), С(-4;2).
где В(1;-3), С(-4;2). 
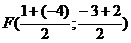 , F(-1,5;-0,5).
, F(-1,5;-0,5). ,
,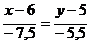 ,
, .
.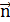 =
= 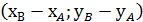
 ,
,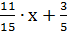 , k1 =
, k1 =  - угловой коэффициент медианы AF.
- угловой коэффициент медианы AF.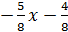 , k2=
, k2= 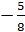 - угловой коэффициент высоты CE.
- угловой коэффициент высоты CE.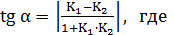 k1=
k1= 

 .
.


