Определение. Характеристическим уравнением линейного оператора f называется уравнение вида  , где λ –любое действительное число, А – матрица линейного оператора, Е – единичная матрица того же порядка.
, где λ –любое действительное число, А – матрица линейного оператора, Е – единичная матрица того же порядка.
Многочлен  называется характеристическим многочленом
называется характеристическим многочленом  матрицы А (линейного оператора f). В матричном виде характеристическое уравнение имеет следующий вид:
матрицы А (линейного оператора f). В матричном виде характеристическое уравнение имеет следующий вид:
 или
или
 .
.
Следовательно, приравнивая характеристический многочлен к нулю, получаем уравнение степени n, где в качестве неизвестного выступает λ, получаем значения его корней – характеристических чисел данной матрицы. Характеристические корни играют большую роль во многих разделах математики. Рассмотрим одно из применений характеристических корней – очень важный инструмент при исследовании линейных пространств, а также при решении многих прикладных задач линейной алгебры.
Набор всех корней характеристического уравнения называют спектром оператора f (каждый корень рассматривают с той кратностью, которую он имеет в характеристическом уравнении).
Пример. Найти характеристические корни матрицы  .
.
Составим матрицу
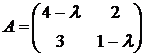
Приравнивая характеристический многочлен к нулю, получаем квадратное уравнение
 . Тогда корни уравнения равны
. Тогда корни уравнения равны  .
.
Определение. Пусть f линейный оператор пространства 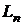 и
и  - некоторый ненулевой вектор, для которого справедливо равенство
- некоторый ненулевой вектор, для которого справедливо равенство

где  - действительное число. Тогда вектор
- действительное число. Тогда вектор 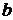 называют собственным вектором оператора и матрицы его задающего,
называют собственным вектором оператора и матрицы его задающего,  - собственным значением, или собственным числом преобразования. При этом говорят, что собственный вектор
- собственным значением, или собственным числом преобразования. При этом говорят, что собственный вектор 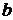 относится к собственному значению
относится к собственному значению  .
.
Собственные векторы играют большую роль, как в самой математике, так и в ее приложениях. Например, резонанс, при котором собственные частоты колебаний системы, совпадают с частой колебаний внешних сил. В математике собственные векторы полезны при решении систем дифференциальных уравнений.
Теорема. Если линейный оператор f в базисе  (первый базис) имеет матрицу А и в базисе
(первый базис) имеет матрицу А и в базисе 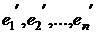 (второй базис) – матрицу В, то имеет место равенство:
(второй базис) – матрицу В, то имеет место равенство:  .
.
Следовательно, при переходе к новому базису характеристический многочлен линейного оператора не меняется.
◌ Если Т – матрица перехода от первого базиса ко второму, то  . Тогда преобразуем правую часть равенства
. Тогда преобразуем правую часть равенства 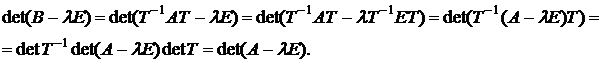 ●
●
Теорема. Для того чтобы число λ0 из поля Р было собственным значением вектора пространства Ln над Р необходимо и достаточно, чтобы число λ0 являлось характеристическим корнем оператора f.
Док-во. I. Необходимость. Пусть λ0 собственное значение оператора f, тогда в Ln существует собственный вектор 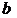 , такой, что
, такой, что  .
.
Пусть  – его координатная строка в некотором базисе, тогда
– его координатная строка в некотором базисе, тогда
 (1)
(1)
С другой стороны, т.к.  , где
, где  – матрица линейного оператора в заданном базисе, то
– матрица линейного оператора в заданном базисе, то
 (2)
(2)
Приравняв правые части (1) и (2) получим:
 (3)
(3)
Равенства (3) означают, что числовой вектор с координатами 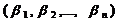 является решением следующей системы уравнений (4).
является решением следующей системы уравнений (4).
 (4)
(4)
Вектор 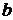 отличен от нулевого (т.к. он собственный), поэтому система (4) имеет ненулевое решение, следовательно ее определитель равен 0.
отличен от нулевого (т.к. он собственный), поэтому система (4) имеет ненулевое решение, следовательно ее определитель равен 0.
 (5)
(5)
а значит и транспонируемый определитель равен 0.
 (6)
(6)
Таким образом, λ0 – корень характеристического уравнения.
II. Достаточность. Пусть λ0 – характеристический корень оператора  в некотором базисе
в некотором базисе  . Докажем, что λ0 является собственным значением оператора A.
. Докажем, что λ0 является собственным значением оператора A.
Действительно, если λ0 – характеристический корень, то будет выполняться равенство (6), а следовательно, равенство (5), а это будет означать, что система (4) имеет ненулевые решения.
Выберем какое-нибудь ненулевое решение системы(4): числовой вектор  . Тогда выполняются равенства (3).
. Тогда выполняются равенства (3).
Рассмотрим вектор  , а для него будет выполняться равенство (2) и, в силу формулы
, а для него будет выполняться равенство (2) и, в силу формулы  , справедливо равенство (1), где
, справедливо равенство (1), где  – матрица оператора
– матрица оператора  в базисе В. Отсюда следует равенство
в базисе В. Отсюда следует равенство  , которое означает, что вектор
, которое означает, что вектор 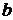 является собственным вектором оператора
является собственным вектором оператора  , которому соответствуют собственное значение λ0. Это и требовалось доказать. Теорема доказана.
, которому соответствуют собственное значение λ0. Это и требовалось доказать. Теорема доказана.
Замечание. Для того чтобы найти собственные значения оператора, надо составить и решить уравнение (5). Чтобы найти собственные векторы оператора нужно составить систему уравнений (4) и найти фундаментальный набор решений этой системы.
Для контроля за правильностью вычисления собственных значений (они могут быть совпадающие, комплексные) используются два факта:
1)  , где последняя сумма след матрицы – сумма диагональных элементов.
, где последняя сумма след матрицы – сумма диагональных элементов.
2)  .
.
Пример. Найти собственные значения и собственные векторы  .
.
 Приравнивая к нулю получаем
Приравнивая к нулю получаем  .
.
Найдем собственные векторы.
1)  .
.  ,
,  .
.
 .
.

Пусть  - свободная переменная, тогда
- свободная переменная, тогда  Получаем вектор
Получаем вектор  .
.
2)  .
.  ,
,  .
.
 .
.

Пусть  - свободная переменная, тогда
- свободная переменная, тогда
 Получаем вектор
Получаем вектор  .
.
3)  .
.  ,
,  .
.
 .
.

Пусть  - свободная переменная, тогда
- свободная переменная, тогда 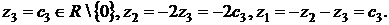 Получаем вектор
Получаем вектор  .
.
Упражнение. Сделать проверку для вектора  .
.
 .
.



 , где λ –любое действительное число, А – матрица линейного оператора, Е – единичная матрица того же порядка.
, где λ –любое действительное число, А – матрица линейного оператора, Е – единичная матрица того же порядка. матрицы А (линейного оператора f). В матричном виде характеристическое уравнение имеет следующий вид:
матрицы А (линейного оператора f). В матричном виде характеристическое уравнение имеет следующий вид: или
или .
. .
.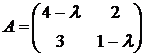
 . Тогда корни уравнения равны
. Тогда корни уравнения равны  .
.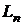 и
и  - некоторый ненулевой вектор, для которого справедливо равенство
- некоторый ненулевой вектор, для которого справедливо равенство
 - действительное число. Тогда вектор
- действительное число. Тогда вектор 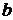 называют собственным вектором оператора и матрицы его задающего,
называют собственным вектором оператора и матрицы его задающего,  (первый базис) имеет матрицу А и в базисе
(первый базис) имеет матрицу А и в базисе 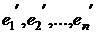 (второй базис) – матрицу В, то имеет место равенство:
(второй базис) – матрицу В, то имеет место равенство:  .
. . Тогда преобразуем правую часть равенства
. Тогда преобразуем правую часть равенства 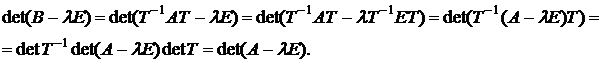 ●
●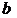 , такой, что
, такой, что  .
. – его координатная строка в некотором базисе, тогда
– его координатная строка в некотором базисе, тогда (1)
(1) , где
, где  – матрица линейного оператора в заданном базисе, то
– матрица линейного оператора в заданном базисе, то (2)
(2) (3)
(3)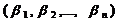 является решением следующей системы уравнений (4).
является решением следующей системы уравнений (4). (4)
(4) (5)
(5) (6)
(6) в некотором базисе
в некотором базисе  . Докажем, что λ0 является собственным значением оператора A.
. Докажем, что λ0 является собственным значением оператора A. . Тогда выполняются равенства (3).
. Тогда выполняются равенства (3). , а для него будет выполняться равенство (2) и, в силу формулы
, а для него будет выполняться равенство (2) и, в силу формулы  , справедливо равенство (1), где
, справедливо равенство (1), где  – матрица оператора
– матрица оператора  , где последняя сумма след матрицы – сумма диагональных элементов.
, где последняя сумма след матрицы – сумма диагональных элементов. .
. .
. Приравнивая к нулю получаем
Приравнивая к нулю получаем  .
. .
.  ,
,  .
. .
.
 - свободная переменная, тогда
- свободная переменная, тогда  Получаем вектор
Получаем вектор  .
. .
.  ,
,  .
. .
.
 - свободная переменная, тогда
- свободная переменная, тогда Получаем вектор
Получаем вектор  .
. .
.  ,
,  .
. .
.
 - свободная переменная, тогда
- свободная переменная, тогда 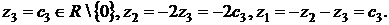 Получаем вектор
Получаем вектор  .
. .
. .
.


