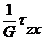Закон Гука для линейного напряженного состояния. Вспомним курс сопротивления материалов.
Пусть стержень растягивается вдоль своей оси х напряжениями sx=s.(рис.Р1)
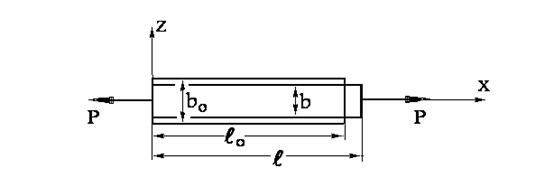
Рис. Р1
Относительное удлиннение eх = 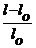 (продольная деформация) пропорционально напряжению s = sх:
(продольная деформация) пропорционально напряжению s = sх:
eх = 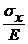 или sх = Еeх. (Р1)
или sх = Еeх. (Р1)
Коэффициент пропорциональности Е называют модулем упругости или модулем Юнга.
Относительные удлиннения в любом из перпендикулярных направлений ey = ez = 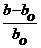 (поперечные деформации) тоже пропорциональны напряжениям, следовательно, пропорциональны деформации eх. Пишут так:
(поперечные деформации) тоже пропорциональны напряжениям, следовательно, пропорциональны деформации eх. Пишут так:
ey = ez = - m ex = 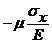 , (P2)
, (P2)
где m - коэффициент поперечной деформации или коэффициент Пуассона. Из (Р2) следует:
m = 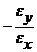
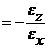 (Р2-а)
(Р2-а)
Коэффициент Пуассона - это взятое с обратным знаком отношение поперечной деформации к продольной при осевом растяжнии стержня. Знак минус в формуле (Р2) поставлен потому, что при растяжении стержня продольная деформация eх положительна (длина стержня увеличивается), а поперечные деформации ey = ez – отрицательны (поперечные размеры сокращаются). Коэффициент m в при такой постановке оказывается положительным.
Закон Гука для произвольного напряженного состояния в главных осях тензора напряжений. Теперь построим соотношения для произвольного напряженного состояния, заданного главными напряжениями. Пусть главные оси 1, 2, 3 совпадают с координатными осями x, y, z. (рис.P1).
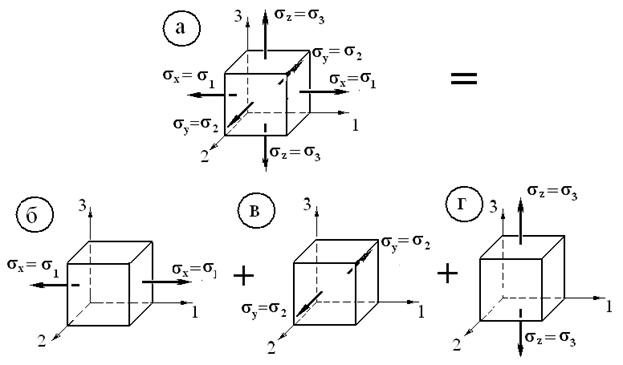
Рис.Р2.
Произвольное напряженное состояние, характеризуемое тремя главными напряжениями (а) может быть представлено как сумма трех состояний (б)+(в)+(г), каждое из которых является одноосным растяжением в направлении соответствующей оси. Относительные удлинения вдоль осей 1, 2, 3 в каждом из частных случаев б, в, г определятся по формулам (р1) и (р2).
- случай (б): e1 = 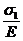 , e2 =
, e2 = 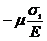 , e3 =
, e3 = 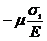 ,
,
- случай (в): e1 = 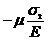 , e2 =
, e2 = 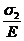 , e3 =
, e3 = 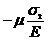 , (Р3)
, (Р3)
- случай (г): e1 = 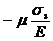 , e2 =
, e2 = 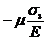 , e3 =
, e3 = 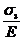 ,
,
В соответствии с принципом суперпозиции при одновременном действии напряжений s1, s2, и s3 каждая из компонент деформаций равна сумме ее значений при действии каждого напряжения в отдельности. Просуммировав (по столбцам) результаты (Р3), получим:
e1 = 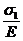
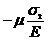
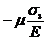 =
= 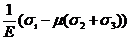 ,
,
e2 = 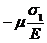 +
+ 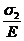
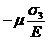 =
= 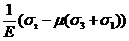 , (Р4)
, (Р4)
e3 = 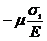
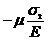 +
+ 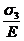 =
= 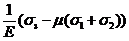 .
.
Из симметрии напряжений и свойств материала следует, что деформации сдвига между главными осями равны нулю, следовательно для изотропного материала главные оси тензоров напряжений и деформаций совпадают, эти тензоры соосны.
Закон Гука припроизвольном напряженном состоянии в произвольных координатны осях. Пусть произвольные оси x, y, z наклонены к главным осям 1, 2, 3 под углами, косинусы которых образуют матрицу (L):
(L) = 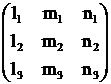 (P5)
(P5)
При повороте осей компоненты напряжений преобразуются по формулам (9-а) главы 1. Поскольку исходные оси 1, 2, 3 главные, эти формулы принимают вид:
sx = 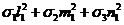
sy = 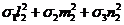 (Р6)
(Р6)
sz = 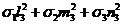 ,
,
txy = 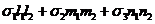
tyz =............
tzх =............
Компоненты тензора деформаций преобразуются по аналогичному закону:
ex = 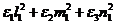
ey = 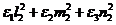 (Р7)
(Р7)
ez = 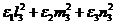 ,
,
1/2 g xy = 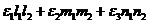
1/2 g yz =............
1/2 g zх =............
Задача состоит в том, чтобы выразить компоненты деформаций ex,ey,ez,gxy,gyz,gzx через напряжения sx,sy,sz,txy,tyz,tzx.
В первую формулу из (Р7) подставим значения главных деформаций из (Р4):
ex = 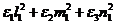 =
= 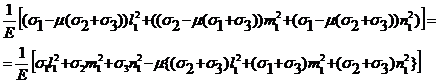
К множителю при m в фигурной скобке добавим ±s1l2 ± s2m2 ± s3n2, получим:
ex = 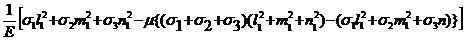
Учитывая, что
s1+s2+s3 = sx + sy + sz, (это первый инвариант тензора напряжений),
l12+m12+n12 = 1,
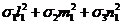 = sx (первая формула из (Р6)), получим:
= sx (первая формула из (Р6)), получим:
ex = 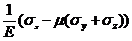 ,
,
Аналогично получаются формулы для двух других линейных деформаций ey и ez.
Теперь определим деформацию сдвига из четвертой формулы (Р7):
g xy =2(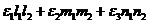 ) =
) = 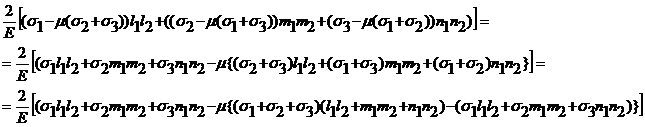
(К выражению в фигурной скобке добавлено ±s1l1l2 ± s2m1m2 ± s3n1n2). Учитывая, что из (Р7-4) следует
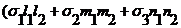 ) = txy ,
) = txy ,
а из ортогональности новых координатных осей: 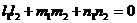 , получим:
, получим:
g xy 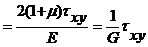 , (Р8)
, (Р8)
где G = 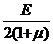 (Р9)
(Р9)
Упругая постоянная материала G называется модулем сдвига или модулем упругости при сдвиге. Модуль сдвига связывает деформацию сдвига g с касательным напряжением t,которое ее вызывает.
Аналогично получаются выражения для деформаций g yz и g zx. Полностью система уравнений закона Гука в произвольных осях имеет вид:
ex = 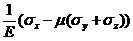 g xy =
g xy = 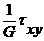
ey = 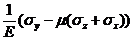 g yz =
g yz = 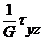 (P10)
(P10)
ez = 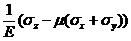 g zx =
g zx = 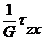
Дальше не закончено.




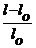 (продольная деформация) пропорционально напряжению s = sх:
(продольная деформация) пропорционально напряжению s = sх: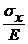 или sх = Еeх. (Р1)
или sх = Еeх. (Р1)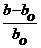 (поперечные деформации) тоже пропорциональны напряжениям, следовательно, пропорциональны деформации eх. Пишут так:
(поперечные деформации) тоже пропорциональны напряжениям, следовательно, пропорциональны деформации eх. Пишут так: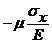 , (P2)
, (P2)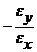
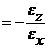 (Р2-а)
(Р2-а)
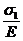 , e2 =
, e2 = 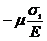 , e3 =
, e3 = 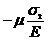 , e2 =
, e2 = 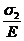 , e3 =
, e3 = 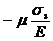 , e2 =
, e2 = 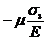 , e3 =
, e3 = 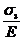 ,
,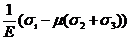 ,
,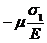 +
+ 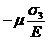 =
= 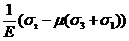 , (Р4)
, (Р4)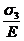 =
= 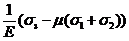 .
.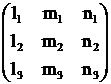 (P5)
(P5)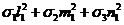
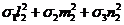 (Р6)
(Р6)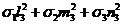 ,
,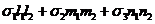
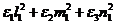
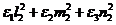 (Р7)
(Р7)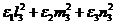 ,
,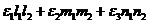
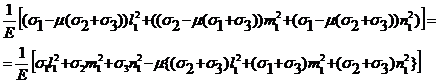
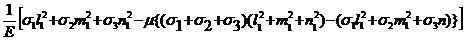
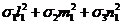 = sx (первая формула из (Р6)), получим:
= sx (первая формула из (Р6)), получим: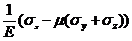 ,
,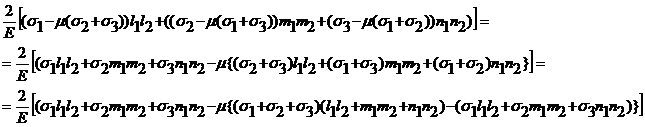
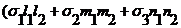 ) = txy ,
) = txy ,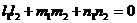 , получим:
, получим: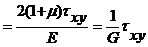 , (Р8)
, (Р8)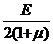 (Р9)
(Р9)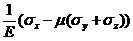 g xy =
g xy = 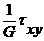
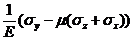 g yz =
g yz = 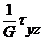 (P10)
(P10)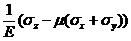 g zx =
g zx =