Навигация:

Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Новые материалы

Топ:

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...

Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...

История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...

Интересное:

Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...

Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...

Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...

Дисциплины:

Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция

Тема 4. Предел последовательности и предел функции. Непрерывность функции.

2017-10-16

399

0.00 из 5.00 0 оценок

Заказать работу

⇐ ПредыдущаяСтр 4 из 8Следующая ⇒

Содержание программы

4.1. Понятие предела последовательности и его свойства.

4.2. Неопределенности. Вычисление пределов последовательностей. Формула числа е.

4.3. предел функции в точке и на бесконечности(по Гейне), его свойства.

4.4. Вычисление пределов.

4.5. Понятие бесконечно малой и бесконечно большой функции, их свойства.

4.6. Неопределенности. Первый и второй замечательные пределы.

4.7. Непрерывность функции в точке.

Содержание темы

Число а называют пределом числовой последовательности {x_n}, если .

Обозначается .

Число А называется пределом функции f(x) в точке х₀, если такое, что . Обозначается .

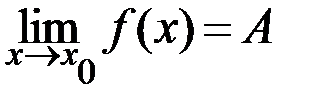Свойства пределов:

Если существуют конечные пределы и , то

1) ,

2) ,

3) , если ,

4) ,

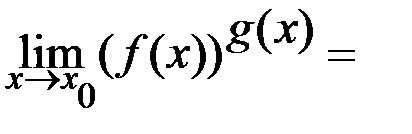
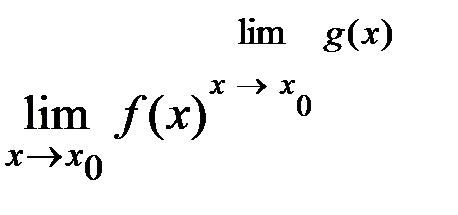5) .

Более сложными случаями нахождения предела являются такие, когда подстановка предельного значения аргумента в выражение для f(x) приводит к одной из неопределенностей∞⁰, ∞ - ∞, 0 ^. ∞, ∞/∞, 0/0, 0⁰, 1^∞.

Чтобы раскрыть неопределенность вида 0/0, необходимо провести преобразования функции и сократить числитель и знаменатель дроби на выражение (х – х₀).

Чтобы раскрыть неопределенность вида ∞/∞, необходимо числитель и знаменатель дроби сократить на аргумент в большей степени.

Чтобы раскрыть неопределенности вида ∞⁰, 0 ^. ∞ и др., необходимо первоначально привести их к виду 0/0 или ∞/∞.

Первый замечательный предел

И второй замечательный предел .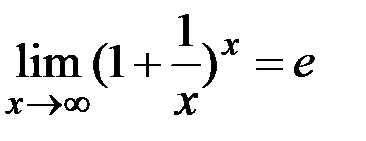

Пример 4.1. Вычислить пределы:

а) , б) ,

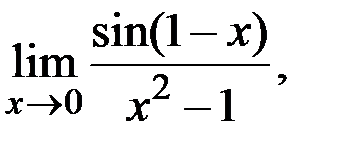в) , г) д) .

Решение

а)

б)

в)

г)

д) =

Функция непрерывна в точке , если предельное значение этой функции в точке существует и равно частному значению , или:

1) функция определена в точке и некоторой ее окрестности;

2) существует ;

3) .

Точка , в которой функция не обладает свойством непрерывности, называется точкой разрыва функции .

Точка называется точкой устранимого разрыва, если существует, но функция не определена в точке или нарушено условие .

Точка называется точкой разрыва I рода, если не существует, но при этом существуют конечные односторонние пределы и 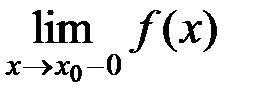, неравные друг другу.

Точка называется точкой разрыва II рода, если хотя бы один из односторонних пределов , не существует или равен бесконечности.

Пример 4.2. Исследовать функцию на непрерывность, определить характер разрыва.

Функция не определена в точках , уже нарушено первое условие непрерывности, следовательно, в этих точках функция испытывает разрыв.

Для выяснения характера разрыва нужно вычислить односторонние пределы в точках .

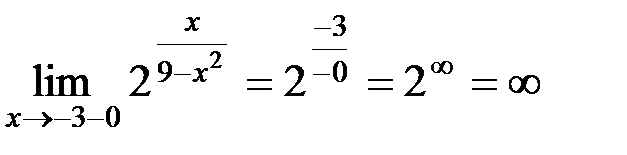Так как левый предел в точке равен бесконечности, то в ней разрыв II рода.

;

Так как правый предел в точке равен бесконечности, то в ней разрыв II рода.

Пример 4.3. .

Функция неопределена в нуле, следовательно, – точка разрыва.

Так как и , то это устранимый разрыв, функцию можно в нуле доопределить “по непрерывности”, положив равной единице.

Контрольные вопросы

1. Что называют пределом числовой последовательности?

2. Что называют пределом функции в точке?

2. Какие вы знаете правила вычисления пределов?

3. Что представляют собой первый и второй замечательные пределы?

4. Как раскрывают неопределенность вида 0/0?

5. Как раскрывают неопределенность вида ∞/∞?

6. Как раскрывают неопределенности вида ∞⁰, 0 ^. ∞ и др.?

7. Что называется пределом последовательности?

8. Что называется пределом функции в точке?

9. Что называется левосторонним пределом функции в данной точке?

10. Что называется правосторонним пределом функции в данной точке?

11. Какая функция называется непрерывной в точка?

12. Какая функция называется непрерывной на отрезке?

13. Какая функция называется непрерывной?

14. Что называется точкой разрыва функции?

15. Какие бывают точки разрыва функции?

Тема 5. Дифференциальное исчисление функции одной и многих переменных

Содержание программы

5.1. Приращение аргумента и приращение функции. Понятие производной функции.

5.2. Физический и геометрический смысл производной.

5.3. Основные правила дифференцирования. Таблица производных. Нахождение производных по таблице и правилам дифференцирования.

5.4. Производная сложной функции.

5.5. Уравнение касательной е графику функции.

5.6. Нахождение наименьшего и наибольшего значений функции на отрезке.

5.7. Правило Лопиталя.

5.8. Дифференциал первого порядка.

5.9. Производные высших порядков.

5.10. Монотонность и локальный экстремум функции.

5.11. Выпуклость, вогнутость и перегиб графика функции.

5.12. Понятие функции многих переменных.

5.13.Частные производные первого порядка функции многих переменных и дифференциал функции многих переменных.

5.14. Частные производные высших порядков.

Содержание темы

Производной функции у = f(x) в точке х₀ называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т. е.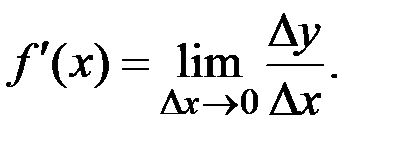

Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке.

Операция нахождения производной называется дифференцированием.

Правила дифференцирования:

Пусть С – постоянная, а u (x) и v (x) - дифференцируемые функции.

1. С ^/ = 0.

2. (u + v) ^/ = u ^/ + v^/.

3. (uv) ^/ = u ^/ v+ v^/u.

4. (Cu) ^/ = Cu^/.

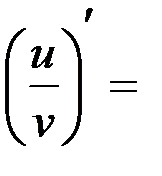
5. , v 0.

Геометрический смысл производной: производная функции f (х) в точке х₀ равна угловому коэффициенту касательной, проведенной к графику функции в его точке с абсциссой х₀.

Физический смысл производной: мгновенная скорость прямолинейного движения материальной точки в любой момент времени t есть производная от пути s по времени t:

v(t) = s ^/(t) =

Если у = g(и), и = и(х) – функции своих аргументов, причем область определения функции g (u) содержит область значений u (x), то каждому х области определения функции u соответствует у такое, что у = g(и), и=и(х). Эта функция, определяемая соответствием

у = g(u(x)),

называется функцией от функции или сложной функцией (композицией функций).

Производная сложной функции у = g(u(x)). Если функция и = и(х) дифференцируема в точке х, а функция у = g(и) дифференцируема в соответствующей точке и = и(х), то сложная функция у = g(u(x)) дифференцируема в точке х и ее производная у ^/(x)= g^/(x) ^.u ^/ (x).

Таблица производных

1. (хⁿ) ^/ = nx^n-1, 8. (log_a x)^/ = 1/xlnx,

2. (a^x) ^/ = a^xln a, 9. (ln x)^/ = 1/x,

3. (e^x) ^/ = e^x, 10. (arctg x)^/ = 1/ (1 + x²),

4. (sin x)^/ = cos x, 11. (arcctg x)^/ = - 1/ (1 + x²),

5. (cos x)^/ = - sin x, 12. (arcsin x)^/ = 1/ ,

6. (tg x)^/ = 1/cos² x,

7. (ctg x)^/ = - 1/sin² x, 13. (arccos x)^/ = - 1/ .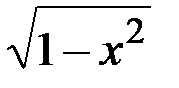

Пример 5.1. Найти производную функции:

а) у = е^х (х² – 2х + 7),

б) у = sin (2x + 3),

в) у = (х³ + 3х² – 1)¹³.

Решение

а) найдем производную данной функции, воспользовавшись формулой производной произведения двух функций:

у ^/ = (е^х)^/ (х² – 2х + 7) + е^х (х² – 2х + 7)^/ = е^х (х² – 2х + 7) + е^х (2х – 2) = е^х (х² – 2х + + 7 + 2х – 2) = е^х (х² + 5),

б) найдем производную сложной функции:

у ^/ = (sin (2x + 3))^/ = cos (2x + 3) ^. (2x+ 3)^/ = 2cos (2x + 3),

в) у^/ = ((х³ + 3х² – 1)¹³)^/= 13(х³ + 3х² – 1)¹² (х³ + 3х² – 1)^/ = 13(х³ + 3х²– 1)¹²(3х²+ 6х)

Функция у = f (x) на некотором интервале задана неявно уравнением F (x; y) = 0, если для всех х из этого интервала

F (x, f(x)) = 0.

Для нахождения производной функции, заданной неявно, следует тождество F (x, f(x)) = 0 продифференцировать по х, рассматривая левую часть как сложную функцию от х, а затем полученное уравнение разрешить относительно f ^/(x).

Пример 5.2. Найти производную функции у = f (x), заданной неявно

уравнением x² – 2x²y² + 5x + y – 5 = 0.

Решение Дифференцируя по х обе части тождества, получим

2х – (4ху²+ 2х²2уу^/) + 5 + y^/ = 0,

2х – 4ху²- 4х²уу^/ + 5 + y^/ = 0,

y^/ (1 – 4x²y) = 4xy² – 2x – 5,

.

Уравнение касательной к кривой в точке имеет вид:

, где -производная при .

Нормалью к кривой называется прямая, перпендикулярная касательной и проходящая через точку касания.

⇐ Предыдущая 1 2 345 6 7 8 Следующая ⇒
Поделиться с друзьями:

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...