

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Интересное:
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Метод Фурье или метод разделения переменных, широко используемый при решении ряда задач математической физики, состоит в следующем. Искомая функция, зависящая от нескольких переменных, ищется в виде произведения функций, каждая из которых зависит лишь от одной переменной. После подстановки этого произведения в исходное уравнение получается несколько обыкновенных дифференциальных уравнений, часть из которых вместе с краевыми условиями исходной задачи являются краевыми задачами, называемыми задачами Штурма- Лиувилля. Искомое решение представляется рядом по произведениям собственных функций задач Штурма- Лиувилля. Приведем с х е м у э т о г о м е т о д а для простейших уравнений гиперболического и параболического типов – волнового уравнения и уравнения теплопроводности.
Рассмотрим однородные уравнения

| (2.78) |
 , ,
| (2.79) |
для которых граничные условия имеют вид
 . .
| (2.80) |
а начальные условия таковы

| (2.81) |
для (2.78)

| (2.82) |
для (2.79).
Процесс решения разбивается на два этапа: I – нахождение частных решений; II – нахождение общего решения и удовлетворение начальным условиям.
I. Ищутся всевозможные частные решения (2.78) в виде
 . .
| (2.83) |
В результате подстановки функции такого вида в уравнение (2.78) получаем
 или
или  .
.
РЕШЕНИЕ УРАВНЕНИЯ КОЛЕБАНИЙ СТРУНЫ МЕТОДОМ ХАРАКТЕРИСТИК (МЕТОДОМ ДАЛАМБЕРА)
Одним из широко используемых способов решения уравнений колебаний струны является метод характеристик, называемый методом Даламбера. В основе его лежит тот факт, что с помощью замены 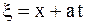 ,
, 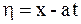 уравнение
уравнение
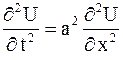
| (2.73) |
преобразуется в уравнение 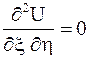 , которое имеет общее решение
, которое имеет общее решение
|
|
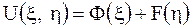 ,
,
где 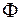 и
и 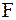 - произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функций
- произвольные дважды дифференцируемые функции (см. пример 2.40). Для определения функций 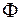 и
и 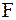 , т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным
, т.е. для определения закона колебаний струны, требуется использовать начальные условия, а для некоторых задач и граничные. Если вернуться к старым переменным 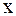 и
и 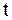 , то общее решение примет вид
, то общее решение примет вид
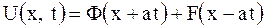 .
.
Здесь 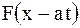 характеризует прямую волну (кривая
характеризует прямую волну (кривая 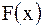 смещается вправо со скоростью
смещается вправо со скоростью 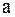 ), а
), а 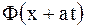 - обратную волну (кривая
- обратную волну (кривая 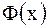 смещается влево со скоростью
смещается влево со скоростью 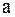 ).
).
Если рассматривается задача Коши для бесконечной струны 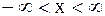 , то по заданным начальным условиям
, то по заданным начальным условиям
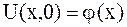 , , 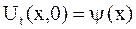
| (2.74) |
определяются функции 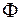 и
и 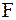 , и искомое решение имеет вид
, и искомое решение имеет вид
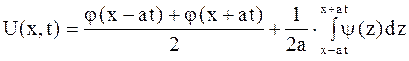 . .
| (2.75) |
Формула (2.75) называется формулой Даламбера. Эта формула доказывает единственность решения задачи Коши.
В частности, когда начальная скорость равна нулю (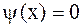 ), то
), то
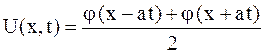 ,
,
откуда легко вычислить отклонение струны от положения равновесия для любой из ее точек; оно равно сумме левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией 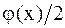 , равной половине начального отклонения.
, равной половине начального отклонения.
В случае полубесконечной струны, кроме начальных условий (2.74), заданных при 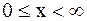 , необходимо добавить еще граничное условие (конец предполагается в точке
, необходимо добавить еще граничное условие (конец предполагается в точке 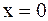 )
)
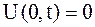
| (2.76) |
для закрепленной в точке 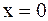 струны,
струны,
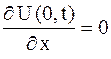
| (2.77) |
для свободного конца в точке 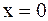 ,
,
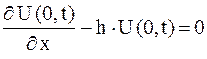 .
.
для упругого закрепления в точке 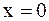 .
.
В случае однородных граничных условий (2.76) или (2.77) решение задачи о колебании полубесконечной струны сводится к решению задачи о колебании бесконечной струны путем продолжения начальных условий на всю ось нечетным образом для условия (2.76), т.е. полагают 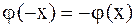 ,
, 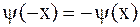 , и четным образом для условия (2.77), т.е.
, и четным образом для условия (2.77), т.е. 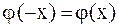 ,
, 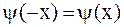 .
.
Примеры решения задач
ПРИМЕР 2.43. Найти форму достаточно длинной струны, определяемой уравнением 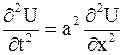 , в момент времени
, в момент времени 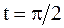 ,
, 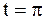 , если заданы начальные смещения и скорости:
, если заданы начальные смещения и скорости:
а) 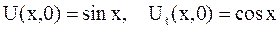 ;
;
б) 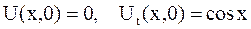 ;
;
в) 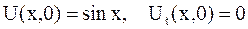 .
.
Решение. По постановке вопроса надо найти решение 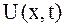 задачи Коши (2.73), (2.74) в области:
задачи Коши (2.73), (2.74) в области: 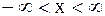 ,
, 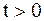 . Оно определяется формулой Даламбера (2.75).
. Оно определяется формулой Даламбера (2.75).
Случай а). Полагая в формуле Даламбера  ,
, 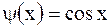 , найдем смещение
, найдем смещение 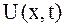 в любой точке и любой момент
в любой точке и любой момент 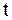 :
:
|
|
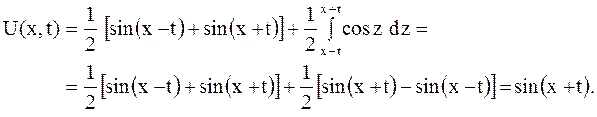
Откуда определяем форму кривой в указанные моменты времени:
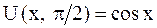 ,
, 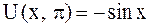 .
.
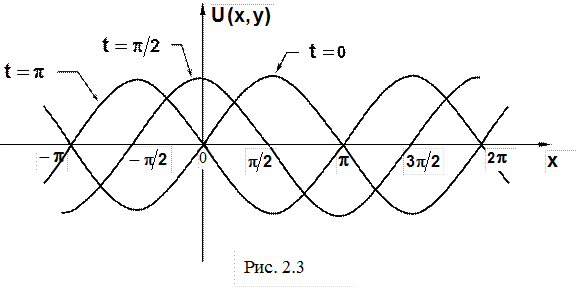
Кривые изображены на рис. 2.3.
Случай б) Начальные смещения струны равны нулю, т.к. 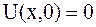 . При
. При 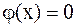 колебательный процесс будет описан по формуле
колебательный процесс будет описан по формуле
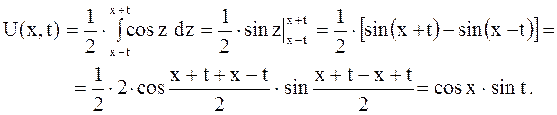
В момент времени 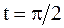 струна имеет форму косинусоиды:
струна имеет форму косинусоиды: 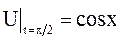 , а в момент
, а в момент 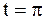 она совпадает с осью абсцисс:
она совпадает с осью абсцисс: 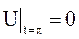 .
.
Случай в). По условию, начальные скорости равны нулю, значит, 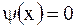 . Тогда имеем
. Тогда имеем
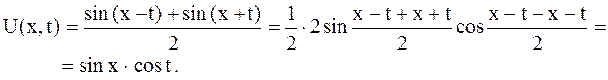
Форма струны в указанные моменты времени определяется уравнениями:
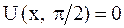 ,
, 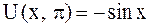 .
.
|
|
|

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!