Основы вариационного исчисления - II
Методические указания
и варианты заданий
для самостоятельной работы студентов
III курса специальностей КМ и ДПМ
Издательство
Пермского государственного технического университета
Составитель: В.В. Малыгина
УДК 517 (075.8)
О75
Рецензент:
канд. техн. наук, доцент кафедры ВММ И.Н. Бояршинова
Основы вариационного исчисления. Ч. II: метод. указания и варианты заданий для самостоятельной работы студентов III курса специальностей КМ и ДПМ / сост. В.В. Малыгина. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. – 58 с.
Данное методическое пособие является продолжением пособия «Основы вариационного исчисления – I», сохраняя его обозначения и терминологию, а также продолжая нумерацию формул, примеров и заданий. В часть II вошли разделы «Вариационные задачи на плоскости и в пространстве», «Вариационные задачи с подвижными границами» и «Задачи на условный экстремум».
УДК 517 (075.8)
© ГОУ ВПО
«Пермский государственный
технический университет», 2008
Вариационные задачи с подвижными границами
В предыдущих лекциях при исследовании функционала
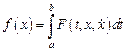
 предполагалось, что граничные точки
предполагалось, что граничные точки 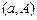 и
и 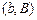 заданы. Подобное предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера задачу навигации.
заданы. Подобное предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера задачу навигации.
Задача навигации
В этой задаче рассматривается река ширины 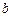 с прямыми параллельными берегами. Считая один берег реки совпадающим с осью
с прямыми параллельными берегами. Считая один берег реки совпадающим с осью 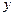 , введем скорость течения реки
, введем скорость течения реки 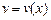 . Лодка с постоянной скоростью
. Лодка с постоянной скоростью
(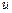 – величина скорости,
– величина скорости, 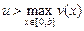 ), за кратчайшее время должна пересечь реку, отчалив из точки
), за кратчайшее время должна пересечь реку, отчалив из точки 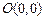 (рис.1).
(рис.1).
Обозначим через 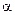 угол, который образует вектор скорости лодки с положительным направлением оси
угол, который образует вектор скорости лодки с положительным направлением оси 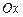 . Тогда реальная скорость движения лодки в момент времени
. Тогда реальная скорость движения лодки в момент времени 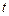 определяется равенствами
определяется равенствами
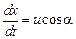 ,
, 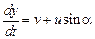 .
.
Отсюда
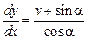 ,
,
что позволяет выразить 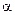 через
через 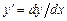 :
:
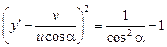 ,
,
откуда
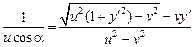 .
.
Для времени пересечения реки находим
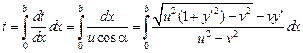 .
.
Последний интеграл должен быть минимизирован за счет выбора функции 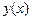 при условии
при условии 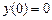 .
.
Как видим, в отличие от предыдущих задач, правый конец искомой кривой заранее не определен: он может оказаться на любой точке вертикальной прямой 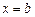 . Мы приходим, таким образом, к задаче со свободной (подвижной) границей. Найдем ее решение в общей постановке.
. Мы приходим, таким образом, к задаче со свободной (подвижной) границей. Найдем ее решение в общей постановке.
Решение задачи навигации
Вернемся к задаче навигации и найдем ее решение, используя полученный выше результат.
Итак, нам следует найти минимум функционала
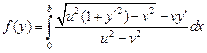
при условии 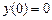 , а
, а 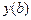 может принимать любое значение.
может принимать любое значение.
Согласно вышеприведенной схеме, решаем уравнение Эйлера. Так как подынтегральная функция
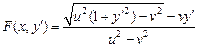
зависит только от 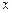 и
и 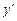 , то уравнение Эйлера допускает первый интеграл:
, то уравнение Эйлера допускает первый интеграл: 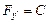 . С другой стороны, поскольку вторая граница экстремали перемещается по вертикальной прямой, для нее должно выполняться условие
. С другой стороны, поскольку вторая граница экстремали перемещается по вертикальной прямой, для нее должно выполняться условие 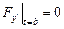 . Отсюда сразу следует, что вышеприведенный первый интеграл имеет вид:
. Отсюда сразу следует, что вышеприведенный первый интеграл имеет вид: 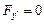 . Получаем дифференциальное уравнение первого порядка
. Получаем дифференциальное уравнение первого порядка
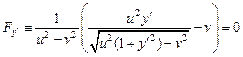 ,
,
для которого легко найти решение. Находя явное выражение для 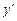 , получаем
, получаем 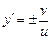 . Так как предполагается (см. рис. 1), что переправа осуществляется с левого берега на правый, то перед дробью следует выбрать знак плюс. Учитывая, что
. Так как предполагается (см. рис. 1), что переправа осуществляется с левого берега на правый, то перед дробью следует выбрать знак плюс. Учитывая, что 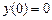 , получаем окончательно:
, получаем окончательно:
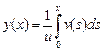 .
.
В частности, если 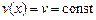 , то искомый маршрут наибыстрейшей переправы реализуется на прямой
, то искомый маршрут наибыстрейшей переправы реализуется на прямой 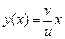 .
.
Изопериметрическая задача
Интересный класс задач на условный экстремум образуют так называемые изопериметрические задачи. Классической задачей такого вида (давшей название всему классу задач) является задача Дидоны: найти замкнутую кривую, ограничивающую наибольшую площадь при заданном периметре. При этом и минимизируемый функционал (площадь) и ограничение (периметр) задаются определенными интегралами.
Рассмотрим задачу в общей постановке. Пусть на кривых 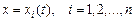 с фиксированными концами
с фиксированными концами 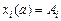 ,
, 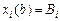 функционал
функционал
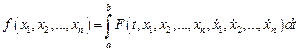
достигает своего минимального (максимального) значения, причем интегралы
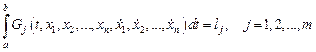
обладают заранее заданными значениями 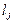 . Функции
. Функции 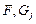 и
и 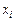 считаются дважды непрерывно дифференцируемыми.
считаются дважды непрерывно дифференцируемыми.
На первый взгляд кажется, что интегральные ограничения существенно усложняют задачу, и к изопериметрической задаче неприменимы методы предыдущего раздела. Однако оказалось, что изопериметрическую задачу остроумным приемом можно свести к задаче на условный экстремум с функциональными условиями связи.
Обозначим
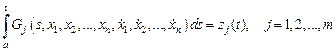 .
.
Тогда
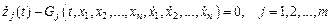
– новые условия связи, уже дифференциально-функционального вида, а изопериметрические условия превращаются в граничные условия:
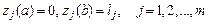 .
.
Таким образом, задача свелась к задаче на условный экстремум, для которой выше был приведен алгоритм решения. Следуя ему, составляем вспомогательную функцию
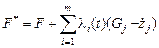 ,
,
для которой система уравнений Эйлера имеет вид:
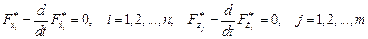 .
.
Но так как 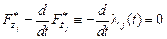 , то
, то 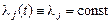 , а тогда
, а тогда
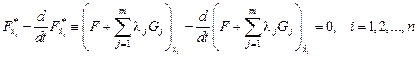 .
.
Следовательно, для изопериметрической задачи в качестве функции Лагранжа можно взять функцию
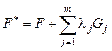
с постоянными множителями 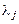 . Далее для функции
. Далее для функции 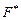 , как и ранее, выписывается и решается система уравнений Эйлера, а для определения произвольных постоянных и параметров
, как и ранее, выписывается и решается система уравнений Эйлера, а для определения произвольных постоянных и параметров 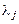 используются граничные и изопериметрические условия. То обстоятельство, что множители
используются граничные и изопериметрические условия. То обстоятельство, что множители 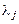 оказываются постоянными, безусловно, упрощает решение задачи.
оказываются постоянными, безусловно, упрощает решение задачи.
Пример 9. Найти экстремум функционала
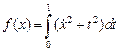
на классе функций, удовлетворяющих граничным условиям 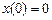 ,
, 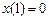 и дополнительному условию
и дополнительному условию 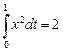 .
.
Решение. Поставленная задача, очевидно, относится к классу изопериметрических задач, поэтому, согласно приведенной выше схеме, запишем вспомогательную функцию 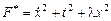 , для которой составим уравнение Эйлера:
, для которой составим уравнение Эйлера: 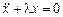 . Так как знак
. Так как знак 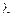 неизвестен, решение уравнения Эйлера следует провести для каждого из трех случаев:
неизвестен, решение уравнения Эйлера следует провести для каждого из трех случаев: 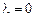 ,
, 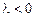 и
и 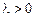 .
.
- Пусть
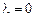 , тогда решение уравнения Эйлера имеет вид
, тогда решение уравнения Эйлера имеет вид
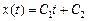 .
.
Подставляя граничные условия, находим 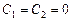 , то есть
, то есть 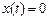 . Но это решение не удовлетворяет условию
. Но это решение не удовлетворяет условию 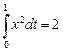 , следовательно, при
, следовательно, при 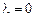 решений у задачи нет.
решений у задачи нет.
- Пусть
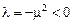 , тогда решение уравнения Эйлера имеет вид
, тогда решение уравнения Эйлера имеет вид
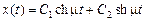 ,
,
из граничных условий снова получаем 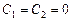 , а
, а 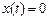 , то есть при
, то есть при 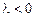 задача также не имеет решений.
задача также не имеет решений.
- Пусть
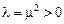 , тогда решение уравнения Эйлера имеет вид
, тогда решение уравнения Эйлера имеет вид
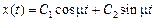 ,
,
подставляя граничные условия, находим 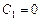 ,
, 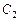 – любое число,
– любое число, 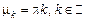 . Следовательно,
. Следовательно, 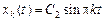 , где
, где 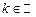 . Определим
. Определим 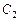 через изопериметрическое условие:
через изопериметрическое условие:
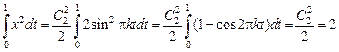 .
.
Получаем 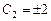 , то есть
, то есть 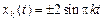 . Так как
. Так как 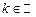 , то можно оставить перед функцией один знак. Окончательно получаем, что данная вариационная задача имеет бесконечное множество решений вида:
, то можно оставить перед функцией один знак. Окончательно получаем, что данная вариационная задача имеет бесконечное множество решений вида:
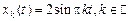 .
.
Примеры решения некоторых вариационных задач
В качестве иллюстрации построенной теории решим три классические задачи: задачу Дидоны, задачу о брахистохроне и задачу о минимальной поверхности вращения. Каждую из этих задач сначала переформулируем в вариационных терминах, то есть поставим ее как задачу отыскания минимума функционала с заданными граничными условиями, а затем решим ее разработанными выше методами вариационного исчисления.
Задача Дидоны
Вспомним задачу, о которой говорилось в начале курса: мы оставили Дидону в тот момент, когда ей нужно было ограничить шнуром фиксированной длины максимальную площадь. Мы уже освоили вариационное исчисление настолько хорошо, что можем помочь Дидоне.
Рассмотрим множество функций 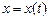 , определенных на отрезке
, определенных на отрезке 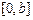 , таких, что
, таких, что 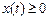 при всех
при всех 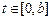 , а
, а 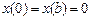 (рис. 3). Вместе с отрезком
(рис. 3). Вместе с отрезком 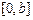 график каждой функции
график каждой функции 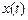 ограничивает площадь, задаваемую функционалом
ограничивает площадь, задаваемую функционалом

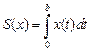 .
.
Потребуем дополнительно, чтобы кривые 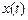 имели фиксированную длину, то есть постоянное значение сохранял функционал вида:
имели фиксированную длину, то есть постоянное значение сохранял функционал вида:
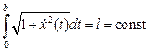 .
.
Мы получаем, таким образом, изопериметрическую задачу, для которой нам уже известны методы решения.
Выстраиваем вспомогательную функцию 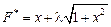 и записываем для нее уравнение Эйлера. Функция
и записываем для нее уравнение Эйлера. Функция 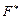 не зависит от переменной
не зависит от переменной 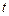 , следовательно, уравнение Эйлера допускает первый интеграл
, следовательно, уравнение Эйлера допускает первый интеграл
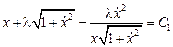 ,
,
представляющий собой дифференциальное уравнение первого порядка, не разрешенное относительно производной. Разрешая его относительно 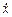 , получаем уравнение в разделяющихся переменных, интегральными кривыми которого являются окружности:
, получаем уравнение в разделяющихся переменных, интегральными кривыми которого являются окружности:
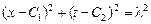 .
.
Учитывая граничные условия, находим, что 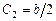 , а
, а 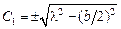 . Не нарушая общности, можем считать, что интересующая нас дуга окружности не больше ее половины, тогда центр окружности лежит ниже оси
. Не нарушая общности, можем считать, что интересующая нас дуга окружности не больше ее половины, тогда центр окружности лежит ниже оси 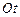 , и
, и 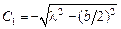 . Для определения параметра
. Для определения параметра 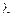 , то есть радиуса искомой окружности, используем условие постоянства периметра.
, то есть радиуса искомой окружности, используем условие постоянства периметра.
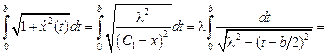
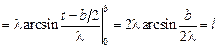 .
.
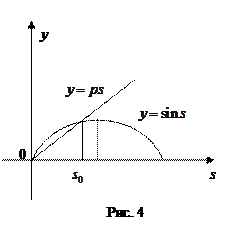 Уравнение
Уравнение 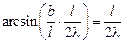 эквивалентно уравнению
эквивалентно уравнению 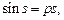 где
где 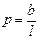 ,
, 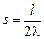 ,
, 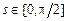 . Из геометрических соображений ясно, что задача содержательна лишь при условии
. Из геометрических соображений ясно, что задача содержательна лишь при условии 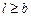 , следовательно,
, следовательно, 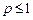 , а тогда уравнение
, а тогда уравнение 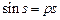 всегда имеет на отрезке
всегда имеет на отрезке 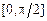 единственный корень
единственный корень 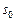 (рис. 4).
(рис. 4).
Отсюда находим радиус искомой окружности 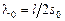 и координаты ее центра:
и координаты ее центра: 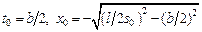 .
.
Задача о брахистохроне
Предположим, что точки 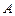 и
и 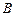 лежат в плоскости
лежат в плоскости 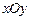 с осью
с осью 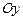 , направленной вниз (рис.5). Положим
, направленной вниз (рис.5). Положим 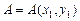 и
и 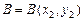 и пусть
и пусть 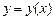 – уравнение дуги, соединяющей точки
– уравнение дуги, соединяющей точки 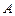 и
и 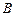 так, что
так, что 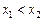 ,
, 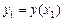 ,
, 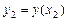 ,
, 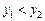 . Скорость движения вдоль кривой пусть равна
. Скорость движения вдоль кривой пусть равна 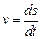 . Тогда время спуска равно
. Тогда время спуска равно

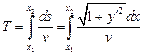 .
.
Чтобы найти скорость v как функцию координаты x, воспользуемся законом сохранения энергии:
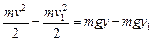 ,
,
где 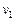 — начальная скорость движения частицы. Тогда
— начальная скорость движения частицы. Тогда
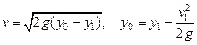 ,
,
и задача свелась к выбору функции 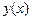 , для которой интеграл
, для которой интеграл
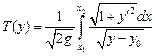
достигает наименьшего значения из всех возможных.
Так как функция 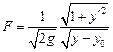 зависит только от
зависит только от 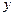 и
и 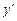 , то уравнение Эйлера допускает первый интеграл:
, то уравнение Эйлера допускает первый интеграл:
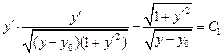 .
.
Разрешая это уравнение относительно 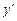 , находим
, находим
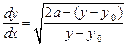 ,
,
где мы положили 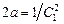 . Таким образом, мы получили дифференциальное уравнение первого порядка в разделяющихся переменных. Решая его, имеем:
. Таким образом, мы получили дифференциальное уравнение первого порядка в разделяющихся переменных. Решая его, имеем:
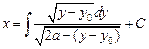 .
.
Для вычисления интеграла удобно воспользоваться заменой
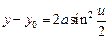 . Тогда
. Тогда 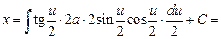
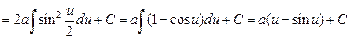 .
.
Мы пришли к решению в параметрической форме
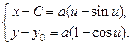
Это и есть кривая наибыстрейшего спуска, известная под названием циклоиды. Можно показать, что выбор постоянных 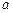 и
и 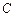 позволяет провести циклоиду через произвольные две заданные точки. Напомним, что величина
позволяет провести циклоиду через произвольные две заданные точки. Напомним, что величина 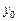 не является произвольной постоянной.
не является произвольной постоянной.
Список рекомендуемой литературы
1. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление / Л.Э. Эльсгольц. – М.: Эдиториал УРСС, 2000. – 319 с.
2. Романко В.К. Курс дифференциальных уравнений и вариационного исчисления / В.К. Романко. – М., СПб.: Физматлит, 2000. – 342 с.
3. Пантелеев А.В. Вариационное исчисление в примерах и задачах / А.В. Пантелеев. – М.: Изд-во МАИ, 2000. – 227 с.
Варианты заданий
Задание 5
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе.
1. 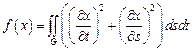 ,
,
 – сектор круга:
– сектор круга: 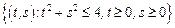 .
.
Граничные условия: 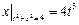 ,
, 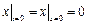 .
.
2. 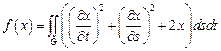 ,
,
 – кольцо:
– кольцо: 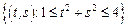 .
.
Граничные условия: 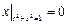 ,
, 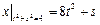 .
.
3. 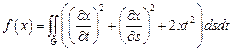 ,
,
 – круг:
– круг: 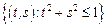 .
.
Граничные условия: 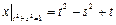 .
.
4. 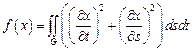 ,
,
 – квадрат:
– квадрат: 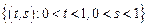 .
.
Граничные условия: 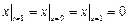 ,
, 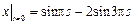 .
.
5. 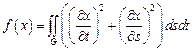 ,
,
 – сектор кольца:
– сектор кольца: 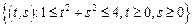 .
.
Граничные условия: 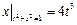 ,
, 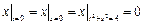 .
.
6. 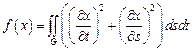 ,
,
 – сектор круга:
– сектор круга: 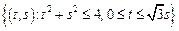 .
.
Граничные условия: 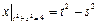 ,
, 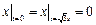 .
.
7. 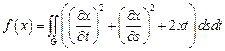 ,
,
 – кольцо:
– кольцо: 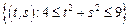 .
.
Граничные условия: 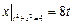 ,
, 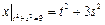 .
.
8. 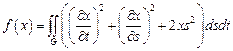 ,
,
 – круг:
– круг: 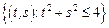 .
.
Граничные условия: 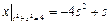 .
.
9. 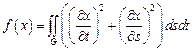 ,
,
 – квадрат:
– квадрат: 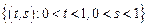 .
.
Граничные условия: 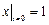 ,
, 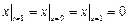 .
.
10. 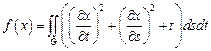 ,
,
 – сектор кольца:
– сектор кольца: 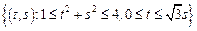 .
.
Граничные условия: 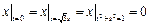 ,
, 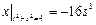 .
.
11. 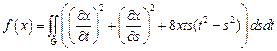 ,
,
 – сектор круга:
– сектор круга: 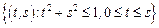 .
.
Граничные условия: 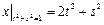 ,
, 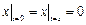 .
.
12. 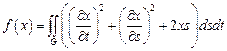 ,
,
 – кольцо:
– кольцо: 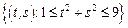 .
.
Граничные условия: 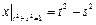 ,
, 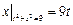 .
.
13. 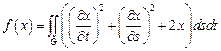 ,
,
 – круг:
– круг: 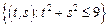 .
.
Граничные условия: 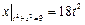 .
.
14. 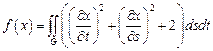 ,
,
 – квадрат:
– квадрат: 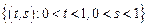 .
.
Граничные условия: 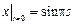 ,
, 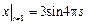 ,
, 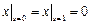 .
.
15. 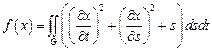 ,
,
 – сектор кольца:
– сектор кольца: 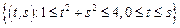 .
.
Граничные условия: 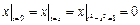 ,
, 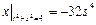 .
.
16. 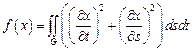 ,
,
 – сектор круга:
– сектор круга: 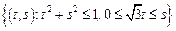 .
.
Граничные условия: 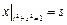 ,
, 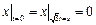 .
.
17. 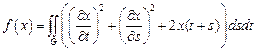 ,
,
 – кольцо:
– кольцо: 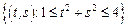 .
.
Граничные условия: 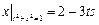 ,
, 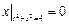 .
.
18. 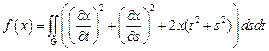 ,
,
 – круг:
– круг: 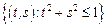 .
.
Граничные условия: 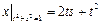 .
.
19. 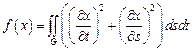 ,
,
 – квадрат:
– квадрат: 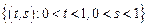 .
.
Граничные условия: 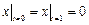 ,
, 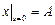 ,
, 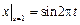 .
.
20. 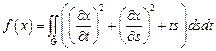 ,
,
 – сектор кольца:
– сектор кольца: 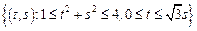 .
.
Граничные условия: 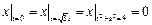 ,
, 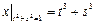 .
.
21. 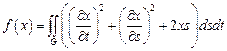 ,
,
 – сектор круга:
– сектор круга: 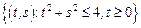 .
.
Граничные условия: 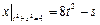 ,
, 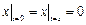 .
.
22. 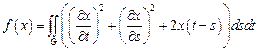 ,
,
 – кольцо:
– кольцо: 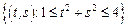 .
.
Граничные условия: 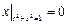 ,
, 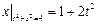 .
.
23. 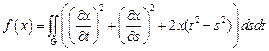 ,
,
 – круг:
– круг: 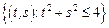 .
.
Граничные условия: 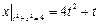 .
.
24. 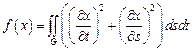 ,
,
 – квадрат:
– квадрат: 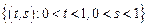 .
.
Граничные условия: 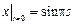 ,
, 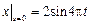 ,
, 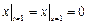 .
.
25. 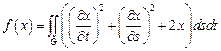 ,
,
 – сектор кольца:
– сектор кольца: 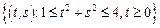 .
.
Граничные условия: 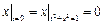 ,
, 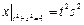 .
.
26. 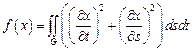 ,
,
 – сектор круга:
– сектор круга: 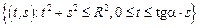 ,
, 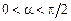 .
.
Граничные условия: 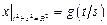 ,
,  , где
, где 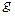 – произвольная непрерывная на отрезке
– произвольная непрерывная на отрезке 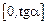 функция.
функция.
27. 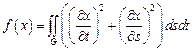 ,
,
 – кольцо:
– кольцо: 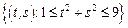 .
.
Граничные условия: 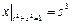 ,
, 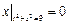 .
.
28. 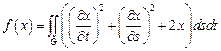 ,
,
 – круг:
– круг: 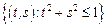 .
.
Граничные условия: 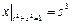 .
.
29. 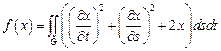 ,
,
 – квадрат:
– квадрат: 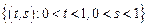 .
.
Граничные условия: 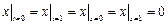 .
.
30. 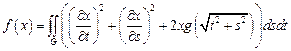 ,
,
 – сектор кольца:
– сектор кольца: 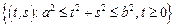 ,
, 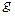 – непрерывная на отрезке
– непрерывная на отрезке 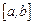 функция.
функция.
Граничные условия:  .
.
Задание 6
Найти экстремали следующих функционалов в указанных областях с заданными условиями на границе, используя для построения решения функции Бесселя и многочлены Лежандра.
1. 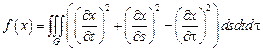 ,
,
 – прямой круговой цилиндр:
– прямой круговой цилиндр: 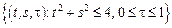 .
.
Граничные условия: 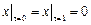 ,
, 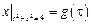 , где
, где 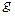 – непрерывная на отрезке
– непрерывная на отрезке 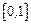 функция.
функция.
2. 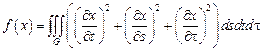 ,
,
 – прямой круговой цилиндр:
– прямой круговой цилиндр: 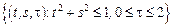 .
.
Граничные условия: 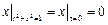 ,
, 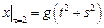 , где
, где 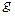 – непрерывная на отрезке
– непрерывная на отрезке 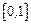 функция.
функция.
3. 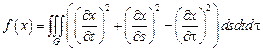 ,
,
 – прямой круговой цилиндр:
– прямой круговой цилиндр: 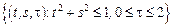 .
.
Граничные условия: 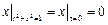 ,
, 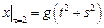 , где
, где 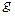 – непрерывная на отрезке
– непрерывная на отрезке 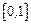 функция.
функция.
4. 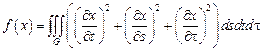 ,
,
 – шар:
– шар: 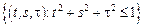 .
.
Граничные условия: 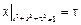 .
.
5. 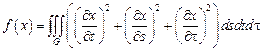 ,
,
 – шар:
– шар: 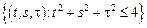 .
.
Граничные условия: 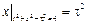 .
.
6. 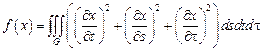 ,
,
 – шар:
– шар: 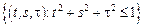 .
.
Граничные условия: 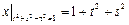 .
.
7. 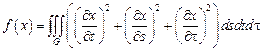 ,
,
 – шар:
– шар: 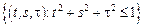 .
.
Граничные условия: 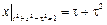 .
.
8. 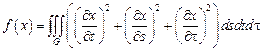 ,
,
 – шар:
– шар: 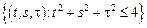 .
.
Граничные условия: 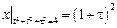 .
.
9. 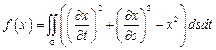 ,
,
 – круг:
– круг: 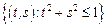 .
.
Граничные условия: 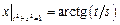 .
.
10. 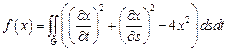 ,
,
 – сектор круга:
– сектор круга: 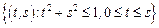 .
.
Граничные условия: 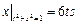 ,
, 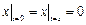 .
.
11. 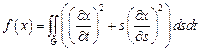 ,
,
 – квадрат:
– квадрат: 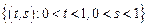 .
.
Граничные условия: 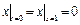 ,
, 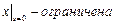 ,
, 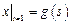 , где
, где 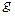 – непрерывная на отрезке
– непрерывная на отрезке 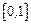 функция.
функция.
12. 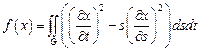 ,
,
 – квадрат:
– квадрат: 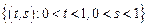 .
.
Граничные условия: 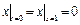 ,
, 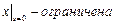 ,
, 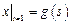 , где
, где 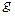 – непрерывная на отрезке
– непрерывная на отрезке 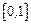 функция.
функция.
13. 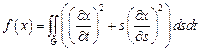 ,
,
 – прямоугольник:
– прямоугольник: 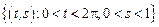 .
.
Граничные условия: 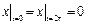 ,
, 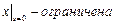 ,
, 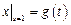 ,
,
где 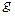 – непрерывная на отрезке
– непрерывная на отрезке 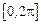 функция.
функция.
14. 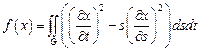 ,
,
 – прямоугольник:
– прямоугольник: 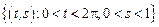 .
.
Граничные условия: 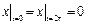 ,
, 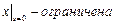 ,
, 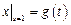 ,
,
где 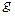 – непрерывная на отрезке
– непрерывная на отрезке 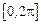 функция.
функция.
15. 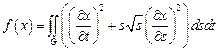 ,
,
 – квадрат:
– квадрат: 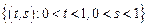 .
.
Граничные условия: 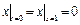 ,
, 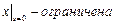 ,
, 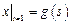 , где
, где 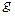 – непрерывная на отрезке
– непрерывная на отрезке 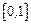 функция.
функция.
16. 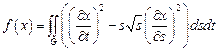 ,
,
 – квадрат:
– квадрат: 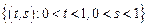 .
.
Граничные условия: 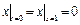 ,
, 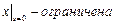 ,
, 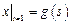 , где
, где 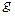 – непрерывная на отрезке
– непрерывная на отрезке 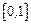 функция.
функция.
17. 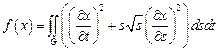 ,
,
 – прямоугольник:
– прямоугольник: 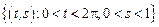 .
.
Граничные условия: 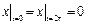 ,
, 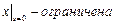 ,
, 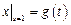 ,
,
где 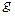 – непрерывная на отрезке
– непрерывная на отрезке 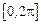 функция.
функция.
18. 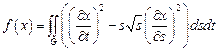 ,
,
 – прямоугольник:
– прямоугольник: 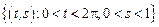 .
.
Граничные условия: 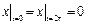 ,
, 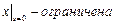 ,
, 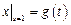 ,
,
где 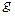 – непрерывная на отрезке
– непрерывная на отрезке 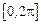 функция.
функция.
19. 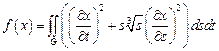 ,
,
 – квадрат:
– квадрат: 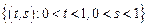 .
.
Граничные условия: 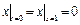 ,
, 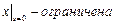 ,
, 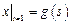 , где
, где 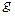 – непрерывная на отрезке
– непрерывная на отрезке 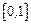 функция.
функция.
20. 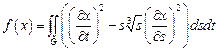 ,
,
 – квадрат:
– квадрат: 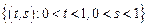 .
.
Граничные условия: 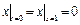 ,
, 
|
|
|



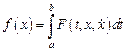
 предполагалось, что граничные точки
предполагалось, что граничные точки 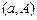 и
и 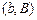 заданы. Подобное предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера задачу навигации.
заданы. Подобное предположение не всегда выполняется для многих интересных и практически важных вариационных задач. Рассмотрим в качестве примера задачу навигации.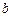 с прямыми параллельными берегами. Считая один берег реки совпадающим с осью
с прямыми параллельными берегами. Считая один берег реки совпадающим с осью 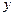 , введем скорость течения реки
, введем скорость течения реки 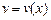 . Лодка с постоянной скоростью
. Лодка с постоянной скоростью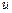 – величина скорости,
– величина скорости, 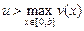 ), за кратчайшее время должна пересечь реку, отчалив из точки
), за кратчайшее время должна пересечь реку, отчалив из точки 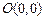 (рис.1).
(рис.1).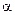 угол, который образует вектор скорости лодки с положительным направлением оси
угол, который образует вектор скорости лодки с положительным направлением оси 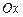 . Тогда реальная скорость движения лодки в момент времени
. Тогда реальная скорость движения лодки в момент времени 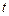 определяется равенствами
определяется равенствами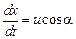 ,
, 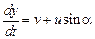 .
.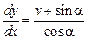 ,
,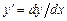 :
: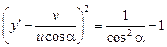 ,
,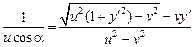 .
.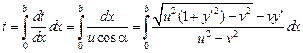 .
.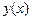 при условии
при условии 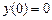 .
.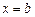 . Мы приходим, таким образом, к задаче со свободной (подвижной) границей. Найдем ее решение в общей постановке.
. Мы приходим, таким образом, к задаче со свободной (подвижной) границей. Найдем ее решение в общей постановке.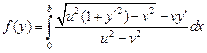
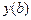 может принимать любое значение.
может принимать любое значение.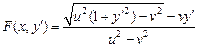
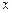 и
и 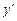 , то уравнение Эйлера допускает первый интеграл:
, то уравнение Эйлера допускает первый интеграл: 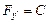 . С другой стороны, поскольку вторая граница экстремали перемещается по вертикальной прямой, для нее должно выполняться условие
. С другой стороны, поскольку вторая граница экстремали перемещается по вертикальной прямой, для нее должно выполняться условие 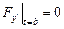 . Отсюда сразу следует, что вышеприведенный первый интеграл имеет вид:
. Отсюда сразу следует, что вышеприведенный первый интеграл имеет вид: 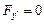 . Получаем дифференциальное уравнение первого порядка
. Получаем дифференциальное уравнение первого порядка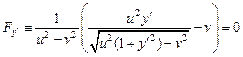 ,
,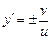 . Так как предполагается (см. рис. 1), что переправа осуществляется с левого берега на правый, то перед дробью следует выбрать знак плюс. Учитывая, что
. Так как предполагается (см. рис. 1), что переправа осуществляется с левого берега на правый, то перед дробью следует выбрать знак плюс. Учитывая, что 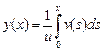 .
.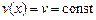 , то искомый маршрут наибыстрейшей переправы реализуется на прямой
, то искомый маршрут наибыстрейшей переправы реализуется на прямой 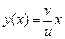 .
.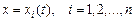 с фиксированными концами
с фиксированными концами 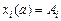 ,
, 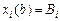 функционал
функционал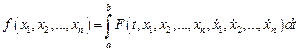
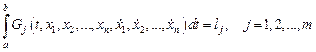
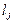 . Функции
. Функции 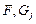 и
и 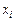 считаются дважды непрерывно дифференцируемыми.
считаются дважды непрерывно дифференцируемыми.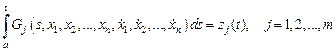 .
.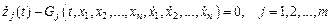
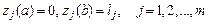 .
.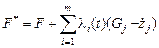 ,
,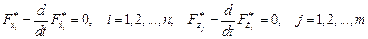 .
.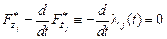 , то
, то 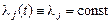 , а тогда
, а тогда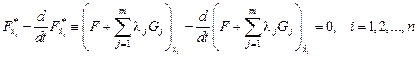 .
.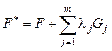
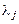 . Далее для функции
. Далее для функции 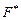 , как и ранее, выписывается и решается система уравнений Эйлера, а для определения произвольных постоянных и параметров
, как и ранее, выписывается и решается система уравнений Эйлера, а для определения произвольных постоянных и параметров 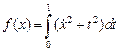
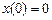 ,
, 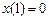 и дополнительному условию
и дополнительному условию 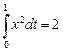 .
.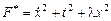 , для которой составим уравнение Эйлера:
, для которой составим уравнение Эйлера: 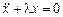 . Так как знак
. Так как знак 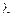 неизвестен, решение уравнения Эйлера следует провести для каждого из трех случаев:
неизвестен, решение уравнения Эйлера следует провести для каждого из трех случаев: 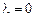 ,
, 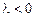 и
и 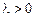 .
.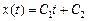 .
.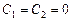 , то есть
, то есть 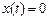 . Но это решение не удовлетворяет условию
. Но это решение не удовлетворяет условию 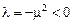 , тогда решение уравнения Эйлера имеет вид
, тогда решение уравнения Эйлера имеет вид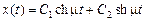 ,
,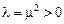 , тогда решение уравнения Эйлера имеет вид
, тогда решение уравнения Эйлера имеет вид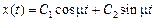 ,
,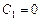 ,
, 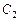 – любое число,
– любое число, 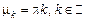 . Следовательно,
. Следовательно, 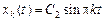 , где
, где 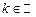 . Определим
. Определим 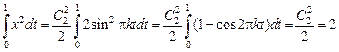 .
.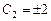 , то есть
, то есть 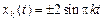 . Так как
. Так как 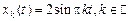 .
.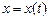 , определенных на отрезке
, определенных на отрезке 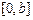 , таких, что
, таких, что 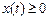 при всех
при всех 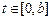 , а
, а 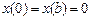 (рис. 3). Вместе с отрезком
(рис. 3). Вместе с отрезком 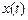 ограничивает площадь, задаваемую функционалом
ограничивает площадь, задаваемую функционалом
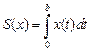 .
.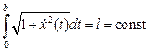 .
.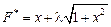 и записываем для нее уравнение Эйлера. Функция
и записываем для нее уравнение Эйлера. Функция 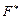 не зависит от переменной
не зависит от переменной 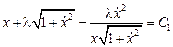 ,
,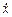 , получаем уравнение в разделяющихся переменных, интегральными кривыми которого являются окружности:
, получаем уравнение в разделяющихся переменных, интегральными кривыми которого являются окружности: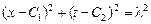 .
.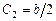 , а
, а 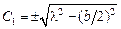 . Не нарушая общности, можем считать, что интересующая нас дуга окружности не больше ее половины, тогда центр окружности лежит ниже оси
. Не нарушая общности, можем считать, что интересующая нас дуга окружности не больше ее половины, тогда центр окружности лежит ниже оси 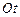 , и
, и 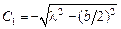 . Для определения параметра
. Для определения параметра 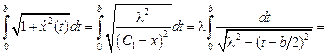
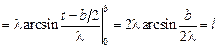 .
.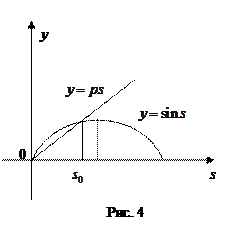 Уравнение
Уравнение 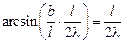 эквивалентно уравнению
эквивалентно уравнению 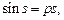 где
где 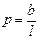 ,
, 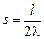 ,
, 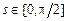 . Из геометрических соображений ясно, что задача содержательна лишь при условии
. Из геометрических соображений ясно, что задача содержательна лишь при условии 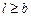 , следовательно,
, следовательно, 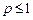 , а тогда уравнение
, а тогда уравнение 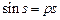 всегда имеет на отрезке
всегда имеет на отрезке 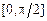 единственный корень
единственный корень 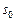 (рис. 4).
(рис. 4).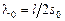 и координаты ее центра:
и координаты ее центра: 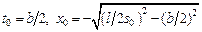 .
.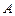 и
и 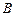 лежат в плоскости
лежат в плоскости 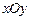 с осью
с осью 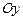 , направленной вниз (рис.5). Положим
, направленной вниз (рис.5). Положим 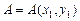 и
и 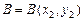 и пусть
и пусть 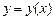 – уравнение дуги, соединяющей точки
– уравнение дуги, соединяющей точки 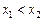 ,
, 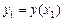 ,
, 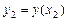 ,
, 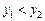 . Скорость движения вдоль кривой пусть равна
. Скорость движения вдоль кривой пусть равна 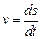 . Тогда время спуска равно
. Тогда время спуска равно
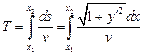 .
.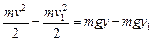 ,
,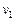 — начальная скорость движения частицы. Тогда
— начальная скорость движения частицы. Тогда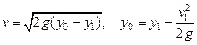 ,
,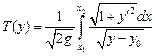
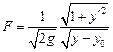 зависит только от
зависит только от 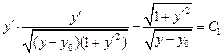 .
.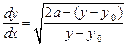 ,
,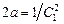 . Таким образом, мы получили дифференциальное уравнение первого порядка в разделяющихся переменных. Решая его, имеем:
. Таким образом, мы получили дифференциальное уравнение первого порядка в разделяющихся переменных. Решая его, имеем: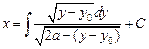 .
.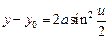 . Тогда
. Тогда 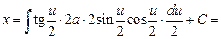
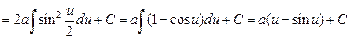 .
.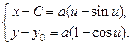
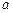 и
и 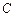 позволяет провести циклоиду через произвольные две заданные точки. Напомним, что величина
позволяет провести циклоиду через произвольные две заданные точки. Напомним, что величина 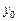 не является произвольной постоянной.
не является произвольной постоянной.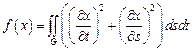 ,
, – сектор круга:
– сектор круга: 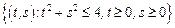 .
.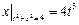 ,
, 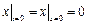 .
.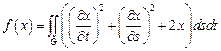 ,
,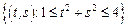 .
.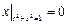 ,
, 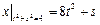 .
.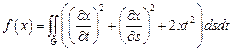 ,
,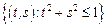 .
.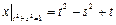 .
.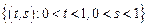 .
.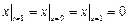 ,
, 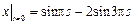 .
.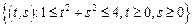 .
.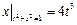 ,
, 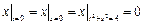 .
.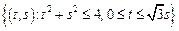 .
.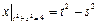 ,
, 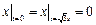 .
.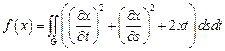 ,
,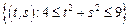 .
.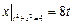 ,
, 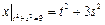 .
.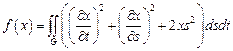 ,
,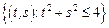 .
.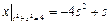 .
.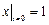 ,
, 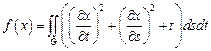 ,
,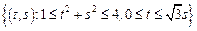 .
.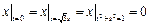 ,
, 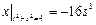 .
.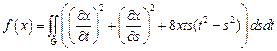 ,
,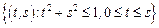 .
.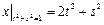 ,
, 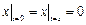 .
.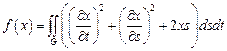 ,
,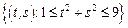 .
.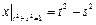 ,
, 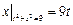 .
.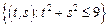 .
.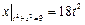 .
.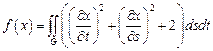 ,
,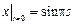 ,
, 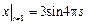 ,
, 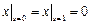 .
.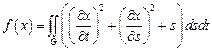 ,
,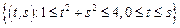 .
.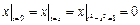 ,
, 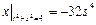 .
.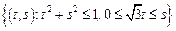 .
.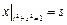 ,
, 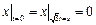 .
.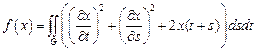 ,
,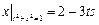 ,
, 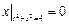 .
.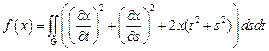 ,
,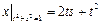 .
.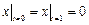 ,
, 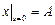 ,
, 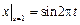 .
.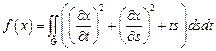 ,
,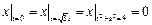 ,
, 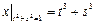 .
.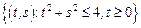 .
.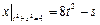 ,
, 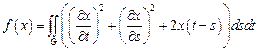 ,
,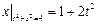 .
.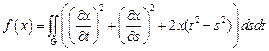 ,
,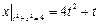 .
.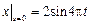 ,
, 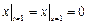 .
.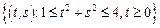 .
.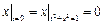 ,
, 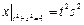 .
.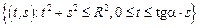 ,
, 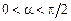 .
.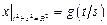 ,
,  , где
, где 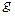 – произвольная непрерывная на отрезке
– произвольная непрерывная на отрезке 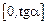 функция.
функция.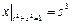 ,
, 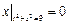 .
.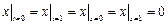 .
.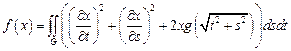 ,
,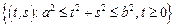 ,
, 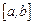 функция.
функция. .
.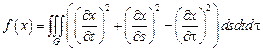 ,
,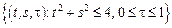 .
.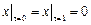 ,
, 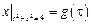 , где
, где 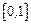 функция.
функция.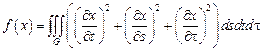 ,
,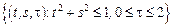 .
.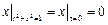 ,
, 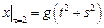 , где
, где 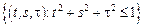 .
.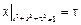 .
.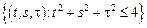 .
.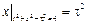 .
.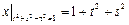 .
.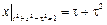 .
.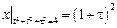 .
.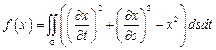 ,
,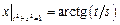 .
.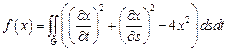 ,
,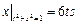 ,
, 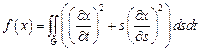 ,
,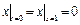 ,
, 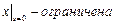 ,
, 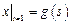 , где
, где  ,
, .
. ,
,  ,
,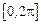 функция.
функция.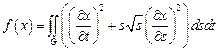 ,
,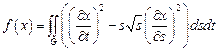 ,
,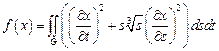 ,
,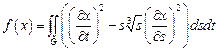 ,
,

