Как и Фильтр Калмана, метод наименьших квадратов может быть применен к линеаризованным моделям измерений. Пусть исходная нелинейная модель измерений имеет вид:
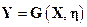 .
.
Тогда в результате линеаризации этой модели формально получим:
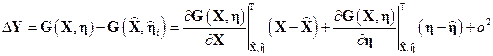 .
.
Откуда, полагая 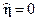 и вводя обозначения:
и вводя обозначения:
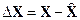 ;
; 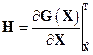 ;
; 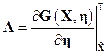 ,
,
получим результирующее соотношение:
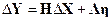 .
.
Отсюда соотношение для построения оценки фазового вектора методом наименьших квадратов примет окончательный вид:
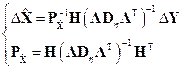
Построение матрицы Коши
В задачах построения оценок методами статистической обработки измерений часто встречается задача построения матрицы Коши. Эта матрица связывает фазовые векторы системы, отнесенные к разным моментам времени, в собственном движении.
Ограничимся в настоящем разделе рассмотрением вопросов, связанных с построением матрицы Коши для модели эволюции, записанной в виде системы обыкновенных дифференциальных уравнений (линейных или нелинейных).
Для линейной системы имеем:
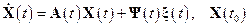 .
.
Тогда дифференциальное уравнение для матрицы Коши примет вид:
 .
.
Интегрируя его на интервале времени от 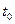 до
до  , с единичной матрицей соответствующей размерности в качестве начальных условий, получим матрицу Коши, связывающую фазовые векторы, отнесенные к моментам времени
, с единичной матрицей соответствующей размерности в качестве начальных условий, получим матрицу Коши, связывающую фазовые векторы, отнесенные к моментам времени 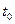 и
и  :
:
 .
.
В случае, когда модель эволюции фазового вектора представлена нелинейной системой дифференциальных уравнений общего вида:
 ,
,
матрица Коши может быть построена с использованием приведенных выше соотношений для линеаризованной системы:
 ,
,
где использованы следующие обозначения для матриц пропорциональности, построенных в окрестности опорной траектории 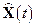 ,
,  :
:
 ;
;  .
.
Моделирование измерений
Проблема возникает в случае, когда, например, оценивая потенциально достижимую точность метода в некоторой задаче, Вы не располагаете какими-либо результатами измерениями. В этом случае результаты измерений требуется смоделировать. Особенность моделирования результатов измерений состоит в том, что модели движения и измерений, используемые для этой цели могут не совпадать с теми моделями, которые Вы будете использовать в ходе построения оценок с использованием того или иного метода фильтрации.
Более того, рекомендуется, чтобы модели, используемые для построения результатов измерений, были максимально точными, наилучшим образом приближенными к физическим процессам и закономерностям, наблюдающимся в природе.
В качестве начальных условий для моделирования эволюции фазового вектора динамической системы должны использоваться истинные значения координат этого вектора. Кроме этого места истинные значения координат фазового вектора системы не должны использоваться более нигде[7].
Численные методы
Специальные функции



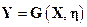 .
.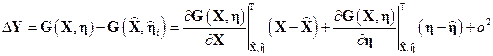 .
.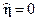 и вводя обозначения:
и вводя обозначения: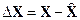 ;
; 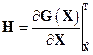 ;
; 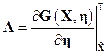 ,
,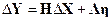 .
.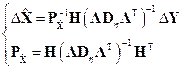
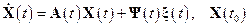 .
. .
.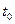 до
до  , с единичной матрицей соответствующей размерности в качестве начальных условий, получим матрицу Коши, связывающую фазовые векторы, отнесенные к моментам времени
, с единичной матрицей соответствующей размерности в качестве начальных условий, получим матрицу Коши, связывающую фазовые векторы, отнесенные к моментам времени  .
. ,
, ,
,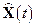 ,
,  :
: ;
;  .
.


