Рассмотрим пять классов булевых функций, которые называются замечательными классами, так как функции, принадлежащие к этим классам, обладают следующими свойствами: любая булева функция, полученная с помощью операций суперпозиции и подстановки из функций одного класса, обязательно будет принадлежать к тому же классу.
Напомним, что подстановкой называется замена одних аргументов функции другими или изменение порядка записи аргументов; суперпозицией называется подстановка в функцию вместо ее аргументов других функций.
Класс линейных функций от n аргументов (Ln).
В соответствии с теоремой Жегалкина любая булева функция представлена в виде полинома.
Булева функция называется линейной, если она может быть представлена полиномом первой степени, т.е. записана в виде
f(x1 x2 … xn)= α0  α1 x1
α1 x1  α2 x2
α2 x2  …
…  αn xn,
αn xn,
где α0, α1, …, αn – коэффициенты, равные 0 или 1.
Число различных линейных функций n переменных равно числу различных наборов вида <α0 α1 … αn > и равно 2n+1.
Пример. n=2. Класс L2 состоит из 8 функций:
f0(xy)=0; f3(xy)=x; f5(xy)=y;
f6(xy)= 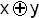 ; f9(xy)=1
; f9(xy)=1  x
x  y;
y;
f10(xy)=1  y; f12(xy)=1
y; f12(xy)=1  x; f15(xy)=1.
x; f15(xy)=1.
Отметим, что переключательные функции одного аргумента все линейны:
L1: f0(x)=0, f1(x)=x, f2(x)=1  x, f3(x)=1.
x, f3(x)=1.
Теорема. При суперпозиции линейных функций и при подстановке в эти функции других переменных получаются линейные переключательные функции и только они.
Дано f1(x1 x2 … xn)= α0  α1 x1
α1 x1  …
…  αn xn;
αn xn;
φ1(y1 y2 … 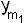 )= b10
)= b10  b11 y1
b11 y1  …
… 
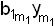 ;
;
φ2(y1 y2 … 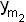 )= b20
)= b20  b21 y1
b21 y1  …
… 
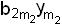 ;
;
....................
φn(y1 y2 … 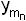 )= bn0
)= bn0  bn1 y1
bn1 y1  …
… 
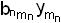 ,
,
Подставим φi вместо xi функции f1, получим выражение f2, в котором постоянные коэффициенты умножаются на линейные функции. Приведя подобные члены, получим представление функции f2 в виде линейного полинома.
Пример. f1(x1 x2 x3)=1  x1
x1  x2
x2  x3;
x3;
x1=φ1(y1 y2 y3 y4)= y1  y3
y3  y4;
y4;
x2=φ2(y1 y2)= 1  y1
y1  y2;
y2;
x3=φ3(y1 y2 y3 y4)= 1  y1
y1  y2
y2  y3
y3  y4;
y4;
f2(y1 y2 y3 y4)= 1  φ1(y1 y2 y3 y4)
φ1(y1 y2 y3 y4)  φ2(y1 y2)
φ2(y1 y2)  φ3(y1 y2 y3 y4)=
φ3(y1 y2 y3 y4)=
=1  y1
y1  y3
y3  y4
y4  1
1  y1
y1  y2
y2  1
1  y1
y1  y2
y2  y3
y3  y4=1
y4=1  y1.
y1.
При любых подстановках xi функция остается линейной.
Из линейных функций нельзя получить нелинейную, а наоборот можно.
Класс функций, сохраняющих нуль ( К0 ).
Если функция на нулевом наборе аргументов <00…0> равна нулю, то говорят, что функция сохраняет нуль:
f(000…0)=0.
При фиксированном n число таких функций составляет половину всех булевых функций n аргументов, т.е. 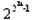 .
.
Пример. n=2. В класс К0входят следующие функции:
f0(xy), f1(xy), f2(xy), f3(xy), f4(xy), f5(xy), f6(xy), f7(xy).
При суперпозиции переключательных функций, сохраняющих нуль, и при подстановке в эти функции других переменных получаются переключательные функции, сохраняющие нуль и только они.
Пусть имеем
f1(x1 x2 … xn), φ1(y1 y2 … 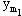 ), …, φn(y1 y2 …
), …, φn(y1 y2 … 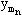 ).
).
Все эти функции сохраняют нуль на нулевом наборе. Подставив вместо xi функции φi, получим новую функцию
f2(y1 y2 … 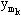 )= f1(φ1,φ2, …,φn ).
)= f1(φ1,φ2, …,φn ).
Найдем значение f2 на нулевом наборе:
f2 (00 …0)= f1 (000 …0)=0.
Так как на нулевом наборе все аргументы равны нулю, то любая подстановка этих аргументов не изменит значение функции.
6) Класс функций, сохраняющих единицу (К1).
Если булева функция на единичном наборе <111…1> аргументов равна единице, то говорят, что эта функция сохраняет единицу:
f(111…1)=1.
Так как на одном наборе <11..1> значение функции зафиксировано, то остается 2n-1 независимых наборов, т.е. число функций, сохраняющих единицу, равно половине от всех функций n переменных, т.е. 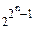 .
.
Пример. n=2. Класс К1содержит:
f1(xy), f3(xy), f5(xy), f7(xy), f9(xy), f11(xy), f13(xy), f15(xy).
Теорема. При суперпозиции переключательных функций, сохраняющих 1, и при подстановке в эти функции других переменных получаются функции, сохраняющие 1, и только они.



 α1 x1
α1 x1 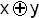 ; f9(xy)=1
; f9(xy)=1 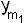 )= b10
)= b10 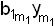 ;
;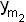 )= b20
)= b20 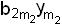 ;
;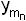 )= bn0
)= bn0 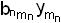 ,
,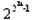 .
.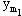 ), …, φn(y1 y2 …
), …, φn(y1 y2 … 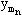 ).
).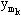 )= f1(φ1,φ2, …,φn ).
)= f1(φ1,φ2, …,φn ).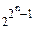 .
.


